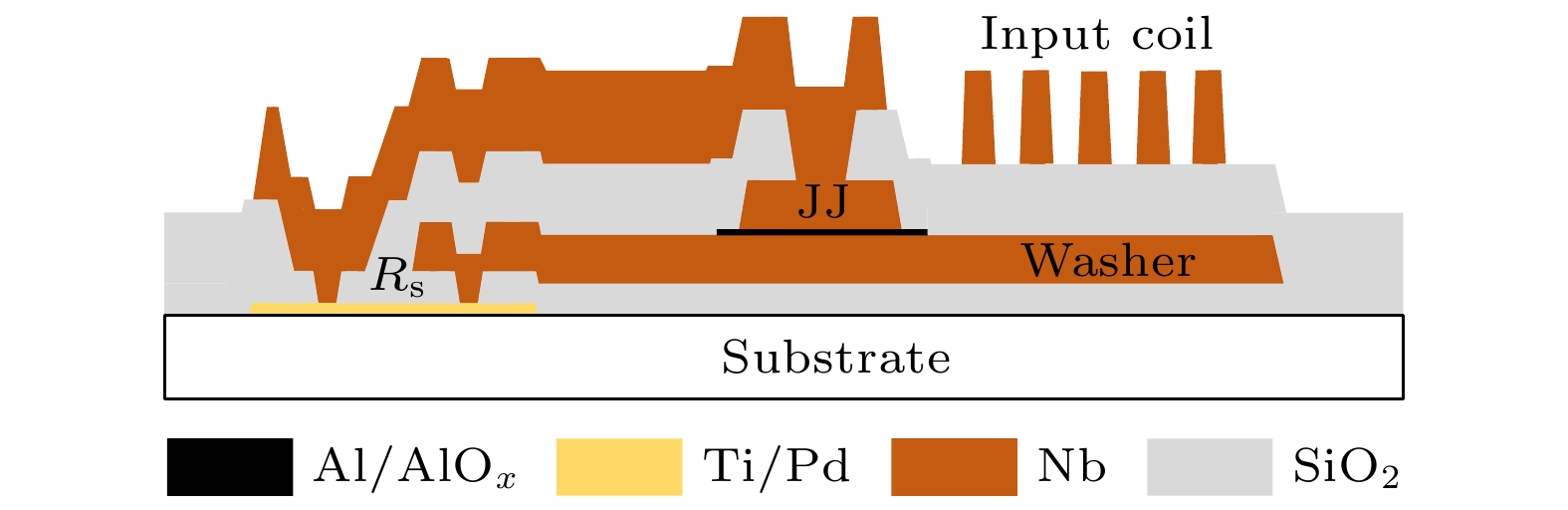
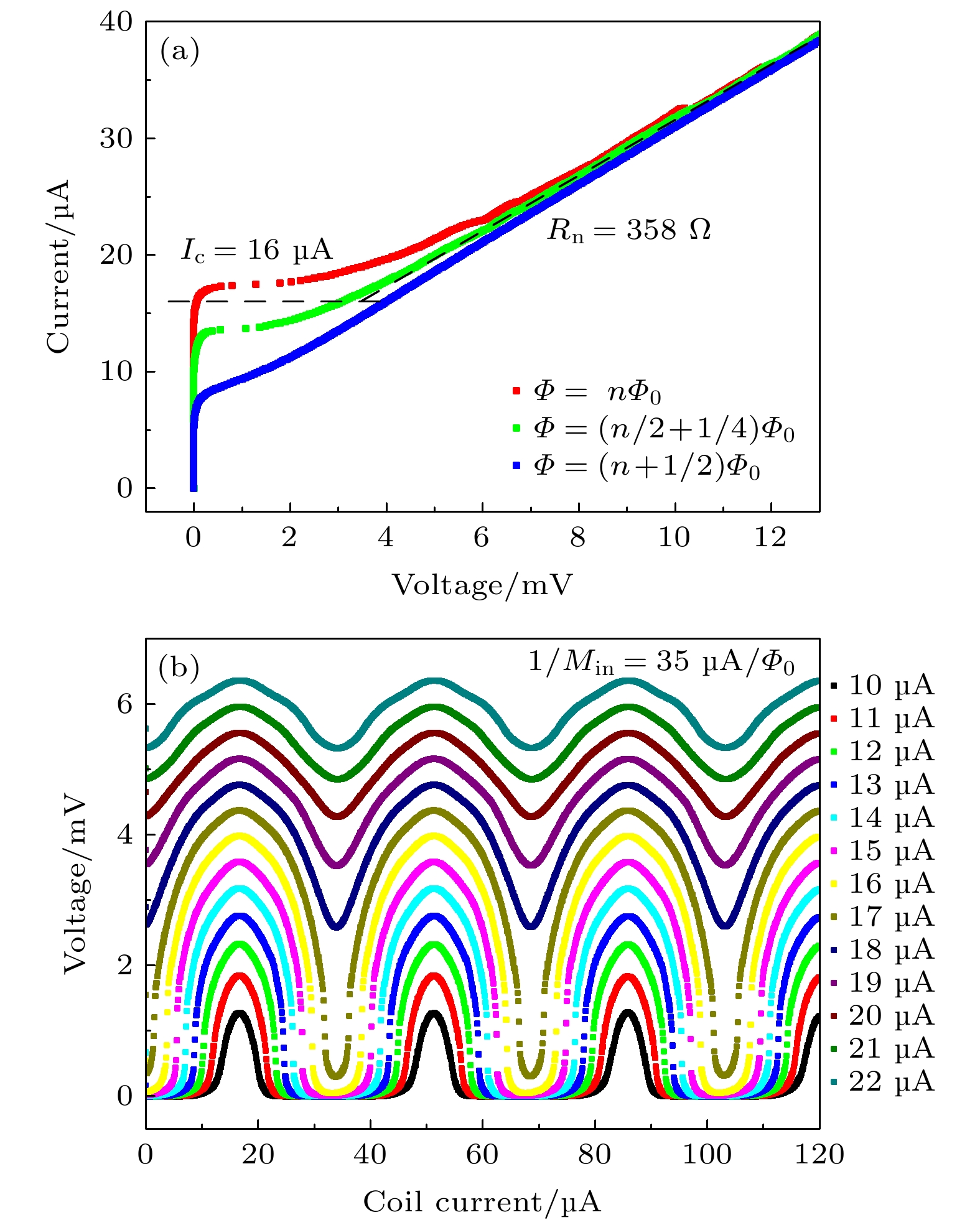
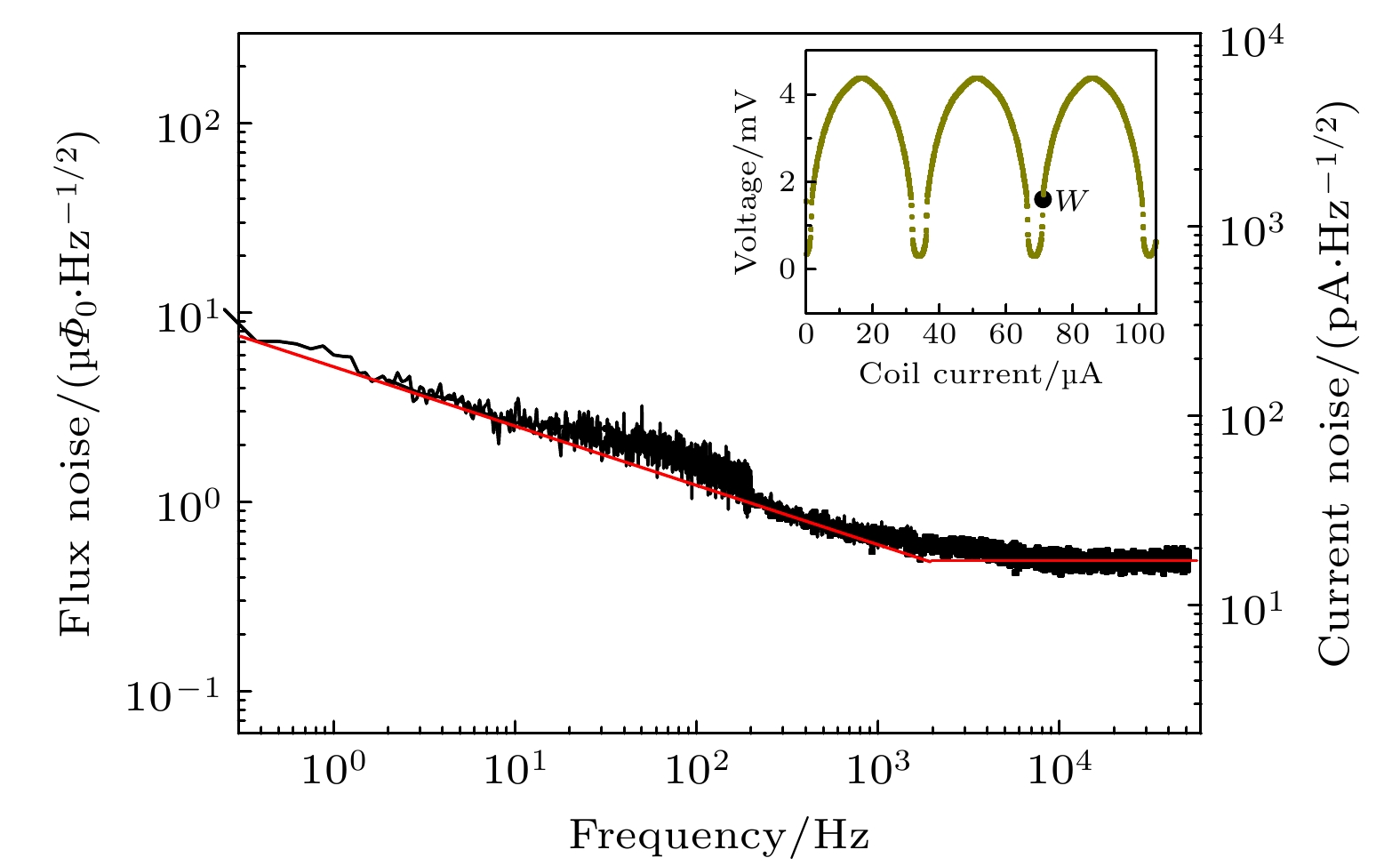
-
Superconducting quantum interference device (SQUID) has been used as an extremely sensitive flux sensor up to now. Series SQUID array (SSA) is made up of several identical element-SQUIDs in series, in which each element-SQUID is coupled with the same set of input coils by mutual inductance to realize the amplified output of the input current. From the noise viewpoint, each element-SQUID in SSA is independent of each other, resulting in the total voltage noise across the array rising linearly with the square root of the number of element-SQUIDs. From the perspective of input signals, since the signals come from the same set of input coils, the voltage output of the array is enlarged with the proportion of element-SQUID number, N. Taken together, the signal-to-noise ratio of SSA is increased by
$\sqrt{ {N}}$ times, or the flux noise of SSA is reduced by 1/$\sqrt{ {N}}$ times compared with that of an element-SQUID ideally. However, with the increase in the number of element-SQUIDs in series, the chip design of SSA becomes more complicated, which puts forward higher requirements for the consistency and stability of its fabrication process. Besides, there exists a certain flux coherence between element-SQUIDs in SSA, whose normal operation depends on the working state of each element-SQUID in the array. In this paper, the fabrication of series SQUID array is carried on the autonomous superconducting micro-nano process platform, with a yield rate reaching over 80% on a 4-inch standard silicon wafer. Two kinds of SSAs with 200 and 800 element-SQUIDs, respectively, are integrated in a meandering way on a chip in a millimeter area. Home-made directly-coupled readout circuit is used to obtain the characteristics of SSA. The experimental results reveal that the flux noise at best working point is as low as 0.5μ$\varPhi _{\text{0}}/\sqrt{\text{Hz}}$ and the current sensitivity is about 35 μA/Φ0, thus, the equivalent input current noise is achieved at a level of 18 pA/$ \sqrt{\text{Hz}} $ . Additionally, the dependence of relevant parameters in array on the number of element-SQUIDs is verified, which is consistent with theoretical expectation basically. These show that the reliability of device design and the consistency of fabrication process perform well, thus laying the technical foundation for developing the low-noise SQUID amplifier and the multiplexed readout of low-impedance detectors.-
Keywords:
- superconducting quantum interference device /
- flux noise /
- superconducting fabrication process
[1] Deaver B S, Fairbank W M 1961 Phys. Rev. Lett. 7 4
[2] Doll R, Näbauer M 1961 Phys. Rev. Lett. 7 51
Google Scholar
[3] Josephson B D 1962 Phys. Lett. 1 251
Google Scholar
[4] Josephson B D 1965 Adv. Phys. 14 419
Google Scholar
[5] Forgacs R L, Warnick A 1967 Rev. Sci. Instrum. 38 214
Google Scholar
[6] Drung D, Cantor R, Peters M, Scheer H J, Koch H 1990 Appl. Phys. Lett. 57 406
Google Scholar
[7] Wang Y, Zhang G, Zhang S, Rong L, Xie X 2020 Physica C 569 1353590
Google Scholar
[8] Seppä H, Ahonen A, Knuutila J, Simola J, Vikman V 1991 IEEE Trans. Magn. 27 2488
Google Scholar
[9] Drung D 2010 Supercond. Sci. Technol. 23 065006
Google Scholar
[10] Adelerhof D J, Kawai J, Uehara G, Kado H 1994 Appl. Phys. Lett. 65 2606
Google Scholar
[11] Kang C S, Kim K, Lee S J, Hwang S M, Kim J M, Yu K K, Kwon H, Lee S K, Lee Y H 2011 J. Appl. Phys. 110 053906
Google Scholar
[12] Xie X, Zhang Y, Wang H, Wang Y, Mück M, Dong H, Krause H J, Braginski A I, Offenhäusser A, Jiang M 2010 Supercond. Sci. Technol. 23 065016
Google Scholar
[13] Kazami K, Kawai J, Uehara G, Kado H 1996 Jpn. J. Appl. Phys. 35 4322
Google Scholar
[14] Falferi P, Mezzena R, Vinante A 2009 Supercond. Sci. Technol. 22 075020
Google Scholar
[15] Kiviranta M, Gronberg L, Sipola H 2011 Supercond. Sci. Technol. 24 045003
Google Scholar
[16] Welty R P, Martinis J M 1991 IEEE Trans. Magn. 27 2924
Google Scholar
[17] Welty R P, Martinis J M 1993 IEEE Trans. Magn. 3 2605
Google Scholar
[18] Morooka T, Myoren H, Takada S, Chinone K 2003 Jpn. J. Appl. Phys. 42 1375
Google Scholar
[19] Morooka T, Tanaka K, Chinone K 2002 IEEE Trans. Appl. Supercond. 12 1866
Google Scholar
[20] Lanting T, Dobbs M, Spieler H, Lee A T, Yamamoto Y 2009 Rev. Sci. Instrum. 80 094501
Google Scholar
[21] Li K, Hubbell S P 1995 IEEE Trans. Appl. Supercond. 5 3255
Google Scholar
[22] Stawiasz K G, Ketchen M B 1993 IEEE Trans. Appl. Supercond. 3 1808
Google Scholar
[23] Semenov V K, Khapaev M M 2016 IEEE Trans. Appl. Supercond. 26 1300710
Google Scholar
-
图 1 串联SQUID阵列(SSA)示意图. Ii和If分别表示通过输入线圈和反馈线圈的电流, Vo表示在偏置电流为Ib时SSA的输出电压
Figure 1. Schematic diagram of series SQUID array (SSA). Ii and If represent the current through the input coil and feedback coil, respectively. Vo is the output voltage of SSA biased at the current Ib.
图 2 (a) SSA光镜图; (b) SSA局部放大图
Figure 2. (a) Microscope photograph of global and (b) partial enlargement of SSA.
图 3 SSA平面工艺截面示意图
Figure 3. Cross section of SSA fabrication process.
图 4 (a) SSA电流-电压特性曲线; (b) SSA在不同偏置电流下的电压-线圈电流(磁通)特性曲线
Figure 4. (a) Current-voltage characteristic of SSA; (b) voltage-coil current (flux) characteristic at different bias currents of SSA.
图 5 SSA磁通噪声曲线和等效电流噪声
Figure 5. Flux noise curve and equivalent current noise of SSA
图 6 (a) SSA的正常态电阻Rn(方点)和最大电压调制幅度Vpp(星点)与SQUID数量之间的关系, 实线和虚线均为测试数据的线性拟合; (b) SSA的最大磁通-电压转换系数VΦ与SQUID数量之间的关系, 其中点为测试值, 线为线性拟合的结果
Figure 6. (a) Normal resistance Rn (square dot) and maximum voltage swing Vpp (star dot) of SSA dependence on the SQUID-element number, in which the solid and dashed line are linear fittings, respectively (b) maximum flux-to-voltage coefficient VΦ dependence on the SQUID-element number, where the dots are experimental data and the line is the result of linear fitting.
表 1 SSA设计参数
Table 1. Design parameters of SSA.
参数 符号 数值 约瑟夫森结面积/(μm × μm) A 3 × 3 临界电流/μA Ic 9 结并联电阻/Ω Rs 1和4 垫圈尺寸/(μm × μm) — 8 × 28 单个SQUID电感/pH LS 100 输入线圈匝数/匝 — 2 输入线圈线宽/μm — 1 SQUID个数 N 200和800 输入电流灵敏度/(μA·$ \varPhi_0^{–1} $) 1/Mi 35 
DownLoad: CSV
-
[1] Deaver B S, Fairbank W M 1961 Phys. Rev. Lett. 7 4
[2] Doll R, Näbauer M 1961 Phys. Rev. Lett. 7 51
Google Scholar
[3] Josephson B D 1962 Phys. Lett. 1 251
Google Scholar
[4] Josephson B D 1965 Adv. Phys. 14 419
Google Scholar
[5] Forgacs R L, Warnick A 1967 Rev. Sci. Instrum. 38 214
Google Scholar
[6] Drung D, Cantor R, Peters M, Scheer H J, Koch H 1990 Appl. Phys. Lett. 57 406
Google Scholar
[7] Wang Y, Zhang G, Zhang S, Rong L, Xie X 2020 Physica C 569 1353590
Google Scholar
[8] Seppä H, Ahonen A, Knuutila J, Simola J, Vikman V 1991 IEEE Trans. Magn. 27 2488
Google Scholar
[9] Drung D 2010 Supercond. Sci. Technol. 23 065006
Google Scholar
[10] Adelerhof D J, Kawai J, Uehara G, Kado H 1994 Appl. Phys. Lett. 65 2606
Google Scholar
[11] Kang C S, Kim K, Lee S J, Hwang S M, Kim J M, Yu K K, Kwon H, Lee S K, Lee Y H 2011 J. Appl. Phys. 110 053906
Google Scholar
[12] Xie X, Zhang Y, Wang H, Wang Y, Mück M, Dong H, Krause H J, Braginski A I, Offenhäusser A, Jiang M 2010 Supercond. Sci. Technol. 23 065016
Google Scholar
[13] Kazami K, Kawai J, Uehara G, Kado H 1996 Jpn. J. Appl. Phys. 35 4322
Google Scholar
[14] Falferi P, Mezzena R, Vinante A 2009 Supercond. Sci. Technol. 22 075020
Google Scholar
[15] Kiviranta M, Gronberg L, Sipola H 2011 Supercond. Sci. Technol. 24 045003
Google Scholar
[16] Welty R P, Martinis J M 1991 IEEE Trans. Magn. 27 2924
Google Scholar
[17] Welty R P, Martinis J M 1993 IEEE Trans. Magn. 3 2605
Google Scholar
[18] Morooka T, Myoren H, Takada S, Chinone K 2003 Jpn. J. Appl. Phys. 42 1375
Google Scholar
[19] Morooka T, Tanaka K, Chinone K 2002 IEEE Trans. Appl. Supercond. 12 1866
Google Scholar
[20] Lanting T, Dobbs M, Spieler H, Lee A T, Yamamoto Y 2009 Rev. Sci. Instrum. 80 094501
Google Scholar
[21] Li K, Hubbell S P 1995 IEEE Trans. Appl. Supercond. 5 3255
Google Scholar
[22] Stawiasz K G, Ketchen M B 1993 IEEE Trans. Appl. Supercond. 3 1808
Google Scholar
[23] Semenov V K, Khapaev M M 2016 IEEE Trans. Appl. Supercond. 26 1300710
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4464
- PDF Downloads: 101
- Cited By: 0
