-
Silicon is considered as a first candidate for ideal anode material of the next-generation lithium-ion battery due to its high theoretical capacity to meet the demand for higher energy density. On the other hand, high theoretical capacity is accompanied by massive volume expansion, which gives arise to high stress and crack and pulverization of anode particles. Finally, the capacity of the battery fades gradually. While some kinds of factors contribute to the failure of silicon-based electrodes, the most important one is the diffusion-induced stress generated in silicon-based electrode particles. The cyclic processes of lithiation and delithiation are accomplished by the intercalation into and deintercalation from the silicon particles of lithium ions. During the cycle, physical processes and chemical processes, such as diffusion of lithium ions, phase transition, and volume expansion, take place simultaneously, making the cyclic process a strong-coupling problem to be addressed. For example, the intercalation of lithium ions into the electrode results in volume expansion and phase transition of anodes, thereby inducing stress; in turn, stress affects the diffusion process of lithium ions. Aiming to probe this problem, with the finite deformation hypothesis, an electrochemical-mechanical coupling model is used to study the variation and distribution of concentration and stress of core-shell structure during lithiation. And more importantly, great emphasis is put on the optimal design of core-shell structure. The numerical results show that the shell is useful in prohibiting the volume expansion of silicon core, but large compressive radial stress in silicon core may cause the core and shell to be detached, while the tangential tensile stress at the core-shell interface leads the shell to fracture. To improve the electrochemical and mechanical performance and hence lengthen the cycle life of lithium-ion batteries, two kinds of optimal designs are considered: 1) single-layered core-shell structure and 2) double-layered core-shell structure. The numerical results suggest that the softer shell material is suitable for a single-layered core-shell structure and the inner-soft & outer-hard design is optimal for the double-layered core-shell structure. Furthermore, the effects of Young's modulus of the inner and outer carbon layer materials on the chemical and mechanical performance of anode are explored. The simulation shows that the optimal Young's modulus of the inner shell is less than 10 GPa, and that of the outer shell is not higher than 70 GPa. This research is helpful in designing and optimizing the silicon-based anode electrodes of lithium-ion batteries.
-
Keywords:
- lithium-ion battery /
- electrochemical-mechanical coupling /
- core-shell structure /
- finite deformation
[1] 程昀, 李劼, 贾明, 汤依伟, 杜双龙, 艾立华, 殷宝华, 艾亮 2015 64 210202
Google Scholar
Cheng Y, Li J, Jia M, Tang Y W, Du S L, Ai L H, Yin B H, Ai L 2015 Acta Phys. Sin. 64 210202
Google Scholar
[2] Li M, Lu J, Chen Z, Khalil A 2018 Adv. Mater. 30 1800561
Google Scholar
[3] Xie Z, Ma Z, Wang Y, Zhou Y, Lu C 2016 RSC Adv. 6 22383
Google Scholar
[4] Vetter J, Novák P, Wagner M R, Veit C, Möller K C, Besenhard J O, Winter M, Wohlfahrt-Mehrens M, Vogler C, Hammouche A 2005 J. Power Sources 147 269
Google Scholar
[5] 孙凤楠, 冯露, 卜家贺, 张静, 李林安, 王世斌 2019 68 120201
Google Scholar
Sun F N, Feng L, Bu J H, Zhang J, Li L A, Wang S B 2019 Acta Phys. Sin. 68 120201
Google Scholar
[6] Baggetto L, Niessen R A H, Roozeboom F, Notten P H L 2008 Adv. Funct. Mater. 18 1057
Google Scholar
[7] Panat R 2015 Thin Solid Films 596 174
Google Scholar
[8] Zhao Y, Stein P, Bai Y, Al-Siraj M, Yang Y, Xu B X 2019 J. Power Sources 413 259
Google Scholar
[9] Prussin S 1961 J. Appl. Phys. 32 1876
Google Scholar
[10] Zhang X, Shyy W, Sastry A M 2007 J. Electrochem. Soc. 154 A910
Google Scholar
[11] Song Y, Lu B, Ji X, Zhang J 2012 J. Electrochem. Soc. 159 A2060
Google Scholar
[12] Bagheri A, Arghavani J, Naghdabadi R 2019 Mech. Mater. 137 103134
Google Scholar
[13] Lu Y, Zhang P, Wang F, Zhang K, Zhao X 2018 Electrochim. Acta 274 359
Google Scholar
[14] Christensen J 2010 J. Electrochem. Soc. 157 A366
Google Scholar
[15] Zhang X Y, Hao F, Chen H S, Fang D N 2014 J. Electrochem. Soc. 161 A2243
Google Scholar
[16] Cheng Y T, Verbrugge M W 2008 J. Appl. Phys. 104 1876
[17] Deluca C M, Maute K, Dunn M L 2011 J. Power Sources 196 9672
Google Scholar
[18] Li Y, Zhang K, Zheng B, Zhang X Q, Wang Q 2015 J. Appl. Phys. 117 245103
[19] Hu B, Ma Z S, Lei W X, Zou Y L, Lu C S 2017 Theor. Appl. Mech. Lett. 7 199
Google Scholar
[20] Zhao Y F, Lu B, Zhang J 2018 Acta. Mech. Solida. Sin. 31 290
Google Scholar
[21] Gao X, Lu W, Xu J 2020 J. Power Sources 449 227501
Google Scholar
[22] Hao F, Fang D 2013 J. Electrochem. Soc. 160 A595
Google Scholar
[23] Zhao K J, Pharr M, Hartle L, Vlassak J J, Suo Z G 2012 J. Power Sources 218 6
Google Scholar
[24] Wu B, Lu W 2017 J. Phys. Chem. C 121 19022
Google Scholar
[25] Zhang Y, Zhu Z 2020 Int. J. Adv. Manuf. Technol. 108 499
Google Scholar
[26] Bohn E, Eckl T, Kamlah M, McMeekingc R 2013 J. Electrochem. Soc. 160 A1638
Google Scholar
[27] Zhang X, Chen H S, Fang D 2019 Int. J. Mech. Sci. 169 105323
[28] Xu C, Weng L, Chen B, Zhou J Q, Cai R 2019 Int. J. Mech. Sci. 157 87
[29] Zhao K, Pharr M, Cai S, Vlassak J J, Suo Z G 2011 J. Am. Ceram. Soc. 94 s226
Google Scholar
[30] Zhang K, Zheng B, Yang F, Li Y 2020 Int. J. Mech. Sci. 177 105602
Google Scholar
[31] Liu B H, Wang X, Chen H S, Chen S, Yang H X, Xu J, Jiang H Q, Fang D N 2019 J. Appl. Mech. 86 041005
Google Scholar
[32] Ding N, Xu J, Yao Y X, Wegner G, Fang X, . Chen C.H, Lieberwirth I 2009 Solid State Ionics 180 222
Google Scholar
[33] Sethuraman V A, Chon M J, Shimshak M, Winkle N V, Guduru P R 2010 Electrochem. Commun. 12 1614
Google Scholar
[34] Wu B, Lu W 2017 J. Power Sources 360 360
Google Scholar
[35] Deng Q, Hu R, Xu C, Chen B, Zhou J 2019 J. Solid State Electrochem. 23 2999
Google Scholar
-
图 1 锂离子电池的用途
Figure 1. Usage of lithium-ion batteries.
图 2 电化学-力学耦合机理
Figure 2. Electrochemistry-mechanics coupling mechanism.
图 3 (a) 锂离子电池核壳结构示意图; (b) 径向和切向示意图
Figure 3. (a) Schematic diagram of core-shell structure of lithium-ion battery; (b) radial and tangential schematic diagram.
图 4 不同假设条件下充电过程中沿着半径方向的径向应力和切向应力 (a)小变形下的径向应力; (b)有限变形下的径向应力; (c)小变形下的切向应力; (d)有限变形下的切向应力
Figure 4. Radial stress and tangential stress along the radial direction during charging under different hypothesis: (a) Radial stress under small deformation; (b) radial stress under finite deformation; (c) tangential stress under small deformation; (d) tangential stress under finite deformation.
图 5 嵌锂过程中沿着半径方向的(a)浓度和(b) von Mises 应力分布示意图
Figure 5. Schematic diagram of (a) concentration; (b) von Mises stress along the radius during lithium insertion.
图 6 嵌锂过程中(a)浓度, (b) von Mises应力, (c)径向应力, (d)切向应力随着时间的分布示意
Figure 6. Schematic diagram of the distribution of (a) concentration, (b) von Mises stress, (c) radial stress, and (d) tangential stress over time during lithium insertion.
图 7 双层核壳结构在嵌锂过程(a)浓度, (b) von Mises应力, (c)径向应力, (d)切向应力的分布示意图
Figure 7. Schematic diagram of the distribution of the double-layer core-shell structure during lithium insertion process: (a) concentration; (b) von Mises stress; (c) radial stress; and (d) tangential stress.
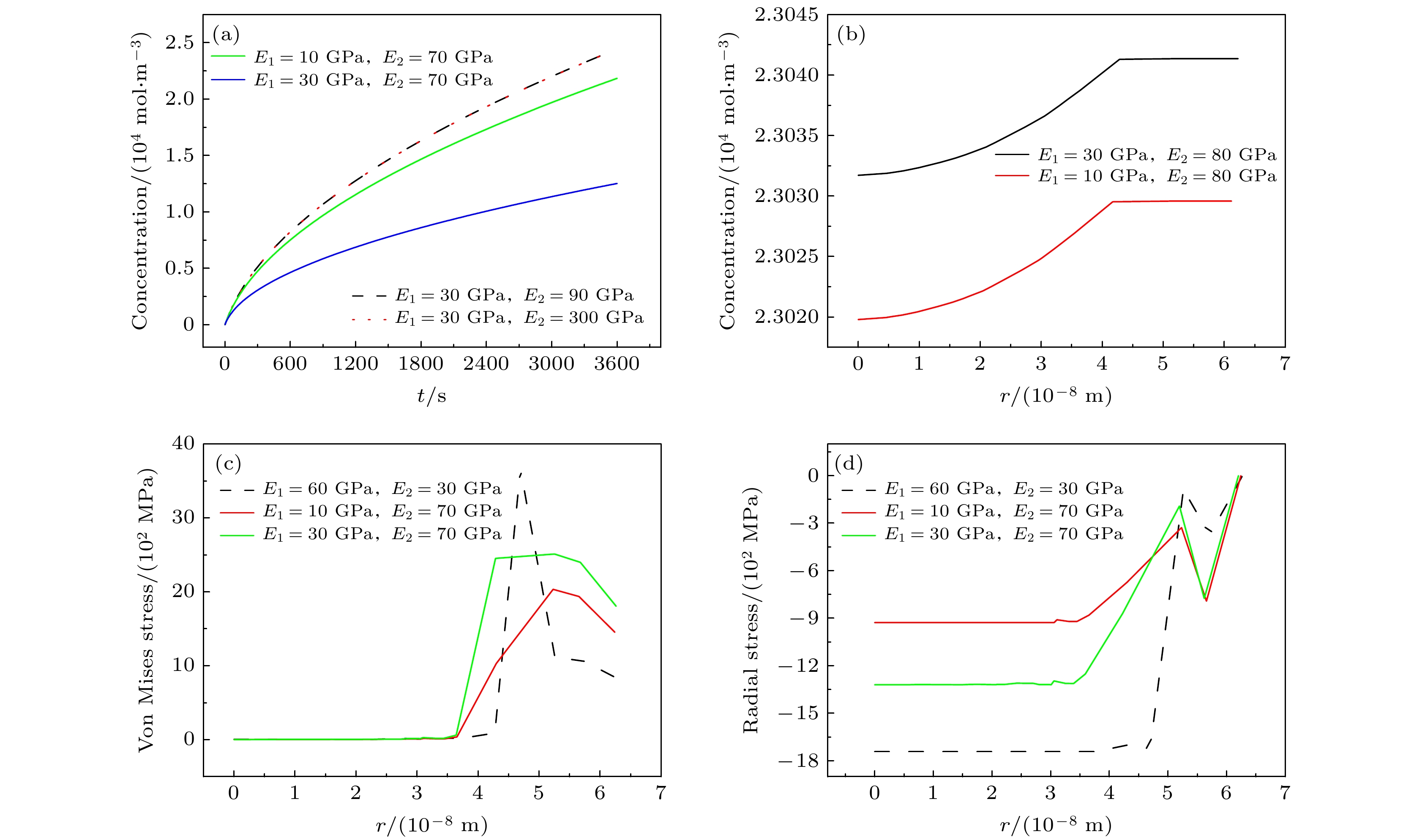
图 8 Si/C1/C3双层核壳结构和Si/C3/C1双层核壳结构的(a)浓度, (b) von Mises应力, (c)径向应力, (d)切向应力分布示意图
Figure 8. (a) Concentration, (b) von Mises stress, (c) radial stress, and (d) tangential stress distribution schematic diagram of Si/C1/C3 double-layer core-shell structure and Si/C3/C1 double-layer core-shell structure.
图 9 不同的内外层壳杨氏模量情况下 (a)浓度, (b)浓度, (c) von Mises应力, (d)径向应力分布示意图
Figure 9. (a) Concentration, (b) concentration, (c) von Mises stress, (d) schematic diagram of radial stress distribution under different Young's modulus of inner and outer shells.
参数 核 壳 饱和浓度 Cmax/(mol·m–3) 2.95 × 105 2.4 × 104 初始浓度C0/(mol·m–3) 0 0 扩散系数 D/(m2·s–1) 1.0 × 10–16 1.45 × 10–13 内径/外径 R/m 4 × 10–8 5 × 10–8 泊松比 ν 0.23 0.30 杨氏模量E/Pa 8 × 1010 6 × 1010 偏摩尔体积 Ω/(m3·mol–1) 3/Cmax 3.497 × 10–6 室温 T/K 298 
DownLoad: CSV
-
[1] 程昀, 李劼, 贾明, 汤依伟, 杜双龙, 艾立华, 殷宝华, 艾亮 2015 64 210202
Google Scholar
Cheng Y, Li J, Jia M, Tang Y W, Du S L, Ai L H, Yin B H, Ai L 2015 Acta Phys. Sin. 64 210202
Google Scholar
[2] Li M, Lu J, Chen Z, Khalil A 2018 Adv. Mater. 30 1800561
Google Scholar
[3] Xie Z, Ma Z, Wang Y, Zhou Y, Lu C 2016 RSC Adv. 6 22383
Google Scholar
[4] Vetter J, Novák P, Wagner M R, Veit C, Möller K C, Besenhard J O, Winter M, Wohlfahrt-Mehrens M, Vogler C, Hammouche A 2005 J. Power Sources 147 269
Google Scholar
[5] 孙凤楠, 冯露, 卜家贺, 张静, 李林安, 王世斌 2019 68 120201
Google Scholar
Sun F N, Feng L, Bu J H, Zhang J, Li L A, Wang S B 2019 Acta Phys. Sin. 68 120201
Google Scholar
[6] Baggetto L, Niessen R A H, Roozeboom F, Notten P H L 2008 Adv. Funct. Mater. 18 1057
Google Scholar
[7] Panat R 2015 Thin Solid Films 596 174
Google Scholar
[8] Zhao Y, Stein P, Bai Y, Al-Siraj M, Yang Y, Xu B X 2019 J. Power Sources 413 259
Google Scholar
[9] Prussin S 1961 J. Appl. Phys. 32 1876
Google Scholar
[10] Zhang X, Shyy W, Sastry A M 2007 J. Electrochem. Soc. 154 A910
Google Scholar
[11] Song Y, Lu B, Ji X, Zhang J 2012 J. Electrochem. Soc. 159 A2060
Google Scholar
[12] Bagheri A, Arghavani J, Naghdabadi R 2019 Mech. Mater. 137 103134
Google Scholar
[13] Lu Y, Zhang P, Wang F, Zhang K, Zhao X 2018 Electrochim. Acta 274 359
Google Scholar
[14] Christensen J 2010 J. Electrochem. Soc. 157 A366
Google Scholar
[15] Zhang X Y, Hao F, Chen H S, Fang D N 2014 J. Electrochem. Soc. 161 A2243
Google Scholar
[16] Cheng Y T, Verbrugge M W 2008 J. Appl. Phys. 104 1876
[17] Deluca C M, Maute K, Dunn M L 2011 J. Power Sources 196 9672
Google Scholar
[18] Li Y, Zhang K, Zheng B, Zhang X Q, Wang Q 2015 J. Appl. Phys. 117 245103
[19] Hu B, Ma Z S, Lei W X, Zou Y L, Lu C S 2017 Theor. Appl. Mech. Lett. 7 199
Google Scholar
[20] Zhao Y F, Lu B, Zhang J 2018 Acta. Mech. Solida. Sin. 31 290
Google Scholar
[21] Gao X, Lu W, Xu J 2020 J. Power Sources 449 227501
Google Scholar
[22] Hao F, Fang D 2013 J. Electrochem. Soc. 160 A595
Google Scholar
[23] Zhao K J, Pharr M, Hartle L, Vlassak J J, Suo Z G 2012 J. Power Sources 218 6
Google Scholar
[24] Wu B, Lu W 2017 J. Phys. Chem. C 121 19022
Google Scholar
[25] Zhang Y, Zhu Z 2020 Int. J. Adv. Manuf. Technol. 108 499
Google Scholar
[26] Bohn E, Eckl T, Kamlah M, McMeekingc R 2013 J. Electrochem. Soc. 160 A1638
Google Scholar
[27] Zhang X, Chen H S, Fang D 2019 Int. J. Mech. Sci. 169 105323
[28] Xu C, Weng L, Chen B, Zhou J Q, Cai R 2019 Int. J. Mech. Sci. 157 87
[29] Zhao K, Pharr M, Cai S, Vlassak J J, Suo Z G 2011 J. Am. Ceram. Soc. 94 s226
Google Scholar
[30] Zhang K, Zheng B, Yang F, Li Y 2020 Int. J. Mech. Sci. 177 105602
Google Scholar
[31] Liu B H, Wang X, Chen H S, Chen S, Yang H X, Xu J, Jiang H Q, Fang D N 2019 J. Appl. Mech. 86 041005
Google Scholar
[32] Ding N, Xu J, Yao Y X, Wegner G, Fang X, . Chen C.H, Lieberwirth I 2009 Solid State Ionics 180 222
Google Scholar
[33] Sethuraman V A, Chon M J, Shimshak M, Winkle N V, Guduru P R 2010 Electrochem. Commun. 12 1614
Google Scholar
[34] Wu B, Lu W 2017 J. Power Sources 360 360
Google Scholar
[35] Deng Q, Hu R, Xu C, Chen B, Zhou J 2019 J. Solid State Electrochem. 23 2999
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 8160
- PDF Downloads: 364
- Cited By: 0
