Molecular dynamics simulation of helium bubble ultimate pressure in α-Fe

Li Xiang; Yin Yi-Hui; Zhang Yuan-Zhang

doi:10.7498/aps.70.20201409

Abstract

In order to understand further the micro-mechanism of helium bubble punching out of the dislocation loop in α-Fe, it is necessary to study the ultimate pressure characteristics of helium bubble punching out of the dislocation loop. In this paper, a cubic representative volume element (RVE) model of the metal-helium bubble is established. For eight types of spherical helium bubbles with different initial radii, molecular dynamics simulations are carried out with the initial helium-to-vacancy ratio serving as a variable and the ultimate pressure of helium bubble and the critical helium-to-vacancy ratio at the beginning of dislocation loop formation in each model are obtained. The results show that for helium bubbles with dimensionless radius ranging from 2 to 10, both the ultimate pressure and the critical helium-to-vacancy ratio of helium bubble punching out of the dislocation loop decrease nonlinearly with the increase of initial helium bubble radius. The relationships of the ultimate pressure and the critical helium-to-vacancy ratio with the initial radius of helium bubble are fitted respectively according to the simulation results and the fitted two equations are in good agreement with the results of previous theoretical studies. The critical helium-to-vacancy ratio required for helium bubble punching out of the dislocation loop in α-Fe has an obvious size effect. For the helium bubble in the late nucleation stage (e.g. helium bubble with an initial radius of 0.81 nm) and non-ideal gas stage (e.g. helium bubble with an initial radius ranging from 1.00 nm to 2.50 nm), the critical helium-to-vacancy ratios for punching out of the dislocation loop are the same as the initial helium-to-vacancy ratio corresponding to the peak pressure point of helium bubble. But for early or middle nucleation stage, such as helium bubble with an initial radius of 0.50 nm, the critical helium-to-vacancy ratio for punching out of the dislocation loop is about 13.46% greater than the initial helium-to-vacancy ratios corresponding to the peak pressure points. At the initial moment (0 ps), in the cross section passing through the center of cubic RVE, the shear stress is concentrated, and the maximum shear stress of Fe atom array around the helium bubble is located at the intersection points (i.e. at 45°) of diagonal and helium bubble boundary, and it is distributed symmetrically with respect to the double fold lines of the cross section parallel to the sides. Both the range of shear stress concentrating area and the maximum shear stress increase with the initial helium-to-vacancy ratio increasing. The dislocation loop’s punching direction corresponds to the direction of the maximum shear stress. The research in this paper can deepen the understanding of the physical properties of helium bubbles in metals and lay a useful foundation for the subsequent analyzing of the effects of helium bubbles on the macroscopic physical and mechanical properties of materials.

Keywords:

Authors and contacts

1.
Institute of Systems Engineering, China Academy of Engineering Physics, Mianyang 621999, China
2.
School of Applied Technology, Southwest University of Science and Technology, Mianyang 621010, China

Corresponding author: Yin Yi-Hui, yinyh@caep.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 11572298) and the Young Scientists Fund of the National Natural Science Foundation of China (Grant No. 11702280)

FullText HTML : translate this paragraph

References

[1]	王佩璇, 宋家树 2002 材料中的氦及氚渗透 (第1版) (北京: 国防工业出版社) 第1−52页 Wang P X, Song J S 2002 Helium and Permeation of Tritium in Materials (1st Ed.) (Bejing: National Defense Industry Press) pp1−52
[2]	Trinkaus H, Singh B N 2003 J. Nucl. Mater. 323 229 Google Scholar
[3]	Barnes R S 1965 Nature 206 1307 Google Scholar
[4]	Wang Z J, Allen F I, Shan Z W, Hosemann P 2016 Acta Mater. 121 78 Google Scholar
[5]	彭述明, 王和义 2015 氚化学与工艺学 (第1版) (北京: 国防工业出版社) 第1−51页 Peng S M, Wang H Y 2015 Tritium Chemistry and Technology (1st Ed.) (Bejing: National Defense Industry Press) pp1−51
[6]	刘远东, 尹益辉, 谭云, 孙颖, 梅军 2011 中国科学技术科学 54 1 Google Scholar Liu Y D, Yin Y H, Tan Y, Sun Y, Mei J 2011 Sci. China Tech. Sci. 54 1 Google Scholar
[7]	刘远东, 尹益辉, 谭云 2012 61 156601 Google Scholar Liu Y D, Yin Y H, Tan Y 2012 Acta Phys. Sin. 61 156601 Google Scholar
[8]	尹益辉, 刘远东, 陈长安, 谭云 2016 中国科学技术科学 46 1071 Google Scholar Yin Y H, Liu Y D, Chen C A, Tan Y 2016 Sci. Sin. Tech. 46 1071 Google Scholar
[9]	Liu P P, Zhan Q, Fu Z Y, Wei Y P, Wang Y M, Wang F M, Ohnuki S, Wan F R 2015 J. Alloys Compd. 649 859 Google Scholar
[10]	Krsjak V, Degmova J, Sojak S, Slugen V 2018 J. Nucl. Mater. 499 38 Google Scholar
[11]	Taverna D, Kociak M, Stéphan O, Fabre A, Finot E, Décamps B, Colliex C 2008 Phys. Rev. Lett. 100 035301 Google Scholar
[12]	Fréchard S, Walls M, Kociak M, Chevalier J P, Henry J, Gorse D 2009 J. Nucl. Mater. 393 102 Google Scholar
[13]	Trinkaus H 1983 Radiat. Eff. 78 189 Google Scholar
[14]	郭立平, 罗凤凤, 于雁霞 2017 核材料辐照位错环 (第1版) (北京: 国防工业出版社) 第174−200页 Guo L P, Luo F F, Yu Y X 2017 Dislocation Loops in Irradiated Nuclear Materials (1st Ed.) (Bejing: National Defense Industry Press) pp174−200
[15]	Wolfer W G 1988 Philos. Mag. A 58 285 Google Scholar
[16]	Zhang Y, Yin Y, Zhao F, Deng K, Feng J, Li J, Yan G 2019 Steel Res. Int. 90 1 Google Scholar
[17]	Deng H Q, Hu W Y, Gao F, Heinisch H L, Hu S Y, Li Y L, Kurtz R J 2013 J. Nucl. Mater. 442 667 Google Scholar
[18]	Gao C, Tian D, Li M, Qian D 2018 Nucl. Instruments Methods Phys. Res. Sect. B Beam Interact. with Mater. Atoms 418 46 Google Scholar
[19]	Zhang B L, Wang J, Hou Q 2011 Chin. Phys. B 20 036105 Google Scholar
[20]	Hetherly J, Martinez E, Nastasi M, Caro A 2011 J. Nucl. Mater. 419 201 Google Scholar
[21]	Caro A, Hetherly J, Stukowski A, Caro M, Martinez E, Srivilliputhur S, Zepeda-Ruiz L, Nastasi M 2011 J. Nucl. Mater. 418 261 Google Scholar
[22]	Xie H, Gao N, Xu K, Lu G H, Yu T, Yin F 2017 Acta Mater. 141 10 Google Scholar
[23]	Caskey G R 1985 Fusion Technol. 8 2293 Google Scholar
[24]	Edmondson P D, Parish C M, Zhang Y, Hallén A, Miller M K 2013 J. Nucl. Mater. 434 210 Google Scholar
[25]	Zhang F, Wang X, Wierschke J B, Wang L 2015 Scr. Mater. 109 28 Google Scholar
[26]	Plimpton S 1995 J. Comput. Phys. 117 1 Google Scholar
[27]	梁力, 谈效华, 向伟, 王远, 程焰林, 马明旺 2015 64 046103 Google Scholar Liang L, Tan X H, Xiang W, Wang Y, Cheng Y L, Ma M W 2015 Acta Phys. Sin. 64 046103 Google Scholar
[28]	Ackland G J, Mendelev M I, Srolovitz D J, Han S, Barashev A V 2004 J. Phys. Condens. Matter 16 S2629 Google Scholar
[29]	Aziz R A, Janzen A R, Moldover M R 1995 Phys.Rev.Lett 74 1586 Google Scholar
[30]	Gao F, Deng H, Heinisch H L, Kurtz R J 2011 J. Nucl. Mater. 418 115 Google Scholar
[31]	Guo S H, Zhu B E, Liu W C, Pan Z Y, Wang Y X 2009 Nucl. Instruments Methods Phys. Res. Sect. B Beam Interact. with Mater. Atoms 267 3278 Google Scholar
[32]	Thompson A P, Plimpton S J, Mattson W 2009 J. Chem. Phys. 131 154107 Google Scholar
[33]	Rycroft, Chris H 2009 Chaos 19 41111 Google Scholar
[34]	Mills R L, Liebenberg D H, Bronson J C 1980 Phys. Rev. B 21 5137 Google Scholar
[35]	Stukowski A 2010 Model. Simul. Mater. Sci. Eng. 18 15012 Google Scholar
[36]	Stukowski A, Bulatov V V, Arsenlis A 2012 Model. Simul. Mater. Sci. Eng. 20 85007 Google Scholar
[37]	Evans J H 1978 J. Nucl. Mater. 76–77 228 Google Scholar
[38]	Martienssen W, Warlimont H 2005 Handbook of Condensed Matter and Materials Data (New York: Springer Berlin Heidelberg) pp132−134
[39]	Wolfer W G 1989 Philos. Mag. A 59 87 Google Scholar
[40]	Iwakiri H 2000 J. Nucl. Mater. 283-287 1134 Google Scholar
[41]	Donnelly S E 1985 Radiat. Eff. 90 1 Google Scholar
[42]	Trinkaus H 1989 Scr. Metall. 23 1773 Google Scholar

Cited By

图 1 含氦泡的α-Fe计算模型(图中He → He泡, Fe → Fe基体)

Figure 1. Model of α-Fe with helium bubble (In Fig. He → helium bubble, Fe → Fe matrix).

DownLoad: Full-Size Img PowerPoint

图 2 MD模拟结果与Mills等^[34]的实验结果对比(300 K)

Figure 2. Comparison of MD simulation results with experimental results of Mills et al.^[34] (300 K).

DownLoad: Full-Size Img PowerPoint

图 3 氦泡压强随初始氦空位比的变化

Figure 3. Changes of pressure of helium bubble with initial helium-to-vacancy ratio.

DownLoad: Full-Size Img PowerPoint

图 4 氦泡极限压强、临界氦空位比随氦泡初始半径的变化

Figure 4. Changes of ultimate pressure and critical helium-to-vacancy ratio of helium bubble with initial radius of helium bubble.

DownLoad: Full-Size Img PowerPoint

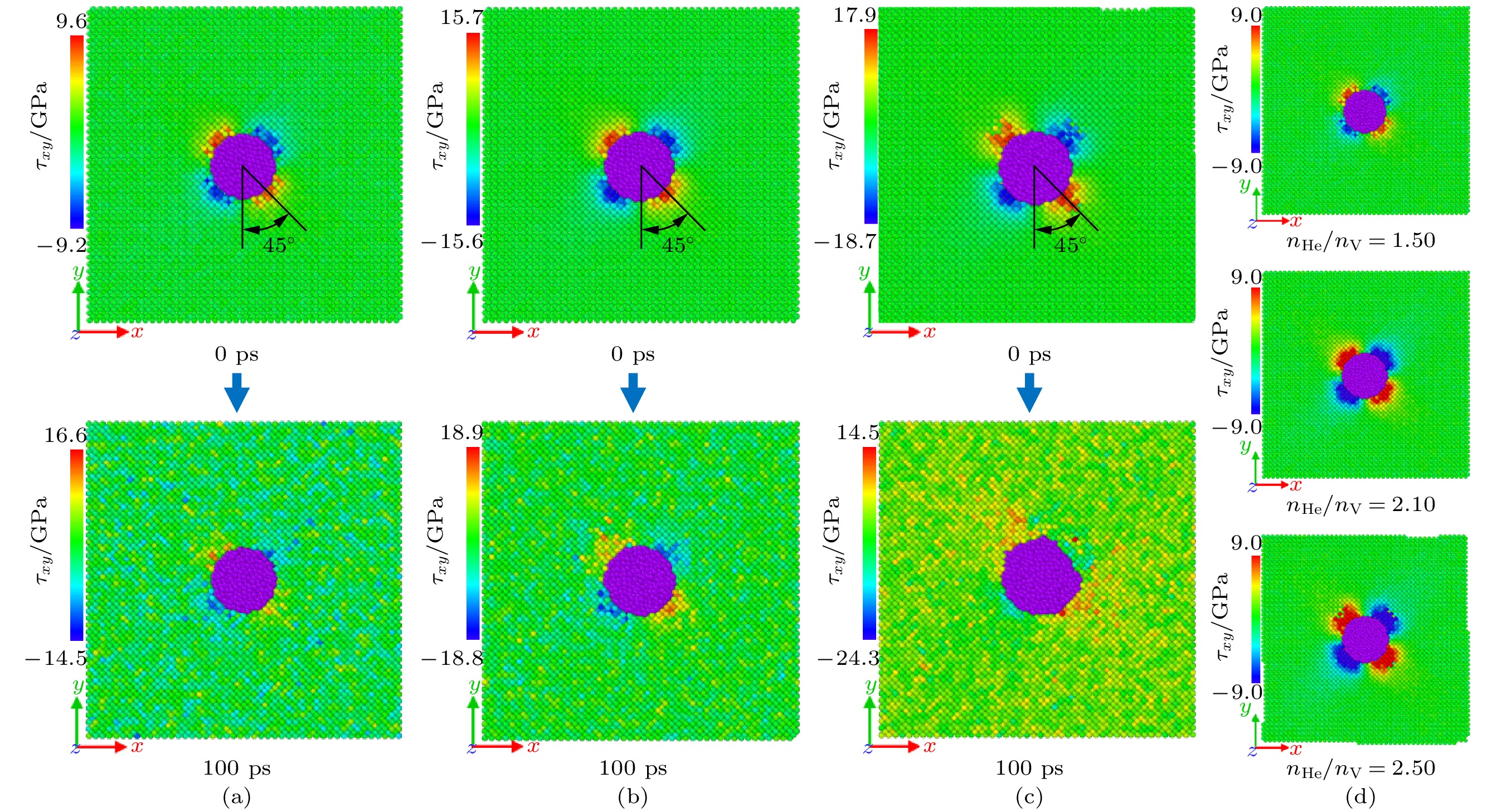
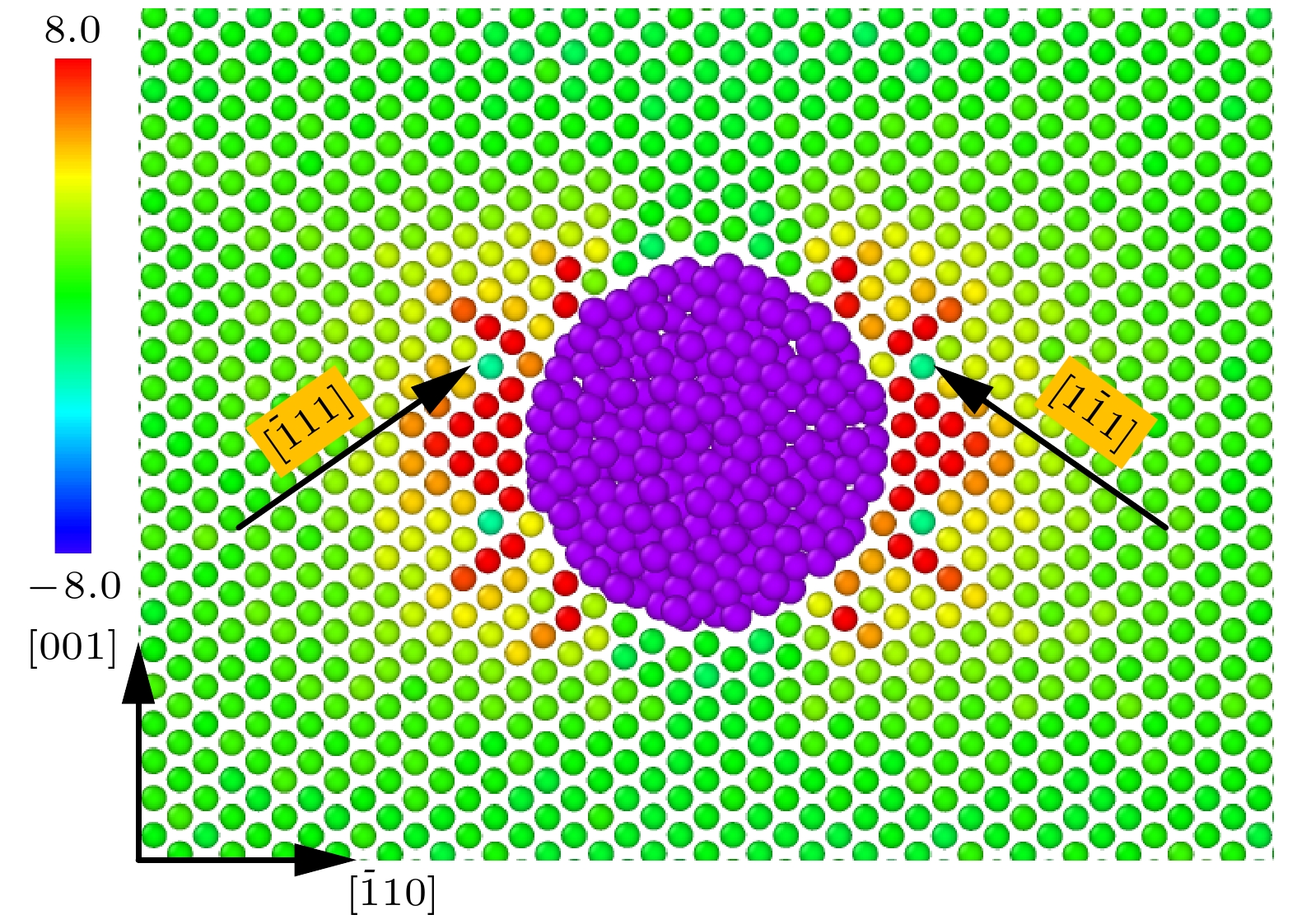
图 5 氦泡周围Fe原子阵列的剪应力分布　(a) n_He/n_V = 1.50; (b) n_He/n_V = 2.10; (c) n_He/n_V = 2.50; (d) 上下限相同时0 ps处的原子应力分布

Figure 5. Shear stress distribution of Fe atom array around helium bubble: (a) n_He/n_V = 1.50; (b) n_He/n_V = 2.10; (c) n_He/n_V = 2.50; (d) atomic stress distribution at 0 ps with the same upper and lower limit.

DownLoad: Full-Size Img PowerPoint

图 6 初始半径为1.31 nm, n_He/n_V = 2.10时氦泡冲出的位错环在xy平面投影　(a) 88 ps; (b) 92 ps; (c) 100 ps; (d)删除图6(c)中Fe原子后带缺陷网格的位错图

Figure 6. Projection of dislocation loops produced by helium bubbles in xy plane, when initial radius of helium bubble is 1.31 nm, n_He/n_V = 2.10: (a) 88 ps; (b) 92 ps; (c) 100 ps; (d) a dislocation picture with a defect mesh after removing the Fe atoms in Fig. 6(c).

DownLoad: Full-Size Img PowerPoint

图 7 (110)面原子剪应力分布(氦泡初始半径为1.31 nm, n_He/n_V = 2.10)

Figure 7. (110) Surface atomic shear stress distribution (initial radius of helium bubble is 1.31 nm, n_He/n_V = 2.10).

DownLoad: Full-Size Img PowerPoint

图 8 氦泡极限压强与氦泡初始半径关系

Figure 8. Ultimate pressure vs. initial radius of helium bubble.

DownLoad: Full-Size Img PowerPoint

map

[1]	王佩璇, 宋家树 2002 材料中的氦及氚渗透 (第1版) (北京: 国防工业出版社) 第1−52页 Wang P X, Song J S 2002 Helium and Permeation of Tritium in Materials (1st Ed.) (Bejing: National Defense Industry Press) pp1−52
[2]	Trinkaus H, Singh B N 2003 J. Nucl. Mater. 323 229 Google Scholar
[3]	Barnes R S 1965 Nature 206 1307 Google Scholar
[4]	Wang Z J, Allen F I, Shan Z W, Hosemann P 2016 Acta Mater. 121 78 Google Scholar
[5]	彭述明, 王和义 2015 氚化学与工艺学 (第1版) (北京: 国防工业出版社) 第1−51页 Peng S M, Wang H Y 2015 Tritium Chemistry and Technology (1st Ed.) (Bejing: National Defense Industry Press) pp1−51
[6]	刘远东, 尹益辉, 谭云, 孙颖, 梅军 2011 中国科学技术科学 54 1 Google Scholar Liu Y D, Yin Y H, Tan Y, Sun Y, Mei J 2011 Sci. China Tech. Sci. 54 1 Google Scholar
[7]	刘远东, 尹益辉, 谭云 2012 61 156601 Google Scholar Liu Y D, Yin Y H, Tan Y 2012 Acta Phys. Sin. 61 156601 Google Scholar
[8]	尹益辉, 刘远东, 陈长安, 谭云 2016 中国科学技术科学 46 1071 Google Scholar Yin Y H, Liu Y D, Chen C A, Tan Y 2016 Sci. Sin. Tech. 46 1071 Google Scholar
[9]	Liu P P, Zhan Q, Fu Z Y, Wei Y P, Wang Y M, Wang F M, Ohnuki S, Wan F R 2015 J. Alloys Compd. 649 859 Google Scholar
[10]	Krsjak V, Degmova J, Sojak S, Slugen V 2018 J. Nucl. Mater. 499 38 Google Scholar
[11]	Taverna D, Kociak M, Stéphan O, Fabre A, Finot E, Décamps B, Colliex C 2008 Phys. Rev. Lett. 100 035301 Google Scholar
[12]	Fréchard S, Walls M, Kociak M, Chevalier J P, Henry J, Gorse D 2009 J. Nucl. Mater. 393 102 Google Scholar
[13]	Trinkaus H 1983 Radiat. Eff. 78 189 Google Scholar
[14]	郭立平, 罗凤凤, 于雁霞 2017 核材料辐照位错环 (第1版) (北京: 国防工业出版社) 第174−200页 Guo L P, Luo F F, Yu Y X 2017 Dislocation Loops in Irradiated Nuclear Materials (1st Ed.) (Bejing: National Defense Industry Press) pp174−200
[15]	Wolfer W G 1988 Philos. Mag. A 58 285 Google Scholar
[16]	Zhang Y, Yin Y, Zhao F, Deng K, Feng J, Li J, Yan G 2019 Steel Res. Int. 90 1 Google Scholar
[17]	Deng H Q, Hu W Y, Gao F, Heinisch H L, Hu S Y, Li Y L, Kurtz R J 2013 J. Nucl. Mater. 442 667 Google Scholar
[18]	Gao C, Tian D, Li M, Qian D 2018 Nucl. Instruments Methods Phys. Res. Sect. B Beam Interact. with Mater. Atoms 418 46 Google Scholar
[19]	Zhang B L, Wang J, Hou Q 2011 Chin. Phys. B 20 036105 Google Scholar
[20]	Hetherly J, Martinez E, Nastasi M, Caro A 2011 J. Nucl. Mater. 419 201 Google Scholar
[21]	Caro A, Hetherly J, Stukowski A, Caro M, Martinez E, Srivilliputhur S, Zepeda-Ruiz L, Nastasi M 2011 J. Nucl. Mater. 418 261 Google Scholar
[22]	Xie H, Gao N, Xu K, Lu G H, Yu T, Yin F 2017 Acta Mater. 141 10 Google Scholar
[23]	Caskey G R 1985 Fusion Technol. 8 2293 Google Scholar
[24]	Edmondson P D, Parish C M, Zhang Y, Hallén A, Miller M K 2013 J. Nucl. Mater. 434 210 Google Scholar
[25]	Zhang F, Wang X, Wierschke J B, Wang L 2015 Scr. Mater. 109 28 Google Scholar
[26]	Plimpton S 1995 J. Comput. Phys. 117 1 Google Scholar
[27]	梁力, 谈效华, 向伟, 王远, 程焰林, 马明旺 2015 64 046103 Google Scholar Liang L, Tan X H, Xiang W, Wang Y, Cheng Y L, Ma M W 2015 Acta Phys. Sin. 64 046103 Google Scholar
[28]	Ackland G J, Mendelev M I, Srolovitz D J, Han S, Barashev A V 2004 J. Phys. Condens. Matter 16 S2629 Google Scholar
[29]	Aziz R A, Janzen A R, Moldover M R 1995 Phys.Rev.Lett 74 1586 Google Scholar
[30]	Gao F, Deng H, Heinisch H L, Kurtz R J 2011 J. Nucl. Mater. 418 115 Google Scholar
[31]	Guo S H, Zhu B E, Liu W C, Pan Z Y, Wang Y X 2009 Nucl. Instruments Methods Phys. Res. Sect. B Beam Interact. with Mater. Atoms 267 3278 Google Scholar
[32]	Thompson A P, Plimpton S J, Mattson W 2009 J. Chem. Phys. 131 154107 Google Scholar
[33]	Rycroft, Chris H 2009 Chaos 19 41111 Google Scholar
[34]	Mills R L, Liebenberg D H, Bronson J C 1980 Phys. Rev. B 21 5137 Google Scholar
[35]	Stukowski A 2010 Model. Simul. Mater. Sci. Eng. 18 15012 Google Scholar
[36]	Stukowski A, Bulatov V V, Arsenlis A 2012 Model. Simul. Mater. Sci. Eng. 20 85007 Google Scholar
[37]	Evans J H 1978 J. Nucl. Mater. 76–77 228 Google Scholar
[38]	Martienssen W, Warlimont H 2005 Handbook of Condensed Matter and Materials Data (New York: Springer Berlin Heidelberg) pp132−134
[39]	Wolfer W G 1989 Philos. Mag. A 59 87 Google Scholar
[40]	Iwakiri H 2000 J. Nucl. Mater. 283-287 1134 Google Scholar
[41]	Donnelly S E 1985 Radiat. Eff. 90 1 Google Scholar
[42]	Trinkaus H 1989 Scr. Metall. 23 1773 Google Scholar

[1]	Du Xiao-Jiao, Wei Long, Sun Yu, Hu Shui-Ming. Free electron laser prepared high-intensity metastable helium and helium-like ions. Acta Physica Sinica, 2024, 73(15): 150201. doi: 10.7498/aps.73.20240554
[2]	Zhou Liang-Fu, Zhang Jing, He Wen-Hao, Wang Dong, Su Xue, Yang Dong-Yang, Li Yu-Hong. The nucleation and growth of Helium hubbles at grain boundaries of bcc tungsten: a molecular dynamics simulation. Acta Physica Sinica, 2020, 69(4): 046103. doi: 10.7498/aps.69.20191069
[3]	Ma Yu-Tian, Liu Jun-Biao, Han Li, Tian Li-Feng, Wang Xue-Cong, Meng Xiang-Min, Xiao Shan-Qu, Wang Bo. Helium behavior of tungsten investigated by helium ion microscope. Acta Physica Sinica, 2019, 68(4): 040702. doi: 10.7498/aps.68.20181864
[4]	Liu Si-Mian, Han Wei-Zhong. Mechanism of interaction between interface and radiation defects in metal. Acta Physica Sinica, 2019, 68(13): 137901. doi: 10.7498/aps.68.20190128
[5]	Guo Hong-Yan, Xia Min, Yan Qing-Zhi, Guo Li-Ping, Chen Ji-Hong, Ge Chang-Chun. Microstructure of medium energy and high density helium ion implanted tungsten. Acta Physica Sinica, 2016, 65(7): 077803. doi: 10.7498/aps.65.077803
[6]	Liang Li, Tan Xiao-Hua, Xiang Wei, Wang Yuan, Cheng Yan-Lin, Ma Ming-Wang. A molecular dynamics study of temperature and depth effect on helium bubble released from Ti surface. Acta Physica Sinica, 2015, 64(4): 046103. doi: 10.7498/aps.64.046103
[7]	Xie Hui-Qiao, Tan Yi, Liu Yang-Qing, Wang Wen-Hao, Gao Zhe. A collisional-radiative model for the helium plasma in the sino-united spherical tokamak and its application to the line intensity ratio diagnostic. Acta Physica Sinica, 2014, 63(12): 125203. doi: 10.7498/aps.63.125203
[8]	Zheng Hui, Zhang Chong-Hong, Chen Bo, Yang Yi-Tao, Lai Xin-Chun. Inhibition effect of low-temperature pre-irradiation of helium ions on the growth of helium bubble in stainless steel：a Monte Carlo simulation. Acta Physica Sinica, 2014, 63(10): 106102. doi: 10.7498/aps.63.106102
[9]	Du Yang-Yang, Li Bing-Sheng, Wang Zhi-Guang, Sun Jian-Rong, Yao Cun-Feng, Chang Hai-Long, Pang Li-Long, Zhu Ya-Bin, Cui Ming-Huan, Zhang Hong-Peng, Li Yuan-Fei, Wang Ji, Zhu Hui-Ping, Song Peng, Wang Dong. Spectra study of He-irradiation induced defects in 6H-SiC. Acta Physica Sinica, 2014, 63(21): 216101. doi: 10.7498/aps.63.216101
[10]	Tong Ai-Hong, Feng Guo-Qiang, Deng Yong-Ju. Dependence of nonsequential double ionization of He on intensity ratio of orthogonal two-color field. Acta Physica Sinica, 2012, 61(9): 093303. doi: 10.7498/aps.61.093303
[11]	Liu Wang, Wu Qi-Qi, Chen Shun-Li, Zhu Jing-Jun, An Zhu, Wang Yuan. Helium effect on the stability of the interface of Cu/W nanomultilayer. Acta Physica Sinica, 2012, 61(17): 176802. doi: 10.7498/aps.61.176802
[12]	Zhang Yong, Zhang Chong-Hong, Zhou Li-Hong, Li Bing-Sheng, Yang Yi-Tao. Study on nanohardness of helium-implanted 4H-SiC. Acta Physica Sinica, 2010, 59(6): 4130-4135. doi: 10.7498/aps.59.4130
[13]	Wang Hai-Yan, Zhu Wen-Jun, Deng Xiao-Liang, Song Zhen-Fei, Chen Xiang-Rong. Plastic deformation of helium bubble and void in aluminum under shock loading. Acta Physica Sinica, 2009, 58(2): 1154-1160. doi: 10.7498/aps.58.1154
[14]	Wang Hai-Yan, Zhu Wen-Jun, Song Zhen-Fei, Liu Shao-Jun, Chen Xiang-Rong, He Hong-Liang. The influence of helium bubble on the elastic properties of aluminum. Acta Physica Sinica, 2008, 57(6): 3703-3708. doi: 10.7498/aps.57.3703
[15]	Zhou Xiao-Hua, Zhang Shao-Guang, Yang Ji-Qing, Qu Xue-Min, Liu Yuan-Sheng, Wang Si-Gang. Some new limiting vesicles and typical phase transforms and abruptions processes studied using the spontaneous-curvature model. Acta Physica Sinica, 2007, 56(10): 6137-6142. doi: 10.7498/aps.56.6137
[16]	Zheng Hui. A new inversion simulation method for analyzing experimental data of helium bubble growth in materials. Acta Physica Sinica, 2007, 56(1): 389-394. doi: 10.7498/aps.56.389
[17]	Cao Li-Xia, Wang Chong-Yu. Molecular dynamics simulation of fracture in α-iron. Acta Physica Sinica, 2007, 56(1): 413-422. doi: 10.7498/aps.56.413
[18]	Liu Yu-Xiao, Zhao Zhen-Hua, Wang Yong-Qiang, Chen Yu-Hong. Variational calculations and relativistic corrections to the nonrelativistic ground energies of the helium atom and the helium-like ions. Acta Physica Sinica, 2005, 54(6): 2620-2624. doi: 10.7498/aps.54.2620
[19]	ZHANG CHONG-HONG, CHEN KE-QIN, WANG YIN-SHU, SUN JI-GUANG. THE FORMATION OF HELIUM BUBBLES IN 316L STAINLESS STEEL IRRADIATED WITH 2.5 MeV He+ IONS. Acta Physica Sinica, 1997, 46(9): 1774-1781. doi: 10.7498/aps.46.1774
[20]	RAN QI-ZE. A SIMPLE AND RELIABLE HELIUM LEVEL INDICATOR. Acta Physica Sinica, 1976, 25(3): 270-270. doi: 10.7498/aps.25.270

Catalog

Vol. 70, Issue 7 - 2021-04-05

Metrics

Abstract views: 5381
PDF Downloads: 93
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板