-
Kelvin-Helmholtz instability is the basic physical process of fluids and plasmas. It is widely present in natural, astrophysical, and high energy density physical phenomena. With the construction of strong laser facilities, the research on high energy density physics has gained new impetus. However, in recent years the magnetized Kelvin-Helmholtz instability was rarely studied experimentally. In this work, we propose a new experimental scheme, in which a long-pulsed nanosecond laser beam is generated by a domestic starlight III laser facility. The whole target consists of two parts: the upper part that is the CH modulation layer with lower density, and the lower part that is the Al modulation layer with higher density. The laser beam is injected from one side of the CH modulation layer and generates a CH plasma outflow at the back of the target. During the transmission of the CH plasma outflow, the Al modulation layer is radiated and ionized, which makes the Al modulation layer generate an Al plasma outflow. The interaction between the Al plasma outflow and the CH plasma outflow produces a velocity shear layer, and then Kelvin-Helmholtz instability will gradually form near the Al modulation layer. In this paper, the open-source FLASH simulation program is used to conduct a two-dimensional numerical simulation of the Kelvin-Helmholtz instability generated by the laser-driven modulation target. We use the FLASH code, which is an adaptive mesh refinement program, developed by the Flash Center at the University of Chicago, and is well-known in astrophysics and space geophysics, to create a reference to the magnetohydrodynamic solution in our experiment. At present, this code introduces a complete high-energy-density physical modeling module, which is especially suitable for simulating intense laser ablation experiments. The equation of state and opacity tables of targets are based on the IONMIX4 database. The evolution of Kelvin-Helmholtz vortices, separately, in the Biermann self-generated magnetic field, the external magnetic field, and no magnetic field are investigated and compared with each other. It is found that the self-generated magnetic field hardly changes the morphology of the Kelvin-Helmholtz vortex during the evolution of Kelvin-Helmholtz instability. The external magnetic field parallel to the fluid direction can stabilize the shear flow. The magnetic field mainly stabilizes the long wave disturbance. The study results in this work can provide theoretical guidance for the next step of the Kelvin-Helmholtz experiment under a strong magnetic environment in the high energy density laser facility.
-
Keywords:
- magnetic field /
- Kelvin-Helmholtz instability /
- high energy density /
- laser
[1] Li X, Zhang J, Yang S, Hou Y, Erdelyi R 2018 Sci. Rep. 8 8136
Google Scholar
[2] Steinbusch B, Gibbon P, Sydora R D 2016 Phys. Plasmas 23 052119
Google Scholar
[3] Price D J, Rosswog S 2006 Science 312 719
Google Scholar
[4] Kiuchi K, Cerdá-Durán P, Kyutoku K, Sekiguchi Y, Shibata M 2015 Phys. Rev. D 92 124034
Google Scholar
[5] Foullon C, Verwichte E, Nakariakov V M, Nykyri K, Farrugia C J 2011 Astrophys. J. Lett. 729 L8
Google Scholar
[6] Li X, Narayan R 2004 Astrophys. J. 601 414
Google Scholar
[7] Yuan D, Shen Y, Liu Y, Li H, Feng X, Keppens R 2019 Astrophys. J. Lett. 884 L51
Google Scholar
[8] Ershkovich A I 1980 Space Sci. Rev. 25 3
Google Scholar
[9] Dittrich T R, Hammel B A, Keane C J, McEachern R, Turner R E, Haan S W, Suter L J 1994 Phys. Rev. Lett. 73 2324
Google Scholar
[10] Hammel B A, Haan S W, Clark D S, Edwards M J, Langer S H, Marinak M M, Patel M V, Salmonson J D, Scott H A 2010 High Energy Dens. Phys. 6 171
Google Scholar
[11] Clark D S, Haan S W, Cook A W, Edwards M J, Hammel B A, Koning J M, Marinak M M 2011 Phys. Plasmas 18 082701
Google Scholar
[12] Zhou Y, Remington B A, Robey H F, Cook A W, Glendinning S G, Dimits A, Buckingham A C, Zimmerman G B, Burke E W, Peyser T A, Cabot W, Eliason D 2003 Phys. Plasmas 10 1883
Google Scholar
[13] Zhou Y 2017 Phys. Rep. 720-722 1
Google Scholar
[14] Chandrasekhar S 1961 Hydrodynamic and Hydromagnetic Stability (Oxford: Clarendon Press) pp481−512
[15] 范征锋, 叶文华, 孙彦乾, 郑炳松, 李英骏, 王立锋 2009 58 6381
Google Scholar
Fan Z F, Ye W H, Sun Y Q, Zheng B S, Li Y J, Wang L F 2009 Acta Phys. Sin. 58 6381
Google Scholar
[16] 范征锋, 叶文华, 李英骏, 王立锋 2009 58 4787
Google Scholar
Fan Z F, Ye W H, Li Y J, Wang L F 2009 Acta Phys. Sin. 58 4787
Google Scholar
[17] Mak J, Griffiths S D, Hughes D W 2017 Phys. Rev. Fluid 2 113701
Google Scholar
[18] Liu Y, Chen Z H, Zhang H H, Lin Z Y 2018 Phys. Fluids 30 044102
Google Scholar
[19] Harding E C, Hansen J F, Hurricane O A, Drake R P, Robey H F, Kuranz C, Gillespie R S 2009 Phys. Rev. Lett. 103 045005
Google Scholar
[20] Wan W C, Malamud G, Shimony A, Stefano C A, Trantham M R, Klein S R, Drake R P 2015 Phys. Rev. Lett. 115 145001
Google Scholar
[21] Wan W C, Malamud G, Shimony A, Di Stefano C A, Trantham M R, Klein S R, Kuranz C C 2017 Phys. Plasmas 24 055705
Google Scholar
[22] Sun W, Zhong J, Zhang S, Tong B W, Wang L F, Zhao K G, Liu J Y, Han B, Zhu B J, Yuan D W, Yuan X X, Zhang Z, Li Y T, Zhang Q, Peng J M, Wang J Z, Ping Y L, Xing C Q, Wei H G, Liang G Y, Xie Z Y, Wang C, Zhao G, Zhang J 2019 High Energy Dens. Phys. 31 47
Google Scholar
[23] Fryxell B, Olson K, Ricker P, Timmes F X, Zingale M, Lamb D Q, Macneice P, Rosner R, Truran J W, Tufo H M 2000 Astrophys. J. Suppl. Ser. 131 273
Google Scholar
[24] Macfarlane J J 1989 Comput. Phys. Commun. 56 259
Google Scholar
[25] Rutter E M, Grosskopf M J, Malamud G, Kuranz C C, Harding E C, Keiter P A, Drake R P 2013 High Energy Dens. Phys. 9 148
Google Scholar
[26] Farmer W A, Koning J M, Strozzi D J, Hinkel D E, Berzak Hopkins L F, Jones O S, Rosen M D 2017 Phys. Plasmas 24 052703
Google Scholar
[27] Woolsey N C, Courtois C, Dendy R O 2004 Plasma Phys. Controlled Fusion 46 B397
Google Scholar
-
图 1 利用激光驱动调制靶产生KHI的实验方案(虚线框是模拟区域)
Figure 1. Experimental scheme for KHI using the laser-driven modulation targets. The dashed line box is the simulation domain.
图 2 无磁场时不同时刻的电子密度分布图 (a) 20 ns; (b) 40 ns; (c) 60 ns; (d) 80 ns
Figure 2. Snapshots of the electron density distribution at different times without magnetic field: (a) 20 ns; (b) 40 ns; (c) 60 ns; (d) 80 ns.
图 3 x方向外加0.4 T磁场时不同时刻的电子密度分布图 (a) 0 ns; (b) 40 ns; (c) 80 ns; (d) 120 ns
Figure 3. Snapshots of the electron density distribution at different times with 0.4 T in x direction: (a) 0 ns; (b) 40 ns; (c) 80 ns; (d) 120 ns.
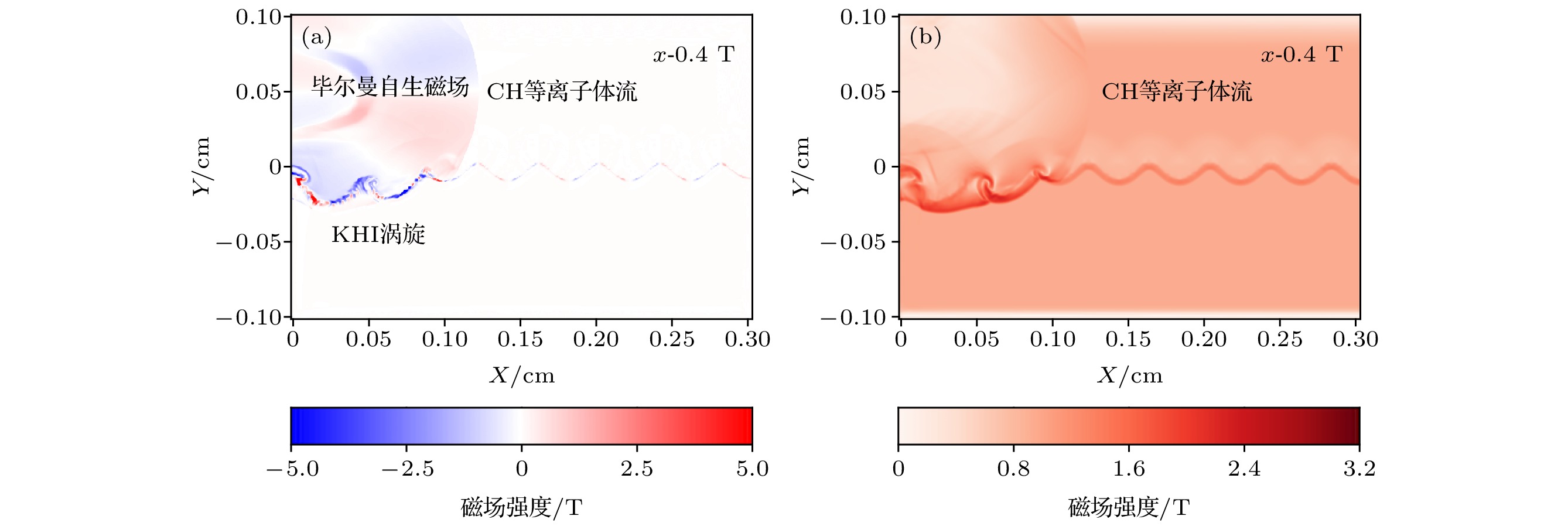
图 4 (a) 考虑毕尔曼自生磁场, 在120 ns时毕尔曼自生磁场强度的分布情况; (b)忽略毕尔曼自生磁场, 在120 ns时外加磁场在模拟平面的分布情况
Figure 4. (a) Considering the Biermann self-generated magnetic field, the distribution of the Bierman self-generated magnetic field strength at 120 ns; (b) ignoring the Bierman self-generated magnetic field, the distribution of the applied magnetic field in the simulated plane at 120 ns.
图 5 x方向外加0.4 T磁场时不同时刻外加磁场的分布情况 (a)静态参考图像(0 ns); (b) 40 ns的磁场分布图像; (c) 80 ns的磁场分布图像; (d) 120 ns的磁场分布图像
Figure 5. Snapshots of the magnetic field distribution at different delay times with 0.4 T in x direction: (a) Reference image (0 ns); (b) 40 ns. (c) 80 ns; (d) 120 ns
图 6 (a) 120 ns时磁压力的分布情况; (b) 120 ns的磁张力的分布情况
Figure 6. (a) Distribution of magnetic pressure at 120 ns; (b) distribution of magnetic tension at 120 ns.
图 7 (a) 有无外加磁场的情况下, KHI涡旋的生长情况; (b) x方向外加0.4 T磁场, 初始扰动波长不同时, KHI涡旋的生长情况
Figure 7. (a) Growth of the KHI vortex with or without an external magnetic field; (b) the growth of the KHI vortex when a 0.4 T magnetic field is applied in the x direction and the initial disturbance wavelength is different.
-
[1] Li X, Zhang J, Yang S, Hou Y, Erdelyi R 2018 Sci. Rep. 8 8136
Google Scholar
[2] Steinbusch B, Gibbon P, Sydora R D 2016 Phys. Plasmas 23 052119
Google Scholar
[3] Price D J, Rosswog S 2006 Science 312 719
Google Scholar
[4] Kiuchi K, Cerdá-Durán P, Kyutoku K, Sekiguchi Y, Shibata M 2015 Phys. Rev. D 92 124034
Google Scholar
[5] Foullon C, Verwichte E, Nakariakov V M, Nykyri K, Farrugia C J 2011 Astrophys. J. Lett. 729 L8
Google Scholar
[6] Li X, Narayan R 2004 Astrophys. J. 601 414
Google Scholar
[7] Yuan D, Shen Y, Liu Y, Li H, Feng X, Keppens R 2019 Astrophys. J. Lett. 884 L51
Google Scholar
[8] Ershkovich A I 1980 Space Sci. Rev. 25 3
Google Scholar
[9] Dittrich T R, Hammel B A, Keane C J, McEachern R, Turner R E, Haan S W, Suter L J 1994 Phys. Rev. Lett. 73 2324
Google Scholar
[10] Hammel B A, Haan S W, Clark D S, Edwards M J, Langer S H, Marinak M M, Patel M V, Salmonson J D, Scott H A 2010 High Energy Dens. Phys. 6 171
Google Scholar
[11] Clark D S, Haan S W, Cook A W, Edwards M J, Hammel B A, Koning J M, Marinak M M 2011 Phys. Plasmas 18 082701
Google Scholar
[12] Zhou Y, Remington B A, Robey H F, Cook A W, Glendinning S G, Dimits A, Buckingham A C, Zimmerman G B, Burke E W, Peyser T A, Cabot W, Eliason D 2003 Phys. Plasmas 10 1883
Google Scholar
[13] Zhou Y 2017 Phys. Rep. 720-722 1
Google Scholar
[14] Chandrasekhar S 1961 Hydrodynamic and Hydromagnetic Stability (Oxford: Clarendon Press) pp481−512
[15] 范征锋, 叶文华, 孙彦乾, 郑炳松, 李英骏, 王立锋 2009 58 6381
Google Scholar
Fan Z F, Ye W H, Sun Y Q, Zheng B S, Li Y J, Wang L F 2009 Acta Phys. Sin. 58 6381
Google Scholar
[16] 范征锋, 叶文华, 李英骏, 王立锋 2009 58 4787
Google Scholar
Fan Z F, Ye W H, Li Y J, Wang L F 2009 Acta Phys. Sin. 58 4787
Google Scholar
[17] Mak J, Griffiths S D, Hughes D W 2017 Phys. Rev. Fluid 2 113701
Google Scholar
[18] Liu Y, Chen Z H, Zhang H H, Lin Z Y 2018 Phys. Fluids 30 044102
Google Scholar
[19] Harding E C, Hansen J F, Hurricane O A, Drake R P, Robey H F, Kuranz C, Gillespie R S 2009 Phys. Rev. Lett. 103 045005
Google Scholar
[20] Wan W C, Malamud G, Shimony A, Stefano C A, Trantham M R, Klein S R, Drake R P 2015 Phys. Rev. Lett. 115 145001
Google Scholar
[21] Wan W C, Malamud G, Shimony A, Di Stefano C A, Trantham M R, Klein S R, Kuranz C C 2017 Phys. Plasmas 24 055705
Google Scholar
[22] Sun W, Zhong J, Zhang S, Tong B W, Wang L F, Zhao K G, Liu J Y, Han B, Zhu B J, Yuan D W, Yuan X X, Zhang Z, Li Y T, Zhang Q, Peng J M, Wang J Z, Ping Y L, Xing C Q, Wei H G, Liang G Y, Xie Z Y, Wang C, Zhao G, Zhang J 2019 High Energy Dens. Phys. 31 47
Google Scholar
[23] Fryxell B, Olson K, Ricker P, Timmes F X, Zingale M, Lamb D Q, Macneice P, Rosner R, Truran J W, Tufo H M 2000 Astrophys. J. Suppl. Ser. 131 273
Google Scholar
[24] Macfarlane J J 1989 Comput. Phys. Commun. 56 259
Google Scholar
[25] Rutter E M, Grosskopf M J, Malamud G, Kuranz C C, Harding E C, Keiter P A, Drake R P 2013 High Energy Dens. Phys. 9 148
Google Scholar
[26] Farmer W A, Koning J M, Strozzi D J, Hinkel D E, Berzak Hopkins L F, Jones O S, Rosen M D 2017 Phys. Plasmas 24 052703
Google Scholar
[27] Woolsey N C, Courtois C, Dendy R O 2004 Plasma Phys. Controlled Fusion 46 B397
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 5607
- PDF Downloads: 89
- Cited By: 0
