中高能重离子碰撞中的电磁场效应和手征反常现象

赵新丽; 马国亮; 马余刚

doi:10.7498/aps.72.20230245

摘要

重离子碰撞可以产生极强的电磁场和高温高密量子色动力学(QCD)物质, 诱导很多重要手征反常现象, 例如手征磁效应和手征磁波. 本文围绕手征反常现象中的诸多物理要素, 详细介绍包括相对论重离子碰撞中不同碰撞系统和能量下的电磁场特性、同质异位素碰撞中寻找手征磁效应、手征磁波特性、中低能重离子碰撞中磁场效应等一系列与电磁场和手征反常现象相关的理论研究成果. 相关研究有助于实验中寻找强相互作用中的电荷宇称($\cal{CP}$)破缺的证据, 加深对QCD真空涨落和宇宙中正反物质不对称问题的理解.

关键词:

Abstract

Heavy-ion collisions can produce high-temperature and high-density quantum chromodynamics (QCD) matter under extremely strong electromagnetic fields, which triggers off many important anomalous chiral phenomena, such as the chiral magnetic effect and chiral magnetic wave. The anomalous chiral phenomena can help to find the evidence of $\cal{CP}$ symmetry breaking in the strong interaction, deepen the understanding of the QCD vacuum fluctuations, and disclose the mystery of asymmetry of antimatter-matter in the universe. In this paper, firstly, the magnetic fields are investigated for small and large colliding systems at relativistic heavy ion collider (RHIC) and large hadron collider (LHC). These studies indicate that collision energy and initial nucleon structure have significant effects on magnetic fields. And, the lifetimes of magnetic field in different media are very different in heavy-ion collisions. Then, in order to study the chiral magnetic effect, some experimental observables are studied by using a multi-phase transport model without or with different strengths of the chiral magnetic effect. For small systems, if QGP exists, the chiral magnetic effect could be observed in the peripheral collisions. For isobaric collisions, the correlators with respect to the spectator plane can imply a much cleaner signal of chiral magnetic effect than that with respect to the participant plane. Our results support that the strength of chiral magnetic effect may be absent or small in isobaric collisions. Next, some new strategies are applied to study the chiral magnetic wave. Moreover, a novel mechanism for the electric quadrupole moment can also explain the charge-dependent elliptic flow of pions generated by the chiral magnetic wave. In addition, some interesting phenomena also occur, owing to the magnetic field in heavy-ion collisions at intermediate energy. The directed flow and elliptic flow of photons have no effect on magnetic field at $p_{\rm T}<25$ GeV. However, because of the magnetic field, the directed flow of photons decreases and the elliptic flow of photons increases at $p_{\rm T}>25$ GeV. Besides, the magnetic field has a significant effect on giant dipole resonance, i.e. the magnetic field increases the angular momentum and enhances some observables of the giant dipole resonance spectrum. In conclusion, magnetic field plays a key role in heavy-ion collisions at both high energy and intermediate energy. It provides an unprecedented opportunity for studying the microscopic laws of nuclear physics. However, there are still many unsolved problems that need further studying in the future.

Keywords:

作者及机构信息

1.
复旦大学现代物理研究所, 核物理与离子束应用教育部重点实验室, 上海　200433

2.
复旦大学, 理论物理专款上海核物理理论研究中心, 上海　200438

通信作者: 马国亮, glma@fudan.edu.cn ; 马余刚, mayugang@fudan.edu.cn

基金项目: 国家重点研发计划(批准号: 2022YFA1604900)、国家自然科学基金(批准号: 12147101, 11890714, 11835002, 11961131011, 11421505, 12105054)、中国科学院战略优先研究计划(批准号: XDB34030000)和广东省基础与应用基础研究重大项目(批准号: 2020B0301030008)资助的课题

Authors and contacts

1.
Key Laboratory of Nuclear Physics and Ion-beam Application, Ministry of Education, Institute of Modern Physics, Fudan University, Shanghai 200433, China

2.
Shanghai Research Center for Theoretical Nuclear Physics, National Natural Science Foundation of China, Fudan University, Shanghai 200438, China

Corresponding author: Ma Guo-Liang, glma@fudan.edu.cn ; Ma Yu-Gang, mayugang@fudan.edu.cn

Funds: Project supported by the National Key R&D Program of China (Grant No. 2022YFA1604900), the National Natural Science Foundation of China (Grant Nos. 12147101, 11890714, 11835002, 11961131011, 11421505, 12105054), the Strategic Priority Research Program of Chinese Academy of Sciences (Grant No. XDB34030000), and the Major Project of Basic and Applied Basic Research of Guangdong Province, China (Grant No. 2020B0301030008)

文章全文 : translate this paragraph

参考文献

[1]	Gross D J, Wilczek F 1973 Phys. Rev. Lett. 30 1343 Google Scholar
[2]	Politzer H D 1973 Phys. Rev. Lett. 30 1346 Google Scholar
[3]	Adams J,Aggarwal M M, Ahammed Z, et al. (STAR Collaboration). 2005 Nucl. Phys. A 757 102 Google Scholar
[4]	Adcox K, Adler S S, Afanasiev S, et al. (PHENIX Collaboration). 2005 Nucl. Phys. A 757 184 Google Scholar
[5]	Aamodt K, Quintana A A, Achenbach R, et al. (ALICE Collaboration). 2008 JINST 3 S08002 Google Scholar
[6]	Bzdak A, Esumi S, Koch V, Liao J, Stephanov M, Xu N 2020 Phys. Rep. 853 1 Google Scholar
[7]	Luo X, Xu N 2017 Nucl. Sci. Tech. 28 112 Google Scholar
[8]	Xu J, Liao J, Gyulassy M 2015 Chin. Phys. Lett. 32 092501 Google Scholar
[9]	Siemens P J, Rasmussen J O 1979 Phys. Rev. Lett. 42 880 Google Scholar
[10]	Kolb P F, Sollfrank J, Heinz U W 2000 Phys. Rev. C 62 054909 Google Scholar
[11]	Teaney D, Lauret J, Shuryak E V 2001 Phys. Rev. Lett. 86 4783 Google Scholar
[12]	Song H, Heinz U W 2008 Phys. Rev. C 77 064901 Google Scholar
[13]	Jeon S, Heinz U 2015 Int. J. Mod. Phys. E 24 1530010 Google Scholar
[14]	Shen C, Yan L 2020 Nucl. Sci. Tech. 31 122 Google Scholar
[15]	Lao H L, Liu F H, Li B C, Duan M Y, Lacey R A 2018 Nucl. Sci. Tech. 29 164 Google Scholar
[16]	Waqas M, Liu F H, Li L L, Alfanda H M 2020 Nucl. Sci. Tech. 31 109 Google Scholar
[17]	Poskanzer A M, Voloshin S A 1998 Phys. Rev. C 58 1671 Google Scholar
[18]	Gale C, Jeon S, Schenke B 2013 Int. J. Mod. Phys. A 28 1340011 Google Scholar
[19]	Alver B, Roland G 2010 Phys. Rev. C 81 054905 Google Scholar
[20]	Ma G L, Wang X N 2011 Phys. Rev. Lett. 106 162301 Google Scholar
[21]	Ma L, Ma G L, Ma Y G 2016 Phys. Rev. C 94 044915 Google Scholar
[22]	Lee T D, Yang C N 1956 Phys. Rev. 104 254 Google Scholar
[23]	Christenson J H, Cronin J W, Fitch V L, Turlay R 1964 Phys. Rev. Lett. 13 138 Google Scholar
[24]	Skokov V, Illarionov A Y, Toneev V 2009 Int. J. Mod. Phys. A 24 5925 Google Scholar
[25]	Bzdak A, Skokov V 2012 Phys. Lett. B 710 171 Google Scholar
[26]	Deng W T, Huang X G 2012 Phys. Rev. C 85 044907 Google Scholar
[27]	Hattori K, Huang X G 2017 Nucl. Sci. Tech. 28 26 Google Scholar
[28]	Rojas H P, Martinez A P, Cuesta H J M 2004 Chin. Phys. Lett. 21 2117 Google Scholar
[29]	Kharzeev D 2006 Phys. Lett. B 633 260 Google Scholar
[30]	Kharzeev D, Zhitnitsky A 2007 Nucl. Phys. A 797 67 Google Scholar
[31]	Kharzeev D E, McLerran L D, Warringa H J 2008 Nucl. Phys. A 803 227 Google Scholar
[32]	Fukushima F, Kharzeev D E, Warringa H J 2008 Phys. Rev. D 78 074033 Google Scholar
[33]	Son D T, Zhitnitsky A R 2004 Phys. Rev. D 70 074018 Google Scholar
[34]	Metlitski M A, Zhitnitsky A R 2005 Phys. Rev. D 72 045011 Google Scholar
[35]	Kharzeev D E, Liao J F, Voloshin S A, Wang G 2016 Prog. Part. Nucl. Phys. 88 1 Google Scholar
[36]	Kharzeev D E, Yee H U 2011 Phys. Rev. D 83 085007 Google Scholar
[37]	罗晓丽, 高建华 2023 72 112503 Google Scholar Luo X L, Gao J H 2023 Acta Phys. Sin. 72 112503 Google Scholar
[38]	Bertsch G F, Gupta S D 1988 Phys. Rep. 160 189 Google Scholar
[39]	Maruyama T, Niita K, Iwamoto A 1996 Phys. Rev. C 53 297 Google Scholar
[40]	Lin Z W, Ko C M, Li B A, Zhang B, Pal S 2005 Phys. Rev. C 72 064901 Google Scholar
[41]	Zhao X L, Ma Y G, Ma G L 2018 Phys. Rev. C 97 024910 Google Scholar
[42]	Zhao X L, Ma G L, Ma Y G 2019 Phys. Rev. C 99 034903 Google Scholar
[43]	Deng W T, Huang X G, Ma G L, Wang G 2018 Phys. Rev. C 97 044901 Google Scholar
[44]	Cheng Y L, Zhang S, Ma Y G, Chen J H, Zhong C 2019 Phys. Rev. C 99 054906 Google Scholar
[45]	Chen Y, Sheng X L, Ma G L 2021 Nucl. Phys. A 1011 122199 Google Scholar
[46]	Zhong Y, Yang C B, Cai X, Feng S Q 2015 Chin. Phys. C 39 104105 Google Scholar
[47]	Kharzeev D E, Liao J F 2021 Nat. Rev. Phys. 3 55 Google Scholar
[48]	Huang X G 2016 Rept. Prog. Phys. 79 076302 Google Scholar
[49]	Gao J H, Ma G L, Pu S, Wang Q 2020 Nucl. Sci. Tech. 31 90 Google Scholar
[50]	Voloshin S A 2004 Phys. Rev. C 70 057901 Google Scholar
[51]	Abelev B I, Aggarwal M M, Ahammed Z, et al. [STAR]. 2009 Phys. Rev. Lett. 103 251601 Google Scholar
[52]	Abelev B I, Aggarwal M M, Ahammed Z, et al. 2010 Phys. Rev. C 81 054908 Google Scholar
[53]	Adamczyk L, Adkins J K, Agakishiev G, et al. [STAR]. 2013 Phys. Rev. C 88 064911 Google Scholar
[54]	Adamczyk L, Adkins J K, Agakishiev G, et al. [STAR]. 2014 Phys. Rev. Lett. 113 052302 Google Scholar
[55]	Abelev B, Adam J, Adamova D, et al. [ALICE]. 2013 Phys. Rev. Lett. 110 012301 Google Scholar
[56]	Lin Z W, Zheng L 2021 Nucl. Sci. Tech. 32 113 Google Scholar
[57]	Ma G L, Zhang B 2011 Phys. Lett. B 700 39 Google Scholar
[58]	Shou Q Y, Ma G L, Ma Y G 2014 Phys. Rev. C 90 047901 Google Scholar
[59]	Huang L, Ma C W, Ma G L 2018 Phys. Rev. C 97 034909 Google Scholar
[60]	Huang L, Nie M W, Ma G L 2020 Phys. Rev. C 101 024916 Google Scholar
[61]	Khachatryan V, Sirunyan A M, Tumasyan A, et al. [CMS]. 2017 Phys. Rev. Lett. 118 122301 Google Scholar
[62]	Zhang Z W, Cen X Z, Deng W T 2022 Chin. Phys. C 46 084103 Google Scholar
[63]	Bzdak A, Koch V, Liao J 2011 Phys. Rev. C 83 014905 Google Scholar
[64]	Liao J, Koch V, Bzdak A 2010 Phys. Rev. C 82 054902 Google Scholar
[65]	Schlichting S, Pratt S 2011 Phys. Rev. C 83 014913 Google Scholar
[66]	Wang F 2010 Phys. Rev. C 81 064902 Google Scholar
[67]	Zhao J [STAR] 2021 Nucl. Phys. A 1005 121766 Google Scholar
[68]	Zhao J, Wang F 2019 Prog. Part. Nucl. Phys. 107 200 Google Scholar
[69]	Wang F 2022 Acta Phys. Polon. Supp. 16 15
[70]	Li W, Wang G 2020 Ann. Rev. Nucl. Part. Sci. 70 293 Google Scholar
[71]	Voloshin S A 2010 Phys. Rev. Lett. 105 172301 Google Scholar
[72]	Deng W T, Huang X G, Ma G L, Wang G 2016 Phys. Rev. C 94 041901 Google Scholar
[73]	Adam J, Adamczyk L, Adams J R, et al. [STAR]. 2021 Nucl. Sci. Tech. 32 48 Google Scholar
[74]	Abdallah M, Aboona B E, Adam J, et al. [STAR]. 2022 Phys. Rev. C 105 014901 Google Scholar
[75]	Xu H J, Li H, Wang X, Shen C, Wang F 2021 Phys. Lett. B 819 136453 Google Scholar
[76]	Xu H J, Zhao W, Li H, Zhou Y, Chen L W, Wang F 2021 arXiv: 2111.14812 [nucl-th]
[77]	Zhang C, Jia J 2022 Phys. Rev. Lett. 128 022301 Google Scholar
[78]	Jia J, Zhang C J 2023 Phys. Rev. C 107 L021901 Google Scholar
[79]	Jia J 2022 Phys. Rev. C 105 014905 Google Scholar
[80]	Jia J 2022 Phys. Rev. C 105 044905 Google Scholar
[81]	Zhao X L, Ma G L 2022 Phys. Rev. C 106 034909 Google Scholar
[82]	Kharzeev D E, Liao J, Shi S 2022 Phys. Rev. C 106 L051903Google Scholar
[83]	Li F, Ma Y G, Zhang S, Ma G L, Shou Q, Shou Q Y 2022 Phys. Rev. C 106 014906 Google Scholar
[84]	Wang F Q, Zhao J 2018 Nucl. Sci. Tech. 29 179 Google Scholar
[85]	Xu H J, Zhao J, Wang X, Li H, Lin Z W, Shen C, Wang F 2018 Chin. Phys. C 42 084103 Google Scholar
[86]	Choudhury S, Dong X, Drachenberg J, et al. 2022 Chin. Phys. C 46 014101 Google Scholar
[87]	Tang A H 2020 Chin. Phys. C 44 054101 Google Scholar
[88]	Liang G R, Liao H F, Lin S, Yan Li, Li M 2020 Chin. Phys. C 44 094103 Google Scholar
[89]	Chen B X, Feng S Q 2020 Chin. Phys. C 44 024104 Google Scholar
[90]	Feng S Q, Pei L, Sun F, Zhong Y, Yin Z B 2018 Chin. Phys. C 42 054102 Google Scholar
[91]	Jiang Y, Shi S, Yin Y, Liao J 2018 Chin. Phys. C 42 011001 Google Scholar
[92]	Yee H U, Yin Y 2014 Phys. Rev. C 89 044909 Google Scholar
[93]	Taghavi S F, Wiedemann U A 2015 Phys. Rev. C 91 024902 Google Scholar
[94]	Hongo M, Hirono Y, Hirano T 2017 Phys. Lett. B 775 266 Google Scholar
[95]	Adamczyk L, Adkins J K, Agakishiev G, et al. [STAR]. 2015 Phys. Rev. Lett. 114 252302 Google Scholar
[96]	Adam J, Adamova D, Aggarwal M M, et al. [ALICE]. 2016 Phys. Rev. C 93 044903 Google Scholar
[97]	Ma G L 2014 Phys. Lett. B 735 383 Google Scholar
[98]	Zhao X L, Ma G L, Ma Y G 2019 Phys. Lett. B 792 413 Google Scholar
[99]	Wang C Z, Wu W Y, Shou Q Y, Ma G L, Ma Y G, Zhang S 2021 Phys. Lett. B 820 136580 Google Scholar
[100]	Wu W Y, Shou Q Y, Christakoglou P, Das P, Haque M R, Ma G L, Ma Y G, Mohanty B, Wang C Z, Zhang S, Zhao J 2023 Phys. Rev. C 107 L031902 Google Scholar
[101]	Shen D Y, Chen J H, Ma G L, Ma Y G, Shou Q Y, Zhang S, Zhong C 2019 Phys. Rev. C 100 064907 Google Scholar
[102]	Deng X G, Ma Y G 2018 Eur. Phys. J. A 54 204 Google Scholar
[103]	Cao Y T, Deng X G, Ma Y G 2022 Phys. Rev. C 106 014611 Google Scholar
[104]	阮丽娟, 许长补, 杨驰 2023 72 112401 Google Scholar Ruan L J, Xu Z B, Yang C 2023 Acta Phys. Sin. 72 112401 Google Scholar
[105]	寿齐烨, 赵杰, 徐浩洁, 李威, 王钢, 唐爱洪, 王福强 2023 72 112504 Google Scholar Shou Q Y, Zhao J, Xu H J, Li W, Wang G, Tang A H, Wang F Q 2023 Acta Phys. Sin. 72 112504 Google Scholar
[106]	高建华, 盛欣力, 王群, 庄鹏飞 2023 72 112501 Google Scholar Gao J H, Sheng X L, Wang Q, Zhuang P F 2023 Acta Phys. Sin. 72 112501 Google Scholar
[107]	浦实, 黄旭光 2023 72 071202 Google Scholar Pu S, Huang X G 2023 Acta Phys. Sin. 72 071202 Google Scholar

施引文献

图 1 自然界中的磁场强度

Fig. 1. Magnetic field strengths in nature

下载: 全尺寸图片幻灯片

图 2 LHC能量下(a) $ \rm Pb+Pb $碰撞和(b) ${\rm{p}}\rm+Pb$碰撞中的电磁场与碰撞参数b的关系

Fig. 2. Dependences of electromagnetic field on the impact parameter b for (a) $ \rm Pb+Pb $ collisions and (b) ${\rm{p}}\rm+Pb$ collisions at LHC energies

下载: 全尺寸图片幻灯片

图 3 RHIC能量下形变old case1情况下(a) ${\rm{Ru}}+{\rm{Ru}}$碰撞和(b)$ \rm Zr+Zr $碰撞中的电磁场与碰撞参数b的依赖关系; (c)两个同质异位素碰撞中磁场的相对差异与碰撞参数b的依赖关系

Fig. 3. Dependences of electromagnetic fields on the impact parameter b for (a) $ \rm Ru+Ru $ collisions and (b) $ \rm Zr+Zr $ collisions at RHIC energy. (c) Dependence of the relative ratio between the magnetic fields in the two isobaric collisions on the impact parameter b

下载: 全尺寸图片幻灯片

图 4 RHIC能量下不对称碰撞系统中磁场对碰撞参数b的依赖性

Fig. 4. Dependences of the magnetic field on impact parameter b for the asymmetric collisions at RHIC energy

下载: 全尺寸图片幻灯片

图 5 扩展的KMW模型给出的$ \rm Au+Au $碰撞中磁场强度随时间的演化

Fig. 5. Evolution of the magnetic fields in $ \rm Au+Au $ collisions using the extended KMW model

下载: 全尺寸图片幻灯片

图 6 CME示意图, 图片来自文献[35]

Fig. 6. Schematic diagram of CME, which is taken from Ref. [35]

下载: 全尺寸图片幻灯片

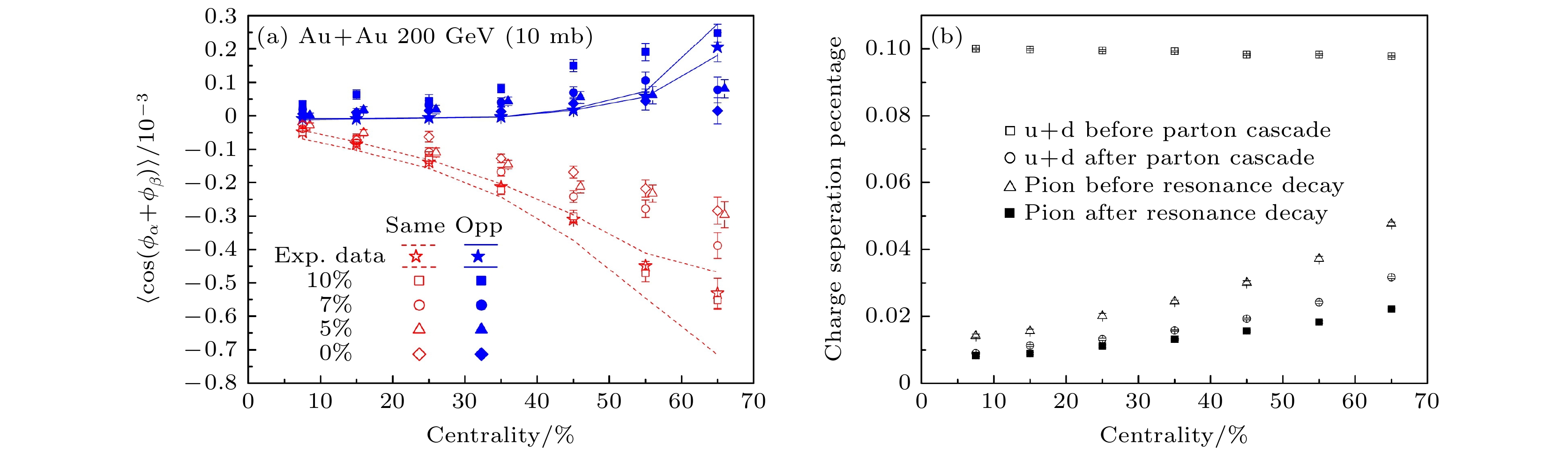
图 7 RHIC能量下$ \rm Au+Au $碰撞中, (a)不同初始电荷分离强度下电荷方位角关联与碰撞中心度的依赖关系, (b) 10%的初始电荷分离强度下, AMPT模型不同碰撞阶段的电荷分离百分比与碰撞中心度的依赖关系

Fig. 7. (a) Centrality dependence of $ \rm cos(\phi_{\alpha}+\phi_{\beta}) $ with the different fractions of charge separation in $ \rm Au+Au $ collisions at 200 GeV; (b) centrality dependence of charge separation percentage for different evolution stages in $ \rm Au+Au $ collisions at the RHIC energy, for 10% initial charge separation

下载: 全尺寸图片幻灯片

图 8 在RHIC能量下$ \rm Au+Au $碰撞中部分子相末态中CME粒子的分布, 其中(a) $ \sigma = 0 $ mb; (b)$ \sigma = 10 $ mb. (c) 10%的初始局域电荷分离强度下关联$ \rm cos(\phi_{\alpha}+\phi_{\beta}) $对碰撞中心度的依赖性

Fig. 8. Transverse spatial distribution of CME particles in the final partonic state in $ \rm Au+Au $ collisions at the RHIC energy, (a) for 0 mb and (b) for 10 mb. (c) Centrality dependence of the azimuthal correlation $ \rm cos(\phi_{\alpha}+\phi_{\beta}) $ with 10% of the initial local charge separation

下载: 全尺寸图片幻灯片

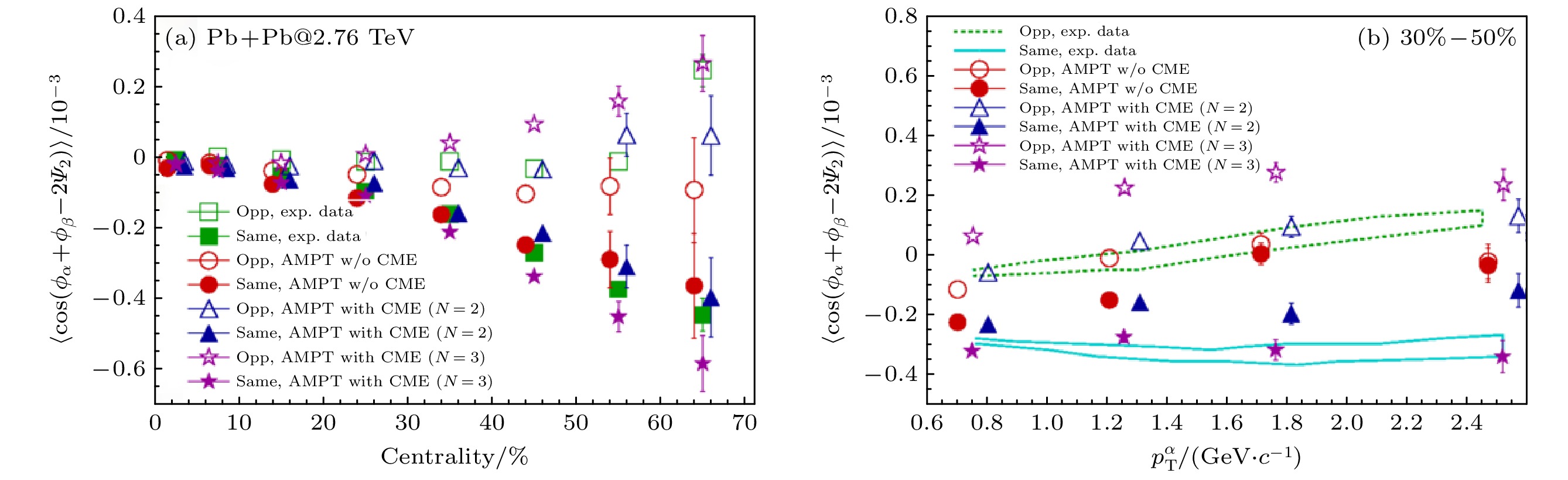
图 9 LHC能量下$ \rm Pb+Pb $碰撞中, (a)电荷方位角关联γ与碰撞中心度的依赖关系, 以及(b)30%—50%中心度下, 电荷方位角关联γ与横动量$ p_{\rm T} $的依赖关系

Fig. 9. (a) Centrality dependence of the charge azimuthal correlation γ in $ \rm Pb+Pb $ collisions at LHC energy; (b) transverse momentum $ p_{\rm T} $ dependence of the charge azimuthal correlation γ for 30%–50% centrality bin in $ \rm Pb+Pb $ collisions at the LHC energy

下载: 全尺寸图片幻灯片

图 10 RHIC能量下$ \rm Au+Au $碰撞30%—50%中心度中, 关联γ和$ \Delta\gamma $对初始电荷分离强度的依赖性

Fig. 10. Dependences of the correlations γ and $ \Delta\gamma $ on the initial charge separation percentage in the 30%–50% centrality bin of $ \rm Au+Au $ collisions at the RHIC energy

下载: 全尺寸图片幻灯片

图 11 (a) CMS合作组测量的在LHC能量下${\rm{p}}\rm+Pb$和$ \rm Pb+Pb $碰撞中三粒子方位角关联对$ N_{\rm track} $的依赖性^[61]; (b)不同能量和小系统碰撞下磁场方位角关联对$ N_{\rm track} $的依赖性

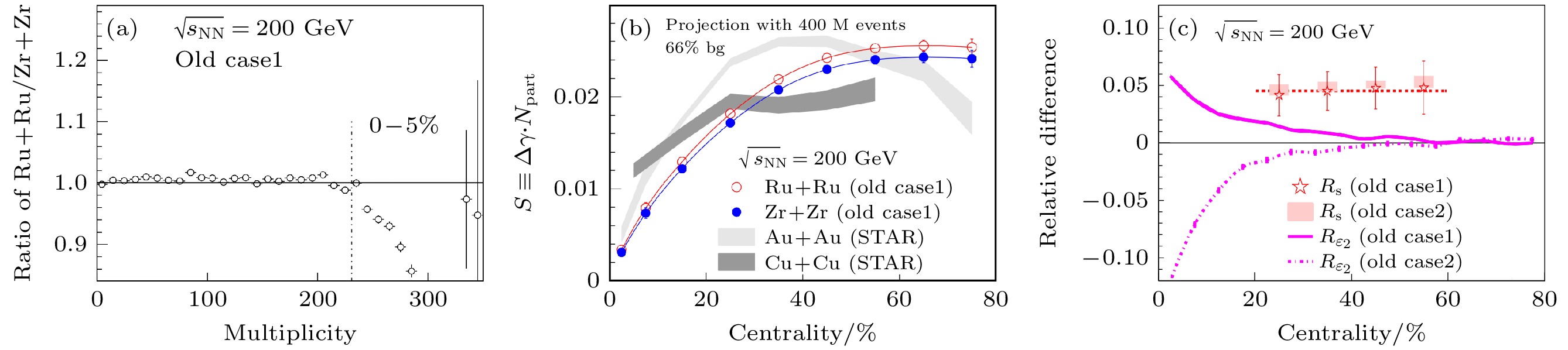
Fig. 11. (a) $ N_{\rm track} $ dependences of the three-particle azimuthal correlations in ${\rm{p}}\rm+Pb$ and $ \rm Pb+Pb $ collisions at the LHC energy measured by the CMS Collaboration; (b) $ N_{\rm track} $ dependences of correlation between the magnetic field and the event plane for small collisions at different energies

下载: 全尺寸图片幻灯片

图 12 RHIC能量的同质异位素碰撞中, (a) old case1的同质异位素碰撞中粒子分布比; (b)$ S=N_{\rm part}\times\Delta\gamma $与中心度的依赖关系; (c) S的相对比值与中心度的依赖关系

Fig. 12. (a) Ratio of multiplicity distribution between two isobar collisions for the deformation old case1; (b) centrality dependence of $ S=N_{\rm part}\times\Delta\gamma $; (c) centrality dependence of the relative ratio of S

下载: 全尺寸图片幻灯片

图 13 RHIC能量的同质异位素碰撞中, (a)方位角关联及其相对比值与中心度的依赖关系; (b)$ H=\gamma^{\rm CME}-\gamma^{\rm no\; CME} $及其相对比值与中心度的依赖关系; (c)初始电荷分离强度和末态电荷分离强度及其相对比值对碰撞参数b的依赖关系

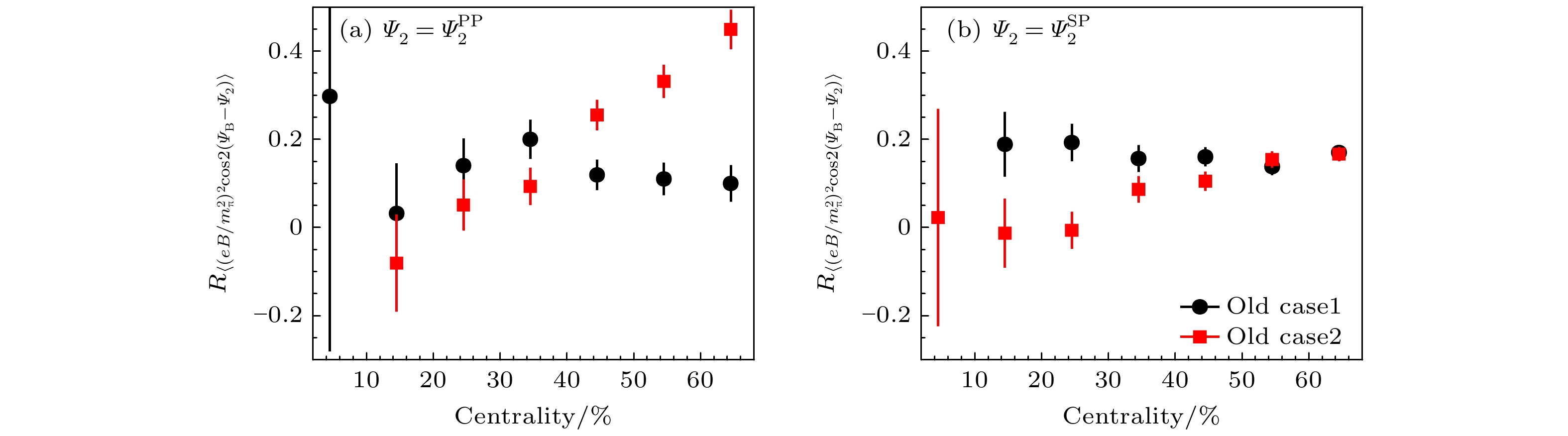
Fig. 13. In isobar collisions at the RHIC energy: (a) The centrality dependence of azimuthal correlation and its relative ratio; (b) the centrality dependence of $ H=\gamma^{\rm CME}-\gamma^{\rm no\; CME} $ and its relative ratio; (c) the impact parameter b dependence of initial charge separation strength and final state charge separation strength and its relative ratios

下载: 全尺寸图片幻灯片

图 14 RHIC能量的同质异位素碰撞中, (a)与$ \varPsi_{2}^{\rm PP} $有关的关联的相对比值与中心度的依赖关系; (b)与$ \varPsi_{2}^{\rm SP} $有关的关联的相对比值与中心度的依赖关系

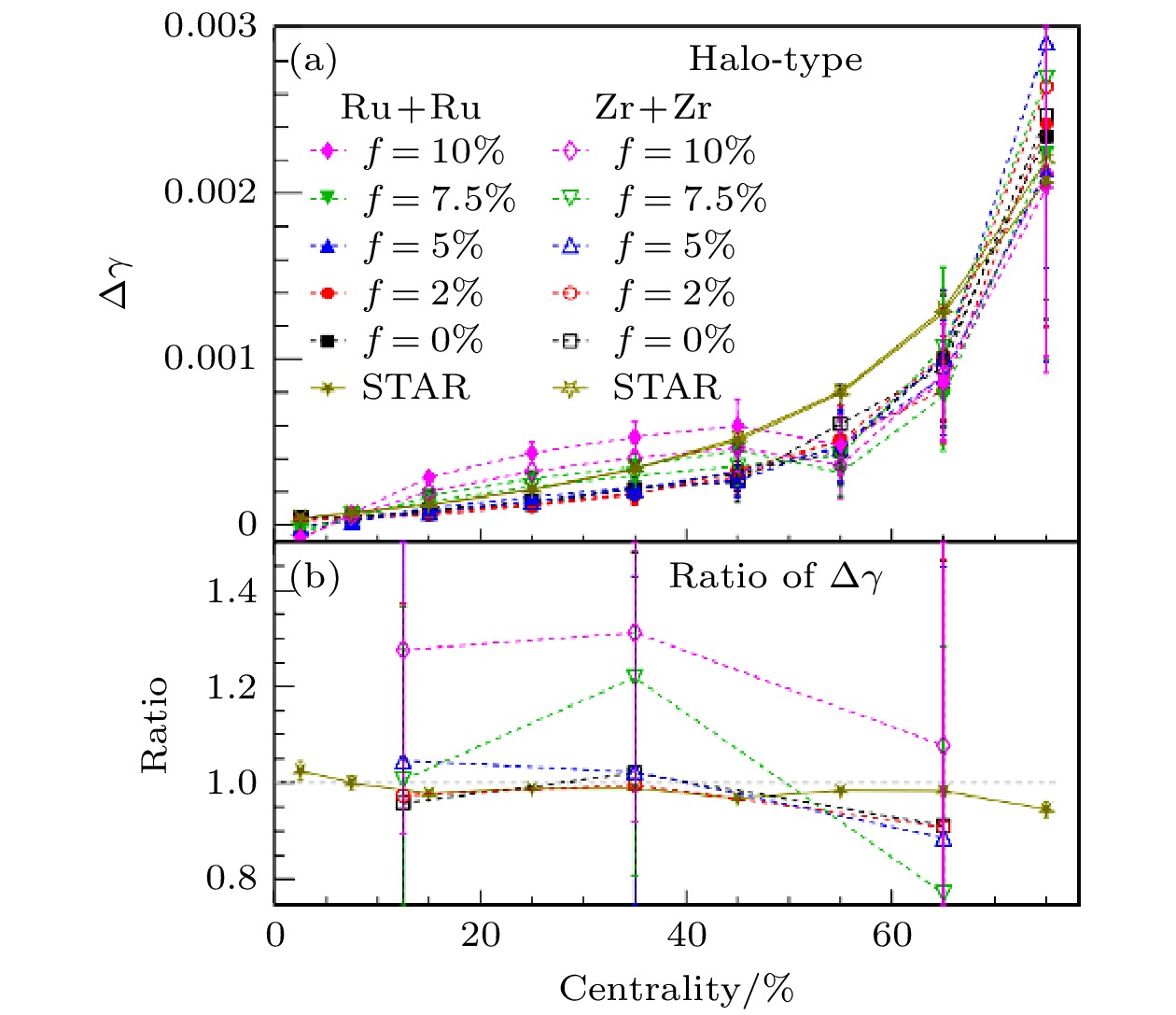
Fig. 14. In isobar collisions at the RHIC energy, (a) centrality dependence of the relative ratios of the correlations related to $ \varPsi_{2}^{\rm PP} $; (b) centrality dependence of the relative ratios of the correlations related to $ \varPsi_{2}^{\rm SP} $

下载: 全尺寸图片幻灯片

图 15 RHIC能量的同质异位素碰撞中不同电荷分离强度下, (a)带电粒子分布比值, (b)平均带电粒子比值与中心度的依赖关系以及(c)$ v_2 $比值与中心度的依赖关系与实验结果的对比

Fig. 15. (a) The charged particle multiplicity distribution ratio, (b) the centrality dependence of average charged particle ratio, and (c) the centrality dependence of $ v_2 $ ratio in isotopic collisions for different charge separation strengths at the RHIC energy, in comparison with the STAR data

下载: 全尺寸图片幻灯片

图 16 RHIC能量的同质异位素碰撞中$ \Delta\gamma $及其比值与中心度的依赖关系

Fig. 16. Centrality dependence of $ \Delta\gamma $ and its ratio in isobar collisions at the RHIC energy

下载: 全尺寸图片幻灯片

图 17 RHIC能量的同质异位素碰撞中, 0—5%中心度中(a)$v_2\{2\}$及(b)其比值和20%—50%中心度中(c) $ v_{2}\{2\} $及(d)其比值与碰撞能量$ \sqrt{s} $的依赖关系

Fig. 17. Collision energy $ \sqrt{s} $ dependence of (a) $ v_{2}\{2\} $ and (b) its ratio in 0–5% centrality bin, and collision energy $ \sqrt {s} $ dependence of (c) $v_2\{2\}$ and (d) its ratio in 20%–50% centrality bin (lower panel) in isobar collisions at the RHIC energy

下载: 全尺寸图片幻灯片

图 18 手征磁波(CMW)示意图, 图片来自文献[35]

Fig. 18. Schematic diagram of chiral magnetic wave (CMW), which is taken from Ref. [35]

下载: 全尺寸图片幻灯片

图 19 RHIC能量30%—40%中心度$ \rm Au+Au $碰撞中, (a)初态部分子态的3%初始四极矩强度在横平面的净电荷密度分布; (b)不同初态部分子四极矩强度下斜率参数对中心度的依赖性

Fig. 19. (a) Net charge density distribution in the transverse plane for the 3% initial quadrupole charge separation for 30%–40% centrality bin in $ \rm Au + Au $ collisions at the RHIC energy; (b) centrality dependence of the slope parameter for different strengths of initial quadrupole charge separation

下载: 全尺寸图片幻灯片

图 20 (a) RHIC能量碰撞参数$ b = 10 $ fm下$ \rm Au+Au $碰撞中$e^2\langle {\boldsymbol{E}} \cdot {\boldsymbol{B}}\rangle$在横平面上的分布; (b)不同计算方法得出的$ \langle {\boldsymbol{E}}\cdot{\boldsymbol{ B}}\rangle $在$ t = 0 $时在$ y < 0 $ fm的横向平面内的分区平均密度和斜率参数的碰撞中心度依赖性

Fig. 20. (a) Spatial distributions of $ e^2\langle {\boldsymbol{E}} \cdot {\boldsymbol{B}}\rangle $ in the transverse plane at $ t = 0 $ for $ b = 10 $ fm in $ \rm Au+Au $ collisions at the RHIC energy, where the unit is $ m_\pi^4 $; (b) zone-averaged density of $ \langle {\boldsymbol{E}} \cdot {\boldsymbol{B}}\rangle $ from different calculation methods (open symbols) at $ t = 0 $ in the transverse plane of $ y < 0 $ fm and the slope parameter (red filled symbol) as functions of $ N_{{\rm{part}}} $ in $ \rm Au+Au $ collisions at the RHIC energy

下载: 全尺寸图片幻灯片

图 21 (a)$ A_{\rm ch}-\Delta v_2 $的斜率与$ \left < v_2 \right > $的依赖关系; (b)积分的三粒子关联的差与$ \left < v_2 \right > $的依赖关系

Fig. 21. (a)$ \left < v_2 \right > $ dependence of the slope of $ A_{\rm ch}-\Delta v_2 $; (b)$ \left < v_2 \right > $ dependence of the difference of the integrated three-particle correlator

下载: 全尺寸图片幻灯片

图 22 关联$ W_{2(3)} $与$ \Delta v_2 $的依赖关系, (a)四极矩为零的情况; (b)10%的四极矩; (c)不同类型的5%的四极矩

Fig. 22. $ \Delta v_2 $ dependence of the correlation $ W_{2(3)} $, (a) the case of zero quadrupole; (b) the case of quadrupole of 10%; (c) different types of cases of quadrupole of 5%

下载: 全尺寸图片幻灯片

图 23 40 MeV的$ \rm N+Pb $碰撞中光子的定向流$ v_1 $和椭圆流$ v_2 $与光子的横动量$ p_{\rm T} $的关系

Fig. 23. Direct flow $ v_1 $ and elliptical flow $ v_2 $ as functions of $ p_{\rm T} $ of photons for $ \rm N+Pb $ collisions at 40 MeV

下载: 全尺寸图片幻灯片

图 24 $\rm {}^{16}O+{}^{40}Ca$碰撞在无磁场和有磁场的情况下, GDR光谱的(a)峰值能量, (b)峰值强度和(c)光谱宽度与入射能量的关系

Fig. 24. (a) Peak energy, (b) peak intensity, and (c) spectral width of the GDR spectrum as functions of incident energy for $\rm {}^{16}O+ {}^{40}Ca$ collisions in the absence and presence of the magnetic field

下载: 全尺寸图片幻灯片

图 25 $ \rm ^{16}O+^{40}Ca $碰撞在无磁场和有磁场的情况下, (a)温度和(b)角动量$ J_y $与入射能量的关系

Fig. 25. (a) Temperature and (b) angular momentum $ J_y $ as functions of the incident energy for $ \rm ^{16}O+^{40}Ca $ collisions in the absence and presence of the magnetic field

下载: 全尺寸图片幻灯片

map

[1]	Gross D J, Wilczek F 1973 Phys. Rev. Lett. 30 1343 Google Scholar
[2]	Politzer H D 1973 Phys. Rev. Lett. 30 1346 Google Scholar
[3]	Adams J,Aggarwal M M, Ahammed Z, et al. (STAR Collaboration). 2005 Nucl. Phys. A 757 102 Google Scholar
[4]	Adcox K, Adler S S, Afanasiev S, et al. (PHENIX Collaboration). 2005 Nucl. Phys. A 757 184 Google Scholar
[5]	Aamodt K, Quintana A A, Achenbach R, et al. (ALICE Collaboration). 2008 JINST 3 S08002 Google Scholar
[6]	Bzdak A, Esumi S, Koch V, Liao J, Stephanov M, Xu N 2020 Phys. Rep. 853 1 Google Scholar
[7]	Luo X, Xu N 2017 Nucl. Sci. Tech. 28 112 Google Scholar
[8]	Xu J, Liao J, Gyulassy M 2015 Chin. Phys. Lett. 32 092501 Google Scholar
[9]	Siemens P J, Rasmussen J O 1979 Phys. Rev. Lett. 42 880 Google Scholar
[10]	Kolb P F, Sollfrank J, Heinz U W 2000 Phys. Rev. C 62 054909 Google Scholar
[11]	Teaney D, Lauret J, Shuryak E V 2001 Phys. Rev. Lett. 86 4783 Google Scholar
[12]	Song H, Heinz U W 2008 Phys. Rev. C 77 064901 Google Scholar
[13]	Jeon S, Heinz U 2015 Int. J. Mod. Phys. E 24 1530010 Google Scholar
[14]	Shen C, Yan L 2020 Nucl. Sci. Tech. 31 122 Google Scholar
[15]	Lao H L, Liu F H, Li B C, Duan M Y, Lacey R A 2018 Nucl. Sci. Tech. 29 164 Google Scholar
[16]	Waqas M, Liu F H, Li L L, Alfanda H M 2020 Nucl. Sci. Tech. 31 109 Google Scholar
[17]	Poskanzer A M, Voloshin S A 1998 Phys. Rev. C 58 1671 Google Scholar
[18]	Gale C, Jeon S, Schenke B 2013 Int. J. Mod. Phys. A 28 1340011 Google Scholar
[19]	Alver B, Roland G 2010 Phys. Rev. C 81 054905 Google Scholar
[20]	Ma G L, Wang X N 2011 Phys. Rev. Lett. 106 162301 Google Scholar
[21]	Ma L, Ma G L, Ma Y G 2016 Phys. Rev. C 94 044915 Google Scholar
[22]	Lee T D, Yang C N 1956 Phys. Rev. 104 254 Google Scholar
[23]	Christenson J H, Cronin J W, Fitch V L, Turlay R 1964 Phys. Rev. Lett. 13 138 Google Scholar
[24]	Skokov V, Illarionov A Y, Toneev V 2009 Int. J. Mod. Phys. A 24 5925 Google Scholar
[25]	Bzdak A, Skokov V 2012 Phys. Lett. B 710 171 Google Scholar
[26]	Deng W T, Huang X G 2012 Phys. Rev. C 85 044907 Google Scholar
[27]	Hattori K, Huang X G 2017 Nucl. Sci. Tech. 28 26 Google Scholar
[28]	Rojas H P, Martinez A P, Cuesta H J M 2004 Chin. Phys. Lett. 21 2117 Google Scholar
[29]	Kharzeev D 2006 Phys. Lett. B 633 260 Google Scholar
[30]	Kharzeev D, Zhitnitsky A 2007 Nucl. Phys. A 797 67 Google Scholar
[31]	Kharzeev D E, McLerran L D, Warringa H J 2008 Nucl. Phys. A 803 227 Google Scholar
[32]	Fukushima F, Kharzeev D E, Warringa H J 2008 Phys. Rev. D 78 074033 Google Scholar
[33]	Son D T, Zhitnitsky A R 2004 Phys. Rev. D 70 074018 Google Scholar
[34]	Metlitski M A, Zhitnitsky A R 2005 Phys. Rev. D 72 045011 Google Scholar
[35]	Kharzeev D E, Liao J F, Voloshin S A, Wang G 2016 Prog. Part. Nucl. Phys. 88 1 Google Scholar
[36]	Kharzeev D E, Yee H U 2011 Phys. Rev. D 83 085007 Google Scholar
[37]	罗晓丽, 高建华 2023 72 112503 Google Scholar Luo X L, Gao J H 2023 Acta Phys. Sin. 72 112503 Google Scholar
[38]	Bertsch G F, Gupta S D 1988 Phys. Rep. 160 189 Google Scholar
[39]	Maruyama T, Niita K, Iwamoto A 1996 Phys. Rev. C 53 297 Google Scholar
[40]	Lin Z W, Ko C M, Li B A, Zhang B, Pal S 2005 Phys. Rev. C 72 064901 Google Scholar
[41]	Zhao X L, Ma Y G, Ma G L 2018 Phys. Rev. C 97 024910 Google Scholar
[42]	Zhao X L, Ma G L, Ma Y G 2019 Phys. Rev. C 99 034903 Google Scholar
[43]	Deng W T, Huang X G, Ma G L, Wang G 2018 Phys. Rev. C 97 044901 Google Scholar
[44]	Cheng Y L, Zhang S, Ma Y G, Chen J H, Zhong C 2019 Phys. Rev. C 99 054906 Google Scholar
[45]	Chen Y, Sheng X L, Ma G L 2021 Nucl. Phys. A 1011 122199 Google Scholar
[46]	Zhong Y, Yang C B, Cai X, Feng S Q 2015 Chin. Phys. C 39 104105 Google Scholar
[47]	Kharzeev D E, Liao J F 2021 Nat. Rev. Phys. 3 55 Google Scholar
[48]	Huang X G 2016 Rept. Prog. Phys. 79 076302 Google Scholar
[49]	Gao J H, Ma G L, Pu S, Wang Q 2020 Nucl. Sci. Tech. 31 90 Google Scholar
[50]	Voloshin S A 2004 Phys. Rev. C 70 057901 Google Scholar
[51]	Abelev B I, Aggarwal M M, Ahammed Z, et al. [STAR]. 2009 Phys. Rev. Lett. 103 251601 Google Scholar
[52]	Abelev B I, Aggarwal M M, Ahammed Z, et al. 2010 Phys. Rev. C 81 054908 Google Scholar
[53]	Adamczyk L, Adkins J K, Agakishiev G, et al. [STAR]. 2013 Phys. Rev. C 88 064911 Google Scholar
[54]	Adamczyk L, Adkins J K, Agakishiev G, et al. [STAR]. 2014 Phys. Rev. Lett. 113 052302 Google Scholar
[55]	Abelev B, Adam J, Adamova D, et al. [ALICE]. 2013 Phys. Rev. Lett. 110 012301 Google Scholar
[56]	Lin Z W, Zheng L 2021 Nucl. Sci. Tech. 32 113 Google Scholar
[57]	Ma G L, Zhang B 2011 Phys. Lett. B 700 39 Google Scholar
[58]	Shou Q Y, Ma G L, Ma Y G 2014 Phys. Rev. C 90 047901 Google Scholar
[59]	Huang L, Ma C W, Ma G L 2018 Phys. Rev. C 97 034909 Google Scholar
[60]	Huang L, Nie M W, Ma G L 2020 Phys. Rev. C 101 024916 Google Scholar
[61]	Khachatryan V, Sirunyan A M, Tumasyan A, et al. [CMS]. 2017 Phys. Rev. Lett. 118 122301 Google Scholar
[62]	Zhang Z W, Cen X Z, Deng W T 2022 Chin. Phys. C 46 084103 Google Scholar
[63]	Bzdak A, Koch V, Liao J 2011 Phys. Rev. C 83 014905 Google Scholar
[64]	Liao J, Koch V, Bzdak A 2010 Phys. Rev. C 82 054902 Google Scholar
[65]	Schlichting S, Pratt S 2011 Phys. Rev. C 83 014913 Google Scholar
[66]	Wang F 2010 Phys. Rev. C 81 064902 Google Scholar
[67]	Zhao J [STAR] 2021 Nucl. Phys. A 1005 121766 Google Scholar
[68]	Zhao J, Wang F 2019 Prog. Part. Nucl. Phys. 107 200 Google Scholar
[69]	Wang F 2022 Acta Phys. Polon. Supp. 16 15
[70]	Li W, Wang G 2020 Ann. Rev. Nucl. Part. Sci. 70 293 Google Scholar
[71]	Voloshin S A 2010 Phys. Rev. Lett. 105 172301 Google Scholar
[72]	Deng W T, Huang X G, Ma G L, Wang G 2016 Phys. Rev. C 94 041901 Google Scholar
[73]	Adam J, Adamczyk L, Adams J R, et al. [STAR]. 2021 Nucl. Sci. Tech. 32 48 Google Scholar
[74]	Abdallah M, Aboona B E, Adam J, et al. [STAR]. 2022 Phys. Rev. C 105 014901 Google Scholar
[75]	Xu H J, Li H, Wang X, Shen C, Wang F 2021 Phys. Lett. B 819 136453 Google Scholar
[76]	Xu H J, Zhao W, Li H, Zhou Y, Chen L W, Wang F 2021 arXiv: 2111.14812 [nucl-th]
[77]	Zhang C, Jia J 2022 Phys. Rev. Lett. 128 022301 Google Scholar
[78]	Jia J, Zhang C J 2023 Phys. Rev. C 107 L021901 Google Scholar
[79]	Jia J 2022 Phys. Rev. C 105 014905 Google Scholar
[80]	Jia J 2022 Phys. Rev. C 105 044905 Google Scholar
[81]	Zhao X L, Ma G L 2022 Phys. Rev. C 106 034909 Google Scholar
[82]	Kharzeev D E, Liao J, Shi S 2022 Phys. Rev. C 106 L051903Google Scholar
[83]	Li F, Ma Y G, Zhang S, Ma G L, Shou Q, Shou Q Y 2022 Phys. Rev. C 106 014906 Google Scholar
[84]	Wang F Q, Zhao J 2018 Nucl. Sci. Tech. 29 179 Google Scholar
[85]	Xu H J, Zhao J, Wang X, Li H, Lin Z W, Shen C, Wang F 2018 Chin. Phys. C 42 084103 Google Scholar
[86]	Choudhury S, Dong X, Drachenberg J, et al. 2022 Chin. Phys. C 46 014101 Google Scholar
[87]	Tang A H 2020 Chin. Phys. C 44 054101 Google Scholar
[88]	Liang G R, Liao H F, Lin S, Yan Li, Li M 2020 Chin. Phys. C 44 094103 Google Scholar
[89]	Chen B X, Feng S Q 2020 Chin. Phys. C 44 024104 Google Scholar
[90]	Feng S Q, Pei L, Sun F, Zhong Y, Yin Z B 2018 Chin. Phys. C 42 054102 Google Scholar
[91]	Jiang Y, Shi S, Yin Y, Liao J 2018 Chin. Phys. C 42 011001 Google Scholar
[92]	Yee H U, Yin Y 2014 Phys. Rev. C 89 044909 Google Scholar
[93]	Taghavi S F, Wiedemann U A 2015 Phys. Rev. C 91 024902 Google Scholar
[94]	Hongo M, Hirono Y, Hirano T 2017 Phys. Lett. B 775 266 Google Scholar
[95]	Adamczyk L, Adkins J K, Agakishiev G, et al. [STAR]. 2015 Phys. Rev. Lett. 114 252302 Google Scholar
[96]	Adam J, Adamova D, Aggarwal M M, et al. [ALICE]. 2016 Phys. Rev. C 93 044903 Google Scholar
[97]	Ma G L 2014 Phys. Lett. B 735 383 Google Scholar
[98]	Zhao X L, Ma G L, Ma Y G 2019 Phys. Lett. B 792 413 Google Scholar
[99]	Wang C Z, Wu W Y, Shou Q Y, Ma G L, Ma Y G, Zhang S 2021 Phys. Lett. B 820 136580 Google Scholar
[100]	Wu W Y, Shou Q Y, Christakoglou P, Das P, Haque M R, Ma G L, Ma Y G, Mohanty B, Wang C Z, Zhang S, Zhao J 2023 Phys. Rev. C 107 L031902 Google Scholar
[101]	Shen D Y, Chen J H, Ma G L, Ma Y G, Shou Q Y, Zhang S, Zhong C 2019 Phys. Rev. C 100 064907 Google Scholar
[102]	Deng X G, Ma Y G 2018 Eur. Phys. J. A 54 204 Google Scholar
[103]	Cao Y T, Deng X G, Ma Y G 2022 Phys. Rev. C 106 014611 Google Scholar
[104]	阮丽娟, 许长补, 杨驰 2023 72 112401 Google Scholar Ruan L J, Xu Z B, Yang C 2023 Acta Phys. Sin. 72 112401 Google Scholar
[105]	寿齐烨, 赵杰, 徐浩洁, 李威, 王钢, 唐爱洪, 王福强 2023 72 112504 Google Scholar Shou Q Y, Zhao J, Xu H J, Li W, Wang G, Tang A H, Wang F Q 2023 Acta Phys. Sin. 72 112504 Google Scholar
[106]	高建华, 盛欣力, 王群, 庄鹏飞 2023 72 112501 Google Scholar Gao J H, Sheng X L, Wang Q, Zhuang P F 2023 Acta Phys. Sin. 72 112501 Google Scholar
[107]	浦实, 黄旭光 2023 72 071202 Google Scholar Pu S, Huang X G 2023 Acta Phys. Sin. 72 071202 Google Scholar

[1]	霍冠忠, 苏超, 王可, 叶晴莹, 庄彬, 陈水源, 黄志高. 铁酸铋薄膜光电流的磁场调制研究. , 2023, 72(6): 067501. doi: 10.7498/aps.72.20222053
[2]	寿齐烨, 赵杰, 徐浩洁, 李威, 王钢, 唐爱洪, 王福强. 相对论重离子碰撞中的手征效应实验研究. , 2023, 72(11): 112504. doi: 10.7498/aps.72.20230109
[3]	崔翔. 电流连续的细导体段模型的磁场及电感. , 2020, 69(3): 034101. doi: 10.7498/aps.69.20191212
[4]	孟令辉, 任洪波, 刘建晓. 高温等离子体中太赫兹波的传输特性. , 2018, 67(17): 174101. doi: 10.7498/aps.67.20180647
[5]	于振涛, 吕俊伟, 毕波, 周静. 四面体磁梯度张量系统的载体磁干扰补偿方法. , 2014, 63(11): 110702. doi: 10.7498/aps.63.110702
[6]	成玉国, 程谋森, 王墨戈, 李小康. 磁场对螺旋波等离子体波和能量吸收影响的数值研究. , 2014, 63(3): 035203. doi: 10.7498/aps.63.035203
[7]	张红, 张春元, 张慧亮, 刘建军. 外加磁场下抛物型量子线中的带电激子. , 2011, 60(7): 077301. doi: 10.7498/aps.60.077301
[8]	姜文龙, 孟昭晖, 丛林, 汪津, 王立忠, 韩强, 孟凡超, 高永慧. 双量子阱结构OLED效率和电流的磁效应. , 2010, 59(9): 6642-6646. doi: 10.7498/aps.59.6642
[9]	邹秀, 邹滨雁, 刘惠平. 外加磁场对碰撞射频鞘层离子能量分布的影响. , 2009, 58(9): 6392-6396. doi: 10.7498/aps.58.6392
[10]	陈杰, 鲁习文. 基于磁荷面分布的舰船磁场预测方法. , 2009, 58(6): 3839-3843. doi: 10.7498/aps.58.3839
[11]	汪津, 华杰, 丁桂英, 常喜, 张刚, 姜文龙. 磁场作用下的有机电致发光. , 2009, 58(10): 7272-7277. doi: 10.7498/aps.58.7272
[12]	张雯. 磁场微重力效应的研究. , 2009, 58(4): 2405-2409. doi: 10.7498/aps.58.2405
[13]	罗成林, 杨兵初, 戎茂华. 磁场对滤纸上Zn电解沉积物形貌的影响. , 2006, 55(7): 3778-3784. doi: 10.7498/aps.55.3778
[14]	张助华, 郭万林, 郭宇锋. 轴向磁场对碳纳米管电子性质的影响. , 2006, 55(12): 6526-6531. doi: 10.7498/aps.55.6526
[15]	韩逸, 班春燕, 巴启先, 王书晗, 崔建忠. 磁场对液态铝和固态铁界面微观组织的影响. , 2005, 54(6): 2955-2960. doi: 10.7498/aps.54.2955
[16]	李玉现, 刘建军, 李伯臧. 量子点接触中的电导与热功率：磁场与温度的影响. , 2005, 54(3): 1366-1369. doi: 10.7498/aps.54.1366
[17]	黄维清, 陈克求, 帅志刚, 王玲玲, 胡望宇. 磁耦合效应对半无限超晶格中表面电子态的影响. , 2004, 53(7): 2330-2335. doi: 10.7498/aps.53.2330
[18]	欧阳世根, 关毅, 佘卫龙. 旋转超导体中的电流与电磁场. , 2002, 51(7): 1596-1599. doi: 10.7498/aps.51.1596
[19]	陈正林, 张杰. 对超热电子诱生的磁场分布的估算. , 2001, 50(4): 735-740. doi: 10.7498/aps.50.735
[20]	陈正林, 张杰. 对超热电子诱生的磁场分布的估算. , 2000, 49(11): 2180-2185. doi: 10.7498/aps.49.2180

计量

文章访问数: 4748
PDF下载量: 120
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

中高能重离子碰撞中的电磁场效应和手征反常现象