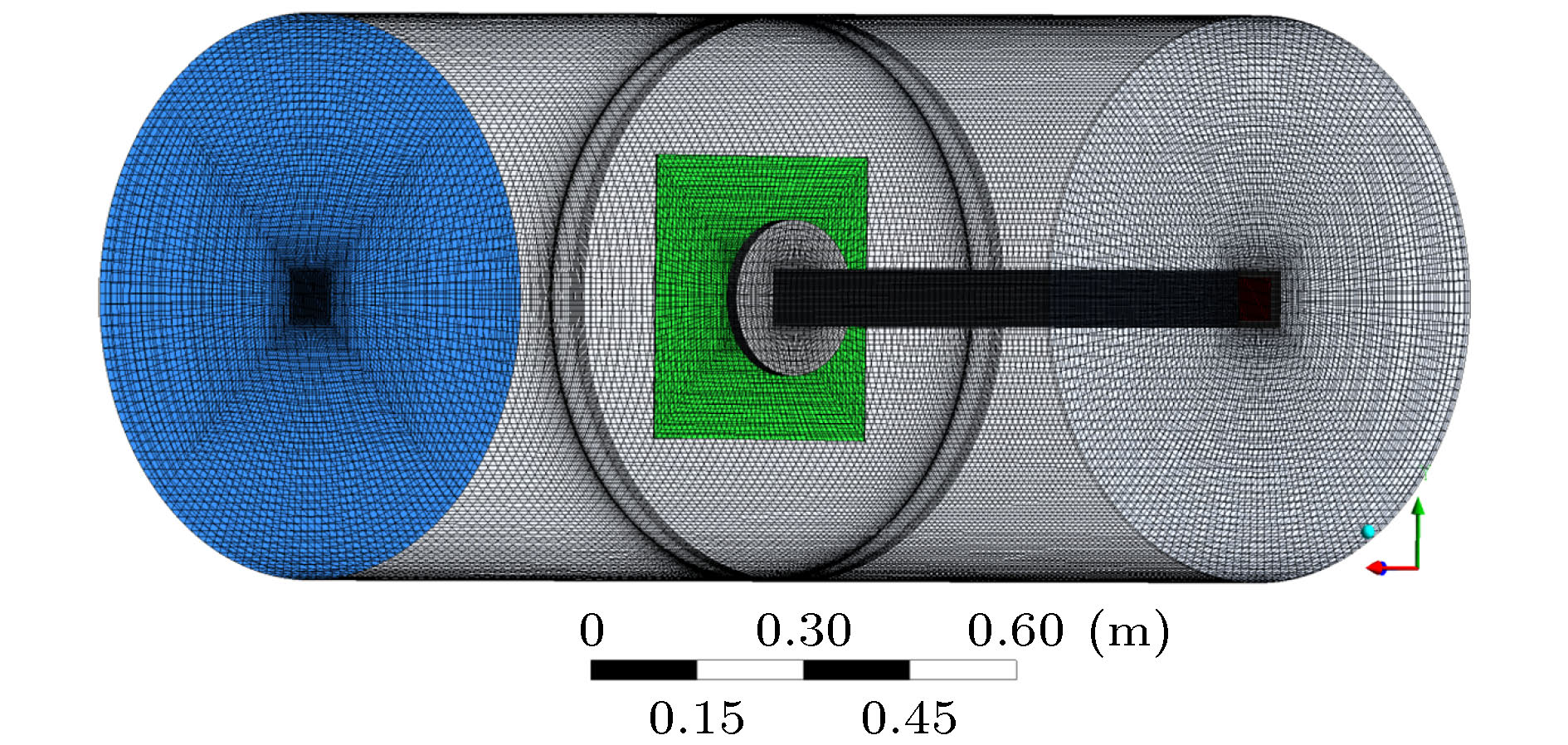
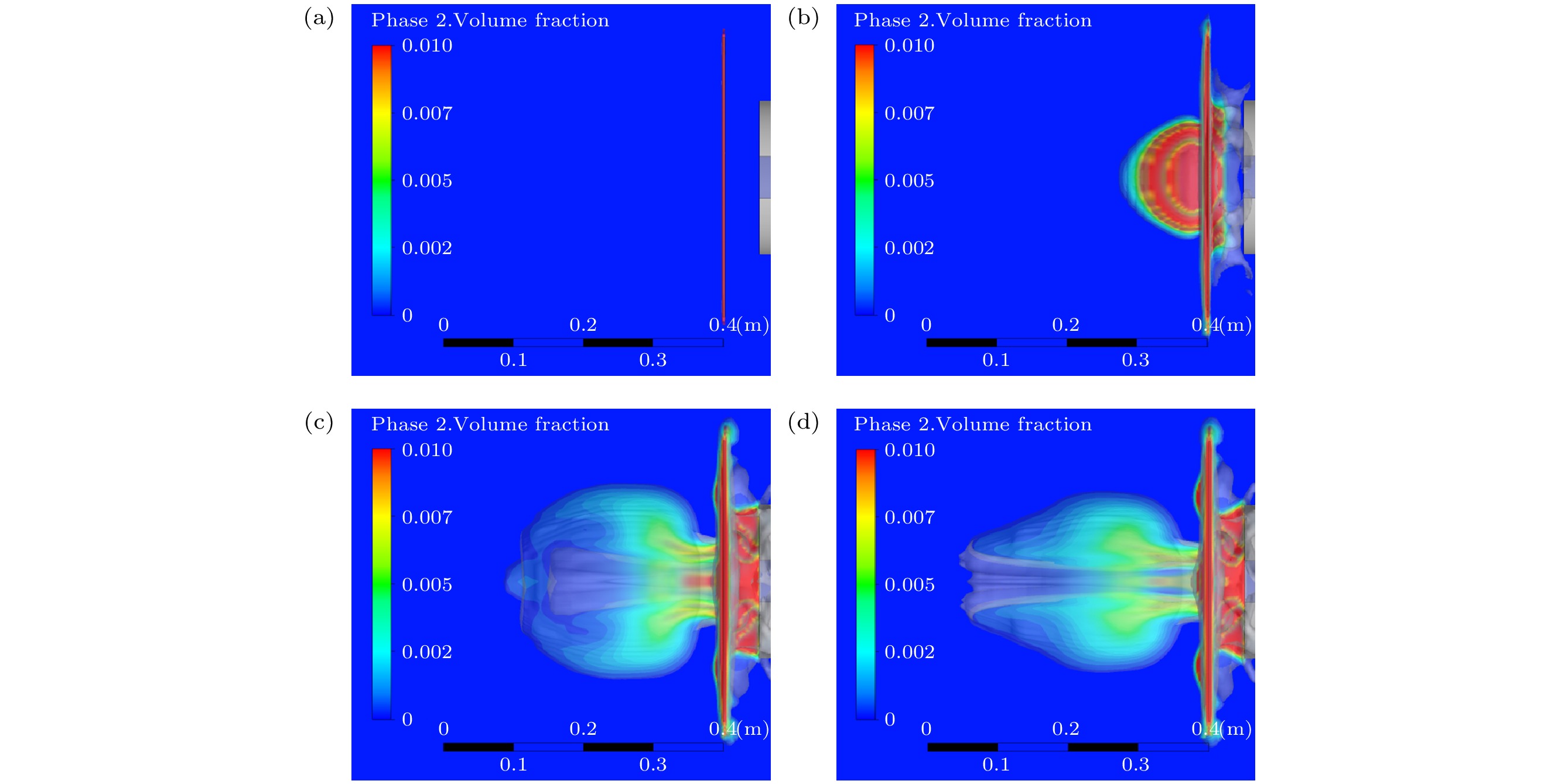
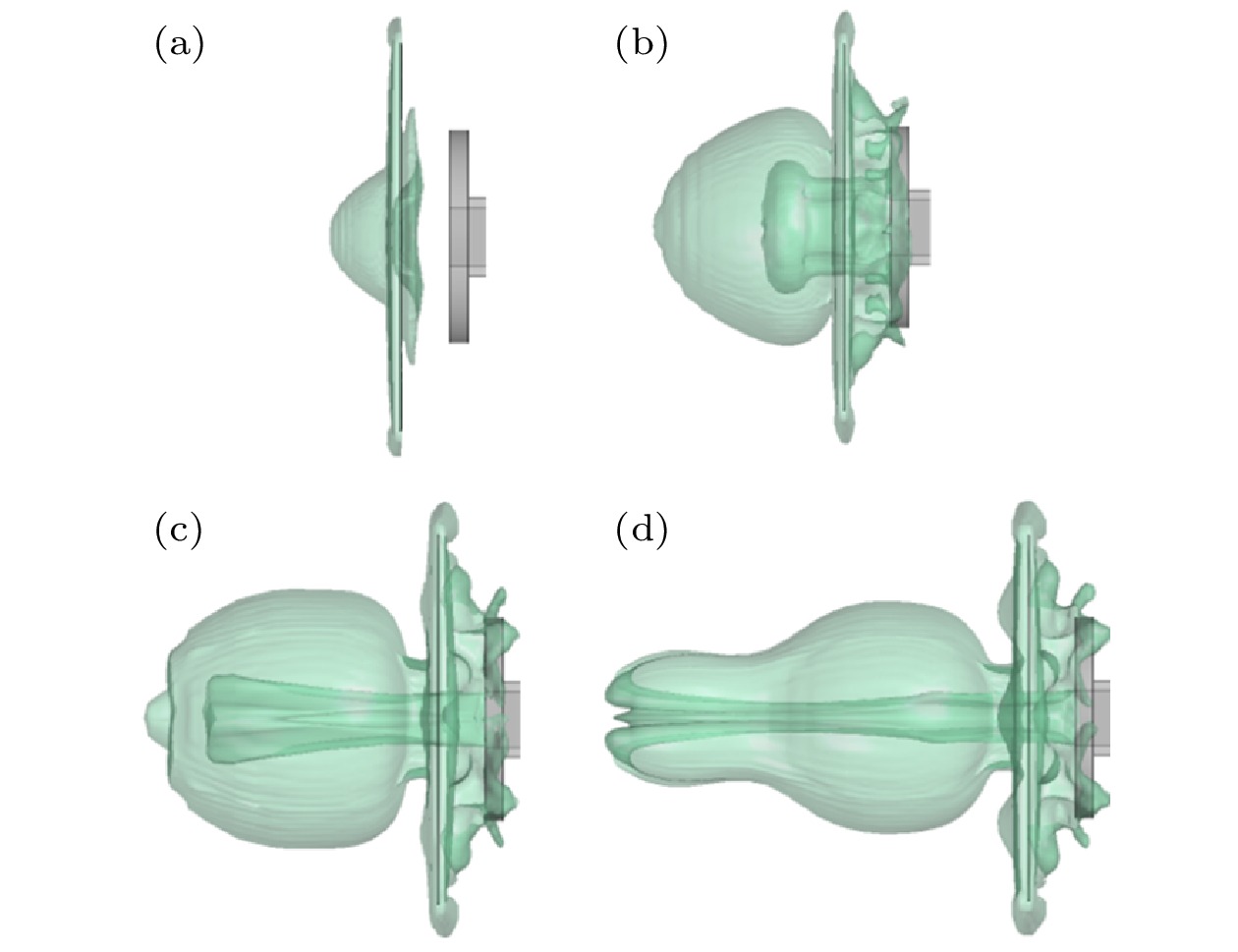
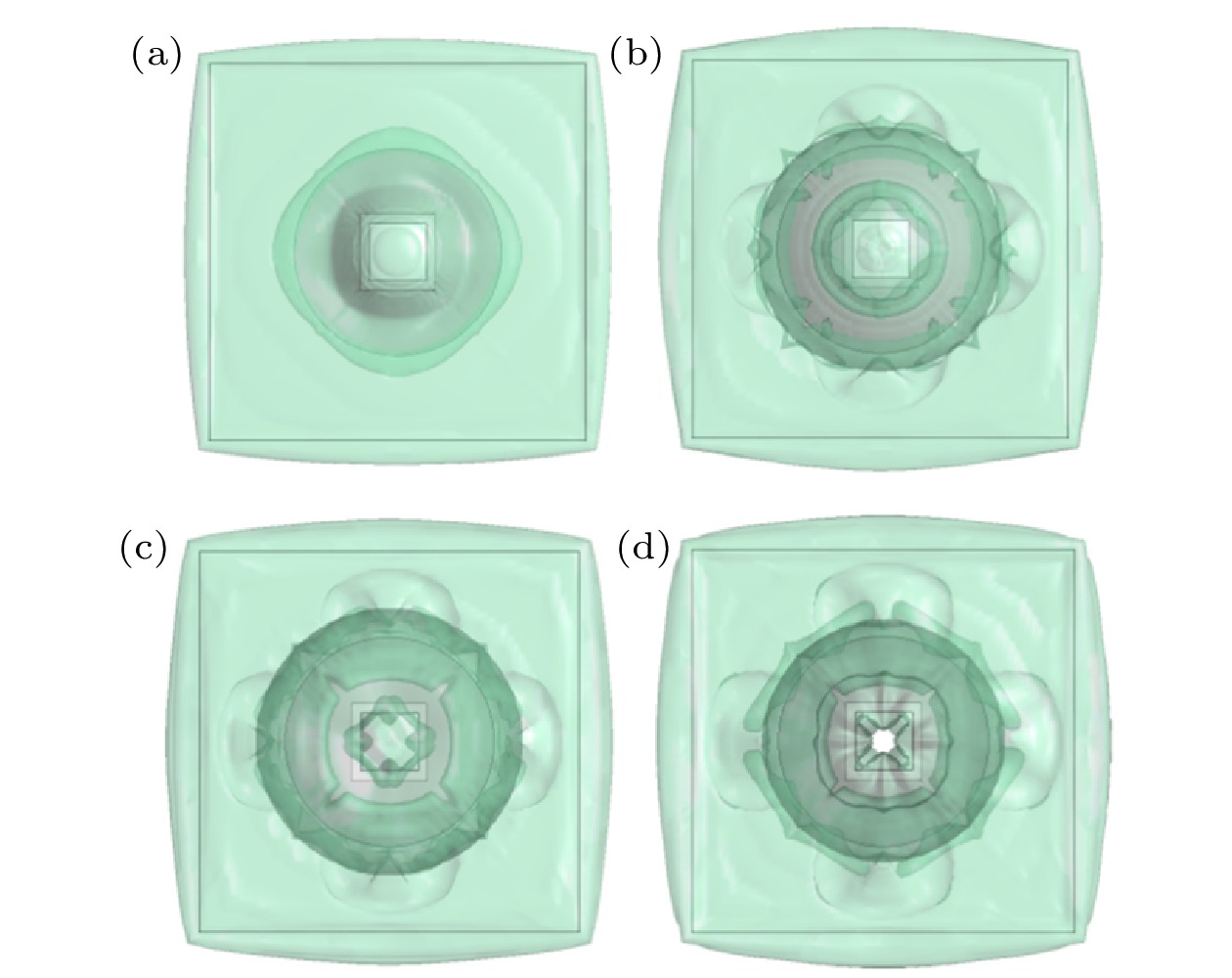
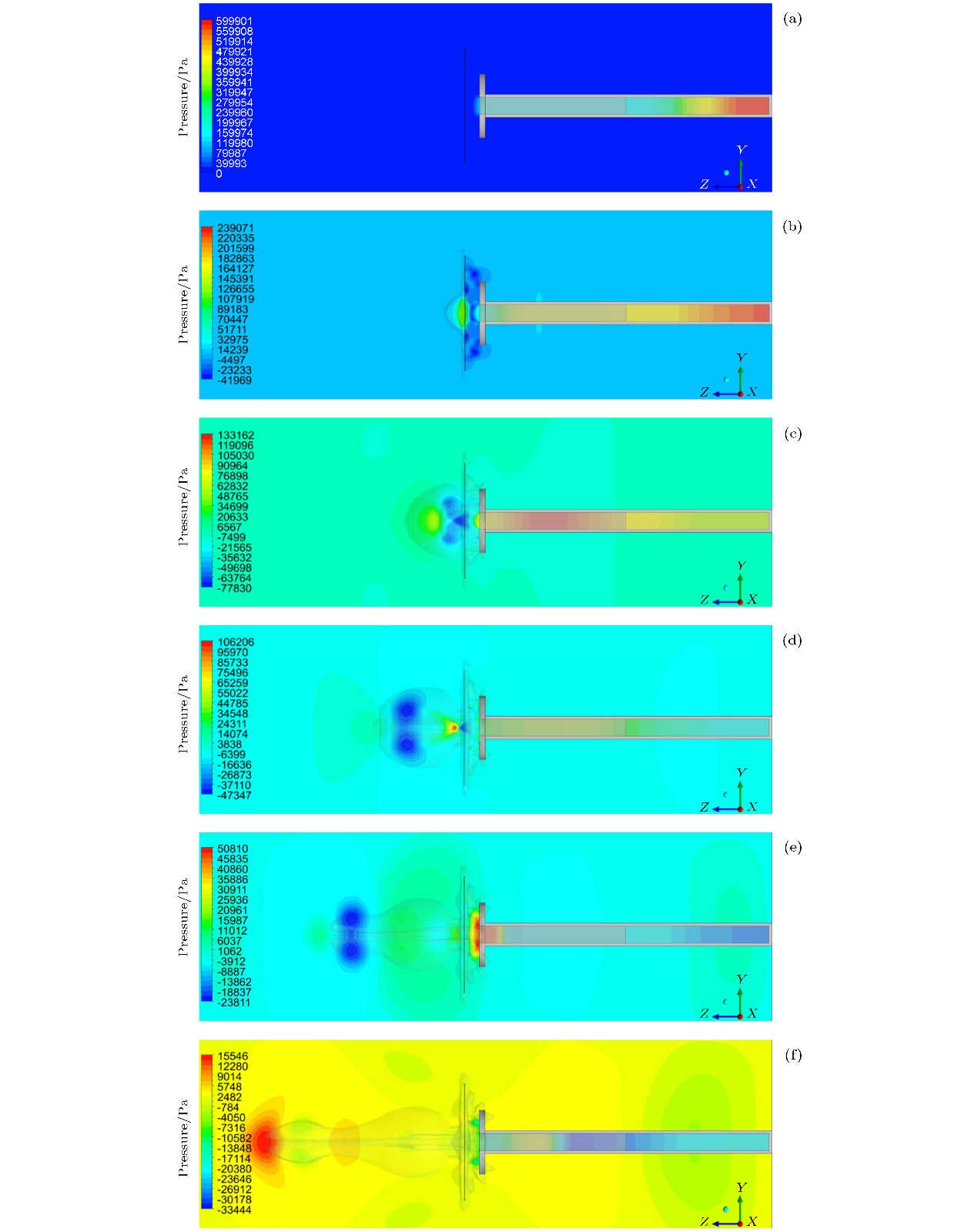
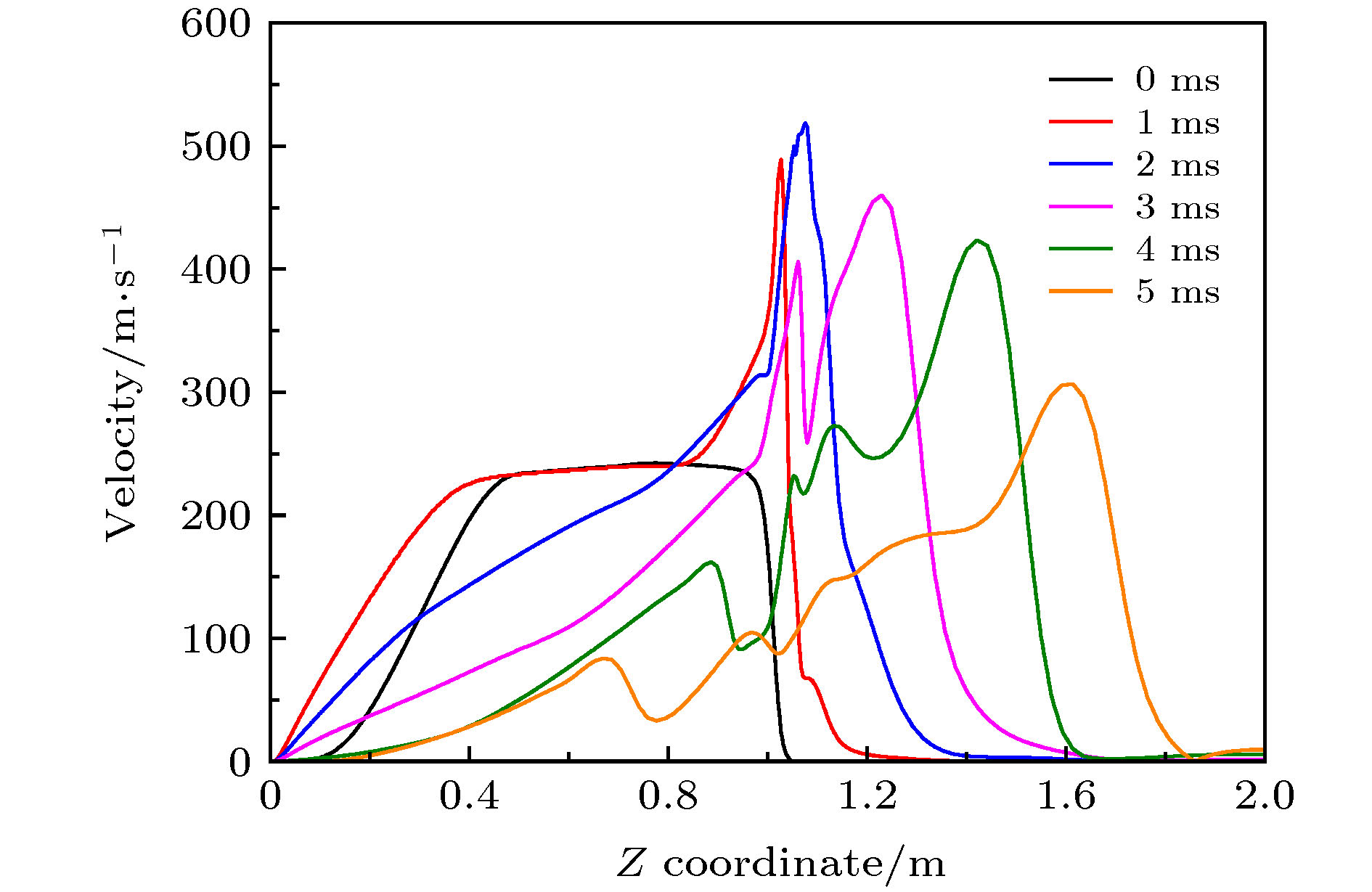
-
The gas-liquid two-phase flow of liquid dispersing and breaking under the action of shock wave includes complex physical phenomena, such as turbulent mixing of gas-liquid two-phase, instability and breakage of liquid interface, and formation of internal cavity structure after atomization. In order to investigate the shock-wave-caused breaking process of the liquid film, a three-dimensional numerical simulation of the gas-liquid two-phase flow process is performed by using the computational fluid dynamics method. In the simulation, the Mach number of shock wave is 1.5 and the thickness of liquid film is 2 mm. The finite volume method is used to solve the three-dimensional Navier-Stokes equation. The volume of fluid model is applied to the gas-liquid two-phase flow. The k-ε double equation turbulence model is selected for the turbulence calculation. The evolution process of the wave system structure of the shock wave and the deformation, breakage and atomization characteristics of the liquid film are obtained, and compared with the experimental results. The results show that the incidence, reflection, and transmission phenomena occur during the interaction between the shock wave and the liquid film, and the intensity of the transmitted shock wave and the liquid surface tension have an important effect on the breaking process of the liquid film. The transmitted shock wave affects the shape of the broken cloud cluster on the left of the liquid film, while the incident shock wave and reflected shock wave affect the shape of the broken cloud cluster on the right side of the liquid film. The volume of the atomized cloud formed in the breaking process of the liquid film increases rapidly, first reaching 6.7 dm3 within 2.5 ms, then keeping stable basically. After the shock wave exits from the tube, a long narrow jet is formed. The maximum velocity reaches 519 m/s and appears in the interior of the jet, and then decreases continuously. Under the action of the jet, an expanding three-dimensional cavity structure is formed inside the atomizing cloud, and an annular vortex with negative pressure in the core area occurs in the cavity structure. Finally, the annular vortex continuously entrains the surrounding fluid in the process of forward movement, the strength of the vortex decreases and gradually dissipates in the space. This work is conducive to further understanding the interaction process of gas-liquid two-phase flow.
-
Keywords:
- breaking process of liquid film /
- gas-liquid two-phase flow /
- computational fluid dynamics /
- shock wave
[1] 戴剑锋, 樊学萍, 蒙波, 刘骥飞 2015 64 094704
Google Scholar
Dai J F, Fan X P, Meng B, Liu J F 2015 Acta Phys. Sin. 64 094704
Google Scholar
[2] Zhang Y, Cao W G, Shu C M, Zhao M K, Yu C J, Xie Z B, Liang J H, Song Z Q, Cao X 2020 Fuel 261 116433
Google Scholar
[3] Batchelor G K, Wen C S 1982 J. Fluid Mech. 124 495
Google Scholar
[4] Whitby E R, McMurry P H 1997 Aerosol Sci. Technol. 27 673
Google Scholar
[5] Pilch M, Erdman C A 1987 Int. J. Multiphase Flow 13 741
Google Scholar
[6] Hsiang L P, Faeth G M 1995 Int. J. Multiphase Flow 21 545
Google Scholar
[7] Hsiang L P, Faeth G M 1992 Int. J. Multiphase Flow 18 635
Google Scholar
[8] Hsiang L P, Faeth G M 1993 Int. J. Multiphase Flow 19 721
Google Scholar
[9] Orme M 1997 Progress in Energy and Combustion Science 23 65
Google Scholar
[10] 黄勇, 解立峰, 叶经方, 鲁长波, 安高军, 熊春华, 李永坚, 徐淳 2016 高压 30 227
Google Scholar
Huang Y, Xie L F, Ye J F, Lu C B, An G J, Xiong C H, Li Y J, Xu C 2016 Chin. J. High Press. Phys. 30 227
Google Scholar
[11] 黄熙龙, 刘金宏, 廖深飞, 吴鋆 2018 中国科学: 物理学 力学 天文学 48 054701
Huang X L, Liu J H, Liao S F, Wu Y 2018 Sci. China, Ser. G 48 054701
[12] 陆守香, 秦友花 2000 高压 14 151
Google Scholar
Lu S X, Qin Y H 2000 Chin. J. High Pressure Phys. 14 151
Google Scholar
[13] 沙莎, 陈志华, 张庆兵 2015 64 015201
Google Scholar
Sha S, Chen Z H, Zhang Q B 2015 Acta Phys. Sin. 64 015201
Google Scholar
[14] 沙莎, 陈志华, 薛大文 2013 62 144701
Google Scholar
Sha S, Chen Z H, Xue D W 2013 Acta Phys. Sin. 62 144701
Google Scholar
[15] Si T, Zhai Z G, Yang J M, Luo X S 2012 Phys. Fluids 24 054101
Google Scholar
[16] 丁珏, 刘家骢 2001 兵工学报 22 481
Google Scholar
Ding Y, Liu J C 2001 Acta Arimam. 22 481
Google Scholar
[17] 梁煜, 关奔, 翟志刚, 罗喜胜 2017 66 064701
Google Scholar
Liang Y, Guan B, Zhai Z G, Luo X S 2017 Acta Phys. Sin. 66 064701
Google Scholar
[18] Faeth G M, Hsiang L P, Wu P K 1995 Int. J. Multiphase Flow 21 99
Google Scholar
[19] Chou W H, Hsiang L P, Faeth G M 1997 Int. J. Multiphase Flow 23 651
Google Scholar
[20] Batchelor G K1967 An Introduction to Fluid Dynamics (Oxford: Cambridge University Press)pp137−171
[21] 李斌 2012 博士学位论文(南京: 南京理工大学)
Li B 2012 Ph. D. Dissertation (Nanjing: Nanjing University of Science and Technology) (in Chinese)
-
图 1 激波与液膜作用系统几何结构图
Figure 1. Geometry of the interaction system between shock wave and liquid film.
图 2 计算域网格划分
Figure 2. Mesh generation of the calculation domain.
图 3 液膜破碎形态演变实验结果[21] (a) t = 0 ms; (b) t =1.5 ms; (c) t = 3 ms; (d) t = 3.5 ms
Figure 3. Experiment results of liquid film breaking evolution: (a) t = 0 ms; (b) t = 1.5 ms; (c) t = 3 ms; (d) t = 3.5 ms.
图 4 液膜破碎形态演变仿真结果 (a) t = 0 ms; (b) t = 1.5 ms; (c) t = 3 ms; (d) t = 3.5 ms
Figure 4. Simulation results of liquid film breaking evolution: (a) t = 0 ms; (b) t = 1.5 ms; (c) t = 3 ms; (d) t = 3.5 ms.
图 5 液膜抛撒距离的仿真与实验对比
Figure 5. Comparison of simulation and experiment on the dispersal distance of liquid film.
图 6 侧向视角下液膜破碎过程 (a) t = 1 ms; (b) t = 2 ms; (c) t = 3 ms; (d) t = 4 ms
Figure 6. Process of liquid film breaking in side view: (a) t = 1 ms; (b) t = 2 ms; (c) t = 3 ms; (d) t = 4 ms.
图 7 正向视角下液膜破碎过程 (a) t = 1 ms; (b) t = 2 ms; (c) t = 3 ms; (d) t = 4 ms
Figure 7. Process of liquid film breaking in front view: (a) t = 1 ms; (b) t = 2 ms; (c) t = 3 ms; (d) t = 4 ms.
图 8 液膜破碎形成的云团体积变化过程
Figure 8. Process of cloud volume change caused by liquid film breaking.
图 9 激波与液膜作用过程压力变化 (a) t = 0 ms; (b) t = 1 ms; (c) t = 2 ms; (d) t = 3 ms; (e) t = 4 ms; (f) t = 4 ms
Figure 9. Pressure change during the interaction between shock wave and liquid film: (a) t = 0 ms; (b) t = 1 ms; (c) t = 2 ms; (d) t = 3 ms; (e) t = 4 ms; (f) t = 4 ms.
图 10 不同时刻激波管中轴线上压力分布
Figure 10. Pressure distribution on the central axis of shock tube at different times.
图 11 激波与液膜作用过程速度变化 (a) t = 0 ms; (b) t = 1 ms; (c) t = 2 ms; (d) t = 3 ms; (e) t = 4 ms; (f) t = 5 ms
Figure 11. Velocity change during the interaction between shock wave and liquid film: (a) t = 0 ms; (b) t = 1 ms; (c) t = 2 ms; (d) t = 3 ms; (e) t = 4 ms; (f) t = 5 ms.
图 12 不同时刻激波管中轴线上速度分布
Figure 12. Velocity distribution on the central axis of shock tube at different times.
-
[1] 戴剑锋, 樊学萍, 蒙波, 刘骥飞 2015 64 094704
Google Scholar
Dai J F, Fan X P, Meng B, Liu J F 2015 Acta Phys. Sin. 64 094704
Google Scholar
[2] Zhang Y, Cao W G, Shu C M, Zhao M K, Yu C J, Xie Z B, Liang J H, Song Z Q, Cao X 2020 Fuel 261 116433
Google Scholar
[3] Batchelor G K, Wen C S 1982 J. Fluid Mech. 124 495
Google Scholar
[4] Whitby E R, McMurry P H 1997 Aerosol Sci. Technol. 27 673
Google Scholar
[5] Pilch M, Erdman C A 1987 Int. J. Multiphase Flow 13 741
Google Scholar
[6] Hsiang L P, Faeth G M 1995 Int. J. Multiphase Flow 21 545
Google Scholar
[7] Hsiang L P, Faeth G M 1992 Int. J. Multiphase Flow 18 635
Google Scholar
[8] Hsiang L P, Faeth G M 1993 Int. J. Multiphase Flow 19 721
Google Scholar
[9] Orme M 1997 Progress in Energy and Combustion Science 23 65
Google Scholar
[10] 黄勇, 解立峰, 叶经方, 鲁长波, 安高军, 熊春华, 李永坚, 徐淳 2016 高压 30 227
Google Scholar
Huang Y, Xie L F, Ye J F, Lu C B, An G J, Xiong C H, Li Y J, Xu C 2016 Chin. J. High Press. Phys. 30 227
Google Scholar
[11] 黄熙龙, 刘金宏, 廖深飞, 吴鋆 2018 中国科学: 物理学 力学 天文学 48 054701
Huang X L, Liu J H, Liao S F, Wu Y 2018 Sci. China, Ser. G 48 054701
[12] 陆守香, 秦友花 2000 高压 14 151
Google Scholar
Lu S X, Qin Y H 2000 Chin. J. High Pressure Phys. 14 151
Google Scholar
[13] 沙莎, 陈志华, 张庆兵 2015 64 015201
Google Scholar
Sha S, Chen Z H, Zhang Q B 2015 Acta Phys. Sin. 64 015201
Google Scholar
[14] 沙莎, 陈志华, 薛大文 2013 62 144701
Google Scholar
Sha S, Chen Z H, Xue D W 2013 Acta Phys. Sin. 62 144701
Google Scholar
[15] Si T, Zhai Z G, Yang J M, Luo X S 2012 Phys. Fluids 24 054101
Google Scholar
[16] 丁珏, 刘家骢 2001 兵工学报 22 481
Google Scholar
Ding Y, Liu J C 2001 Acta Arimam. 22 481
Google Scholar
[17] 梁煜, 关奔, 翟志刚, 罗喜胜 2017 66 064701
Google Scholar
Liang Y, Guan B, Zhai Z G, Luo X S 2017 Acta Phys. Sin. 66 064701
Google Scholar
[18] Faeth G M, Hsiang L P, Wu P K 1995 Int. J. Multiphase Flow 21 99
Google Scholar
[19] Chou W H, Hsiang L P, Faeth G M 1997 Int. J. Multiphase Flow 23 651
Google Scholar
[20] Batchelor G K1967 An Introduction to Fluid Dynamics (Oxford: Cambridge University Press)pp137−171
[21] 李斌 2012 博士学位论文(南京: 南京理工大学)
Li B 2012 Ph. D. Dissertation (Nanjing: Nanjing University of Science and Technology) (in Chinese)
DownLoad:
Catalog
Metrics
- Abstract views: 6319
- PDF Downloads: 122
- Cited By: 0
