-
Astrophysical jets are highly collimated supersonic plasma beams distributed across various astrophysical backgrounds. The triggering mechanism, collimation transmission, and stability of jets have always been a research hotspot of astrophysics. In recent years, observations and laboratory research have found that the magnetic field plays a crucial role in jet collimation, transmission, and acceleration. In this work, the two-dimensional numerical simulation of the jet in front of the CH plane target driven by an intense laser is carried out by using the open-source MHD FLASH simulation program. We systematically investigate the dynamic behaviors of jet evolution caused by the Biermann self-generated magnetic field, the external magnetic field with different directions and initial strengths and compare them with each other. Simulation results show that the Biermann self-generated magnetic field does not affect the jet interface dynamics. The external magnetic field has a redirecting effect on the plasma outflow. The external magnetic field, which is parallel to the direction of the plasma outflow center in front of the target, is conducive to the generation and collimation of the jet. The evolution of the jet goes through three stages: antimagnetic ellipsoid cavity, conical nozzle, and collimated jet. Its formation process and evolution process result from competition among plasma thermal, magnetic, and ram pressure. In terms of force, plasma thermal pressure gradient and magnetic pressure forces play a decisive role in the jet evolution process. The presence of magnetic pressure significantly limits the radial expansion of the jet to achieve axial collimation transmission. The length-diameter ratio of the jet is positively correlated with the initial axial applied magnetic field intensity. In addition, we observe in the simulation that there are many node-like structures in the jet evolution zone, similar to the jet node in YSO. The results provide a reference for future experimental research related to jets and contribute to a more in-depth understanding of the evolution of celestial jets.
-
Keywords:
- strong laser /
- magnetic field /
- jet
[1] Durant M, Kargaltsev O, Pavlov G G, Kropotina J, Levenfish K 2013 Astrophys. J. 763 72
Google Scholar
[2] Lu Y, Tzeferacos P, Liang E, Follett R K, Gao L, Birkel A, Froula D H, Fu W, Ji H, Lamb D, Li C K, Sio H, Petrasso R, Wei M S 2019 Phys. Plasmas 26 022902
Google Scholar
[3] Ferrari A 1998 Rev. Astron. Astrophys. 36 539
Google Scholar
[4] Soderberg A M, Kulkarni S R, Nakar E, Berger E, Cameron P B, Fox D B, Frail D, Gal-Yam D, Sari R, Cenko S B, Kasliwal M, Chevalier R A, Piran T, Price P A, Schmidt B P, Pooley G, Moon D S, Penprase B E, Ofek E, Rau A, Gehrels N, Nousek J A, Burrows D N, Persson D N, McCarthy P J 2006 Nature 442 7106
Google Scholar
[5] Lee, C F, Ho P, Li Z Y, Hirano N, Zhang Q, Shang H 2017 Nat. Astron. 1 0152
Google Scholar
[6] Hartigan P, Foster P, Wilde B H, Coker R F, Rosen P A, Hansen J F, Blue B E, Williams R J R, Carver R, Frank A 2009 Astrophys. J. 705 1073
Google Scholar
[7] Gregory C D, Howe J, Loupias B, Myers S, Notley M, Sakawa Y, Oya A, Kodama R, Keonig R, Woolsey N 2008 Astrophys. J. 676 420
Google Scholar
[8] Blandford R D, Payne D G 1982 Mon. Not. R. Astron. Soc. 199 883
Google Scholar
[9] Ferreira J 1997 Astron. Astrophys. 319 340
Google Scholar
[10] Tanaka S J, Toma K 2020 Mon. Not. R. Astron. Soc. 494 338
Google Scholar
[11] Lei Z, Zhao Z H, Yao W P, Xie Y, Jiao J L, Zhou C T, Zhu S P, He X T, Qiao B 2020 Plasma Phys. Controlled Fusion 62 095020
Google Scholar
[12] Lazzati D, Covino S, Gorosabel J, Rossi E, Zerbi F M 2004 Astron. Astrophys. 422 121
Google Scholar
[13] Ryutov D, Drake R, Kane J, Liang E, Remington B A, Wood-Vasey W M 1999 The Astrophys. J. 518 821
Google Scholar
[14] Ryutov D, Drake R, Remington B 2000 Astrophys. J. Suppl. Ser. 127 465
Google Scholar
[15] Sun W, Zhong J Y 2021 Chin. Astron. Astrophys. 45 265
Google Scholar
[16] Albertazzi B, Ciardi A, Nakatsutsumi M, Vinci T, Beard J, Bonito R, Billette J, Borghesi M, Burkley Z, Chen S N, Cowan T E, Herrmannsdorfer T, Higginson D P, Kroll F, Pikuz S A, Naughton K, Romagnani L, Riconda C, Revet G, Riquier R, Schlenvoigt H P, Skobelev I Y, Faenov A Y, Soloviev A, Huarte-Espinosa M, Frank A, Portugall O, Pepin H, Fuchs J 2014 Science 346 325
Google Scholar
[17] Yuan D W, Li Y T, Tao T, Wei H G, Zhong J Y, Zhu B J, Li Y F, Zhao J R, Li F, Han B, Zhang Z, Liang G Y, Wang F L, Hu G Y, Zheng J, Jiang S N, Du K, Ding Y K, Zhou S L, Zhu B Q, Zhu J Q, Zhao G, Zhang J 2018 Astrophys. J. 860 146
Google Scholar
[18] Li C K, Tzeferacos P, Lamb D, et al. 2016 Nat. Commun. 7 1
Google Scholar
[19] Gao L, Liang E, Lu Y, Follet R K, Sio H, Tzeferacos P, Froula D H, Birkel A, Li C K, Lamb D, Petrasso R, Fu W, Wei M, Ji H 2019 Astrophys. J. Lett. 873 L11
Google Scholar
[20] Filippov E D, Makarov S S, Burdonov K F, Yao W, Fuchs J 2021 Sci. Rep. 11 8180
Google Scholar
[21] Lei Z, Zhao Z H, Xie Y, Yuan W Q, Li L X, Gu L X, Li X Y, Zhu B Q, Zhu J Q, Zhu S P, He X T, Qiao B 2022 arXiv: 2203.06326 [physics.plasm-ph]
[22] Fryxell B, Olson K, Ricker P, Timmes F X, Zingale M, Lamb D Q, MacNeice P, Rosner R, Truran J W, Tufo H 2000 Astrophys. J. Suppl. Ser. 131 273
Google Scholar
[23] 孙伟, 安维明, 仲佳勇 2020 69 244701
Google Scholar
Sun W, An W M, Zhong J Y 2020 Acta Phys. Sin. 69 244701
Google Scholar
[24] Macfarlane J J 1989 Comput. Phys. Commun. 56 259
Google Scholar
[25] Stamper J, Ripi B 1975 Phys. Rev. Lett. 34 138
Google Scholar
[26] Biermann L 1950 Zeitschrift Naturforschung Teil A 5 65
Google Scholar
[27] Doi K, Susa H 2011 Astrophys. J. 741 93
Google Scholar
-
图 1 激光驱动CH平面靶产生喷流的初始模拟布置图
Figure 1. Initial simulated setup for generating jet using a laser-driven CH flat-target
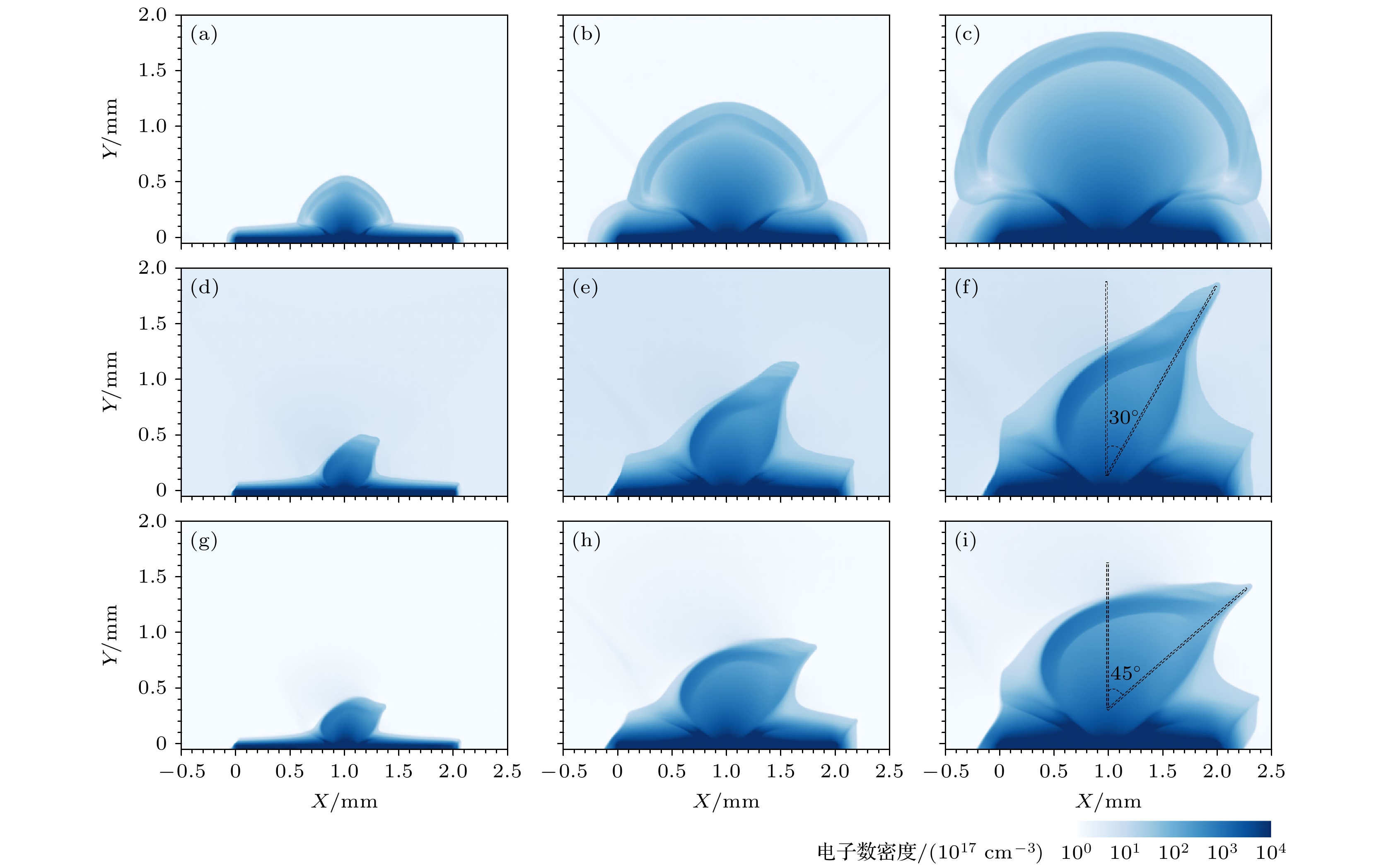
图 2 不同时刻下的电子密度分布, 不同列对应不同时刻, 分别为2.5, 5和7.5 ns; 不同行对应不同磁场情况, 其中(a)—(c)无磁场情况; (d)—(f)
$ \alpha=30^{\circ} $ , 初始外加20 T磁场情况; (g)—(i)$ \alpha=45^{\circ} $ , 初始外加20 T磁场情况Figure 2. Snapshots of the electron density distribution at different times. Different columns correspond to different times, 2.5, 5 and 7.5 ns respectively. Different rows correspond to different magnetic fields: (a)–(c) Non-magnetic fields; (d)–(f)
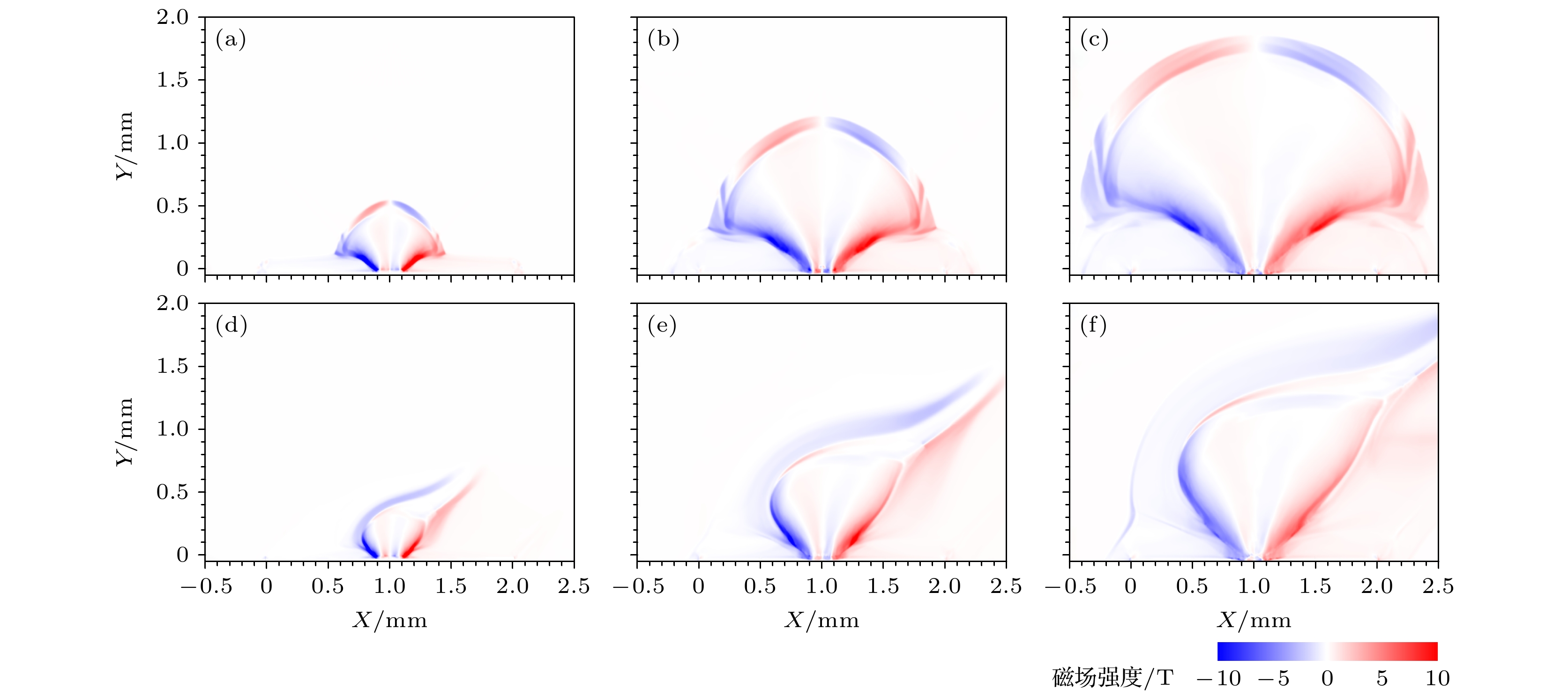
$ \alpha=30^{\circ} $ with 20 T; (g)–(i)$ \alpha=45^{\circ} $ with 20 T
图 3 Biermann自生磁场的强度分布情况, 不同行表征不同外加磁场情况, 不同列代表不同时刻(2.5, 5, 7.5 ns) (a)—(c)无外加磁场; (d)—(f)
$ \alpha=30^{\circ} $ , 初始外加20 T磁场情况Figure 3. Snapshots of the distribution of of Biermann self-generated magnetic field. Different rows represent different applied magnetic field conditions, and different columns represent different times (2.5, 5, 7.5 ns): (a)–(c) Absence of an applied magnetic field; (d)–(f)
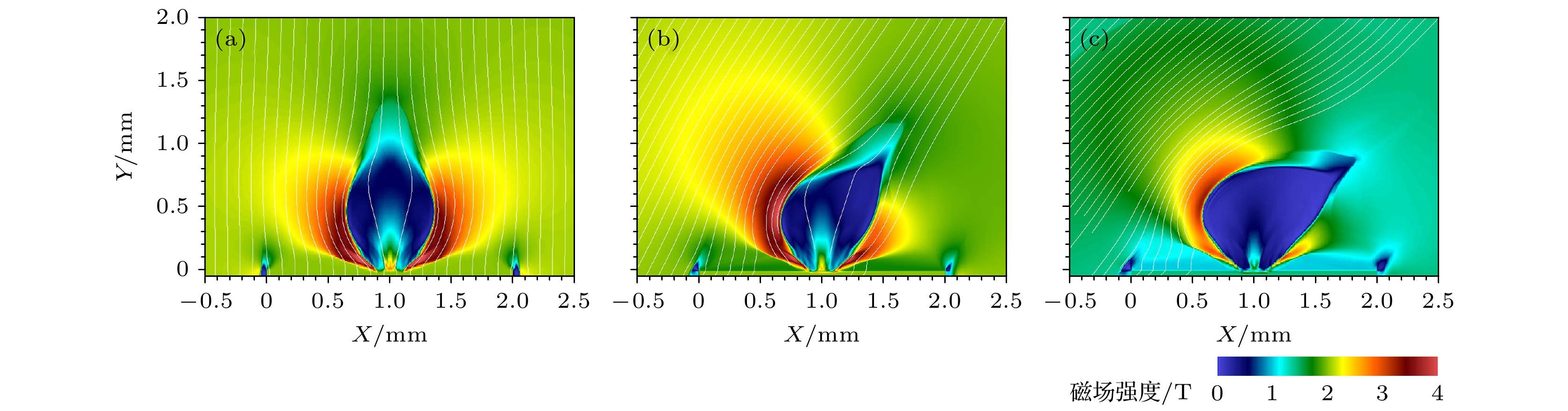
$ \alpha=30^{\circ} $ and an initial magnetic field of 20 T applied
图 4
$t=5\; {\rm{ns}}$ 时刻外加磁场强度分布 (a)$ \alpha=0^{\circ} $ ; (b)$ \alpha=30^{\circ} $ ; (c)$ \alpha=45^{\circ} $ Figure 4. Distribution of applied magnetic field strength at
$t=5 \;{\rm{ns}}$ . (a), (b) and (c) respectively correspond to$ \alpha=0^{\circ} $ ,$ \alpha=30^{\circ} $ and$ \alpha=45^{\circ} $ case
图 5 α =
$ 0^{\circ} $ 、初始外加20 T磁场条件下, 不同时刻的电子密度分布情况 (a)—(d)分别对应10, 15, 20和25 nsFigure 5. Snapshots of the electron density distribution at the different times under the condition of α =
$ 0^{\circ} $ and initial applied 20 T: (a)–(d) corresponds to 10, 15, 20 and 25 ns respectively
图 6
$ \alpha=0^{\circ} $ 、初始外加20 T磁场条件下, 不同时刻的磁场强度分布 (a)—(d)分别对应10, 15, 20和25 nsFigure 6. Distribution of applied magnetic field at different times under the condition of
$ \alpha=0^{\circ} $ and initial applied 20 T magnetic field: (a)–(d) corresponds to 10, 15, 20 and 25 ns respectively
图 7
$ \alpha=0^{\circ} $ 、初始外加20 T磁场条件下,$ t=10\ {\rm{ns}} $ 时(a)热压、(b)磁压、(c)冲压强度分布情况Figure 7. Under the condition of
$ \alpha=0^{\circ} $ and initial applied 20 T magnetic field, the distribution of (a) hot pressure, (b) magnetic pressure and (c) stamping strength at$t=10\; {\rm{ns}}$ 
图 8
$ \alpha=0^{\circ} $ 时, 初始外加20 T磁场条件下,$ t=10\; {\rm{ns}} $ 时刻下, x-y平面内$ y=2\; {\rm{mm}} $ 范围的等离子体磁压、热压、冲压的对比情况Figure 8. Comparison of plasma magnetic pressure, hot pressing and the ram pressure within the range of y = 2 mm in the x-y plane at the time of
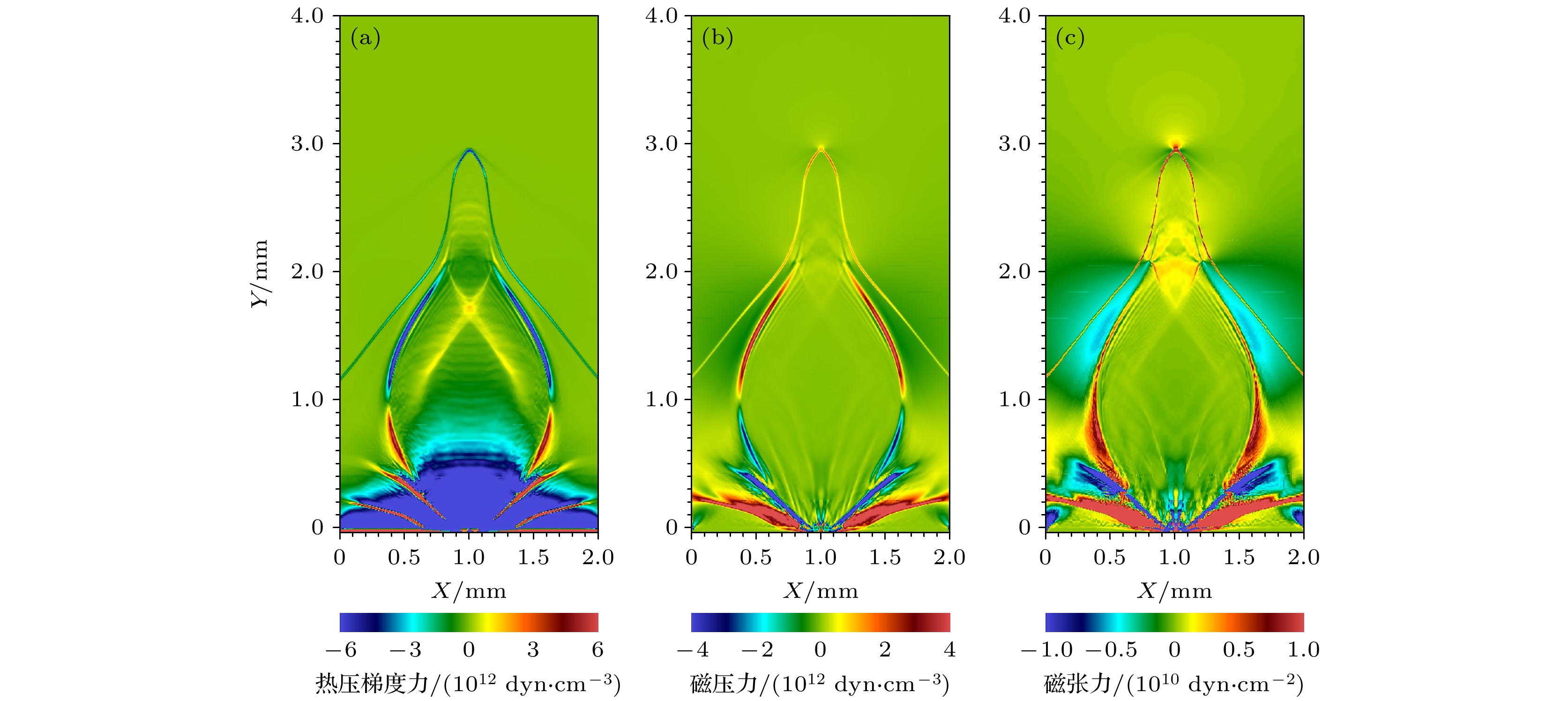
$ t=10\; {\rm{ns}} $ under the condition of$ \alpha=0^{\circ} $ and initial applied 20 T magnetic field
图 9
$ \alpha=0^{\circ} $ 时, 初始外加20 T磁场条件下,$t=10\; {\rm{ns}}$ 时刻下, (a)热力梯度力、(b)磁压力、(c)磁张力的矢量分布Figure 9. Vector distribution of (a) thermal gradient force, (b) magnetic pressure and (c) magnetic tension at the time of
$t=10\; {\rm{ns}}$ under the condition of$ \alpha=0^{\circ} $ and initial applied 20 T magnetic field
图 10 喷流长径比随时间的变化情况
Figure 10. Change of jet length-diameter ratio with time
-
[1] Durant M, Kargaltsev O, Pavlov G G, Kropotina J, Levenfish K 2013 Astrophys. J. 763 72
Google Scholar
[2] Lu Y, Tzeferacos P, Liang E, Follett R K, Gao L, Birkel A, Froula D H, Fu W, Ji H, Lamb D, Li C K, Sio H, Petrasso R, Wei M S 2019 Phys. Plasmas 26 022902
Google Scholar
[3] Ferrari A 1998 Rev. Astron. Astrophys. 36 539
Google Scholar
[4] Soderberg A M, Kulkarni S R, Nakar E, Berger E, Cameron P B, Fox D B, Frail D, Gal-Yam D, Sari R, Cenko S B, Kasliwal M, Chevalier R A, Piran T, Price P A, Schmidt B P, Pooley G, Moon D S, Penprase B E, Ofek E, Rau A, Gehrels N, Nousek J A, Burrows D N, Persson D N, McCarthy P J 2006 Nature 442 7106
Google Scholar
[5] Lee, C F, Ho P, Li Z Y, Hirano N, Zhang Q, Shang H 2017 Nat. Astron. 1 0152
Google Scholar
[6] Hartigan P, Foster P, Wilde B H, Coker R F, Rosen P A, Hansen J F, Blue B E, Williams R J R, Carver R, Frank A 2009 Astrophys. J. 705 1073
Google Scholar
[7] Gregory C D, Howe J, Loupias B, Myers S, Notley M, Sakawa Y, Oya A, Kodama R, Keonig R, Woolsey N 2008 Astrophys. J. 676 420
Google Scholar
[8] Blandford R D, Payne D G 1982 Mon. Not. R. Astron. Soc. 199 883
Google Scholar
[9] Ferreira J 1997 Astron. Astrophys. 319 340
Google Scholar
[10] Tanaka S J, Toma K 2020 Mon. Not. R. Astron. Soc. 494 338
Google Scholar
[11] Lei Z, Zhao Z H, Yao W P, Xie Y, Jiao J L, Zhou C T, Zhu S P, He X T, Qiao B 2020 Plasma Phys. Controlled Fusion 62 095020
Google Scholar
[12] Lazzati D, Covino S, Gorosabel J, Rossi E, Zerbi F M 2004 Astron. Astrophys. 422 121
Google Scholar
[13] Ryutov D, Drake R, Kane J, Liang E, Remington B A, Wood-Vasey W M 1999 The Astrophys. J. 518 821
Google Scholar
[14] Ryutov D, Drake R, Remington B 2000 Astrophys. J. Suppl. Ser. 127 465
Google Scholar
[15] Sun W, Zhong J Y 2021 Chin. Astron. Astrophys. 45 265
Google Scholar
[16] Albertazzi B, Ciardi A, Nakatsutsumi M, Vinci T, Beard J, Bonito R, Billette J, Borghesi M, Burkley Z, Chen S N, Cowan T E, Herrmannsdorfer T, Higginson D P, Kroll F, Pikuz S A, Naughton K, Romagnani L, Riconda C, Revet G, Riquier R, Schlenvoigt H P, Skobelev I Y, Faenov A Y, Soloviev A, Huarte-Espinosa M, Frank A, Portugall O, Pepin H, Fuchs J 2014 Science 346 325
Google Scholar
[17] Yuan D W, Li Y T, Tao T, Wei H G, Zhong J Y, Zhu B J, Li Y F, Zhao J R, Li F, Han B, Zhang Z, Liang G Y, Wang F L, Hu G Y, Zheng J, Jiang S N, Du K, Ding Y K, Zhou S L, Zhu B Q, Zhu J Q, Zhao G, Zhang J 2018 Astrophys. J. 860 146
Google Scholar
[18] Li C K, Tzeferacos P, Lamb D, et al. 2016 Nat. Commun. 7 1
Google Scholar
[19] Gao L, Liang E, Lu Y, Follet R K, Sio H, Tzeferacos P, Froula D H, Birkel A, Li C K, Lamb D, Petrasso R, Fu W, Wei M, Ji H 2019 Astrophys. J. Lett. 873 L11
Google Scholar
[20] Filippov E D, Makarov S S, Burdonov K F, Yao W, Fuchs J 2021 Sci. Rep. 11 8180
Google Scholar
[21] Lei Z, Zhao Z H, Xie Y, Yuan W Q, Li L X, Gu L X, Li X Y, Zhu B Q, Zhu J Q, Zhu S P, He X T, Qiao B 2022 arXiv: 2203.06326 [physics.plasm-ph]
[22] Fryxell B, Olson K, Ricker P, Timmes F X, Zingale M, Lamb D Q, MacNeice P, Rosner R, Truran J W, Tufo H 2000 Astrophys. J. Suppl. Ser. 131 273
Google Scholar
[23] 孙伟, 安维明, 仲佳勇 2020 69 244701
Google Scholar
Sun W, An W M, Zhong J Y 2020 Acta Phys. Sin. 69 244701
Google Scholar
[24] Macfarlane J J 1989 Comput. Phys. Commun. 56 259
Google Scholar
[25] Stamper J, Ripi B 1975 Phys. Rev. Lett. 34 138
Google Scholar
[26] Biermann L 1950 Zeitschrift Naturforschung Teil A 5 65
Google Scholar
[27] Doi K, Susa H 2011 Astrophys. J. 741 93
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 3547
- PDF Downloads: 130
- Cited By: 0
