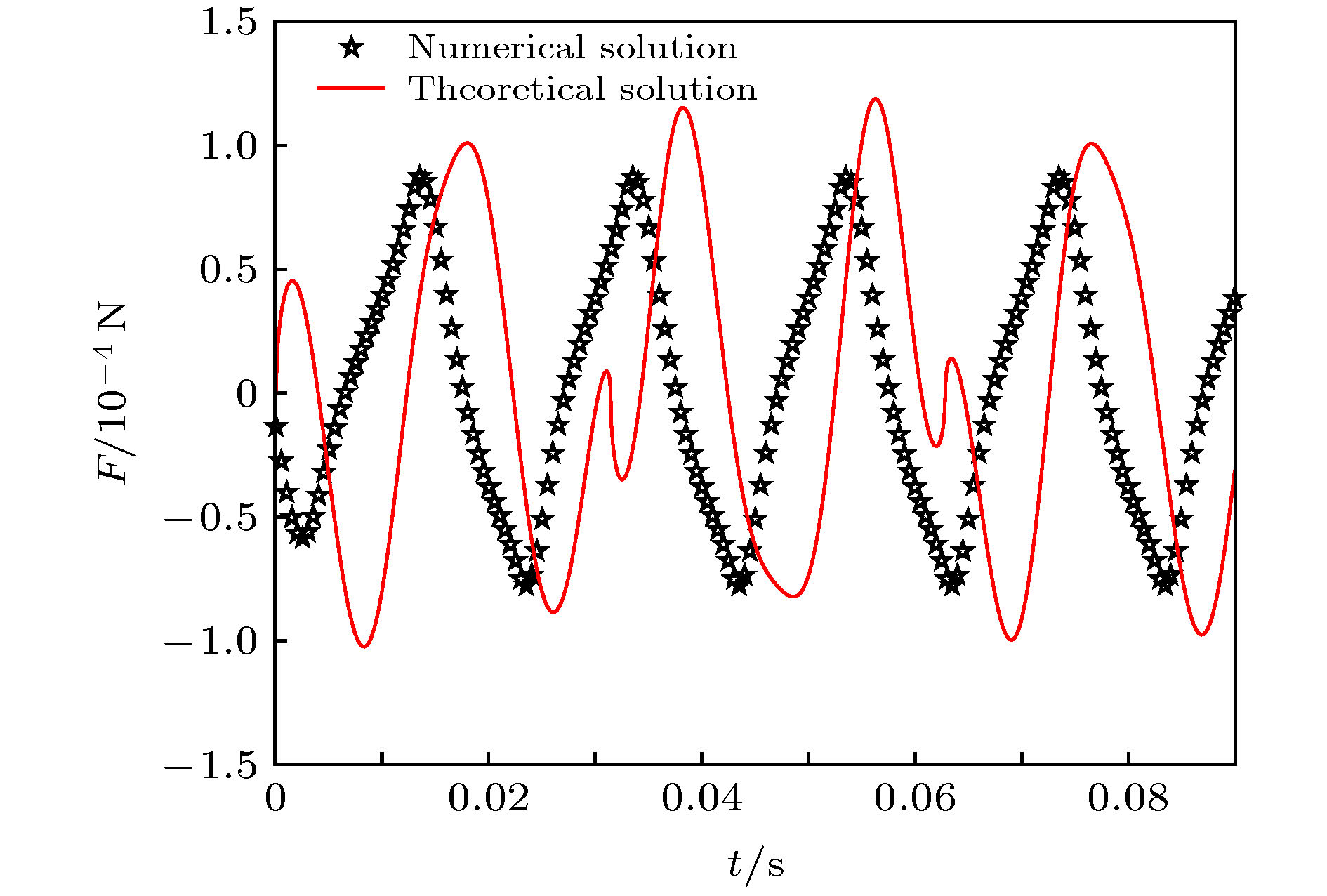
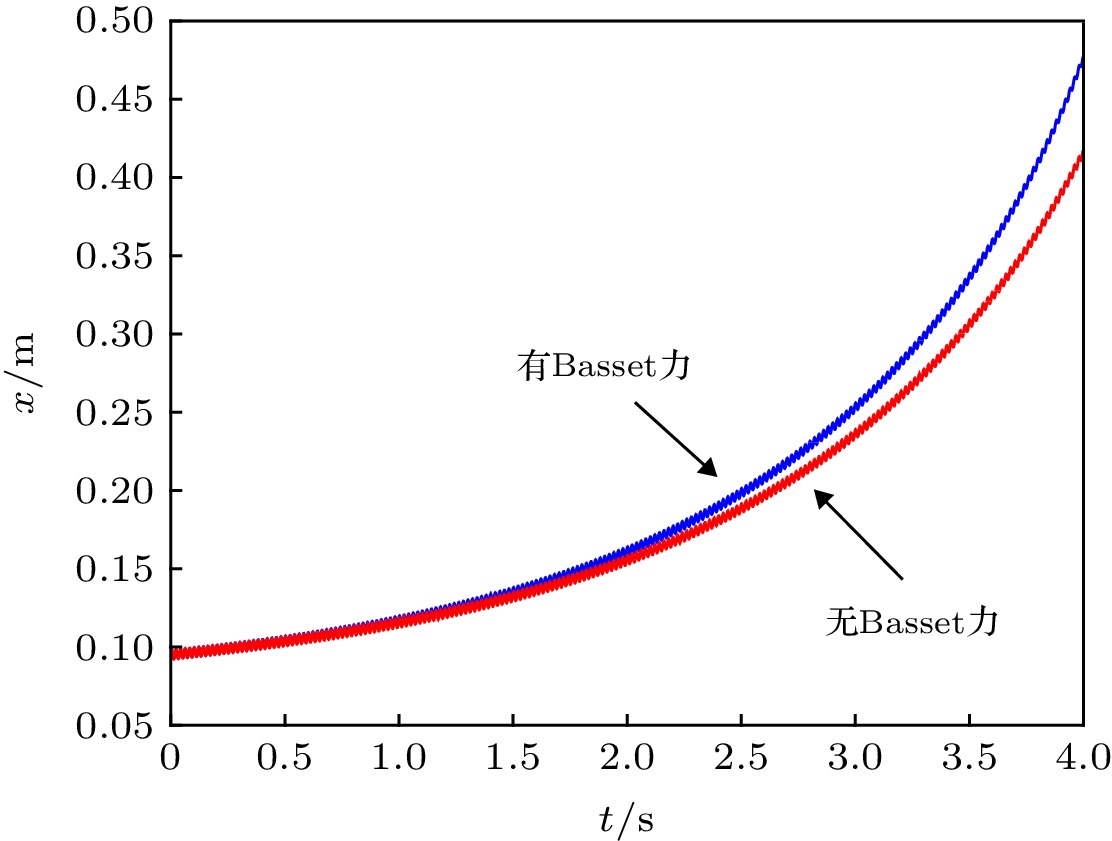
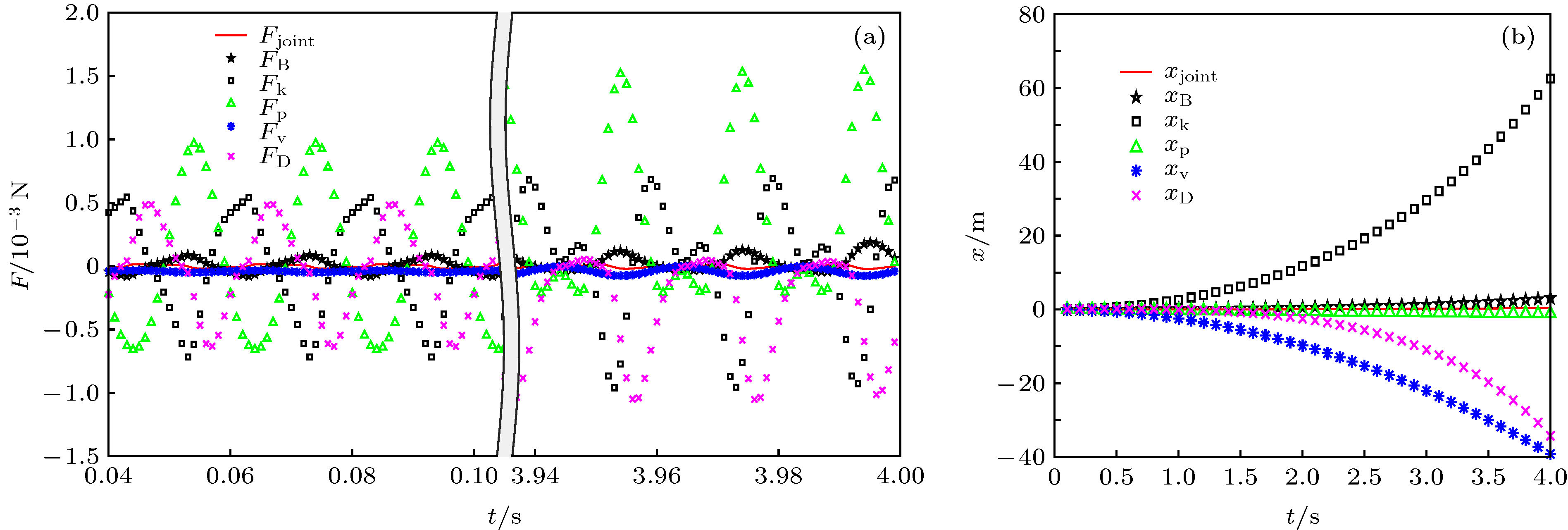
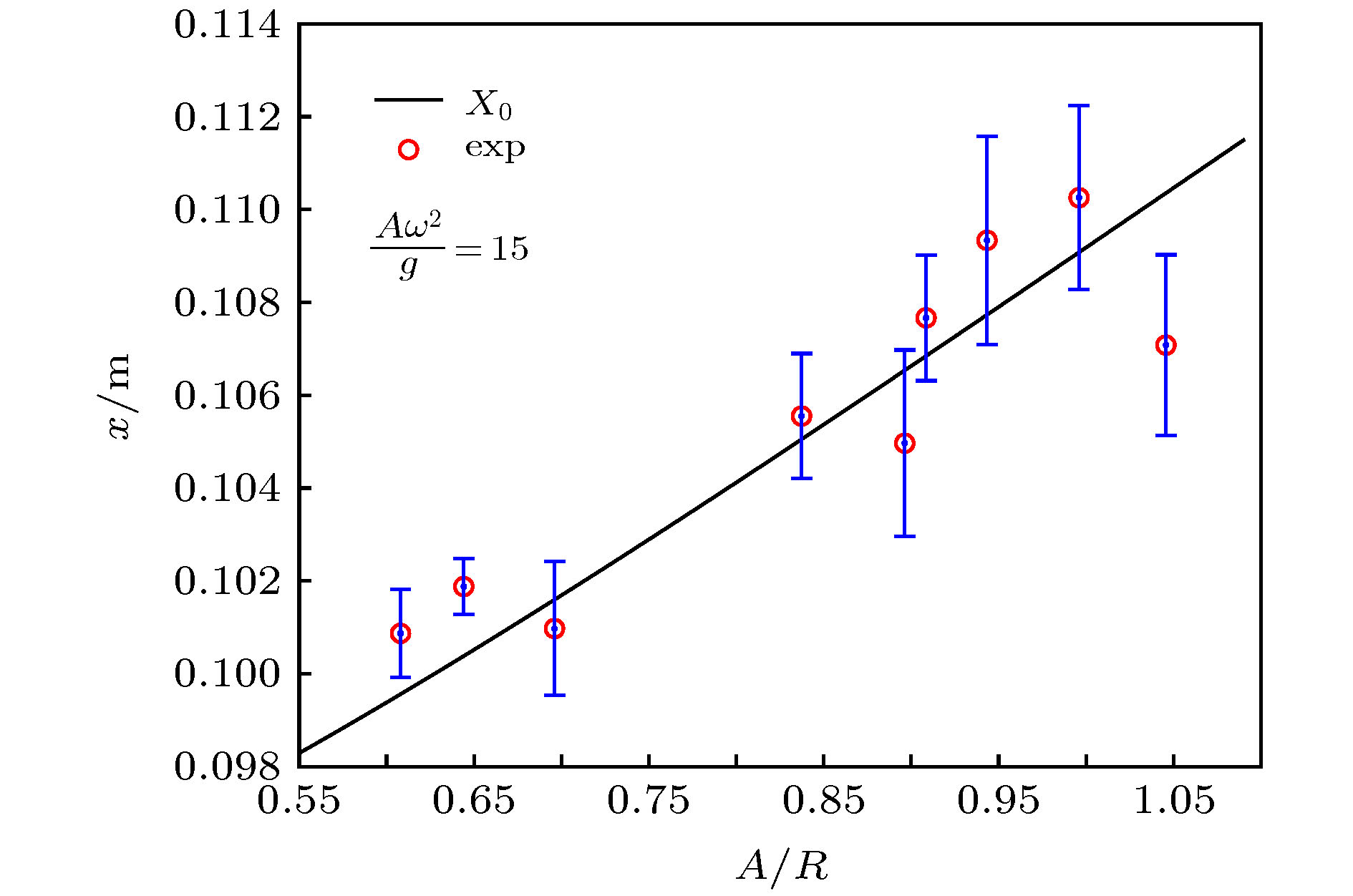
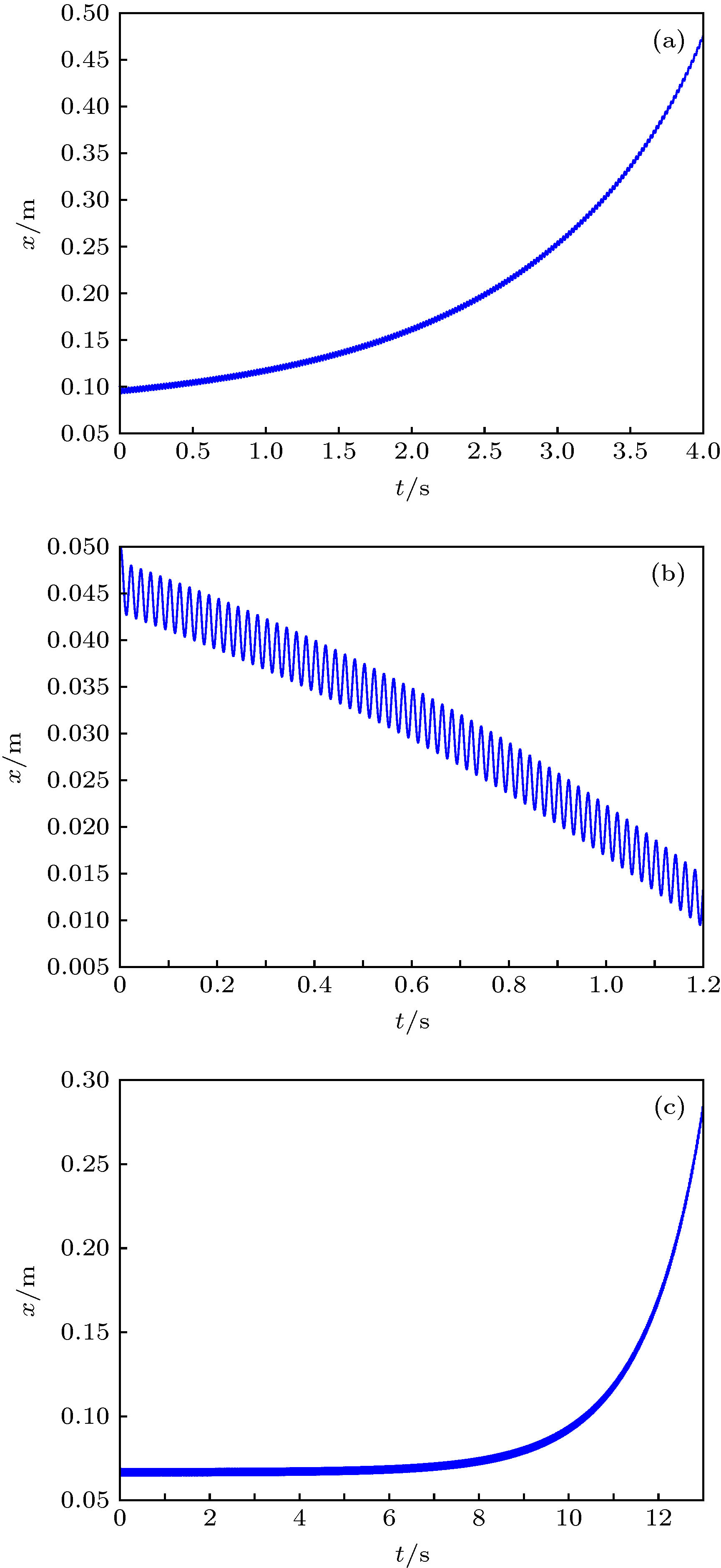
-
When a container filled with water is subjected to vertical vibration, bubbles in the water may sink. This phenomenon exists widely in the field of engineering, and has a non-negligible influence on aerospace engineering and ship engineering. Therefore, it is of great significance to study the movement of bubble sinking in order to reduce the adverse effect caused by bubble sinking in the project. In previous papers, the effect of Basset force on bubble motion was usually ignored. In this paper, the bubble motion model based on the ideal gas equation is built for spherical bubbles, and the influence of the Basset force on the bubble motion is considered in the model. In the process of solving Basset force, the motion is directly separated and the convergence factor is introduced in theoretical solution. The equal step composite trapezoid formula is applied to the numerical solution. The results of numerical calculation show that the added mass force is important for bubble sinking. We find that the Basset force has no effect on the stable oscillation position of bubble, but it can accelerate the later trajectory of bubble motion. Importantly, we demonstrate that the bubble is hindered by the following component forces: buoyancy, viscous resistance, and flow thrust (which are ordered from large to small value). The movement of the bubble is observed to be in the form of oscillation, and there exists a depth, i.e. a critical depth: the bubble oscillate steadily at this depth, specifically, the bubble rises above this depth and sinks below this depth. When the vibration pressure changes, the location of the bubble’s stable oscillation will also be affected. The origin can be ascribed to the change of added mass force caused by the change of vibration pressure. Meanwhile, on the basis of digital image processing method, denoising, filtering, local stretching, image binarization and image filling are used to extract the characteristic dimension of bubbles. The theoretical value of the critical depth of bubble sinking matches the experimental result and their relative error is less than 5%. These new findings enrich the understanding of the moving bubbles in liquid materials used in nuclear reactors, rocket propulsion fuels and chemical experiments.
-
Keywords:
- vertical vibration /
- bubble sinking /
- stable oscillation /
- Basset force
[1] Buchanan R H, Jameson G, Oedjoe D 1962 Ind. Eng. Chem. Fundam. 1 82
Google Scholar
[2] Bleich H H 1956 Jet Propul. 26 958
Google Scholar
[3] Brennen C E 1982 A Review of Added Mass and Fluid Inertial Forces (Port Hueneme: Naval Civil Engineering Laboratory) pp2−6
[4] Sorokin V S, Blekhman I I, Vasilkov V B 2012 Nonlinear Dyn. 67 147
Google Scholar
[5] Ellenberger J, Krishna R 2007 Chem. Eng. Sci. 62 5669
Google Scholar
[6] Ellenberger J, Krishna R 2007 Chem. Eng. Sci. 62 7548
Google Scholar
[7] Baird M H I 1963 Can. J. Chem. Eng. 41 52
Google Scholar
[8] Blekhman I I, Blekhman L I, Vaisberg L A, Vasil’Kov V B, Yakimova K S 2008 Dokl. Phys. 53 520
Google Scholar
[9] Crum L A, Eller A I 1970 J. Acoust. Soc. Am. 48 181
Google Scholar
[10] Sorokin V S, Blekhman I I, Blekhman L I, Vasilkov V B, Yakimova K S 2011 The 10 th International Conference on Vibration Problems Prague, Czech Republic, September 5–8, 2011 pp127−132
[11] Blekhman I I, Blekhman L I, Sorokin V S, Vaisberg L A, Vasilkov V B, Yakimova K S 2013 Procedia IUTAM 8 43
Google Scholar
[12] Sorokin V, Blekhman I I, Thomsen J J 2010 Nonlinear Dyn. 60 639
Google Scholar
[13] Houghton G 1963 Proc. R. Soc. Lond. A 272 33
Google Scholar
[14] 李双 2018 硕士学位论文 (杭州: 浙江大学)
Li S 2018 M. S. Thesis (Hangzhou: Zhejiang University) (in Chinese)
[15] Zoueshtiagh F, Caps H, Legendre M, Vandewalle N, Petitjeans P, Kurowski P 2006 Eur. Phys. J. E 20 317
Google Scholar
[16] 田恒斗, 金良安, 迟卫, 房毅, 韩云东, 王涌 2011 力学学报 43 680
Google Scholar
Tian H D, Jin L A, Chi W, Fang Y, Han Y D, Wang Y 2011 Chin. J. Theor. Appl. Mech. 43 680
Google Scholar
[17] 黄社华, 程良骏 1996 水利学报 54
Google Scholar
Huang S H, Cheng L J 1996 J. Hydraul. Eng. 54
Google Scholar
[18] 李帅, 孙龙泉, 张阿漫 2014 63 184701
Google Scholar
Li S, Sun L Q, Zhang A M 2014 Acta Phys. Sin. 63 184701
Google Scholar
[19] 田恒斗, 金良安, 丁兆红, 谢田华 2010 化工学报 61 15
Google Scholar
Tian H D, Jin L A, Ding Z H, Xie T H 2010 CIESC J. 61 15
Google Scholar
[20] 马艳, 林书玉, 徐洁 2018 67 034301
Google Scholar
Ma Y, Lin S Y, Xu J 2018 Acta Phys. Sin. 67 034301
Google Scholar
[21] 沈壮志, 林书玉 2011 60 104302
Google Scholar
Shen Z Z, Lin S Y 2011 Acta Phys. Sin. 60 104302
Google Scholar
[22] 张鹏利, 林书玉, 朱华泽, 张涛 2019 68 134301
Google Scholar
Zhang P L, Lin S Y, Zhu H Z, Zhang T 2019 Acta Phys. Sin. 68 134301
Google Scholar
[23] Tadaki T, Maeda S 1961 Chem. Eng. 25 254
Google Scholar
[24] 刘柳 2013 硕士学位论文 (长沙: 中南大学)
Liu L 2013 M. S. Thesis (Changsha: Central South University) (in Chinese)
[25] Zawala J 2016 Phys Fluids. 28 057103
Google Scholar
[26] 王红一 2011 博士学位论文 (天津: 天津大学)
Wang H Y 2011 Ph. D. Dissertation (Tianjin: Tianjin University) (in Chinese)
[27] Flanders H 1982 Am. Math. Mon. 89 264
Google Scholar
[28] 曲伟杰 2009 硕士学位论文 (天津: 天津大学)
Qu W J 2009 M. S. Thesis (Tianjin: Tianjin University) (in Chinese)
[29] Mi kaelian D, Larcy A, Dehaeck S, Haut B 2013 Chem. Eng. Sci. 100 529
Google Scholar
[30] Keshavarzi G, Pawell R S, Barber T J, Yeoh G H 2014 Chem. Eng. Sci. 112 25
Google Scholar
[31] 汤华鹏, 温济铭, 谷海峰 2019 应用科技 46 108
Google Scholar
Tang H P, Wen J M, Gu H F 2019 Appl. Sci. Technol. 46 108
Google Scholar
-
图 1 气泡运动方程的数值模拟 (a) 气泡初始位置为0.1 m; (b) 气泡初始位置为0.05 m; (c) 气泡初始位置为0.076 m
Figure 1. Numerical simulation of the bubble motion equation
$ : $ (a) The initial position of the bubble is 0.1 m; (b) the initial position of the bubble is 0.05 m; (c) the initial position of the bubble is 0.076 m.
图 2 Basset力解析解和数值解的比较
Figure 2. Comparison between the analytical and numerical solutions of Basset forces.
图 3 Basset力对气泡运动方程的影响
Figure 3. Effect of Basset force on the equation of motion of bubbles.
图 4 气泡受力分析 (a)气泡下沉前期和后期各个分力的对比; (b) 气泡分力对气泡位移的贡献
Figure 4. Force analysis of bubble: (a) Comparison of component forces in the early and late stages of bubble sinking; (b) contribution of bubble component force to bubble displacement.
图 5 实验仪器 (a)振动台和瓶子; (b)功率放大器; (c)信号示波器
Figure 5. Experimental instrument: (a) Shaker and bottle; (b) power amplifier; (c) signal oscilloscope.
图 6 气泡图像处理 (a)背景图像; (b)带有气泡的图像; (c)差影法处理; (d)截取带有气泡的局部图像; (e)去噪; (f)
$3 \times 3$ 滤波; (g)局部拉伸; (h)二值化处理; (i)填充图像Figure 6. Bubble image processing: (a) Background image; (b) image with bubbles; (c) subtraction processing; (d) local image with bubbles; (e) denoising; (f)
$3 \times 3$ filtering; (g) local stretching; (h) image binarization; (i) image filling.
图 7 理论值与实际值的对比
Figure 7. Comparison between theoretical value and actual value.
-
[1] Buchanan R H, Jameson G, Oedjoe D 1962 Ind. Eng. Chem. Fundam. 1 82
Google Scholar
[2] Bleich H H 1956 Jet Propul. 26 958
Google Scholar
[3] Brennen C E 1982 A Review of Added Mass and Fluid Inertial Forces (Port Hueneme: Naval Civil Engineering Laboratory) pp2−6
[4] Sorokin V S, Blekhman I I, Vasilkov V B 2012 Nonlinear Dyn. 67 147
Google Scholar
[5] Ellenberger J, Krishna R 2007 Chem. Eng. Sci. 62 5669
Google Scholar
[6] Ellenberger J, Krishna R 2007 Chem. Eng. Sci. 62 7548
Google Scholar
[7] Baird M H I 1963 Can. J. Chem. Eng. 41 52
Google Scholar
[8] Blekhman I I, Blekhman L I, Vaisberg L A, Vasil’Kov V B, Yakimova K S 2008 Dokl. Phys. 53 520
Google Scholar
[9] Crum L A, Eller A I 1970 J. Acoust. Soc. Am. 48 181
Google Scholar
[10] Sorokin V S, Blekhman I I, Blekhman L I, Vasilkov V B, Yakimova K S 2011 The 10 th International Conference on Vibration Problems Prague, Czech Republic, September 5–8, 2011 pp127−132
[11] Blekhman I I, Blekhman L I, Sorokin V S, Vaisberg L A, Vasilkov V B, Yakimova K S 2013 Procedia IUTAM 8 43
Google Scholar
[12] Sorokin V, Blekhman I I, Thomsen J J 2010 Nonlinear Dyn. 60 639
Google Scholar
[13] Houghton G 1963 Proc. R. Soc. Lond. A 272 33
Google Scholar
[14] 李双 2018 硕士学位论文 (杭州: 浙江大学)
Li S 2018 M. S. Thesis (Hangzhou: Zhejiang University) (in Chinese)
[15] Zoueshtiagh F, Caps H, Legendre M, Vandewalle N, Petitjeans P, Kurowski P 2006 Eur. Phys. J. E 20 317
Google Scholar
[16] 田恒斗, 金良安, 迟卫, 房毅, 韩云东, 王涌 2011 力学学报 43 680
Google Scholar
Tian H D, Jin L A, Chi W, Fang Y, Han Y D, Wang Y 2011 Chin. J. Theor. Appl. Mech. 43 680
Google Scholar
[17] 黄社华, 程良骏 1996 水利学报 54
Google Scholar
Huang S H, Cheng L J 1996 J. Hydraul. Eng. 54
Google Scholar
[18] 李帅, 孙龙泉, 张阿漫 2014 63 184701
Google Scholar
Li S, Sun L Q, Zhang A M 2014 Acta Phys. Sin. 63 184701
Google Scholar
[19] 田恒斗, 金良安, 丁兆红, 谢田华 2010 化工学报 61 15
Google Scholar
Tian H D, Jin L A, Ding Z H, Xie T H 2010 CIESC J. 61 15
Google Scholar
[20] 马艳, 林书玉, 徐洁 2018 67 034301
Google Scholar
Ma Y, Lin S Y, Xu J 2018 Acta Phys. Sin. 67 034301
Google Scholar
[21] 沈壮志, 林书玉 2011 60 104302
Google Scholar
Shen Z Z, Lin S Y 2011 Acta Phys. Sin. 60 104302
Google Scholar
[22] 张鹏利, 林书玉, 朱华泽, 张涛 2019 68 134301
Google Scholar
Zhang P L, Lin S Y, Zhu H Z, Zhang T 2019 Acta Phys. Sin. 68 134301
Google Scholar
[23] Tadaki T, Maeda S 1961 Chem. Eng. 25 254
Google Scholar
[24] 刘柳 2013 硕士学位论文 (长沙: 中南大学)
Liu L 2013 M. S. Thesis (Changsha: Central South University) (in Chinese)
[25] Zawala J 2016 Phys Fluids. 28 057103
Google Scholar
[26] 王红一 2011 博士学位论文 (天津: 天津大学)
Wang H Y 2011 Ph. D. Dissertation (Tianjin: Tianjin University) (in Chinese)
[27] Flanders H 1982 Am. Math. Mon. 89 264
Google Scholar
[28] 曲伟杰 2009 硕士学位论文 (天津: 天津大学)
Qu W J 2009 M. S. Thesis (Tianjin: Tianjin University) (in Chinese)
[29] Mi kaelian D, Larcy A, Dehaeck S, Haut B 2013 Chem. Eng. Sci. 100 529
Google Scholar
[30] Keshavarzi G, Pawell R S, Barber T J, Yeoh G H 2014 Chem. Eng. Sci. 112 25
Google Scholar
[31] 汤华鹏, 温济铭, 谷海峰 2019 应用科技 46 108
Google Scholar
Tang H P, Wen J M, Gu H F 2019 Appl. Sci. Technol. 46 108
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 6274
- PDF Downloads: 149
- Cited By: 0
