Theoretical calculations of stabilities and properties of transition metal borocarbides TM3B3C and TM4B3C2 compound

Hu Qian-Ku; Hou Yi-Ming; Wu Qing-Hua; Qin Shuang-Hong; Wang Li-Bo; Zhou Ai-Guo

doi:10.7498/aps.68.20190158

Abstract

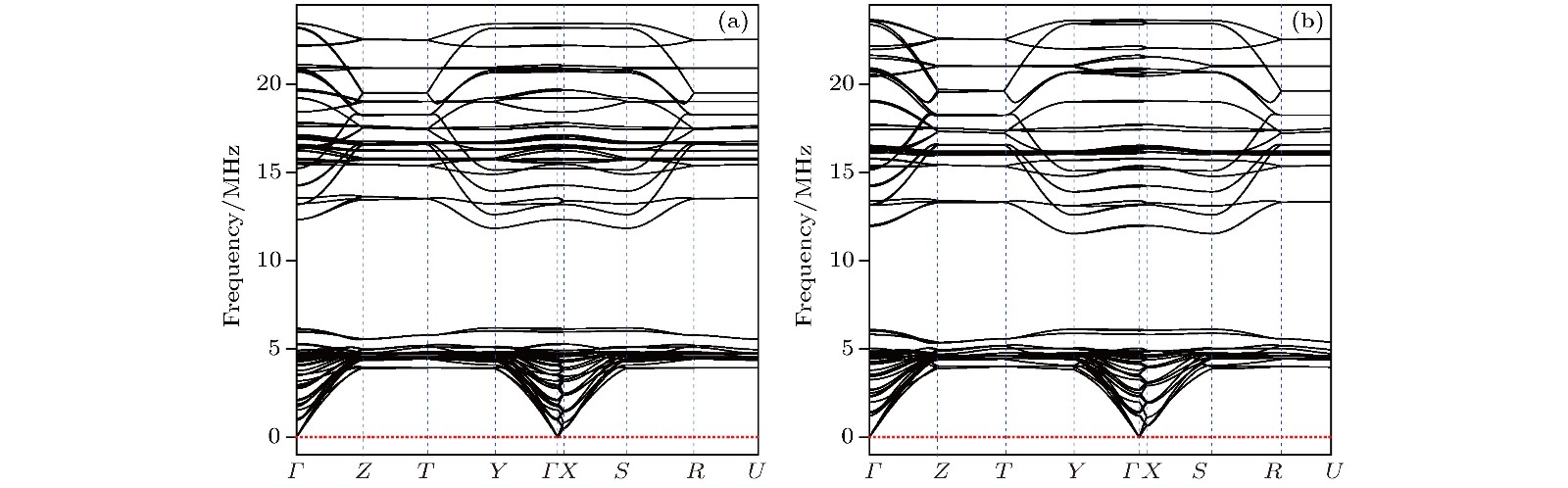
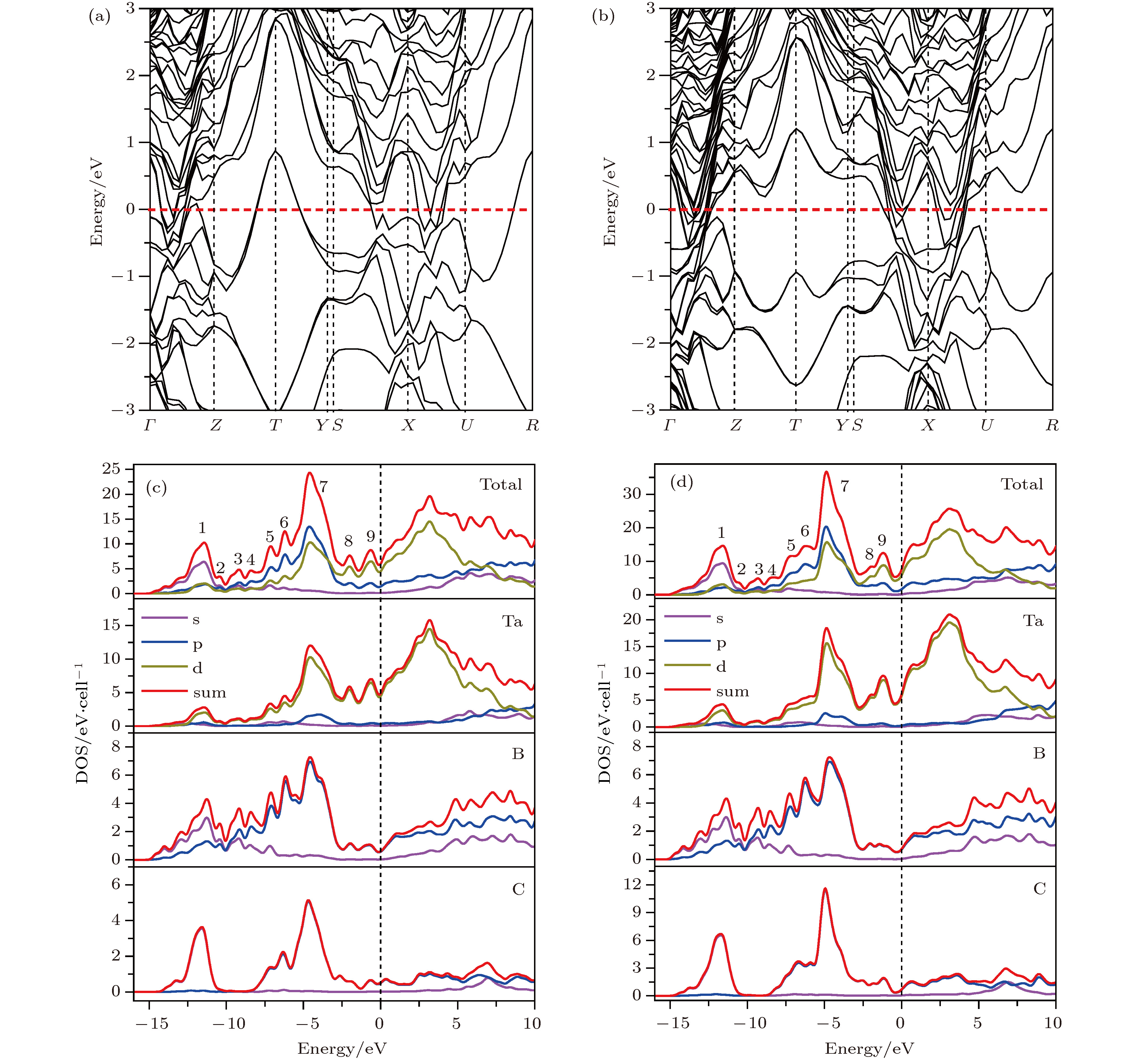
To search new hard or superhard materials in transition-metal light-element compounds is a current research focus. Most of the past researches focused on binary phases such as transition metal borides, carbides and nitrides, while the researches on ternary phases were relatively rare. The single crystals Nb₃B₃C and Nb₄B₃C₂ were synthesized recently by using Al-Cu alloys as auxiliary metals and their structures were determined by Hillebrechtand Gebhardt. In the present paper, 29 TM₃B₃C and 29 TM₄B₃C₂ configurations are constructed by TM atoms (TM = Sc to Zn, Y to Cd, Hf to Hg) replacing Nb atoms in the known Nb₃B₃C and Nb₄B₃C₂ configuration. By calculating the formation energy from first-principles density functional theories, only 13 TM₃B₃C and 11 TM₄B₃C₂ phases are stable compared with the three elemental substances of TM, boron and carbon. However compared with the most competing phases, only Ta₃B₃C, Nb₃B₃C and Nb₄B₃C₂ phases are stable thermodynamically. The metastable Ta₄B₃C₂ phase at 0 K becomes stable when temperature is higher than 250 K. Thus two new phases of Ta₃B₃C and Ta₄B₃C₂ are uncovered to be stable thermodynamically. Global structure searches conducted by the popular USPEX and CALYPSO softwares prove the Ta₃B₃C and Ta₄B₃C₂ phases to be the most favorable energetically. By calculating the phonon dispersion curves of the Ta₃B₃C and Ta₄B₃C₂ phase, no imaginary phonon frequencies are observed in the whole Brillouin zone, which demonstrates the dynamical stability of the Ta₃B₃C and Ta₄B₃C₂ phase. The calculated elastic constant of the Ta₃B₃C and Ta₄B₃C₂ phases satisfy the criteria of mechanical stability, showing that the Ta₃B₃C and Ta₄B₃C₂ phase are stable mechanically. The calculations of band structure and density of state show that the Ta₃B₃C and Ta₄B₃C₂ phases are both conducting, which mainly arises from the d electrons of Ta atoms. The calculated bulk modulus and shear modulus of the Ta₃B₃C and Ta₄B₃C₂ phases show their brittle nature. The hardness of Ta₃B₃C and Ta₄B₃C₂ phase are nearly the same and calculated to be about 26 GPa by Chen’s and Tian’s models, which illuminates that the two phases are hard but not superhard.

Keywords:

Authors and contacts

1.
School of Materials Science and Engineering, Henan Key Laboratory of Materials on Deep-Earth Science and Technology, Henan Polytechnic University, Jiaozuo 454000, China
2.
State Key Laboratory of Metastable Materials Science and Technology, Yanshan University, Qinhuangdao 066004, China

Corresponding author: Hu Qian-Ku, hqk@hpu.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 51472075, 51772077), the Program for Innovative Research Team (in Science and Technology) in the University of Henan Province, China (Grant No. 19IRTSTHN027), and the Natural Science Foundation of Henan Province, China (Grant Nos. 182300410228, 182300410275).

FullText HTML : translate this paragraph

References

[1]	Tian Y J, Xu B, Zhao Z S 2012 Int. J. Refract. Met. Hard Mat. 33 93 Google Scholar
[2]	包括, 马帅领, 徐春红, 崔田 2017 66 036104 Google Scholar Bao K, Ma S L, Xu C H, Cui T 2017 Acta Phys. Sin. 66 036104 Google Scholar
[3]	Zhou X F, Sun J, Fan Y X, Chen J, Wang H T, Guo X J, He J L, Tian Y J 2007 Phys. Rev. B 76 100101 Google Scholar
[4]	Dong H F, Oganov A R, Wang Q G, Wang S N, Wang Z H, Zhang J, Esfahani M M D, Zhou X F, Wu F G, Zhu Q 2016 Sci. Rep. 6 31288 Google Scholar
[5]	Tian Y J, Xu B, Yu D L, Ma Y M, Wang Y B, Jiang Y B, Hu W T, Tang C C, Gao Y F, Luo K, Zhao Z S, Wang L M, Wen B, He J L, Liu Z Y 2013 Nature 493 385 Google Scholar
[6]	Huang Q, Yu D L, Xu B, Hu W T, Ma Y M, Wang Y B, Zhao Z S, Wen B, He J L, Liu Z Y, Tian Y J 2014 Nature 510 250 Google Scholar
[7]	徐波, 田永君 2017 66 036201 Google Scholar Xu B, Tian Y J 2017 Acta Phys. Sin. 66 036201 Google Scholar
[8]	Kaner R B, Gilman J J, Tolbert S H 2005 Science 308 1268 Google Scholar
[9]	Cumberland R W, Weinberger M B, Gilman J J, Clark S M, Tolbert S H, Kaner R B 2005 J. Am. Chem. Soc. 127 7264 Google Scholar
[10]	Chung H Y, Weinberger M B, Levine J B, Kavner A, Yang J M, Tolbert S H, Kaner R B 2007 Science 316 436 Google Scholar
[11]	Li Q, Zhou D, Zheng W T, Ma Y M, Chen C F 2013 Phys. Rev. Lett. 110 136403 Google Scholar
[12]	Zhao C M, Duan Y F, Gao J, Liu W J, Dong H M, Dong H F, Zhang D K, Oganov A R 2018 Phys. Chem. Chem. Phys. 20 24665 Google Scholar
[13]	Gregoryanz E, Sanloup C, Somayazulu M, Badro J, Fiquet G, Mao H K, Hemley R J 2004 Nat. Mater. 3 294 Google Scholar
[14]	Young A F, Sanloup C, Gregoryanz E, Scandolo S, Hemley R J, Mao H K 2006 Phys. Rev. Lett. 96 155501 Google Scholar
[15]	Ivanovskii A L 2012 Prog. Mater. Sci. 57 184 Google Scholar
[16]	陶强, 马帅领, 崔田, 朱品文 2017 66 036103 Google Scholar Tao Q, Ma S L, Cui T, Zhu P W 2017 Acta Phys. Sin. 66 036103 Google Scholar
[17]	Hillebrecht H, Gebhardt K 2001 Angewandte Chemie (Int. Ed. in English) 40 1445 Google Scholar
[18]	Oganov A R, Glass C W 2006 J. Chem. Phys. 124 244704 Google Scholar
[19]	Wang Y C, Lü J A, Zhu L, Ma Y M 2010 Phys. Rev. B 82 094116 Google Scholar
[20]	Kresse G, Furthmüller J 1996 Phys. Rev. B 54 11169 Google Scholar
[21]	Le Page Y, Saxe P 2002 Phys. Rev. B 65 104104 Google Scholar
[22]	Togo A, Tanaka I 2015 Scr. Mater. 108 1 Google Scholar
[23]	Jain A, Ong S P, Hautier G, Chen W, Richards W D, Dacek S, Cholia S, Gunter D, Skinner D, Ceder G, Persson K A 2013 APL Mater. 1 011002 Google Scholar
[24]	Togo A, Chaput L, Tanaka I, Hug G 2010 Phys. Rev. B 81 174301 Google Scholar
[25]	Mouhat F, Coudert F X 2014 Phys. Rev. B 90 224104 Google Scholar
[26]	Wu Z J, Zhao E J, Xiang H P, Hao X F, Liu X J, Meng J 2007 Phys. Rev. B 76 054115 Google Scholar
[27]	Pugh S F 1954 Philos. Mag. 45 823 Google Scholar
[28]	Chen X Q, Niu H Y, Li D Z, Li Y Y 2011 Intermetallics 19 1275 Google Scholar

Cited By

图 1 (a), (b) Nb₃B₃C和(c), (d) Nb₄B₃C₂的晶体结构(棕球, Nb原子; 蓝球, B原子; 粉球, C原子; Nb₆B三棱柱和Nb₆C八面体分别用绿色和褐色表示)

Figure 1. Crystal structures of the (a), (b) Nb₃B₃C and (c), (d) Nb₄B₃C₂. The light brown, blue and pink spheres represent Nb, B and C atoms, respectively. The Nb₆B trigonal prisms and Nb₆C octahedrons are painted green and dark brown.

DownLoad: Full-Size Img PowerPoint

图 2 不同温度下Ta₃B₃C, Ta₄B₃C₂相分别和其相应最稳定竞争组合相的自由能之差

Figure 2. Energy differences of Ta₃B₃C and Ta₄B₃C₂ phases with respect to their most competing phases as a function of temperature.

DownLoad: Full-Size Img PowerPoint

图 3 (a) Ta₃B₃C和(b) Ta₄B₃C₂结构的声子色散曲线

Figure 3. Phonon dispersion curves of (a) Ta₃B₃C and (b) Ta₄B₃C₂ structures.

DownLoad: Full-Size Img PowerPoint

图 4 (a), (c) Ta₃B₃C和(b), (d) Ta₄B₃C₂结构的能带结构和态密度图

Figure 4. Band structures and density of states of (a), (c) Ta₃B₃C and (b), (d) Ta₄B₃C₂ structures.

DownLoad: Full-Size Img PowerPoint

表 1 Nb₃B₃C, Nb₄B₃C₂, Ta₃B₃C和Ta₄B₃C₂晶体的结构参数

Table 1. Structural parameters of the Nb₃B₃C, Nb₄B₃C₂, Ta₃B₃C and Ta₄B₃C₂ configurations.

模型	晶系和空间群	晶格参数(Å, degree)	原子坐标
Nb₃B₃C	Orthorhombic Cmcm	a = 3.284, 3.265^a, b = 28.877, 28.710^a, c = 3.144, 3.129^a, α = β = γ = 90	Nb1 (4c) (0, 0.2128, 0.25), Nb2 (4c) (0, 0.3620, 0.25), Nb3 (4c) (0, 0.4532, 0.25), B1 (4c) (0, 0.1120, 0.25), B2 (4c) (0, 0.0155, 0.25), B3 (4c) (0, 0.0790, 0.25), C (4c) (0, 0.2878, 0.25)
Nb₄B₃C₂	Orthorhombic Cmcm	a = 3.257, 3.229^a, b = 37.874, 37.544^a, c = 3.153, 3.133^a, α = β = γ = 90	Nb1 (4c) (0, 0.1621, 0.75), Nb2 (4c) (0, 0.2805, 0.75), Nb3 (4c) (0, 0.3946, 0.75), Nb4 (4c) (0, 0.4642, 0.25), B1 (4c) (0, 0.0854, 0.75), B2 (4c) (0, 0.0118, 0.25), B3 (4c) (0, 0.0602, 0.25), C1 (4c) (0, 0.2202, 0.75), C2 (4c) (0, 0.3383, 0.75)
Ta₃B₃C	Orthorhombic Cmcm	a = 3.267, b = 28.688, c = 3.133, α = β = γ = 90	Ta1 (4c) (0, 0.2121, 0.25), Ta2 (4c) (0, 0.3619, 0.25), Ta3 (4c) (0, 0.4531, 0.25), B1 (4c) (0, 0.1130, 0.25), B2 (4c) (0, 0.0155, 0.25), B3 (4c) (0, 0.0791, 0.25), C (4c) (0, 0.2874, 0.25)
Ta₄B₃C₂	Orthorhombic Cmcm	a = 3.243, b = 37.609, c = 3.141, α = β = γ = 90	Ta1 (4c) (0, 0.1615, 0.75), Nb2 (4c) (0, 0.2806, 0.75), Nb3 (4c) (0, 0.3945, 0.75), Nb4 (4c) (0, 0.4641, 0.25), B1 (4c) (0, 0.0861, 0.75), B2 (4c) (0, 0.0118, 0.25), B3 (4c) (0, 0.0602, 0.25), C1 (4c) (0, 0.2202, 0.75), C2 (4c) (0, 0.3380, 0.75)
注: ^a文献[17]中的实验值.

DownLoad: CSV

表 2 不同成分TM₃B₃C和TM₄B₃C₂的形成焓(eV/atom)

Table 2. Calculated formation enthalpies of different TM₃B₃C and TM₄B₃C₂ phases (eV/atom).

TM	TM₃B₃C			TM₄B₃C₂
TM	$\Delta {H_{{\rm{elements}}}}$	$\Delta {H_{{\rm{comp}}}}$	最稳定竞争组合	$\Delta {H_{{\rm{elements}}}}$	$\Delta {H_{{\rm{comp}}}}$	最稳定竞争组合
Sc	–0.637	0.071	6ScB₂ + Sc₄C₃ + Sc₂C = 4Sc₃B₃C	–0.520	0.144	10ScB₂ + 4Sc₄C₃ + Sc₂BC₂ = 7Sc₄B₃C₂
Ti	–0.896	0.019	9TiB₂ + TiC + Ti₈C₅ = 6Ti₃B₃C	–0.863	0.018	9TiB₂ + 7TiC + Ti₈C₅ = 6Ti₄B₃C₂
V	–0.687	0.101	3VB + C = V₃B₃C	–0.628	0.092	18VB + 7C + V₆C₅ = 6V₄B₃C₂
Cr	–0.294	0.159	3CrB + C = Cr₃B₃C	–0.194	0.178	9CrB + 4C + Cr₃C₂ = 3Cr₄B₃C₂
Mn	–0.100	0.195	3MnB + C = Mn₃B₃C	0.024
Fe	0.002			0.139
Co	0.094			0.255
Ni	0.296			0.456
Cu	0.738			0.959
Zn	0.713			0.929
Y	–0.385	0.089	9YB₂ + 5Y₂C + Y₂B₃C₂ = 7Y₃B₃C	–0.283	0.160	6YB₂ + 8Y₂C + 3Y₂B₃C₂ = 7Y₄B₃C₂
Zr	–0.851	0.019	3ZrB₂ + 2ZrC + Zr = 2Zr₃B₃C	–0.838	0.020	3ZrB₂ + 4ZrC + Zr = 2Zr₄B₃C₂
Nb	–0.698	–0.023	3NbB + C = Nb₃B₃C	–0.661	–0.002	C + 6Nb₃B₃C + Nb₆C₅ = 6Nb₄B₃C₂
Mo	–0.257	0.175	3MoB + C = Mo₃B₃C	–0.155	0.202	3MoB + C + MoC = Mo₄B₃C₂
Tc	–0.005	0.326	12TcB₂ + 11C + 3Tc₇B₃ = 11Tc₃B₃C	0.138
Ru	0.211			–0.369
Rh	0.230			–0.406
Pd	0.552			0.744
Ag	1.027			1.295
Cd	0.846			1.112
Hf	–0.920	0.016	3HfB₂ + 2HfC + Hf = 2Hf₃B₃C	–0.922	0.018	3HfB₂ + 4HfC + Hf = 2Hf₄B₃C₂
Ta	–0.704	0.003	3Ta₃B₄ + C + 3TaC = 4Ta₃B₃C	–0.691	–0.010	3Ta₃B₄ + C + 7TaC = 4Ta₄B₃C₂
W	–0.094	0.227	3WB + C = W₃B₃C	–0.007	0.273	3WB + C + WC = W₄B₃C₂
Re	0.281			0.425
Os	0.590			0.755
Ir	0.604			0.758
Pt	0.708			0.855
Au	1.096			1.310
Hg	1.186			1.333

DownLoad: CSV

表 3 Ta₃B₃C, Ta₄B₃C₂结构的弹性常数、体弹模量、剪切模量和维氏硬度 (GPa)

Table 3. Calculated elastic constants C_ij, bulk modulus B, shear modulus G, Vickers hardness H_V of Ta₃B₃C and Ta₄B₃C₂ configurations (GPa).

结构	弹性常数									力学性能^a			硬度
结构	C₁₁	C₂₂	C₃₃	C₄₄	C₅₅	C₆₆	C₁₂	C₁₃	C₂₃	B	G	B/G	H_Chen	H_Tian
Ta₃B₃C	569.6	514.4	563.5	194.1	180.0	261.8	187.1	147.3	173.9	295.9	200.8	1.47	25.3	25.3
Ta₄B₃C₂	581.1	535.3	602.1	197.3	185.1	275.8	200.3	146.0	170.2	305.7	209.0	1.46	26.2	26.2
Nb₃B₃C	544.3	479.8	522.8	181.5	171.9	245.3	170.9	132.9	162.2	275.3	189.7	1.45	24.8	24.7
Nb₄B₃C₂	551.5	499.2	548.5	184.0	175.1	257.1	183.2	132.7	157.8	282.9	195.8	1.44	25.5	25.4
TaB₂										302	200	1.51	24.4	24.5
NbB₂										287	195	1.47	24.8	24.8
TaC										324	215	1.51	25.6	25.9
NbC										239	161	1.48	21.6	21.4
SiC										213	187	1.14	33.6	32.2
Al₂O₃										232	147	1.58	18.7	18.7
TiN										259	180	1.44	24.3	24.0
注: ^a二元相力学性能数据来自Materials Project网站.

DownLoad: CSV

map

[1]	Tian Y J, Xu B, Zhao Z S 2012 Int. J. Refract. Met. Hard Mat. 33 93 Google Scholar
[2]	包括, 马帅领, 徐春红, 崔田 2017 66 036104 Google Scholar Bao K, Ma S L, Xu C H, Cui T 2017 Acta Phys. Sin. 66 036104 Google Scholar
[3]	Zhou X F, Sun J, Fan Y X, Chen J, Wang H T, Guo X J, He J L, Tian Y J 2007 Phys. Rev. B 76 100101 Google Scholar
[4]	Dong H F, Oganov A R, Wang Q G, Wang S N, Wang Z H, Zhang J, Esfahani M M D, Zhou X F, Wu F G, Zhu Q 2016 Sci. Rep. 6 31288 Google Scholar
[5]	Tian Y J, Xu B, Yu D L, Ma Y M, Wang Y B, Jiang Y B, Hu W T, Tang C C, Gao Y F, Luo K, Zhao Z S, Wang L M, Wen B, He J L, Liu Z Y 2013 Nature 493 385 Google Scholar
[6]	Huang Q, Yu D L, Xu B, Hu W T, Ma Y M, Wang Y B, Zhao Z S, Wen B, He J L, Liu Z Y, Tian Y J 2014 Nature 510 250 Google Scholar
[7]	徐波, 田永君 2017 66 036201 Google Scholar Xu B, Tian Y J 2017 Acta Phys. Sin. 66 036201 Google Scholar
[8]	Kaner R B, Gilman J J, Tolbert S H 2005 Science 308 1268 Google Scholar
[9]	Cumberland R W, Weinberger M B, Gilman J J, Clark S M, Tolbert S H, Kaner R B 2005 J. Am. Chem. Soc. 127 7264 Google Scholar
[10]	Chung H Y, Weinberger M B, Levine J B, Kavner A, Yang J M, Tolbert S H, Kaner R B 2007 Science 316 436 Google Scholar
[11]	Li Q, Zhou D, Zheng W T, Ma Y M, Chen C F 2013 Phys. Rev. Lett. 110 136403 Google Scholar
[12]	Zhao C M, Duan Y F, Gao J, Liu W J, Dong H M, Dong H F, Zhang D K, Oganov A R 2018 Phys. Chem. Chem. Phys. 20 24665 Google Scholar
[13]	Gregoryanz E, Sanloup C, Somayazulu M, Badro J, Fiquet G, Mao H K, Hemley R J 2004 Nat. Mater. 3 294 Google Scholar
[14]	Young A F, Sanloup C, Gregoryanz E, Scandolo S, Hemley R J, Mao H K 2006 Phys. Rev. Lett. 96 155501 Google Scholar
[15]	Ivanovskii A L 2012 Prog. Mater. Sci. 57 184 Google Scholar
[16]	陶强, 马帅领, 崔田, 朱品文 2017 66 036103 Google Scholar Tao Q, Ma S L, Cui T, Zhu P W 2017 Acta Phys. Sin. 66 036103 Google Scholar
[17]	Hillebrecht H, Gebhardt K 2001 Angewandte Chemie (Int. Ed. in English) 40 1445 Google Scholar
[18]	Oganov A R, Glass C W 2006 J. Chem. Phys. 124 244704 Google Scholar
[19]	Wang Y C, Lü J A, Zhu L, Ma Y M 2010 Phys. Rev. B 82 094116 Google Scholar
[20]	Kresse G, Furthmüller J 1996 Phys. Rev. B 54 11169 Google Scholar
[21]	Le Page Y, Saxe P 2002 Phys. Rev. B 65 104104 Google Scholar
[22]	Togo A, Tanaka I 2015 Scr. Mater. 108 1 Google Scholar
[23]	Jain A, Ong S P, Hautier G, Chen W, Richards W D, Dacek S, Cholia S, Gunter D, Skinner D, Ceder G, Persson K A 2013 APL Mater. 1 011002 Google Scholar
[24]	Togo A, Chaput L, Tanaka I, Hug G 2010 Phys. Rev. B 81 174301 Google Scholar
[25]	Mouhat F, Coudert F X 2014 Phys. Rev. B 90 224104 Google Scholar
[26]	Wu Z J, Zhao E J, Xiang H P, Hao X F, Liu X J, Meng J 2007 Phys. Rev. B 76 054115 Google Scholar
[27]	Pugh S F 1954 Philos. Mag. 45 823 Google Scholar
[28]	Chen X Q, Niu H Y, Li D Z, Li Y Y 2011 Intermetallics 19 1275 Google Scholar

[1]	Wang Jing, Gao Shan, Duan Xiang-Mei, Yin Wan-Jian. Influence of defect in perovskite solar cell materials on device performance and stability. Acta Physica Sinica, 2024, 73(6): 063101. doi: 10.7498/aps.73.20231631
[2]	Zhang Qiao, Tan Wei, Ning Yong-Qi, Nie Guo-Zheng, Cai Meng-qiu, Wang Jun-Nian, Zhu Hui-Ping, Zhao Yu-Qing. Prediction of Magnetic Janus Materials Based on Machine Learning and First-Principles Calculations. Acta Physica Sinica, 2024, 73(23): 230201. doi: 10.7498/aps.73.20241278
[3]	Song Rui, Liu Xue-Mei, Wang Hai-Bin, Lü Hao, Song Xiao-Yan. Hardness prediction of WC-Co cemented carbide based on machine learning model. Acta Physica Sinica, 2024, 73(12): 126201. doi: 10.7498/aps.73.20240284
[4]	Zhou Jin-Ping, Li Chun-Mei, Jiang Bo, Huang Ren-Zhong. First-principles study of Co and Ni excess effects on crystal structure and phase stability of Co₂NiGa alloy. Acta Physica Sinica, 2023, 72(15): 156301. doi: 10.7498/aps.72.20230626
[5]	Yao Yi-Zhou, Cao Dan, Yan Jie, Liu Xue-Yin, Wang Jian-Feng, Jiang Zhou-Ting, Shu Hai-Bo. A first-principles study on environmental stability and optoelectronic properties of bismuth oxychloride/ cesium lead chloride van der Waals heterojunctions. Acta Physica Sinica, 2022, 71(19): 197901. doi: 10.7498/aps.71.20220544
[6]	Liu Zi-Yuan, Pan Jin-Bo, Zhang Yu-Yang, Du Shi-Xuan. First principles calculation of two-dimensional materials at an atomic scale. Acta Physica Sinica, 2021, 70(2): 027301. doi: 10.7498/aps.70.20201636
[7]	Wang Yan, Chen Nan-Di, Yang Chen, Zeng Zhao-Yi, Hu Cui-E, Chen Xiang-Rong. Thermoelectric transport properties of two-dimensional materials XTe₂ (X = Pd, Pt) via first-principles calculations. Acta Physica Sinica, 2021, 70(11): 116301. doi: 10.7498/aps.70.20201939
[8]	Hu Qian-Ku, Qin Shuang-Hong, Wu Qing-Hua, Li Dan-Dan, Zhang Bin, Yuan Wen-Feng, Wang Li-Bo, Zhou Ai-Guo. First-principles calculations of stabilities and physical properties of ternary niobium borocarbides and tantalum borocarbides. Acta Physica Sinica, 2020, 69(11): 116201. doi: 10.7498/aps.69.20200234
[9]	Zheng Lu-Min, Zhong Shu-Ying, Xu Bo, Ouyang Chu-Ying. First-principles study of rare-earth-doped cathode materials Li₂MnO₃ in Li-ion batteries. Acta Physica Sinica, 2019, 68(13): 138201. doi: 10.7498/aps.68.20190509
[10]	Wang Dan, Zou Juan, Tang Li-Ming. Stability and electronic structure of hydrogenated two-dimensional transition metal dichalcogenides: First-principles study. Acta Physica Sinica, 2019, 68(3): 037102. doi: 10.7498/aps.68.20181597
[11]	Huang Bing-Quan, Zhou Tie-Ge, Wu Dao-Xiong, Zhang Zhao-Fu, Li Bai-Kui. Properties of vacancies and N-doping in monolayer g-ZnO: First-principles calculation and molecular orbital theory analysis. Acta Physica Sinica, 2019, 68(24): 246301. doi: 10.7498/aps.68.20191258
[12]	Chen Xian, Cheng Mei-Juan, Wu Shun-Qing, Zhu Zi-Zhong. First-principle study of structure stability and electronic structures of graphyne derivatives. Acta Physica Sinica, 2017, 66(10): 107102. doi: 10.7498/aps.66.107102
[13]	Bai Jing, Wang Xiao-Shu, Zu Qi-Rui, Zhao Xiang, Zuo Liang. Defect stabilities and magnetic properties of Ni-X-In (X= Mn, Fe and Co) alloys: a first-principle study. Acta Physica Sinica, 2016, 65(9): 096103. doi: 10.7498/aps.65.096103
[14]	Chen Hai-Jun, Li Gao-Qing, Xue Ju-Kui. Variational-method analysis of stability of Bose-Fermi mixture. Acta Physica Sinica, 2011, 60(4): 040304. doi: 10.7498/aps.60.040304.1
[15]	Qu Nian-Rui, Gao Fa-Ming. Theoretical study on electronic structure and properties of solid carbon dioxide. Acta Physica Sinica, 2011, 60(6): 067102. doi: 10.7498/aps.60.067102
[16]	Wang Zhi-Gang, Zhang Yang, Wen Yu-Hua, Zhu Zi-Zhong. First-principles calculation of structural stability and electronic properties of ZnO atomic chains. Acta Physica Sinica, 2010, 59(3): 2051-2056. doi: 10.7498/aps.59.2051
[17]	Wang Zuo-Lei. Stability and Hopf bifurcation of the simplified Lang-Kobayashi equation. Acta Physica Sinica, 2008, 57(8): 4771-4776. doi: 10.7498/aps.57.4771
[18]	Song Qing-Gong, Jiang En-Yong, Pei Hai-Lin, Kang Jian-Hai, Guo Ying. First principles computational study on the stability of Li ion-vacancy two-dimensional ordered structures in intercalation compounds LixTiS2. Acta Physica Sinica, 2007, 56(8): 4817-4822. doi: 10.7498/aps.56.4817
[19]	Wang Yan, Han Xiao-Yan, Ren Hui-Zhi, Hou Guo-Fu, Guo Qun-Chao, Zhu Feng, Zhang De-Kun, Sun Jian, Xue Jun-Ming, Zhao Ying, Geng Xin-Hua. Stability of mixed phase silicon thin film material under light soaking. Acta Physica Sinica, 2006, 55(2): 947-951. doi: 10.7498/aps.55.947
[20]	Zhang Kai, Feng Jun. Symmetry and stability of a relativistic birkhoff system. Acta Physica Sinica, 2005, 54(7): 2985-2989. doi: 10.7498/aps.54.2985

Catalog

Vol. 68, Issue 9 - 2019-05-05

Metrics

Abstract views: 10037
PDF Downloads: 113
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板

Theoretical calculations of stabilities and properties of transition metal borocarbides TM₃B₃C and TM₄B₃C₂ compound

Abstract

Authors and contacts

Corresponding author: Hu Qian-Ku, hqk@hpu.edu.cn

FullText HTML : translate this paragraph

References

Cited By

Catalog

Metrics

Authors

Referees

About Journal

About

Search

Article

留言板