-
采用基于密度泛函理论的第一性原理计算方法, 系统地研究了带缺陷的二维类石墨烯结构的ZnO (graphene like-ZnO, g-ZnO)的几何结构、电子结构、磁性性质和吸收光谱性质. 研究的缺陷类型包括锌原子空位(VZn_g-ZnO)、氧原子空位(VO_g-ZnO)、氮原子取代氧原子(NO_g-ZnO)和表面吸附氮原子(N@g-ZnO). 研究发现: NO_g-ZnO体系和N@g-ZnO体系形变较小, 而空位体系会引入较大的形变; g-ZnO本身无磁矩, 引入Zn空位后, VZn_g-ZnO体系总磁矩为2.00 μB; VO_g-ZnO体系无磁矩, 但N掺杂后的NO_g-ZnO体系和氮吸附的N@g-ZnO体系的总磁矩分别为1.00 μB和3.00 μB. 利用掺杂体系的局域对称性和分子轨道理论分析了杂质能级和磁矩的产生原因, 并且通过分析光吸收曲线得知, 引入空位缺陷或者N原子掺杂, 可以有效增强g-ZnO单层材料的光吸收性能. 研究结果对系统地理解g-ZnO及其缺陷模型的性质有重要意义, 可以为发展基于g-ZnO的纳米电子器件和光催化应用提供理论参考.The geometric structure, electronic structure, magnetic properties and absorption spectrum of graphene-like ZnO (g-ZnO) monolayer supercell with defects are systemically studied by the first-principles calculation based on density functional theory in this work. The defect supercell model includes zinc atom vacancy (VZn_g-ZnO), oxygen atom vacancy (VO_g-ZnO), nitrogen atom substituted for oxygen atom (NO_g-ZnO) and nitrogen adsorbed on the g-ZnO monolayer (N@g-ZnO). The results indicate that the geometric deformation induced by N-doping in NO_g-ZnO and N@g-ZnO structure is negligible, while that of supercell with vacancy is relatively large. The O atoms neighboring a Zn vacancy center in VZn_g-ZnO model move away from each other as a result of symmetry breaking. As a contrast, three N atoms around VO center move into VZn_g-ZnO supercell. The pristine g-ZnO is non-magnetic. But the magnetic moment of VZn_g-ZnO is 2.00 μB in total as a result of symmetry breaking. The partial magnetic moment mainly results from the p-orbitals of the three neighboring O atoms. VO_g-ZnO has no magnetic moment, but possesses the electronic structure with identical spin-up and spin-down. The total magnetic moment of the N-doped NO_g-ZnO is 1.00 μB, and the total magnetic moment of N@g-ZnO is 3.00 μB. Their local magnetic moments are mainly contributed by the p-orbitals of N atom. The density of states and the spin density are given to analyze the magnetic properties. Based on the supercell local symmetry and molecular orbital theory, the origin of magnetic moment is well explained. The magnetic VZn_g-ZnO, NO_g-ZnO and N@g-ZnO supercell are found to have a D3h, D3h and C3v local symmetry, respectively, which well explains that their total magnetic moments are 2.00 μB, 1.00 μB and 3.00 μB, respectively. The optical absorption characteristics are also discussed. An enhancement of light absorption can be observed for the defective supercells, due to the introduction of defect states into the band gap. The optical transition between gap state and valance band leads to the below band gap absorption. These results are of insightful guidance for understanding properties of graphene-like ZnO monolayer as well as g-ZnO with vacancy and N dopant, and can be theoretically adopted for investigating the nano-electronic devices and catalytic applications based on g-ZnO monolayer.
-
Keywords:
- two-dimensional material /
- ZnO /
- defect /
- molecular orbital theory /
- first-principles calculation
[1] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666
Google Scholar
[2] Zhang Y, Tan Y, Stormer H L, Kim P 2005 Nature 438 201
Google Scholar
[3] Kerelsky A, Mcgilly L J, Kennes D M, Xian L, Yankowitz M, Chen S, Watanabe K, Taniguchi T, Hone J, Dean C, Rubio A, Pasupathy A N 2019 Nature 572 95
Google Scholar
[4] Ta H, Zhao L, Pohl D, Pang J, Trzebicka B, Rellinghaus B, Pribat D, Gemming T, Liu Z, Bachmatiuk A, Rümmeli M 2016 Crystals 6 100
Google Scholar
[5] Weng Q, Wang X, Wang X, Bando Y, Golberg D 2016 Chem. Soc. Rev. 45 3989
Google Scholar
[6] Zhang Z, Geng Z, Cai D, Pan T, Chen Y, Dong L, Zhou T 2015 Physica E 65 24
Google Scholar
[7] Wang Q H, Kalantar-Zadeh K, Kis A, Coleman J N, Strano M S 2012 Nat. Nanotechnol. 7 699
Google Scholar
[8] Gao Z, Zhou Z, Tománek D 2019 ACS Nano 13 5103
Google Scholar
[9] Ye M, Seo H, Galli G 2019 npj Comput. Mater. 5 44
Google Scholar
[10] Zhu C, Gao D, Ding J W, Chao D, Wang J 2018 Chem. Soc. Rev. 47 4332
Google Scholar
[11] Liu Y, Huang Y, Duan X 2019 Nature 567 323
Google Scholar
[12] Claeyssens F, Freeman C L, Allan N L, Sun Y, Ashfold M N R, Harding J H 2005 J. Mater. Chem. 15 139
Google Scholar
[13] Tusche C, Meyerheim H L, Kirschner J 2007 Phys. Rev. Lett. 99 26102
Google Scholar
[14] Topsakal M, Cahangirov S, Bekaroglu E, Ciraci S 2009 Phys. Rev. B 80 235119
Google Scholar
[15] Zheng F B, Zhang C W, Wang P J, Luan H X 2012 J. Appl. Phys. 111 44329
Google Scholar
[16] Peng Q, Liang C, Ji W, De S 2013 Comp. Mater. Sci. 68 320
Google Scholar
[17] Guo H, Zhao Y, Lu N, Kan E, Zeng X C, Wu X, Yang J 2012 J. Phys. Chem. C 116 11336
Google Scholar
[18] Chen J L, Devi N, Li N, Fu D J, Ke X W 2018 Chin. Phys. B 27 086102
Google Scholar
[19] Tan J T, Zhang S F, Qian M C, Luo H J, Wu F, Long X M, Fang L, Wei D P, Hu B S 2018 Chin. Phys. B 27 114401
Google Scholar
[20] Zheng S W, Fan G H, He M, Zhang T 2014 Chin. Phys. B 23 066301
Google Scholar
[21] 侯清玉, 曲灵丰, 赵春旺 2016 65 057401
Google Scholar
Hou Q Y, Qu L F, Zhao C W 2016 Acta Phys. Sin. 65 057401
Google Scholar
[22] 侯清玉, 李勇, 赵春旺 2017 66 067202
Google Scholar
Hou Q Y, Li Y, Zhao C 2017 Acta Phys. Sin. 66 067202
Google Scholar
[23] 张梅玲, 陈玉红, 张材荣, 李公平 2019 68 087101
Google Scholar
Zhang M L, Chen Y H, Zhang C R, Li G P 2019 Acta Phys. Sin. 68 087101
Google Scholar
[24] 张丽丽, 夏桐, 刘桂安, 雷博程, 赵旭才, 王少霞, 黄以能 2019 68 017401
Google Scholar
Zhang L L, Xia T, Liu G A, Lei B C, Zhao X C, Wang S X, Huang Y N 2019 Acta P hys. Sin. 68 017401
Google Scholar
[25] Sun M, Ren Q, Zhao Y, Chou J, Yu J, Tang W 2017 Carbon 120 265
Google Scholar
[26] 张召富, 周铁戈, 左旭 2013 62 083102
Google Scholar
Zhang Z F, Zhou T G, Zuo X 2013 Acta Phys. Sin. 62 083102
Google Scholar
[27] 张召富, 耿朝晖, 王鹏, 胡耀乔, 郑宇斐, 周铁戈 2013 62 246301
Google Scholar
Zhang Z F, Geng Z H, Wang P, Hu Y Q, Zheng Y F, Zhou T G 2013 Acta Phys. Sin. 62 246301
Google Scholar
[28] Zhang Z F, Zhou T G, Zhao H Y, Wei X L 2014 Chin. Phys. B 23 016801
Google Scholar
[29] Hohenberg P, Kohn W 1964 Phys. Rev. 136 864
Google Scholar
[30] Kresse G, Furthmüller J 1996 Phys. Rev. B 54 11169
Google Scholar
[31] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[32] Heyd J, Scuseria G E, Ernzerhof M 2003 J. Chem. Phys. 118 8207
Google Scholar
[33] Blochl P E 1994 Phys. Rev. B 50 17953
Google Scholar
[34] Wang V, Xu N, Liu J, Tang G, Geng W 2019 arXiv: 1908.08269 [cond-mat.mtrl-sci]
[35] Cui J, Liang S, Sun S, Zheng X, Zhang J 2018 J. Phys.: Condens. Matter 30 175001
Google Scholar
[36] Wang S, Ren C, Tian H, Yu J, Sun M 2018 Phys. Chem. Chem. Phys. 20 13394
Google Scholar
[37] Niu X, Li Y, Shu H, Yao X, Wang J 2017 J. Phys. Chem. C 121 3648
Google Scholar
[38] Liu Y, Liu H, Zhou H, Li T, Zhang L 2019 Appl. Surf. Sci. 466 133
Google Scholar
[39] Tu Z C 2010 J. Comput. Theor. Nanosci. 7 1182
-
图 1 理想g-ZnO的(a)晶体结构以及(b)能带和态密度, 其中g-ZnO价带顶对齐到0 eV
Fig. 1. (a) Atomic structures, (b) band structure and density of states (DOS) of the g-ZnO primitive unit cell. The valence band maximum of g-ZnO is referred to 0 eV.
图 2 空位及掺杂超胞体系的几何结构示意图 (a) VZn_g-ZnO; (b) VO_g-ZnO; (c) NO_g-ZnO; (d) N原子吸附在六元环中心上方; (e) N原子吸附在Zn原子上方; (f) N原子吸附在O原子上方
Fig. 2. Atomic structures of the g-ZnO supercells: (a) Ideal g-ZnO; (b) VO_g-ZnO; (c) NO_g-ZnO; (d) N atom at hollow site; (e) N atom on top of Zn atom; (f) N atom on top of O atom.
图 3 总态密度和分波态密度 (a) VZn_g-ZnO; (b) VO_g-ZnO; (c) NO_g-ZnO; (d) N@g-ZnO; 其中g-ZnO的价带顶对齐到0 eV
Fig. 3. Total density of states and partial density of states: (a) VZn_g-ZnO; (b) VO_g-ZnO; (c) NO_g-ZnO; (d) N@g-ZnO. The valence band maximum of g-ZnO is referred to 0 eV.
图 4 能带结构 (a) VZn_g-ZnO; (b) VO_g-ZnO; (c) NO_g-ZnO; (d) N@g-ZnO; 其中g-ZnO的价带顶对齐到0 eV
Fig. 4. Band structure of (a) VZn_g-ZnO; (b) VO_g-ZnO; (c) NO_g-ZnO; (d) N@g-ZnO. The valence band maximum of g-ZnO is referred to 0 eV.
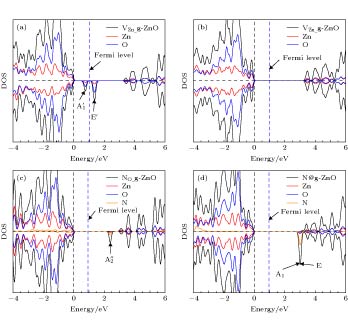
图 5 分子轨道 (a) VZn_g-ZnO体系, O能级劈裂及电子填充示意图; (b) NO_g-ZnO体系, p轨道分裂及电子填充示意图; (c) N@g-ZnO体系, p轨道分裂及电子填充示意图
Fig. 5. Molecular orbital diagrams: (a) VZn_g-ZnO supercell, O energy level splitting and electron filling; (b) NO_g-ZnO supercell, p-orbital splitting and electron filling; (c) N@g-ZnO supercell, p-orbital splitting and electron filling.
图 6 自旋密度图, 其中青色区域是自旋向上, 黄色区域是自旋向下 (a) VZn_g-ZnO体系的自旋密度; (b) VO_g-ZnO体系的自旋密度; (c) NO_g-ZnO体系的自旋密度; (d) N@g-ZnO体系的自旋密度
Fig. 6. Spin density of (a) VZn_g-ZnO, (b) VO_g-ZnO, (c) NO_g-ZnO, and (d) N@g-ZnO supercells, respectively. Cyan is spin up and yellow is spin down.
图 7 理想g-ZnO及具有空位、掺杂的超胞体系的光学吸收谱
Fig. 7. Optical absorption spectra of ideal g-ZnO and the defective supercell systems.
表 1 N掺杂g-ZnO单层的结构参数和结合能
Table 1. Structure parameters and binding energy of N-doped g-ZnO monolayer.
超胞模型 hN/Å hZn/Å hO/Å dZn_N/Å dO_N/Å Eb/eV NO_g-ZnO 0.07 0.005 0.003 1.92 3.31 –4.12 N@g-ZnO 2.12 0.003 –0.104 2.84 2.93 –0.25 
下载: 导出CSV
表 2 N掺杂g-ZnO单层的磁矩
Table 2. Magnetic moment of N-doped g-ZnO monolayer.
超胞模型 Mtot/µB MN/µB MZn/µB MO/µB VO_g-ZnO 0 — 0 0 VZn_g-ZnO 2.00 — 0.02 0.45 NO_g-ZnO 1.00 0.59 0.01 0 N@g-ZnO 3.00 1.90 0 0.05
下载: 导出CSV
-
[1] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666
Google Scholar
[2] Zhang Y, Tan Y, Stormer H L, Kim P 2005 Nature 438 201
Google Scholar
[3] Kerelsky A, Mcgilly L J, Kennes D M, Xian L, Yankowitz M, Chen S, Watanabe K, Taniguchi T, Hone J, Dean C, Rubio A, Pasupathy A N 2019 Nature 572 95
Google Scholar
[4] Ta H, Zhao L, Pohl D, Pang J, Trzebicka B, Rellinghaus B, Pribat D, Gemming T, Liu Z, Bachmatiuk A, Rümmeli M 2016 Crystals 6 100
Google Scholar
[5] Weng Q, Wang X, Wang X, Bando Y, Golberg D 2016 Chem. Soc. Rev. 45 3989
Google Scholar
[6] Zhang Z, Geng Z, Cai D, Pan T, Chen Y, Dong L, Zhou T 2015 Physica E 65 24
Google Scholar
[7] Wang Q H, Kalantar-Zadeh K, Kis A, Coleman J N, Strano M S 2012 Nat. Nanotechnol. 7 699
Google Scholar
[8] Gao Z, Zhou Z, Tománek D 2019 ACS Nano 13 5103
Google Scholar
[9] Ye M, Seo H, Galli G 2019 npj Comput. Mater. 5 44
Google Scholar
[10] Zhu C, Gao D, Ding J W, Chao D, Wang J 2018 Chem. Soc. Rev. 47 4332
Google Scholar
[11] Liu Y, Huang Y, Duan X 2019 Nature 567 323
Google Scholar
[12] Claeyssens F, Freeman C L, Allan N L, Sun Y, Ashfold M N R, Harding J H 2005 J. Mater. Chem. 15 139
Google Scholar
[13] Tusche C, Meyerheim H L, Kirschner J 2007 Phys. Rev. Lett. 99 26102
Google Scholar
[14] Topsakal M, Cahangirov S, Bekaroglu E, Ciraci S 2009 Phys. Rev. B 80 235119
Google Scholar
[15] Zheng F B, Zhang C W, Wang P J, Luan H X 2012 J. Appl. Phys. 111 44329
Google Scholar
[16] Peng Q, Liang C, Ji W, De S 2013 Comp. Mater. Sci. 68 320
Google Scholar
[17] Guo H, Zhao Y, Lu N, Kan E, Zeng X C, Wu X, Yang J 2012 J. Phys. Chem. C 116 11336
Google Scholar
[18] Chen J L, Devi N, Li N, Fu D J, Ke X W 2018 Chin. Phys. B 27 086102
Google Scholar
[19] Tan J T, Zhang S F, Qian M C, Luo H J, Wu F, Long X M, Fang L, Wei D P, Hu B S 2018 Chin. Phys. B 27 114401
Google Scholar
[20] Zheng S W, Fan G H, He M, Zhang T 2014 Chin. Phys. B 23 066301
Google Scholar
[21] 侯清玉, 曲灵丰, 赵春旺 2016 65 057401
Google Scholar
Hou Q Y, Qu L F, Zhao C W 2016 Acta Phys. Sin. 65 057401
Google Scholar
[22] 侯清玉, 李勇, 赵春旺 2017 66 067202
Google Scholar
Hou Q Y, Li Y, Zhao C 2017 Acta Phys. Sin. 66 067202
Google Scholar
[23] 张梅玲, 陈玉红, 张材荣, 李公平 2019 68 087101
Google Scholar
Zhang M L, Chen Y H, Zhang C R, Li G P 2019 Acta Phys. Sin. 68 087101
Google Scholar
[24] 张丽丽, 夏桐, 刘桂安, 雷博程, 赵旭才, 王少霞, 黄以能 2019 68 017401
Google Scholar
Zhang L L, Xia T, Liu G A, Lei B C, Zhao X C, Wang S X, Huang Y N 2019 Acta P hys. Sin. 68 017401
Google Scholar
[25] Sun M, Ren Q, Zhao Y, Chou J, Yu J, Tang W 2017 Carbon 120 265
Google Scholar
[26] 张召富, 周铁戈, 左旭 2013 62 083102
Google Scholar
Zhang Z F, Zhou T G, Zuo X 2013 Acta Phys. Sin. 62 083102
Google Scholar
[27] 张召富, 耿朝晖, 王鹏, 胡耀乔, 郑宇斐, 周铁戈 2013 62 246301
Google Scholar
Zhang Z F, Geng Z H, Wang P, Hu Y Q, Zheng Y F, Zhou T G 2013 Acta Phys. Sin. 62 246301
Google Scholar
[28] Zhang Z F, Zhou T G, Zhao H Y, Wei X L 2014 Chin. Phys. B 23 016801
Google Scholar
[29] Hohenberg P, Kohn W 1964 Phys. Rev. 136 864
Google Scholar
[30] Kresse G, Furthmüller J 1996 Phys. Rev. B 54 11169
Google Scholar
[31] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[32] Heyd J, Scuseria G E, Ernzerhof M 2003 J. Chem. Phys. 118 8207
Google Scholar
[33] Blochl P E 1994 Phys. Rev. B 50 17953
Google Scholar
[34] Wang V, Xu N, Liu J, Tang G, Geng W 2019 arXiv: 1908.08269 [cond-mat.mtrl-sci]
[35] Cui J, Liang S, Sun S, Zheng X, Zhang J 2018 J. Phys.: Condens. Matter 30 175001
Google Scholar
[36] Wang S, Ren C, Tian H, Yu J, Sun M 2018 Phys. Chem. Chem. Phys. 20 13394
Google Scholar
[37] Niu X, Li Y, Shu H, Yao X, Wang J 2017 J. Phys. Chem. C 121 3648
Google Scholar
[38] Liu Y, Liu H, Zhou H, Li T, Zhang L 2019 Appl. Surf. Sci. 466 133
Google Scholar
[39] Tu Z C 2010 J. Comput. Theor. Nanosci. 7 1182
下载:
计量
- 文章访问数: 12963
- PDF下载量: 364
- 被引次数: 0
