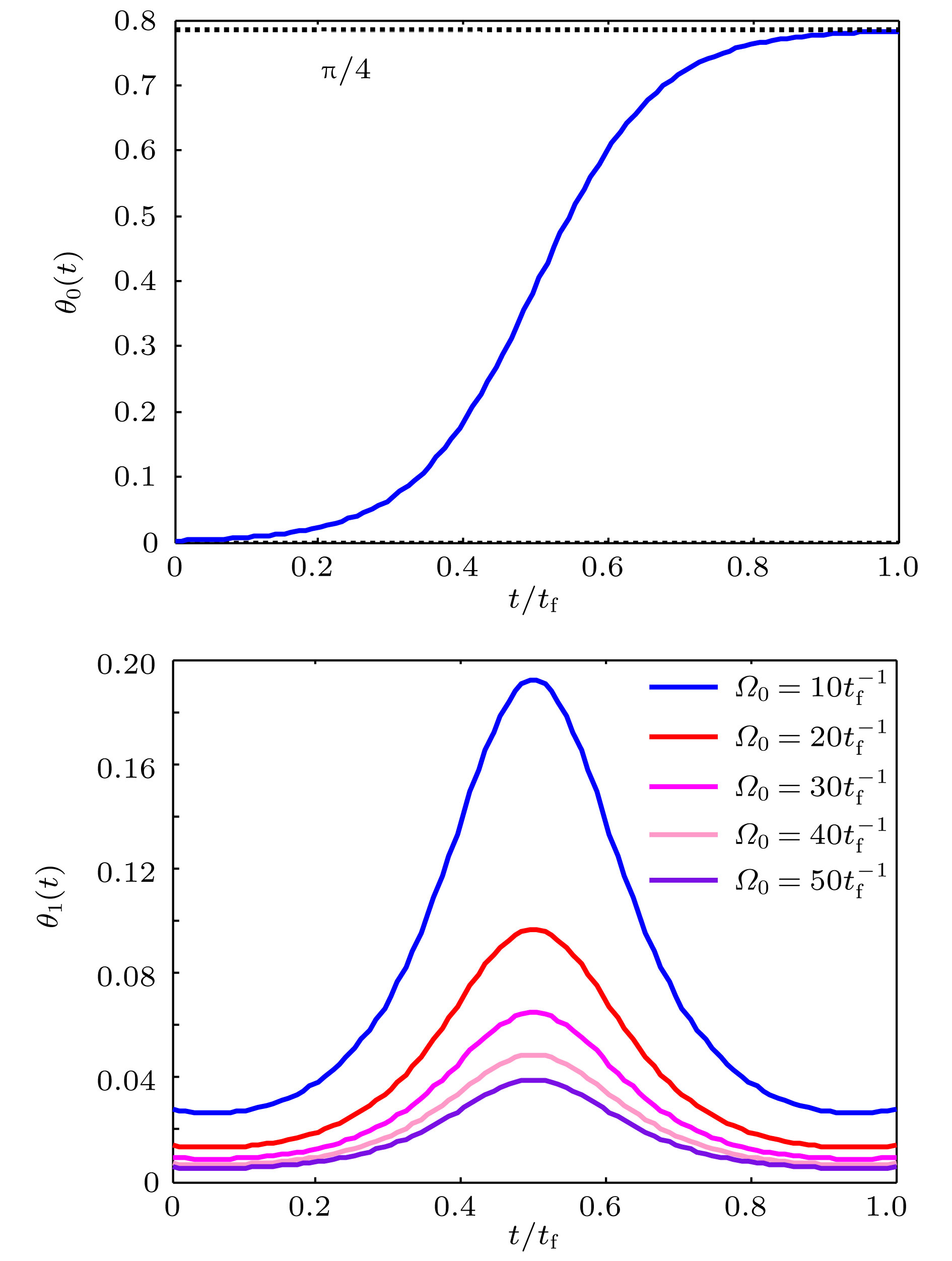
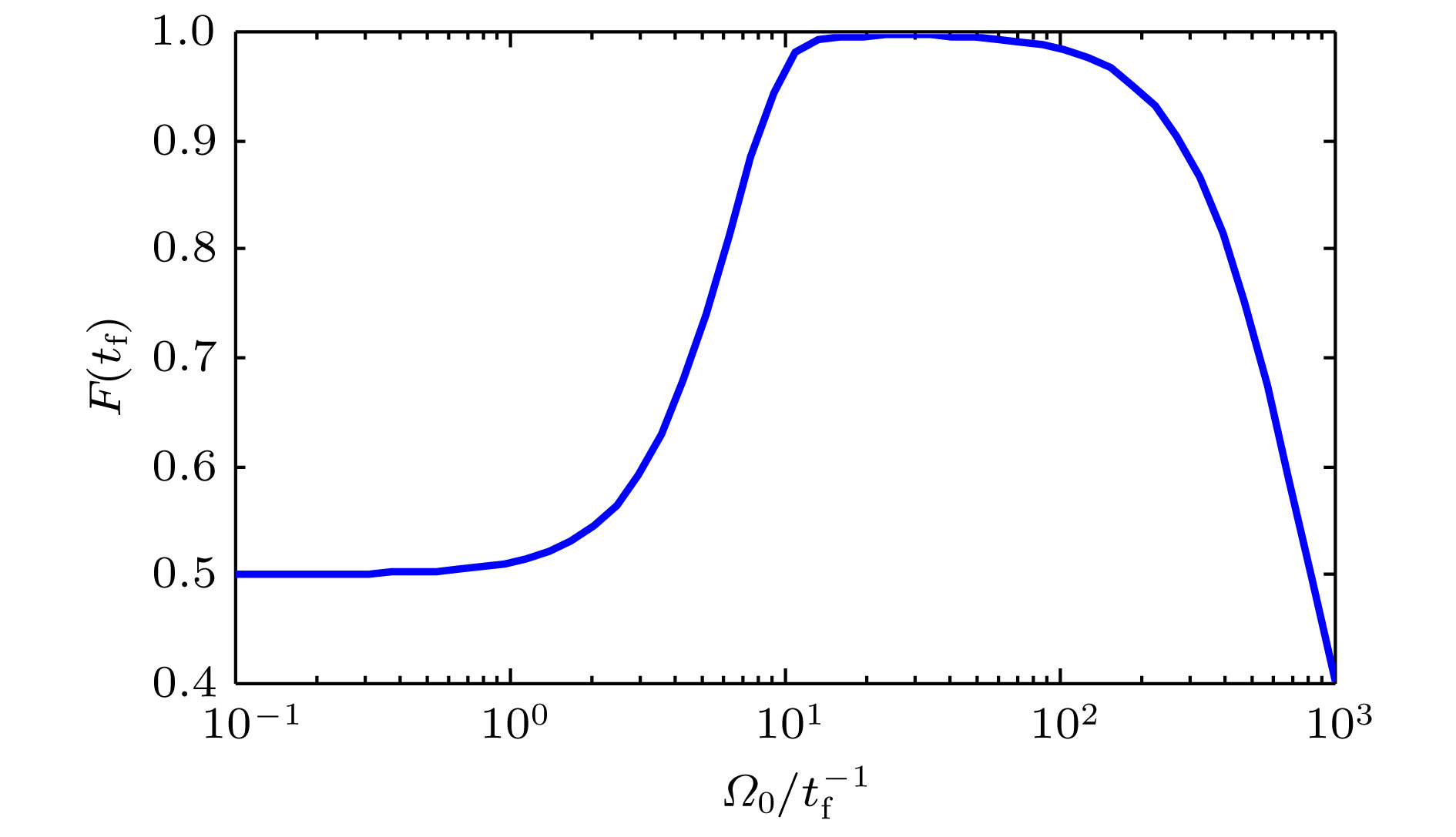
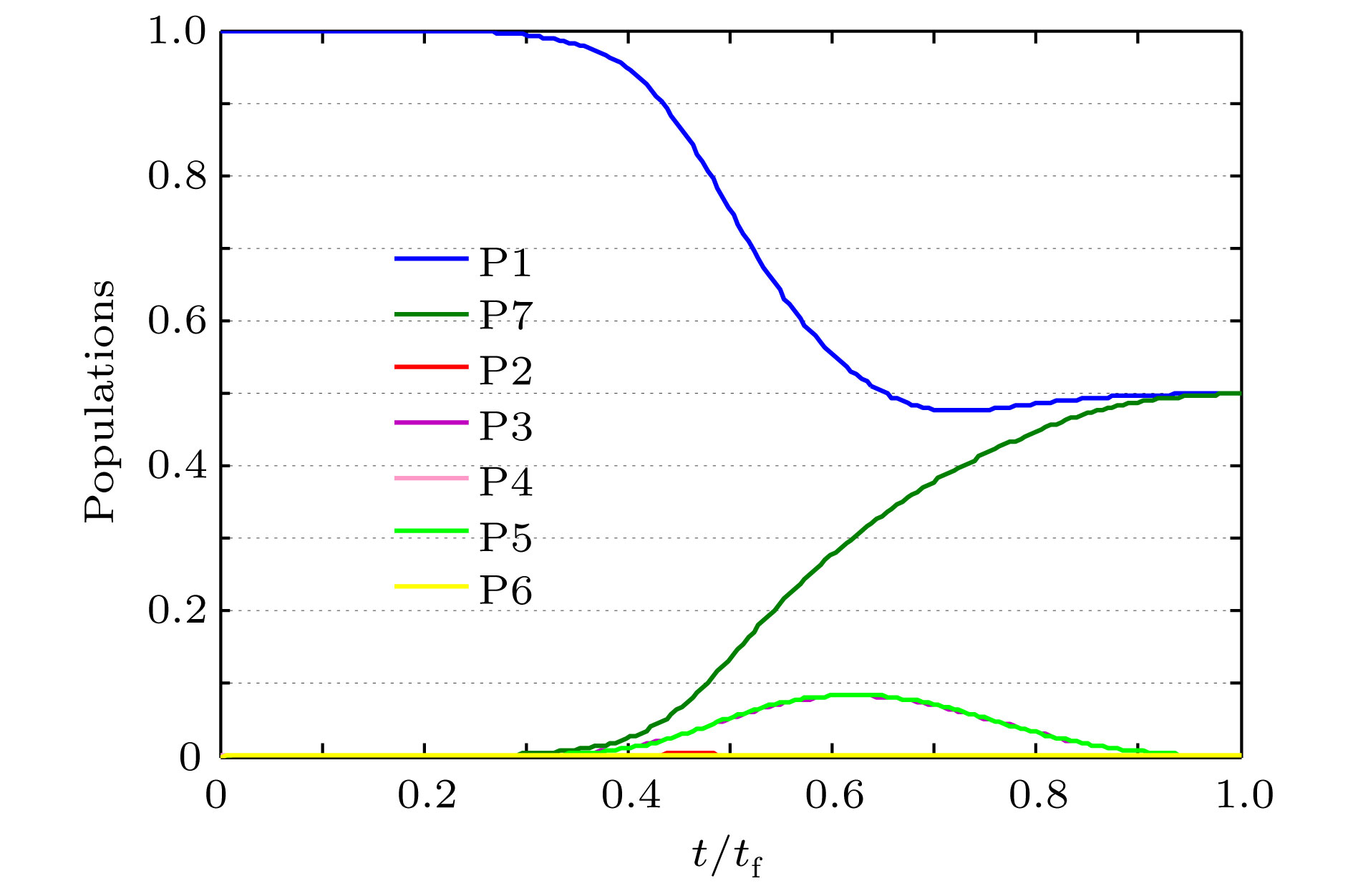
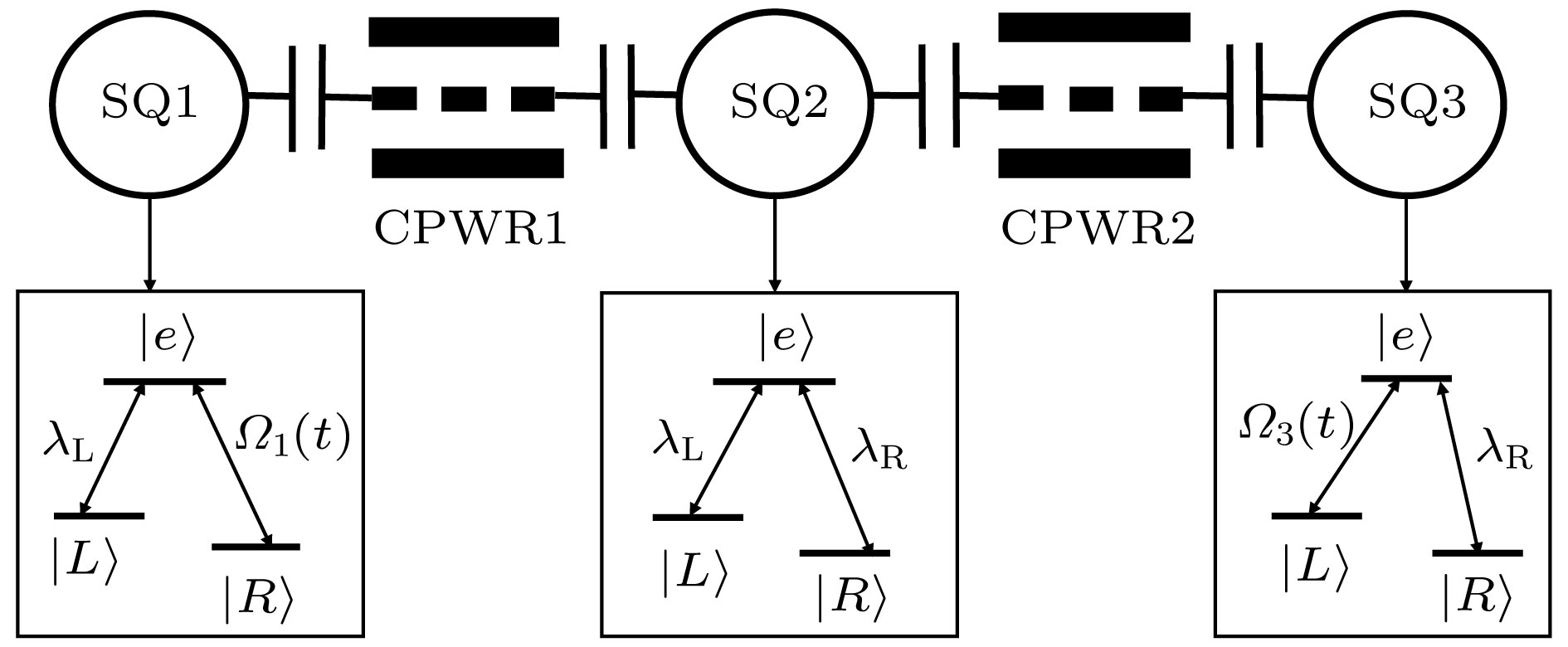
-
With the development of quantum information processing (QIP), entangled states have been used in many important fields. One of the well-known entangled states is Greenberger-Horne-Zeilinger (GHZ) state, which provides a possibility for testing quantum mechanics against local hidden theory without using Bell’s inequality. Many schemes of generating the GHZ state have been put forward in various physical systems over the past ten years. Among these physical systems, the superconducting qubits (SQs) have the potential suitability for the integrated devices in QIP and can be controlled easily through modulating electromagnetic signals and designing level configurations. On the other hand, adiabatic passage is a typical method which is used widely to generate entanglements. However, adiabatic passage needs long evolution time to satisfy the adiabatic condition. Therefore, to speed up a slow quantum adiabatic process, a new kind of technique called " shortcuts to adiabatic passage (STAP)” has attracted much attention. The Lewis-Riesenfeld invariants and transitionless quantum driving are famous methods of STAP. But they are difficult to use in the experiment. For the Lewis-Riesenfeld invariants, the driving pulses are not smoothly turned on or off and thus lead to severe impediments in experiment. For transitionless quantum driving, a direct coupling between the initial state and the target state is needed, but is too hard to obtain experimentally. In this paper, we propose a theoretical scheme for fast generating GHZ state of three superconducting qubits via superadiabatic-based shortcuts. Firstly, with the help of quantum Zeno dynamics, we obtain the effective Hamiltonian of the system, then we choose a suitable counterdiabatic Hamiltonian in the same form as the effective Hamiltonian and add it to the effective Hamiltonian in order to construct shortcuts to adiabatic passage, which can make the system evolve along one of the superadiabatic states and thus accelerate the evolution process of the system. More importantly, the superadiabatic scheme does not need an additional coupling between the initial and finial state, which ensures its high experimental feasibility. In addition, numerical simulation results show that the proposed scheme is robust against spontaneous emission, the cavity photon leakage and the dephasing of SQs.
-
Keywords:
- superadiabatic-based shortcuts /
- superconducting qubit /
- Greenberger-Horne-Zeilinger state
[1] Li X H, Deng F G, Zhou H Y 2006 Phys. Rev. A 74 054302
Google Scholar
[2] Karlsson A, Bourennane M 1998 Phys. Rev. A 58 4394
Google Scholar
[3] Xiao L, Long G L, Deng F G, Pan J W 2004 Phys. Rev. A 69 052307
Google Scholar
[4] Zeilinger A, Horne M A, Weinfurter H 1997 Phys. Rev. Lett. 78 3031
Google Scholar
[5] Zheng S B 2001 Phys. Rev. Lett. 87 230404
Google Scholar
[6] Leibfriend D, Knill E, Seidelin S 2005 Nature 438 639
Google Scholar
[7] Su X L, Tan A, Jia X J 2007 Phys. Rev. Lett. 98 070502
Google Scholar
[8] Raimond J M, Brune M, Haroche S 2001 Rev. Mod. Phys. 73 565
Google Scholar
[9] Kang Y H, Chen Y H, Wu Q C 2016 Sci. Rep. 6 36737
Google Scholar
[10] Clarke J, Wilhelm F K 2008 Nature 453 1031
Google Scholar
[11] Shinkai G, Hayashi T, Ota T, Fujisawa T 2009 Phys. Rev. Lett. 103 056802
Google Scholar
[12] Makhlin Y, Shnirman A 2001 Rev. Mod. Phys. 73 357
Google Scholar
[13] Wu J L, Song C, Xu J 2016 Quantum Inf. Process 15 3663
Google Scholar
[14] Zhang X, Chen Y H, Wu Q C 2017 Laser Phys. 27 015202
Google Scholar
[15] Xu J, Yu L, Wu J L, Ji X 2017 Chin. Phys. B 26 090301
Google Scholar
[16] Berry M V 1987 Proc. R. Soc. Lond. A 414 31
Google Scholar
[17] Facchi P, Marmo G, Pascazio S 2009 J. Phys.: Conf. Ser. 196 012017
Google Scholar
[18] Shen L T, Wu H Z, Chen R X 2011 J. Phys. B 44 205503
Google Scholar
[19] Yang R C, Li G, Zhang T C 2013 Quantum. Inf. Process 12 493
Google Scholar
[20] Demirplak M, Rice S A 2008 J. Phys. Chem. A 129 154111
Google Scholar
[21] Demirplak M, Rice S A 2008 J. Chem. Phys. 116 8028
Google Scholar
-
图 1 制备超导三量子比特GHZ态的装置图
Figure 1. Setup for generating GHZ state of three superconducting qubits.
图 2
${\theta _0}(t)$ 和${\theta _1}(t)$ 随时间的变化情况Figure 2. Dependence on
$t$ of${\theta _0}(t)$ and${\theta _1}(t)$ .
图 3 保真度随
${\varOmega _0}$ 的变化情况Figure 3. Dependence on
${\varOmega _0}$ of fidelity ($\lambda = 100{t_{\rm f}}^{ - 1}$ ).
图 4 量子态布局随时间的变化
Figure 4. Population
${P_m}$ of$\left| {{\phi _m}} \right\rangle $ ($m = 1,2,$ 3, ···, 7) versus$t$ (${\varOmega _0} = 32.6{t_{\rm{f}}}^{ - 1},$ $\lambda = 100{t_{\rm{f}}}^{ - 1}$ ).
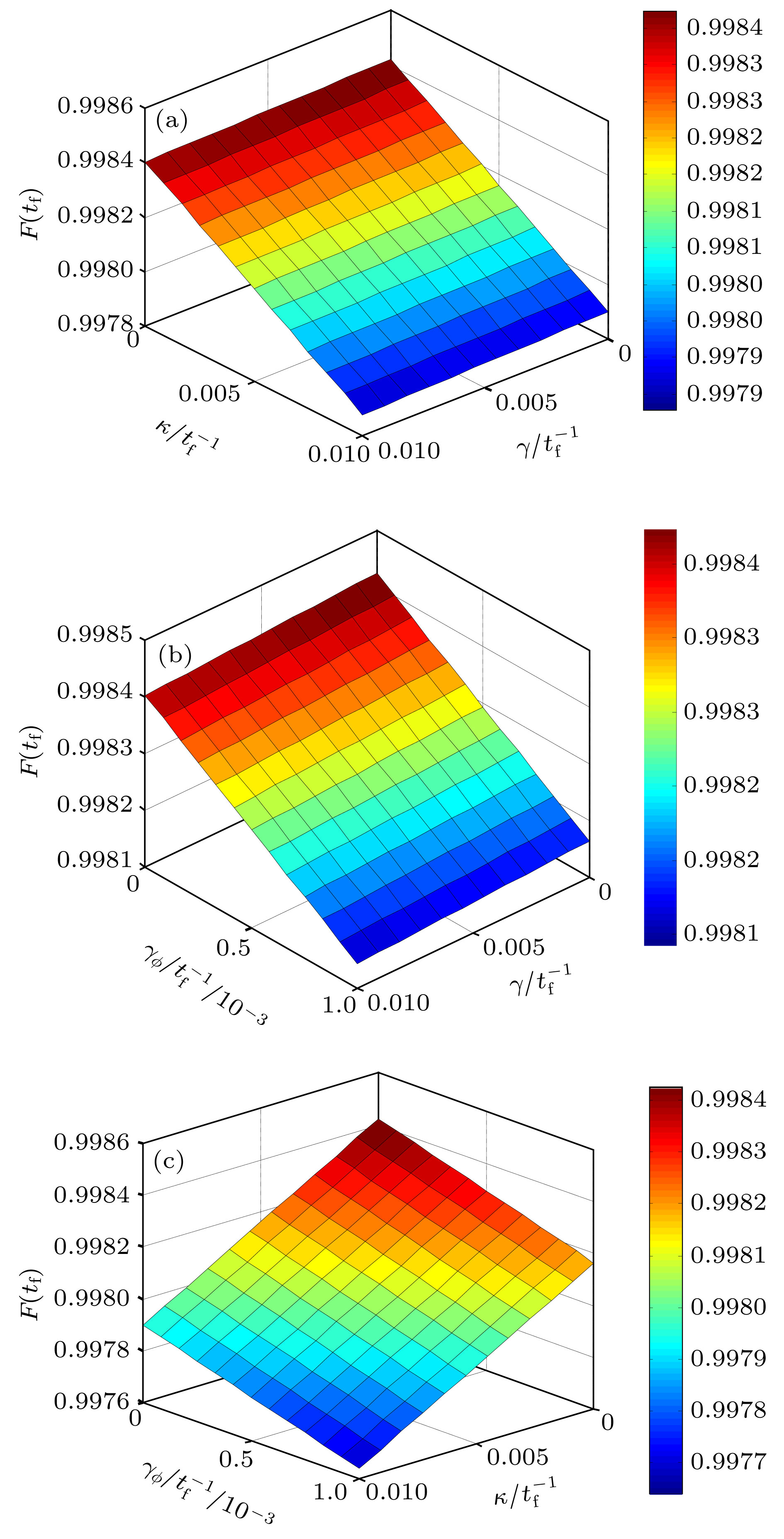
图 5 (a)
$\gamma $ 和$\kappa $ 对目标态保真度的影响; (b)${\gamma _\phi }$ 和$\gamma $ 对目标态保真度的影响; (c)$\kappa $ 和${\gamma _\phi }$ 对目标态保真度的影响Figure 5. (a) Denpendence on
$\gamma $ and$\kappa $ of fidelity; (b) denpendence on$\gamma $ and${\gamma _\phi }$ of fidelity; (c) dependence on$\kappa $ and${\gamma _\phi }$ of fidelity. -
[1] Li X H, Deng F G, Zhou H Y 2006 Phys. Rev. A 74 054302
Google Scholar
[2] Karlsson A, Bourennane M 1998 Phys. Rev. A 58 4394
Google Scholar
[3] Xiao L, Long G L, Deng F G, Pan J W 2004 Phys. Rev. A 69 052307
Google Scholar
[4] Zeilinger A, Horne M A, Weinfurter H 1997 Phys. Rev. Lett. 78 3031
Google Scholar
[5] Zheng S B 2001 Phys. Rev. Lett. 87 230404
Google Scholar
[6] Leibfriend D, Knill E, Seidelin S 2005 Nature 438 639
Google Scholar
[7] Su X L, Tan A, Jia X J 2007 Phys. Rev. Lett. 98 070502
Google Scholar
[8] Raimond J M, Brune M, Haroche S 2001 Rev. Mod. Phys. 73 565
Google Scholar
[9] Kang Y H, Chen Y H, Wu Q C 2016 Sci. Rep. 6 36737
Google Scholar
[10] Clarke J, Wilhelm F K 2008 Nature 453 1031
Google Scholar
[11] Shinkai G, Hayashi T, Ota T, Fujisawa T 2009 Phys. Rev. Lett. 103 056802
Google Scholar
[12] Makhlin Y, Shnirman A 2001 Rev. Mod. Phys. 73 357
Google Scholar
[13] Wu J L, Song C, Xu J 2016 Quantum Inf. Process 15 3663
Google Scholar
[14] Zhang X, Chen Y H, Wu Q C 2017 Laser Phys. 27 015202
Google Scholar
[15] Xu J, Yu L, Wu J L, Ji X 2017 Chin. Phys. B 26 090301
Google Scholar
[16] Berry M V 1987 Proc. R. Soc. Lond. A 414 31
Google Scholar
[17] Facchi P, Marmo G, Pascazio S 2009 J. Phys.: Conf. Ser. 196 012017
Google Scholar
[18] Shen L T, Wu H Z, Chen R X 2011 J. Phys. B 44 205503
Google Scholar
[19] Yang R C, Li G, Zhang T C 2013 Quantum. Inf. Process 12 493
Google Scholar
[20] Demirplak M, Rice S A 2008 J. Phys. Chem. A 129 154111
Google Scholar
[21] Demirplak M, Rice S A 2008 J. Chem. Phys. 116 8028
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 7046
- PDF Downloads: 71
- Cited By: 0
