-
As an important quantity in the field of parameter estimation theory and quantum precision measurement, quantum Fisher information (QFI) can not only be used to set the theoretical limit of measurement precision in quantum system, but also be exploited to witness metrological useful quantum entanglement. Recently, it has also been broadly used in many aspects of quantum information science, including quantum metrology, multipartite entanglement structure detection, quantum phase transition, quantum chaos, quantum computation and etc. In this work, from the perspective of quantum measurement, we study the quantum Fisher information of an N-qubit WV state (
$\alpha \left\vert W_N \right\rangle +\sqrt{1-\alpha^2}\left\vert 00\cdots0\right\rangle$ ) under local operation and Lipkin-Meshkov-Glick (LMG) model. Furthermore, with the general Cramér-Rao lower bound (CRLB) we analyze its performance in high-precision phase measurement. The results show that, under the local operation, the QFI of an N-qubit WV state becomes larger with the increase of parameter α. This not only means the enhanced quantum entanglement, but also implies the powerful ability in high-precision quantum measurement. In the LMG model, as the increase of interactional strength γ the QFI of$N=3$ qubits WV state gradually tends to be stable and almost not be affected by parameter α, which relaxes the requirement in the preparation of target state and indicates a great potential in achieving the relatively stable measurement precision. When the number of qubits from WV state is larger than 3, the QFI of WV state increases with the increase of parameter α. In the case of fixed parameter α, we investigate the QFI of an N-qubit WV state with respect to interaction strength γ. It is found that the QFI of WV state will increase with the increasing interaction strength, which implies that the greater the interaction strength, the stronger the quantum measurement ability of the WV state. Our work will promote the development of high-precision quantum metrology and especially the interaction-enhanced quantum measurement, and further provide new insights in quantum information processing.-
Keywords:
- quantum Fisher information /
- WV state /
- Lipkin-Meshkov-Glick model /
- precision measurement
[1] Fisher R A 1912 Messenger of Mathematics 41 155
[2] Helstrom C W 1976 Quantum Detection and Estimation Theory (New York: Academic Press) pp235–293
[3] Holevo A S 1982 Probabilistic and Statistical Aspects of Quantum Theory (Amsterdam: North Holland) pp52–96
[4] Kreutz C, Timmer J 2013 Optimal Experiment Design, Fisher Information. In: Dubitzky W, Wolkenhauer O, Cho K H, Yokota H, editors. Encyclopedia of Systems Biology (New York: Springer) pp1576–1579
[5] Ly A, Marsman M, Verhagen J, Grasman R P, and Wagenmakers E J 2017 J. Math. Psychol. 80 40
Google Scholar
[6] Giovannetti V, Lloyd S, Maccone L 2006 Phys. Rev. Lett. 96 010401
Google Scholar
[7] Li Y, Pezzè L, Li W D, Smerzi A 2019 Phys. Rev. A 99 022324
Google Scholar
[8] Fiderer L J, E. Fraïsse J M, Braun D 2019 Phys. Rev. Lett. 123 250502
Google Scholar
[9] Li Y, Ren Z H 2023 Phys. Rev. A 107 012403
Google Scholar
[10] Yin P, Zhao X B, Yang Y X, Guo Y, Zhang W H, Li G C, Han Y J, Liu B H, Xu J S, Chiribella G, Chen G, Li C F, Guo G C 2023 Nat. Phys. 19 1122
Google Scholar
[11] Li Y, Pezze L, Gessner M, Ren Z H, Li W D, Smerzi A 2018 Entopy 20 628
Google Scholar
[12] Braunstein S L, Caves C M 1994 Phys. Rev. Lett. 72 3439
Google Scholar
[13] Wootters W K 1981 Phys. Rev. D 23 357
Google Scholar
[14] Pezzè L, Smerzi A 2009 Phys. Rev. Lett. 102 100401
Google Scholar
[15] Hyllus P, Laskowski W, Krischek R, Schwemmer C, Wieczorek W, Weinfurter H, Pezzè L, Smerzi A 2012 Phys. Rev. A 85 022321
Google Scholar
[16] Pezzè L, Smerzi A, Oberthaler M K, Schmied R, Treutlein P 2018 Rev. Mod. Phys. 90 035005
Google Scholar
[17] 任志红, 李岩, 李艳娜, 李卫东 2019 68 040601
Google Scholar
Ren Z H, Li Y, Li Y N, Li W D 2019 Acta Phys. Sin. 68 040601
Google Scholar
[18] Zanardi P, Paris M G A, Venuti L C 2008 Phys. Rev. A 78 042105
Google Scholar
[19] Hauke P, Heyl M, Tagliacozzo L, Zoller P 2016 Nat. Phys. 12 778
Google Scholar
[20] Gabbrielli M, Smerzi A, Pezzé L 2018 Sci. Rep. 8 15663
Google Scholar
[21] Gietka K, Ruks L, Busch T 2022 Quantum 6 700
Google Scholar
[22] Gühne O, Tòth G 2009 Phys. Rep. 474 1
Google Scholar
[23] Pezzè L, Li Y, Li W D, Smerzi A 2016 Proc. Natl. Acad. Sci. 113 11459
Google Scholar
[24] Li Y and Li P F 2020 Phys. Lett. A 384 126413
Google Scholar
[25] Ren Z H, Li W D, Smerzi A, Gessner M 2021 Phys. Rev. Lett. 126 080502
Google Scholar
[26] Li Y, Ren Z H 2022 Physica A 596 127137
Google Scholar
[27] 宋立军, 严冬, 刘烨 2011 60 120302
Google Scholar
Song L J, Yan D, Liu Y 2011 Acta. Phys. Sin. 60 120302
Google Scholar
[28] Wang X Q, Ma J, Zhang X H, Wang X G 2011 Chin. Phys. B 20 050510
Google Scholar
[29] Berrada K, Abdel-Khalek S, Khalil E M, Alkaoud A, Eleuch H 2022 Chaos, Solitons Fractals 164 112621
Google Scholar
[30] Meyer J J 2021 Quantum 5 539
Google Scholar
[31] Yu M, Li D, Wang J, Chu Y M, Yang P, Gong M, Goldman N, Cai J M 2021 Phys. Rev. Res. 3 043122
Google Scholar
[32] Jin H C, Jeong S K 2015 Phys. Rev. A 92 042307
Google Scholar
[33] Shi X, Chen L 2020 Phys. Rev. A 101 032344
Google Scholar
[34] Shi X 2020 Phys. Lett. A 384 126392
Google Scholar
[35] Lai L M, Fei S M, Wang Z X 2021 J. Phys. A 54 425301
Google Scholar
[36] Jarzyna M, Demkowicz-Dobrzanski R 2015 New J. Phys. 17 013010
Google Scholar
[37] Lipkin H J, Meshkov N, Glick A 1965 Nucl. Phys. 62 188
Google Scholar
-
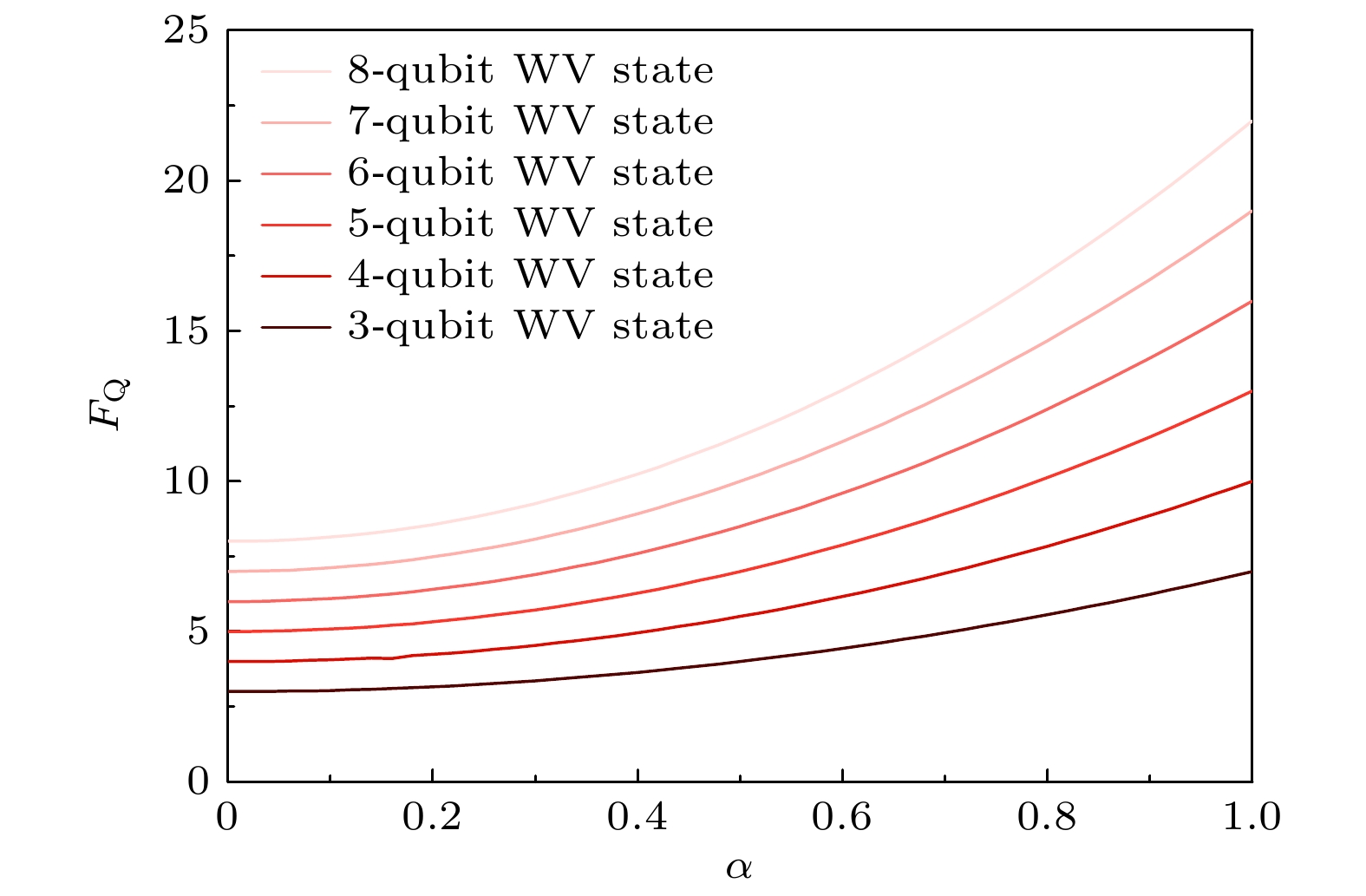
图 1 N量子比特WV态在局域操作下的量子Fisher信息随参数α的变化. 从下(黑色实线)到上(浅粉色实线)分别表示3量子比特WV态到8量子比特WV态的结果
Figure 1. Quantum Fisher information of an N-qubit WV state with respect to α under local operation. From bottom (black line) to top (light pink line) it respectively denotes the result from 3-qubit WV state to 8-qubit WV state.
图 2 量子比特WV态在LMG模型下的量子Fisher信息随参数α的变化 (a) 3比特; (b) 4比特; (c) 5比特; (d) 6比特
Figure 2. Quantum Fisher information of qubit WV state with respect to α in the LMG model: (a) 3-qubit; (b) 4-qubit; (c) 5-qubit; (d) 6-qubit.
图 3 量子比特WV态在LMG模型下的量子Fisher信息随相互作用强度γ的变化 (a) 3比特; (b) 4比特; (c) 5比特; (d) 6比特
Figure 3. Quantum Fisher information of qubit WV state with respect to interactional strength γ in the LMG model: (a) 3-qubit; (b) 4-qubit; (c) 5-qubit; (d) 6-qubit.
-
[1] Fisher R A 1912 Messenger of Mathematics 41 155
[2] Helstrom C W 1976 Quantum Detection and Estimation Theory (New York: Academic Press) pp235–293
[3] Holevo A S 1982 Probabilistic and Statistical Aspects of Quantum Theory (Amsterdam: North Holland) pp52–96
[4] Kreutz C, Timmer J 2013 Optimal Experiment Design, Fisher Information. In: Dubitzky W, Wolkenhauer O, Cho K H, Yokota H, editors. Encyclopedia of Systems Biology (New York: Springer) pp1576–1579
[5] Ly A, Marsman M, Verhagen J, Grasman R P, and Wagenmakers E J 2017 J. Math. Psychol. 80 40
Google Scholar
[6] Giovannetti V, Lloyd S, Maccone L 2006 Phys. Rev. Lett. 96 010401
Google Scholar
[7] Li Y, Pezzè L, Li W D, Smerzi A 2019 Phys. Rev. A 99 022324
Google Scholar
[8] Fiderer L J, E. Fraïsse J M, Braun D 2019 Phys. Rev. Lett. 123 250502
Google Scholar
[9] Li Y, Ren Z H 2023 Phys. Rev. A 107 012403
Google Scholar
[10] Yin P, Zhao X B, Yang Y X, Guo Y, Zhang W H, Li G C, Han Y J, Liu B H, Xu J S, Chiribella G, Chen G, Li C F, Guo G C 2023 Nat. Phys. 19 1122
Google Scholar
[11] Li Y, Pezze L, Gessner M, Ren Z H, Li W D, Smerzi A 2018 Entopy 20 628
Google Scholar
[12] Braunstein S L, Caves C M 1994 Phys. Rev. Lett. 72 3439
Google Scholar
[13] Wootters W K 1981 Phys. Rev. D 23 357
Google Scholar
[14] Pezzè L, Smerzi A 2009 Phys. Rev. Lett. 102 100401
Google Scholar
[15] Hyllus P, Laskowski W, Krischek R, Schwemmer C, Wieczorek W, Weinfurter H, Pezzè L, Smerzi A 2012 Phys. Rev. A 85 022321
Google Scholar
[16] Pezzè L, Smerzi A, Oberthaler M K, Schmied R, Treutlein P 2018 Rev. Mod. Phys. 90 035005
Google Scholar
[17] 任志红, 李岩, 李艳娜, 李卫东 2019 68 040601
Google Scholar
Ren Z H, Li Y, Li Y N, Li W D 2019 Acta Phys. Sin. 68 040601
Google Scholar
[18] Zanardi P, Paris M G A, Venuti L C 2008 Phys. Rev. A 78 042105
Google Scholar
[19] Hauke P, Heyl M, Tagliacozzo L, Zoller P 2016 Nat. Phys. 12 778
Google Scholar
[20] Gabbrielli M, Smerzi A, Pezzé L 2018 Sci. Rep. 8 15663
Google Scholar
[21] Gietka K, Ruks L, Busch T 2022 Quantum 6 700
Google Scholar
[22] Gühne O, Tòth G 2009 Phys. Rep. 474 1
Google Scholar
[23] Pezzè L, Li Y, Li W D, Smerzi A 2016 Proc. Natl. Acad. Sci. 113 11459
Google Scholar
[24] Li Y and Li P F 2020 Phys. Lett. A 384 126413
Google Scholar
[25] Ren Z H, Li W D, Smerzi A, Gessner M 2021 Phys. Rev. Lett. 126 080502
Google Scholar
[26] Li Y, Ren Z H 2022 Physica A 596 127137
Google Scholar
[27] 宋立军, 严冬, 刘烨 2011 60 120302
Google Scholar
Song L J, Yan D, Liu Y 2011 Acta. Phys. Sin. 60 120302
Google Scholar
[28] Wang X Q, Ma J, Zhang X H, Wang X G 2011 Chin. Phys. B 20 050510
Google Scholar
[29] Berrada K, Abdel-Khalek S, Khalil E M, Alkaoud A, Eleuch H 2022 Chaos, Solitons Fractals 164 112621
Google Scholar
[30] Meyer J J 2021 Quantum 5 539
Google Scholar
[31] Yu M, Li D, Wang J, Chu Y M, Yang P, Gong M, Goldman N, Cai J M 2021 Phys. Rev. Res. 3 043122
Google Scholar
[32] Jin H C, Jeong S K 2015 Phys. Rev. A 92 042307
Google Scholar
[33] Shi X, Chen L 2020 Phys. Rev. A 101 032344
Google Scholar
[34] Shi X 2020 Phys. Lett. A 384 126392
Google Scholar
[35] Lai L M, Fei S M, Wang Z X 2021 J. Phys. A 54 425301
Google Scholar
[36] Jarzyna M, Demkowicz-Dobrzanski R 2015 New J. Phys. 17 013010
Google Scholar
[37] Lipkin H J, Meshkov N, Glick A 1965 Nucl. Phys. 62 188
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 3289
- PDF Downloads: 99
- Cited By: 0
