Research progress of rare earth magnetic materials based on machine learning

LIU Dan; LI Yuan; SUN Ruoxuan; QI Xing; SHEN Baogen

doi:10.7498/aps.74.20250431

Abstract
Rare-earth elements possess unique atomic structures characterized by multiple unpaired 4f orbital electrons in inner shells, high atomic magnetic moments, and strong spin-orbit coupling. These attributes endow them with rich electronic energy levels, enabling them to form compounds with different valence states and coordination environments. Consequently, rare-earth materials typically exhibit excellent magnetic properties and complex magnetic domain structures, making them critical for the development of high-tech industries. The intricate magnetic configurations, different types of magnetic coupling, and direct/indirect magnetic exchange interactions in these materials not only facilitate the development of novel functional devices but also pose significant challenges to fundamental research. With the rapid advancement of data mining techniques, the emergence of big data and artificial intelligence provides researchers with a new method to efficiently analyze vast experimental and computational datasets, thereby accelerating the exploration and development of rare-earth magnetic materials. This work focuses on rare-earth permanent magnetic materials, rare-earth magnetocaloric materials, and rare-earth magnetostrictive materials, detailing the application progress of data mining techniques in property prediction, composition and process optimization, and microstructural analysis. This work also delves into the current challenges and future trends, aiming to provide a theoretical foundation for deepening the integration of data mining technologies with rare-earth magnetic material research.

Keywords:
data mining /

rare earth magnetic material /

machine learning /

performance prediction
FullText HTML

Cited By

图 1 (a) 不同机器学习算法的训练集预测结果对比; (b) 钕铁硼快淬带矫顽力H_cj和最大磁能积(BH)_max的预测图及其性价比等高线^[12]

Figure 1. (a) Predicted scatter plots of different machine learning algorithms; (b) predicted maps of H_cj and (BH)_max of Nd-Fe-B meltspun magnets, and their corresponding cost performances^[12].

DownLoad: Full-Size Img PowerPoint

图 2 原子特征之间的Pearson相关系数热图^[15]

Figure 2. Heatmap of the Pearson correlation coefficients between atomic characteristics^[15].

DownLoad: Full-Size Img PowerPoint

图 3 基于高通度实验和机器学习的La-Co取代锶六铁氧体磁性能预测与组成设计^[17]

Figure 3. Magnetic properties prediction and composition design of La-Co substitution Sr-hexaferrite based on high-through experiments and machine learning^[17].

DownLoad: Full-Size Img PowerPoint

图 4 (a) 不同Sm-Co合金的热重分析微分曲线; (b) 实验测量和逻辑回归模型预测的T_c^[19]

Figure 4. (a) DTG curves of the Sm-Cobased alloys prepared in experiments; (b) the T_c values from experimental measurements and from the model predictions^[19].

DownLoad: Full-Size Img PowerPoint

图 5 随机森林算法对稀土过渡族金属居里温度T_c的预测值、绝对误差分布和相对误差分布^[20]

Figure 5. Model output from Random Forest algorithm for T_c, absolute error, and relative error^[20].

DownLoad: Full-Size Img PowerPoint

图 6 支持向量回归模型对Ba_1–xLa_xFe_12–yMn_yO₁₉铁氧体　(a) M_s; (b) H_c; (c) K₁; (d) H_a的预测图^[22]

Figure 6. Prediction diagram of (a) M_s, (b) H_c, (c) K₁ and (d) H_a of Ba_1–xLa_xFe_12–yMn_yO₁₉ ferrite by SVR^[22].

DownLoad: Full-Size Img PowerPoint

图 7 支持向量回归模型(SVR)在μ₀M, K₁和E_f上的十折交叉验证结果^[24]

Figure 7. Results of the tenfold cross validation of the SVR models for μ₀M, K₁, and E_f^[24].

DownLoad: Full-Size Img PowerPoint

图 8 将均值漂移理论应用于成分扩展晶圆的衍射图谱, 用于快速分析相分布^[25]

Figure 8. Mean shift theory as applied to diffraction patterns taken from a composition spread wafer for rapid phase distribution analysis^[25].

DownLoad: Full-Size Img PowerPoint

图 9 ML-AGA-DFT反馈循环中获得的7种有应用潜力的永磁体Fe-Co-B化合物的晶体结构^[27]

Figure 9. Crystal structures of seven promising Fe-Co-B compounds for permanent magnet obtained from our ML-AGA-DFT predictions^[27].

DownLoad: Full-Size Img PowerPoint

图 10 (a) 0—2 T和(c) 0—5 T下最大磁熵变(ΔS_M)_max的数据分布; (b) 0—2 T和(d) 0—5 T预测模型的训练性能表现, 红星为最佳参数组合^[29]

Figure 10. Data distribution for (ΔS_M)_max at (a) 0–2 T and (c) 0–5 T; performances of prediction models at (b) 0–2 T and (d) 0–5 T trained with different parameters combinations, respectively^[29].

DownLoad: Full-Size Img PowerPoint

图 11 随机森林模型对材料磁熵变-ΔS_M的预测结果　(a) 数据集中所有材料-ΔS_M的实验值和预测值对比; (b) 测试集中按材料类型细分的实验-ΔS_M与预测对比^[30]

Figure 11. RF model for -ΔS_M of magnetocaloric materials: (a) Experimental vs predicted -ΔS_M for the materials in dataset; (b) experimental vs predicted -ΔS_M in the test set by material type breakdown^[30].

DownLoad: Full-Size Img PowerPoint

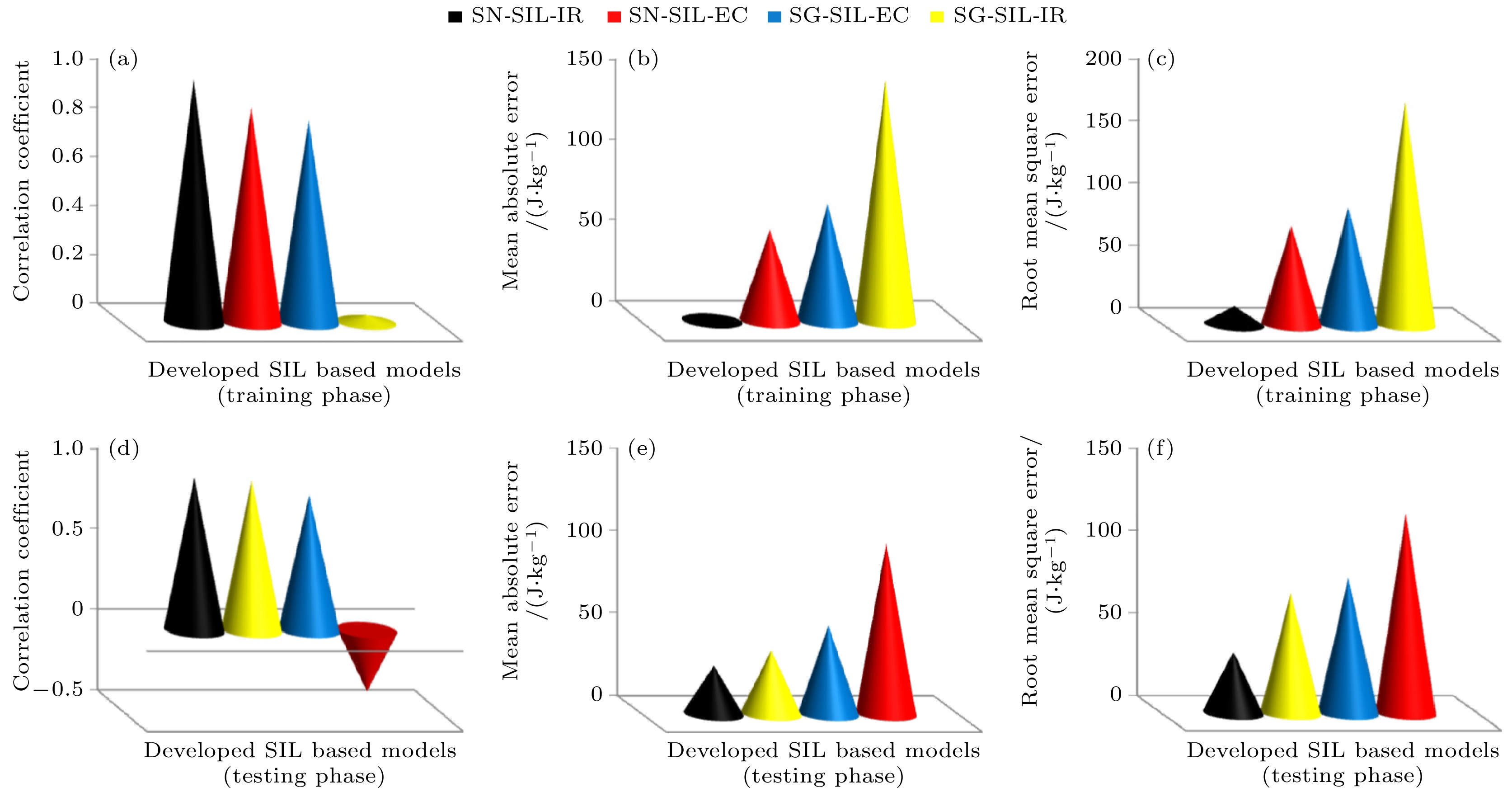
图 12 单隐层模型SIL的泛化能力评估　(a) 训练样本的相关系数; (b) 训练样本的平均绝对误差; (c) 训练样本的均方根误差; (d) 测试样本的相关系数; (e) 测试样本的平均绝对误差; (f) 测试样本的均方根误差^[31]

Figure 12. Generalization capacity evaluation of developed SIL-based models: (a) Training samples coefficient of correlation, (b) training samples mean absolute error, (c) training samples root mean square error, (d) testing samples coefficient of correlation, (e) testing samples mean absolute error, (f) testing samples root mean square error^[31].

DownLoad: Full-Size Img PowerPoint

图 13 机器学习模型在预测稀土基三元金属间化合物时的性能比较^[32]　(a) 均方根误差; (b) 相关系数; (c) 平均绝对误差

Figure 13. Performance of the intelligent models and their comparison for testing ternary intermetallic magnetocaloric compounds^[32]: (a) Root mean square error; (b) correlation coefficient; (c) mean absolute error.

DownLoad: Full-Size Img PowerPoint

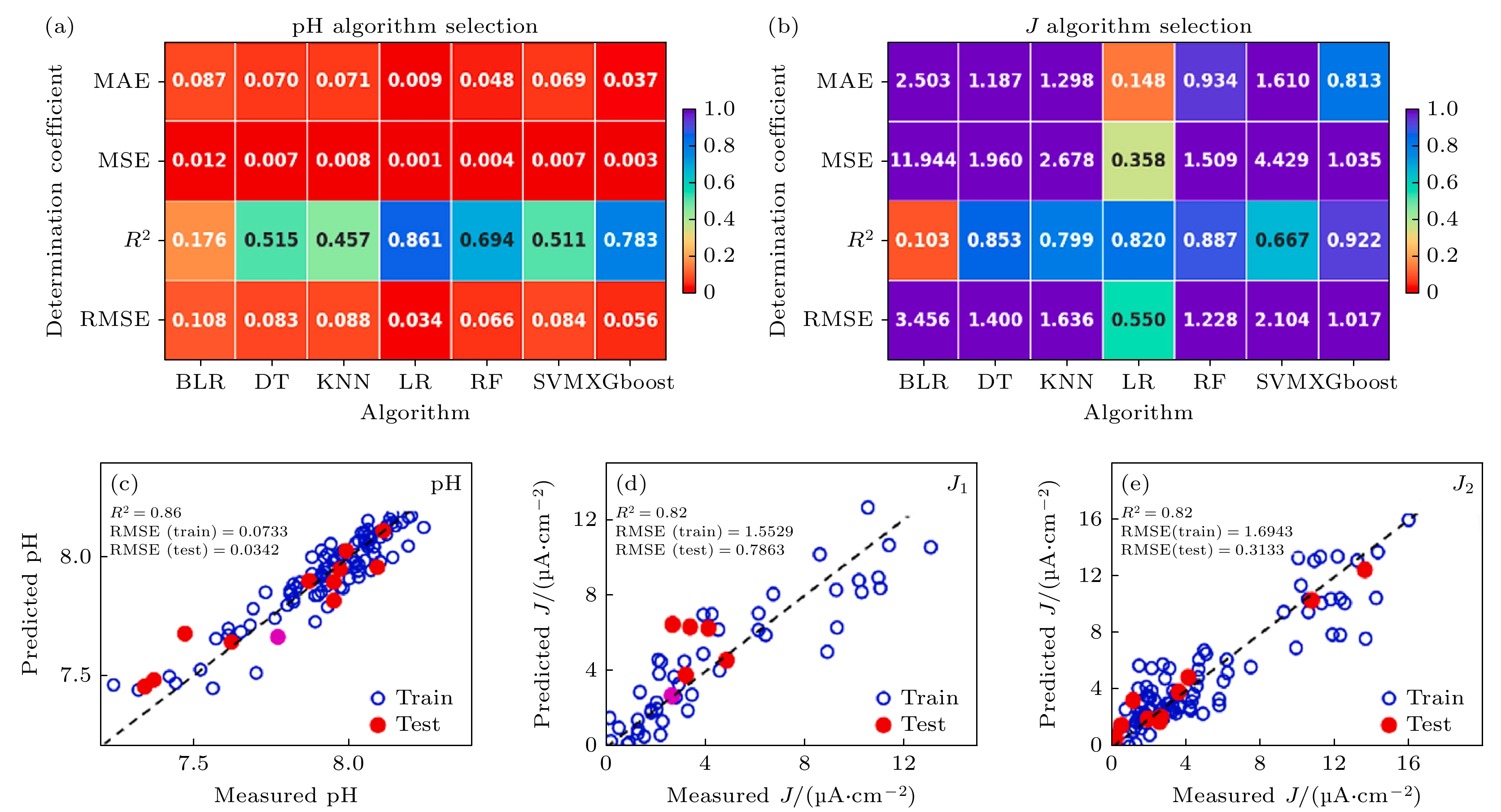
图 14 ML建模过程及缓蚀剂最佳配比的求解^[33]　(a) 酸碱度pH算法选择; (b) 腐蚀电流密度J算法选择; (c) 基于线性回归算法pH值的预测值与测量值对比; (d) 基于线性回归算法的J₁值; (e) J₂值的预测值与测量值对比

Figure 14. ML modeling process and solving the optimal composition of corrosion inhibitor^[33]: (a) The pH model algorithm selection; (b) J model algorithm selection; (c) measured-predicted pH value plot for LR algorithm; (d) measured-predicted J₁ value plot for LR algorithm; (e) measured-predicted J₂ value plot for LR algorithm.

DownLoad: Full-Size Img PowerPoint

图 15 (a) 三步特征选择流程图; (b) 随机森林特征选择; (c) 穷举筛选^[35]

Figure 15. (a) Flowchart of three-step feature selection; (b) feature selection by random forest; (c) exhaustive screening^[35].

DownLoad: Full-Size Img PowerPoint

图 17 (a) 10种机器学习算法对磁性合金M_s和硬度的均方根误差RMSE; (b), (c) M_s和硬度H的预测值与实验值对比^[40]

Figure 17. (a) RMSE score of models based on ten ML algorithms; (b), (c) precietd values of M_s and hardness compared with the corresponding experimental values^[40].

DownLoad: Full-Size Img PowerPoint

图 16 神经网络在预测材料是否具有(a)—(c) 非线性磁结构和(d)—(f) 斯格明子结构的表现^[39]

Figure 16. Performance of Neural Networks in predicting whether a material has (a)–(c) nonlinear magnetic structure and (d)–(f) Skoming substructure^[39].

DownLoad: Full-Size Img PowerPoint

表 1 常用的机器学习算法的优势与缺陷

Table 1. Advantages and disadvantages of commonly used machine learning algorithms.

模型	优势	不足
MLR	简单易懂, 计算效率高; 可解释性强, 参数直接反映特征重要性	无法捕捉非线性关系; 对异常值敏感
SVM	擅长处理高维空间中的非线性分类; 小样本数据表现优异	核函数选择依赖经验; 计算成本高, 扩展性差
DT	无需数据标准化; 可视化清晰; 擅长处理分类问题	易过拟合, 需剪枝优化; 对连续特征处理能力有限
RF	抗过拟合能力强, 适合高维数据; 可输出特征重要性, 便于特征选择	计算复杂度较高; 对小样本数据表现不佳
K-means	无需标注数据, 自动发现数据模式; 计算效率高	需要预先指定聚类数
GA	全局搜索能力, 避免局部最优; 并行处理, 适合高维问题	计算成本高; 复杂问题的收敛速度慢; 依赖高质量的训练数据
粒子群优化算法(PSO)	适用于目标函数不连续的场景; 参数少, 易于与实验工具集成	收敛速度慢; 参数敏感性; 局部搜索能力弱
PCA	有效降维, 保留关键信息; 可视化高维数据的潜在结构	无法捕捉非线性关系; 忽略特征间的相关性
ANN	强大的非线性建模能力; 适用于复杂模式识别, 如图像、分子结构	需要大量数据和计算资源; 可解释性差, 存在 “黑箱” 问题
CNN	无需人工设计特征; 擅长高维数据处理; 鲁棒性强	计算资源需求大; 数据依赖性; 解释性差

DownLoad: CSV

map

[1]	中华人民共和国国务院2024-06-29 稀土管理条例 https://www.gov.cn/zhengce/zhengceku/202406/content_6960153.htm
[2]	中华人民共和国国务院 2023-12-26中华人民共和国国民经济和社会发展第十四个五年规划和2035年远景目标纲要 https://www.gov.cn/zhuanti/shisiwuguihua/sdb.htm
[3]	Tai D Q, Li B, Xue H Y, Zheng T, Wu J G 2024 Acta Mater. 262 119411 Google Scholar
[4]	Swamynadhan M J, O'Hara A, Ghosh S, Pantelides S T 2024 Adv. Funct. Mater. 34 2400195 Google Scholar
[5]	Ding S L, Kang M G, Legrand W, Gambardella P 2024 Phys. Rev. Lett. 132 236702 Google Scholar
[6]	邓祥文, 伍力源, 赵锐, 王嘉鸥, 赵丽娜 2024 73 210701 Google Scholar Deng X W, Wu L Y, Zhao R, Wang J O, Zhao L N 2024 Acta Phys. Sin. 73 210701 Google Scholar
[7]	Möller J J, Körner W, Krugel G , Urban D F, Elsässer C 2018 Acta Mater. 153 53
[8]	Butler K T, Davies D W, Cartwright H, Isayev O, Walsh A. Nature 559 547
[9]	张桥, 谭薇, 宁勇祺, 聂国政, 蔡孟秋, 王俊年, 朱慧平, 赵宇清 2024 73 230201 Google Scholar Zhang Q, Tan W, Ning Y Q, Nie G Z, Cai M Q, Wang J N, Zhu H P, Zhao Y Q 2024 Acta Phys. Sin. 73 230201 Google Scholar
[10]	Wang Z, Sun Z H, Yin H, Liu X H, Wang J L, Zhao H T, Pang C H, Wu T, Li S Z, Yin Z Y, Yu X F 2022 Adv. Mater. 34 2104113 Google Scholar
[11]	彭向凯, 吉经纬, 李琳, 任伟, 项静峰, 刘亢亢, 程鹤楠, 张镇, 屈求智, 李唐, 刘亮, 吕德胜 2019 68 130701 Google Scholar Peng X K, Ji J W, Li L, Ren W, Xiang J F, Liu K K, Cheng H N, Zhang Z, Qu Q Z, Li T, Liu L, Lü D S 2019 Acta Phys. Sin. 68 130701 Google Scholar
[12]	李锐 2018博士学位论文(北京: 中国科学院大学) Li R 2018 Ph. D. Dissertation (Beijing: University of Chinese Academy of Sciences
[13]	Kovacs A, Fischbacher J, Oezelt H, Kornell A, Ali Q, Gusenbauer M, Yano M, Sakuma N, Kinoshita A, Shoji T, Kato A, Hong Y, Grenier S, Devillers T, Dempsey N M, Fukushima T, Akai H, Kawashima N, Miyake T, Schrefl T 2023 Front. Mater. 9 1094055 Google Scholar
[14]	Hosokawa H, Calvert E L, Shimojima K 2021 J. Magn. Magn. Mater. 526 167651 Google Scholar
[15]	Guo K, Lu H, Zhao Z, Tang F W, Wang H B, Song X Y 2022 Comp. Mater. Sci. 205 111232 Google Scholar
[16]	Wen J T, Hu H G, An J S, Han T, Hu J F 2024 J. Supercond. Nov. Magn. 37 1443 Google Scholar
[17]	Liu R S, Wang L C, Xu Z Y, Qin C Y, Li Z Y, Yu X, Liu D, Gong H Y, Zhao T Y, Sun J R, Hu F X, Shen B G 2022 Mater. Today Commun. 32 103996 Google Scholar
[18]	Nguyen D N, Pham T L, Nguyen V C, Kino H, Miyake T, Dam H C 2019 J. Phys. Mater. 2 034009 Google Scholar
[19]	Xu G J, Cheng F, Lu H, Hou C, Song X Y 2024 Acta Mater. 274 120026 Google Scholar
[20]	Halder A, Rom S, Ghosh A, Dasgupta T S 2020 Phys. Rev. Appl. 14 034024 Google Scholar
[21]	Lambard G, Sasakib T T, Sodeyama K, Ohkubo T, Hono K 2022 Scripta Mater. 209 114341 Google Scholar
[22]	Lu S F, Liu Y L, Yin Q S, Chen J F, Wu J, Li J, Zhan P J, Chen Z C 2024 J. Eur. Ceram. Soc. 44 5677 Google Scholar
[23]	Choudhary A K, Grubesa T, Jansche A, Bernthaler T, Goll D, Schneider G 2024 Acta Mater. 264 119563 Google Scholar
[24]	Möller J J, Körner W, Krugel G, Urban D F, Elsässer C 2018 Acta Mater. 153 53 Google Scholar
[25]	Kusne A G, Gao T, Mehta A, Ke L Q, Nguyen M C, Ho K M, Antropov V, Wang C Z, Kramer M J, Long C, Takeuchi I 2014 Sci. Rep. 4 63
[26]	Nieves P, Arapan S, Hadjipanayis G C, Niarchos D, Barandiaran J M, Cuesta-López S 2016 Phys. Status Solidi C 13 942 Google Scholar
[27]	Xia W Y, Sakurai M, Balasubramanian B, Liao T, Wang R H, Zhang C, Sun H J, Ho K M, Chelikowsky J R, Sellmyer D J, Wang C Z 2022 Proc. Natl. Acad. Sci. 119 2204485119 Google Scholar
[28]	Zhang B, Zheng X Q, Zhao T Y, Hu F X, Sun J R, Shen B G 2018 Chinese Phys. B 27 067503 Google Scholar
[29]	张博 2018博士学位论文(北京: 中国科学院大学) Zhang B. 2018 Ph. D. Dissertation (Beijing: University of Chinese Academy of Sciences
[30]	Ucar H, Paudyal D, Choudhary K 2022 Comp. Mater. Sci. 209 111414 Google Scholar
[31]	Alqahtani A 2024 Sustainability 16 1542 Google Scholar
[32]	Shamsah S M I 2024 Int. J. Refrig. 168 122 Google Scholar
[33]	Zhao Q, Yan K L, Cui Z, Wen B Y, Xue F, Li J T, Guo J N, Xu A, Qiao K M, Ye R C, Long Y, Zhang D W, Luo H, Taskaev S, Zhang H 2023 Corros. Sci. 216 111115 Google Scholar
[34]	Gong J H, Zhang Z M, Zhang C L, Hu P Q, Zhou C, Wang D H, Yang S 2024 Rare Met. 43 2251 Google Scholar
[35]	Hu P Q, Zhou C, Zhang R S, Ding S D, Guo Y J, Wang B, Xue D Z, Ma Y Z, Dai Z Y, Zhang Y, Tian F H, Yang S 2025 Mater. Design 252 113799 Google Scholar
[36]	Foggiatto A L, Mizutori Y, Yamazaki T, Sato S, Masuzawa K, Nagaoka R, Taniwaki M, Fujieda S, Suzuki S, Ishiyama K, Fukuda T, Igarashi Y, Mitsumata C, Kotsugi M 2023 IEEE T. Magn. 59 2501604
[37]	黎威, 龙连春, 刘静毅, 杨洋 2022 71 060202 Google Scholar Li W, Long L C, Liu J Y, Yang Y 2022 Acta Phys. Sin. 71 060202 Google Scholar
[38]	Liu D, Liu Z X, Zhang J E, Yin Y N, Xi J F, Wang L C, Xiong J F, Zhang M, Zhao T Y, Jin J Y, Sun J R, Hu F X, Shen J, Shen B G 2023 Research 6 0082 Google Scholar
[39]	Liu D, Song J H, Liu Z X, Zhang J E, Chen W Q, Yin Y N, Xi J F, Zheng X Q, Hao J Z, Zhao T Y, Hu F X, Sun J R, Shen B G 2025 Mater. Design 251 113710 Google Scholar
[40]	Li X, Shek C H, Liaw P K, Shan G C 2024 Prog. Mater. Sci. 146 101332 Google Scholar

[1]	ZHANG Tong, WANG Jiahao, TIAN Shuai, SUN Xuran, LI Ri. Machine learning-based study of dynamic shrinkage behavior during solidification of castings. Acta Physica Sinica, doi: 10.7498/aps.74.20241581
[2]	WANG Peng, MAIMAITINIYAZI Maimaitiabudula. Quantum dynamics of machine learning. Acta Physica Sinica, doi: 10.7498/aps.74.20240999
[3]	ZHANG Suncheng, HAN Tongwei, WANG Rumeng, YANG Yantao, ZHANG Xiaoyan. Prediction and optimization of negative Poisson’s ratio in rhombic perforated graphene based on machine learning. Acta Physica Sinica, doi: 10.7498/aps.74.20241624
[4]	WU Yanghai, DU Hailong, XUE Lei, LI Jiaxian, XUE Miao, ZHENG Guoyao. Machine learning-based prediction of heat load on Tokamak divertor target plates. Acta Physica Sinica, doi: 10.7498/aps.74.20250381
[5]	GAO Yukun, ZHAO Jie, ZHOU Jingjing, ZHOU Jing. Finite element prediction and device performance of piezoelectric fiber composite based smart sensor. Acta Physica Sinica, doi: 10.7498/aps.74.20241379
[6]	QIN Chenglong, ZHAO Liang, JIANG Gang. Machine learning model predicted thermodynamic stability of rare earth compounds. Acta Physica Sinica, doi: 10.7498/aps.74.20250362
[7]	Zhang Xu, Ding Jin-Min, Hou Chen-Yang, Zhao Yi-Ming, Liu Hong-Wei, Liang Sheng. Machine learning based laser homogenization method. Acta Physica Sinica, doi: 10.7498/aps.73.20240747
[8]	Zhang Jia-Hui. Machine learning for in silico protein research. Acta Physica Sinica, doi: 10.7498/aps.73.20231618
[9]	Song Rui, Liu Xue-Mei, Wang Hai-Bin, Lü Hao, Song Xiao-Yan. Hardness prediction of WC-Co cemented carbide based on machine learning model. Acta Physica Sinica, doi: 10.7498/aps.73.20240284
[10]	Zhang Qiao, Tan Wei, Ning Yong-Qi, Nie Guo-Zheng, Cai Meng-Qiu, Wang Jun-Nian, Zhu Hui-Ping, Zhao Yu-Qing. Prediction of magnetic Janus materials based on machine learning and first-principles calculations. Acta Physica Sinica, doi: 10.7498/aps.73.20241278
[11]	Liu Ye, Niu He-Ran, Li Bing-Bing, Ma Xin-Hua, Cui Shu-Wang. Application of machine learning in cosmic ray particle identification. Acta Physica Sinica, doi: 10.7498/aps.72.20230334
[12]	Guan Xing-Yue, Huang Heng-Yan, Peng Hua-Qi, Liu Yan-Hang, Li Wen-Fei, Wang Wei. Machine learning in molecular simulations of biomolecules. Acta Physica Sinica, doi: 10.7498/aps.72.20231624
[13]	Sun Jing-Qi, Wu Xu-Cai, Que Zhi-Xiong, Zhang Wei-Bing. Prediction of ferromagnetic materials with high Curie temperature based on material composition information. Acta Physica Sinica, doi: 10.7498/aps.72.20230382
[14]	Yang Zhang-Zhang, Liu Li, Wan Zhi-Tao, Fu Jia, Fan Qun-Chao, Xie Feng, Zhang Yi, Ma Jie. Combining machine learning algorithm to improve prediction performance of ab initio method for vibrational energy spectra of HF/HBr/H³⁵Cl/Na³⁵Cl. Acta Physica Sinica, doi: 10.7498/aps.72.20221953
[15]	Zhang Yi-Fan, Ren Wei, Wang Wei-Li, Ding Shu-Jian, Li Nan, Chang Liang, Zhou Qian. Machine learning combined with solid solution strengthening model for predicting hardness of high entropy alloys. Acta Physica Sinica, doi: 10.7498/aps.72.20230646
[16]	Li Wei, Long Lian-Chun, Liu Jing-Yi, Yang Yang. Classification of magnetic ground states and prediction of magnetic moments of inorganic magnetic materials based on machine learning. Acta Physica Sinica, doi: 10.7498/aps.71.20211625
[17]	Lin Jian, Ye Meng, Zhu Jia-Wei, Li Xiao-Peng. Machine learning assisted quantum adiabatic algorithm design. Acta Physica Sinica, doi: 10.7498/aps.70.20210831
[18]	Chen Jiang-Zhi, Yang Chen-Wen, Ren Jie. Machine learning based on wave and diffusion physical systems. Acta Physica Sinica, doi: 10.7498/aps.70.20210879
[19]	Guo Shu-Hui, Lu Xin. Live streaming: Data mining and behavior analysis. Acta Physica Sinica, doi: 10.7498/aps.69.20191776
[20]	Duan Yan-Hui, Wu Wen-Hua, Fan Zhao-Lin, Luo Jia-Qi. Proper orthogonal decomposition-based data mining of aerodynamic shape for design optimization. Acta Physica Sinica, doi: 10.7498/aps.66.220203

Metrics

Abstract views: 494
PDF Downloads: 15
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板