Machine learning based on wave and diffusion physical systems

Chen Jiang-Zhi; Yang Chen-Wen; Ren Jie

doi:10.7498/aps.70.20210879

Abstract

Recently, the application of physics to machine learning and the interdisciplinary convergence of the two have attracted wide attention. This paper focuses on exploring the internal relationship between physical systems and machine learning, and also on promoting machine learning algorithm and physical implementation. We summarize the researches of machine learning in wave systems and diffusion systems, and introduce some of the latest research results. We first discuss the realization of supervised learning for wave systems, including the wave optics realization of neural networks, the wave realization of quantum search, the recurrent neural networks based on wave systems, and the nonlinear wave computation of neural morphology. Then, we discuss the machine learning algorithms inspired by diffusion systems, such as the classification algorithm based on diffusion dynamics, data mining and information filtering based on thermal diffusion, searching for optimization based on population diffusion, etc. The physical mechanism of diffusion system can inspire the construction of efficient machine learning algorithms for the classification and optimization of complex systems and physics research, which may create a new vision for the development of physics inspired algorithms and hardware implementation, and even the integration of software and hardware.

Keywords:

Authors and contacts

1.
Shanghai Key Laboratory of Special Artificial Microstructure Materials and Technology, Center for Phononics and Thermal Energy Science, School of Physics Science and Engineering, Tongji University, Shanghai 200092, China
2.
Shanghai Research Institute for Intelligent Autonomous Systems, Tongji University, Shanghai 200092, China

Corresponding author: Ren Jie, xonics@tongji.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 11935010, 11775159), the Natural Science Foundation of Shanghai Science and Technology Committee, China (Grant No. 18JC1410900), the Opening Project of Shanghai Key Laboratory of Special Artificial Microstructure Materials and Technology, China, and the Fundamental Research Funds for the Central Universities, China

FullText HTML : translate this paragraph

References

[1]	Eslami S M A, Jimenez R D, Besse F, et al. 2018 Science 360 1204 Google Scholar
[2]	Mikolov T, Karafiát M, Burget L, Černocký J, Khudanpur S 2010 11th Annual Conference of the International-Speech-Communication-Association Makuhari, Japan, September 26−30, 2010 pp1045−1048
[3]	Krizhevsky A, Sutskever I, Hinton G E 2012 Advances in Neural Information Processing Systems 25 1097
[4]	Liakos K G, Busato P, Moshou D, Pearson S, Bochtis D 2018 Sensors 18 2674 Google Scholar
[5]	Carleo G, Cirac I, Cranmer K, Daudet L, Schuld M, Tishby N, Vogt-Maranto L, Zdeborov'a L 2019 Rev. Mod. Phys. 91 045002 Google Scholar
[6]	Wetzstein G, Ozcan A, Gigan S, Fan S, Englund D, Solja J M, Denz C, Miller D, Psaltis D 2020 Nature 588 39
[7]	Miller D A 2019 Adv. Opt. Photonics 11 679 Google Scholar
[8]	Graves A, Wayne G, Reynolds M, Harley T, Danihelka I, Grabska-Barwińska A, Colmenarejo S G, Grefenstette E, Ramalho T, Agapiou J 2016 Nature 538 471 Google Scholar
[9]	Brunner D, Soriano M C, Mirasso C R, Fischer I 2013 Nat. Commun. 4 1364 Google Scholar
[10]	Mehta P, Bukov M, Wang C H, Day A G, Richardson C, Fisher C K, Schwab D 2019 Phys. Rep. 810 1 Google Scholar
[11]	Sarantoglou G, Skontranis M, Bogris A, Mesaritakis C 2020 2020 Optical Fiber Communications Conference and Exhibition (OFC) San Diego, CA, USA, March 8−12, 2020 p3
[12]	Feldmann J, Youngblood N, Wright C D, Bhaskaran H, Pernice W H P 2019 Nature 569 208 Google Scholar
[13]	Hornik K, Stinchcombe M, White H 1989 IEEE Trans. Neural Networks 2 359 Google Scholar
[14]	Hopfield J J 1982 PNAS 79 2554 Google Scholar
[15]	Farhat N, Psaltis D, Prata A, Paek E 1985 Appl. Opt. 24 10 1469
[16]	MacQueen J B 1967 Proceedings of the fifth Berkeley Symposium on Mathematical Statistics and Probability (Vol. 1) (California: University of California Press) pp281−297
[17]	Dempster A P, Laird N M, Rubin D B 1977 J. R. Stat. Soc. Ser. B-Stat. Methodol. 39 1
[18]	Jolliffe I T 1986 Principal Component Analysis (New York: Springer) pp129−155
[19]	Roweis S T, Saul L K 2000 Science 290 2323 Google Scholar
[20]	Tenenbaum J B, De Silva V, Langford J C 2000 Science 290 2319 Google Scholar
[21]	Long Y, Ren J, Chen H 2020 Phys. Rev. Lett. 124 18 185501 Google Scholar
[22]	Chung F, Yau S T 2000 J. Comb. Theory Ser. A 91 191 Google Scholar
[23]	Jiao S, Gao Y, Feng J, Lei T, Yuan X 2020 Opt. Express 28 3 3717 Google Scholar
[24]	Miller D 2013 Photonics Res. 1 1 Google Scholar
[25]	Shen Y, Harris N C, Skirlo S, Prabhu M, Baehr-Jones T, Hochberg M, Sun X, Zhao S, Larochelle H, Englund D, Soljačić M 2017 Nat. Photonics 11 441 Google Scholar
[26]	Chakraborty I, Saha G, Roy K 2019 Phys. Rev. Appl. 11 014063 Google Scholar
[27]	Chang J, Sitzmann V, Dun X, Heidrich W, Wetzstein G 2018 Sci Rep 8 12324
[28]	Zuo Y, Li B, Zhao Y, Jiang Y, Chen Y C, Chen P, Jo G B, Liu J, Du S 2019 Optica 6 1132 Google Scholar
[29]	Lin X, Rivenson Y, Yardimci N T, Veli M, Luo Y, Jarrahi M, Ozcan A 2018 Science 361 1004 Google Scholar
[30]	Qian C, Lin X, Lin X, Xu J, Sun Y, Li E, Zhang B, Chen H 2020 Light-Sci. Appl. 9 59 Google Scholar
[31]	Zhou T, Fang L, Yan T, Wu J, Li Y, Fan J, Wu H, Lin X, Dai Q 2020 Photonics Res. 8 940 Google Scholar
[32]	Dun X, Ikoma H, Wetzstein G, Wang Z, Cheng X, Peng Y F 2020 Optica 7 913 Google Scholar
[33]	Weng J, Ding Y, Hu C, Zhu X F, Liang B, Yang J, Cheng J 2020 Nat. Commun. 11 6309 Google Scholar
[34]	Yan T, Wu J, Zhou T, Xie H, Xu F, Fan J, Fang L, Lin X, Dai Q 2019 Phys. Rev. Lett. 123 2 023901 Google Scholar
[35]	Zangeneh-Nejad F, Sounas D L, Alù A, Fleury R 2021 Nat. Rev. Mater. 6 207 Google Scholar
[36]	Zuo S Y, Wei Q, Cheng Y, Liu X J 2017 Appl. Phys. Lett. 110 011904 Google Scholar
[37]	Zuo S Y, Tian Y, Wei Q, Cheng Y, Liu X J 2017 J. Appl. Phys. 123 091704 Google Scholar
[38]	Zuo S, Wei Q, Tian Y, Cheng Y, Liu X 2018 Sci Rep 8 10103 Google Scholar
[39]	Zangeneh-Nejad F, Fleury R 2018 New J. Phys. 20 073001 Google Scholar
[40]	Yang C, Liu T, Zhu J, Ren J, Chen H 2021 Phys. Rev. Appl. 15 044040 Google Scholar
[41]	Hughes T, Williamson I A D, Minkov M, Fan S 2019 Sci. Adv. 5 eaay6946 Google Scholar
[42]	Romera M, Talatchian P, Tsunegi S, Abreu Araujo F, Cros V, Bortolotti P, Trastoy J, Yakushiji K, Fukushima A, Kubota H, Yuasa S, Ernoult M, Vodenicarevic D, Hirtzlin T, Locatelli N, Querlioz D, Grollier J 2018 Nature 563 230 Google Scholar
[43]	Khoram E, Chen A, Liu D, Ying L, Wang Q, Yuan M, Yu Z 2019 Photonics Res. 7 823 Google Scholar
[44]	Zhao H 2021 Sci. China-Phys. Mech. Astron. 64 270511 Google Scholar
[45]	Ren J, Wang W X, Li B, Lai Y C 2010 Phys. Rev. Lett. 104 058701 Google Scholar
[46]	Marcucci G, Pierangeli D, Conti C 2020 Phys. Rev. Lett. 125 093901 Google Scholar
[47]	Jaeger H 2001 GMD-Report 148, German National Research Institute for Computer Science
[48]	Maass W, Natschläger T, Markram H 2002 Neural Comput 14 2531 Google Scholar
[49]	Silva N A, Ferreira T D, Guerreiro A 2021 New J. Phys. 23 023013 Google Scholar
[50]	Nadler B, Lafon S, Coifman R, Kevrekidis I 2005 Appl. Comput. Harmon. Anal. 21 113 Google Scholar
[51]	Coifman R R, Lafon S, Lee A B, Maggioni M, Nadler B, Warner F, Zucker S W 2005 Proc. Natl. Acad. Sci. U.S.A. 102 7426 Google Scholar
[52]	Rodriguez-Nieva J, Scheurer M 2018 Nat. Phys. 15 790
[53]	Scheurer M S, Slager R J 2020 Phys. Rev. Lett. 124 226401 Google Scholar
[54]	Lustig E, Yair O, Talmon R, Segev M 2020 Phys. Rev. Lett. 125 12 127401 Google Scholar
[55]	Lidiak A, Gong Z X 2020 Phys. Rev. Lett. 125 225701 Google Scholar
[56]	Che Y, Gneiting C, Liu T, Nori F 2020 Phys. Rev. B 102 134213 Google Scholar
[57]	Zhang Y, Blattner M, Yu Y 2007 Phys. Rev. Lett. 99 154301 Google Scholar
[58]	Ren J, Zhou T, Zhang Y 2008 EPL 82 58007 Google Scholar
[59]	Oganov A, Pickard C, Zhu Q, Needs R 2019 Nat. Rev. Mater. 4 331 Google Scholar
[60]	Schmidt J, Marques M, Botti S, Marques M 2019 NPJ Comput. Mater. 5 83 Google Scholar
[61]	Zhang L, Wang Y, Lü J, Ma Y 2017 Nat. Rev. Mater. 2 17005 Google Scholar
[62]	Pickard C J, Needs R J 2011 J. Phys. Condens. Matter 23 053201 Google Scholar
[63]	Eberhart R, Kennedy J MHS'95. Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, October 4–6 1995 pp39−43
[64]	Wang Y, Lü J, Zhu L, Ma Y 2010 Phys. Rev. B 82 094116 Google Scholar
[65]	Wang Y, Lü J, Zhu L, Ma Y 2012 Comput. Phys. Commun. 183 2063 Google Scholar
[66]	Wang Y, Lü J, Zhu L, Lu S, Yin K, Li Q, Wang H, Zhang L, Ma Y 2015 J. Phys. Condens. Matter 27 20 203203 Google Scholar
[67]	Wang H, Wang Y, Lü J, Li Q, Zhang L, Ma Y 2016 Comput. Mater. Sci. 112 406 Google Scholar
[68]	Tong Q, Lv J, Gao P, Wang Y 2019 Chin. Phys. B 28 106105 Google Scholar
[69]	Gao Z B, Dong X, Li N B, Ren J 2017 Nano Lett. 17 772 Google Scholar
[70]	Yan S, Wang Y, Gao Z, Long Y, Ren J 2021 Chin. Phys. Lett. 38 027301 Google Scholar
[71]	Geodecker S 2004 J. Chem. Phys. 120 9911 Google Scholar
[72]	王磊, 刘金国 2021 物理 50 69 Google Scholar Wang L, Liu J G 2021 Physics 50 69 Google Scholar
[73]	Long Y, Ren J, Li Y, Chen H 2019 Appl. Phys. Lett. 114 181105 Google Scholar
[74]	Tan Y T, Wang L Q, Wang Z, Peng J, Ren J 2021 Chin. Phys. B 30 036301 Google Scholar
[75]	Miller D 2017 J. Lightwave Technol. 35 346 Google Scholar

Cited By

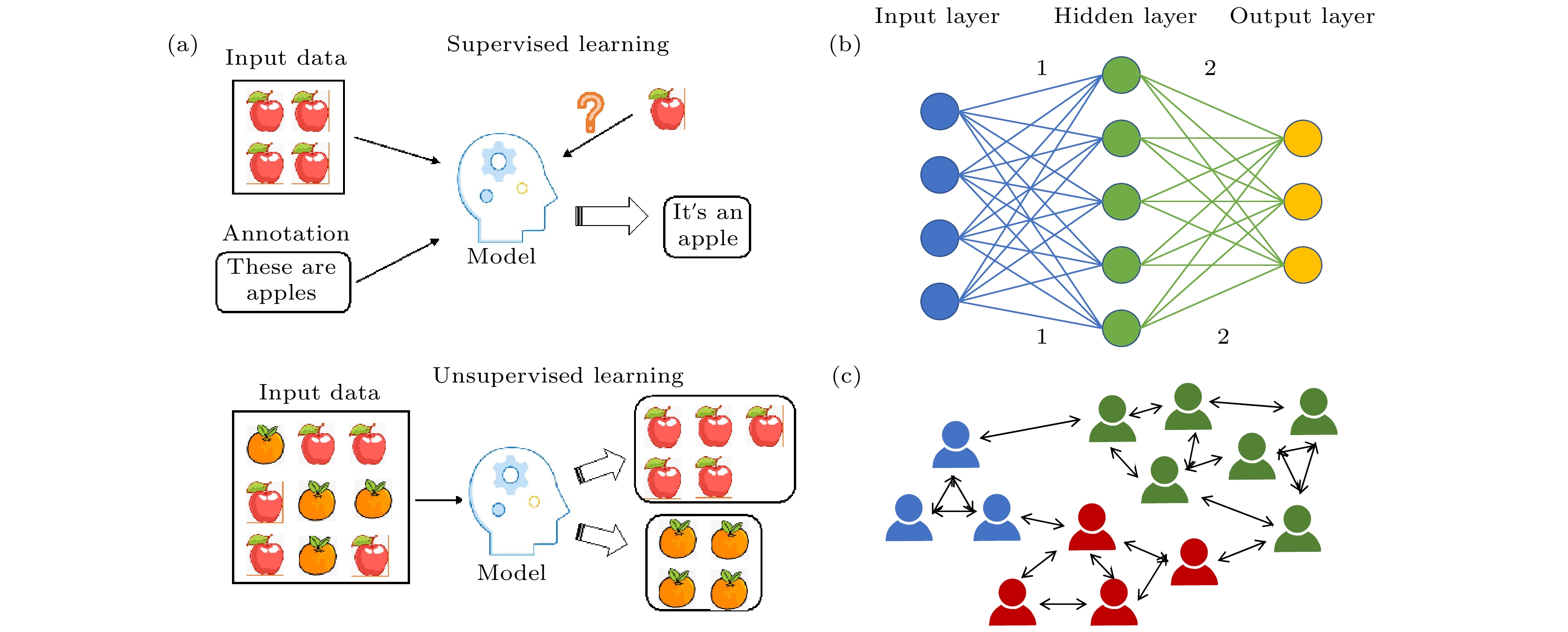
图 1 (a) 监督学习与无监督学习; (b) 一个单隐藏层神经网络的基本结构, 各层神经元根据权重系数相互连接; (c)利用无监督学习进行社交网络分析

Figure 1. (a) Supervised learning and unsupervised learning; (b) the structure of a single hidden-layer neural network, where neurons are connected by weight coefficients; (c) unsupervised learning can be applied in social network analysis.

DownLoad: Full-Size Img PowerPoint

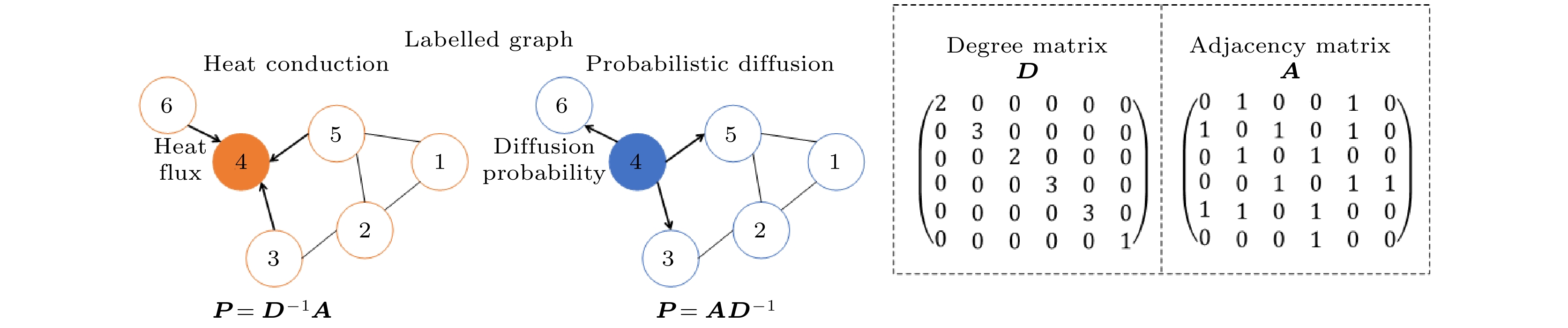
图 2 波在不同介质中的传播以及相应的线性矩阵运算　(a) 传统光学4f系统在傅里叶空间中实现乘法, 对应于在原空间中的卷积. 两个透镜分别实现傅里叶变换和傅里叶逆变换, 散射层对应于核矩阵, 场与薄散射层的相互作用相当于与对角矩阵的乘积; (b) 改进后的4f系统可以用光栅多次复制输入场, 并用不同的核矩阵进行卷积; (c) 通过类似4f的系统可以实现矢量-矩阵乘法, 实现一维行向量与稠密矩阵相乘, 得到一位列向量^[6]

Figure 2. Wave propagation through different media and the corresponding linear matrix operations: (a) A traditional optical 4f system realizes multiplication in Fourier space, which corresponds to the convolution in the original space; (b) modified 4f systems can copy the input field with a grating and use different kernels for convolution; (c) a 4f-type system can implement the vector–matrix multiplication^[6].

DownLoad: Full-Size Img PowerPoint

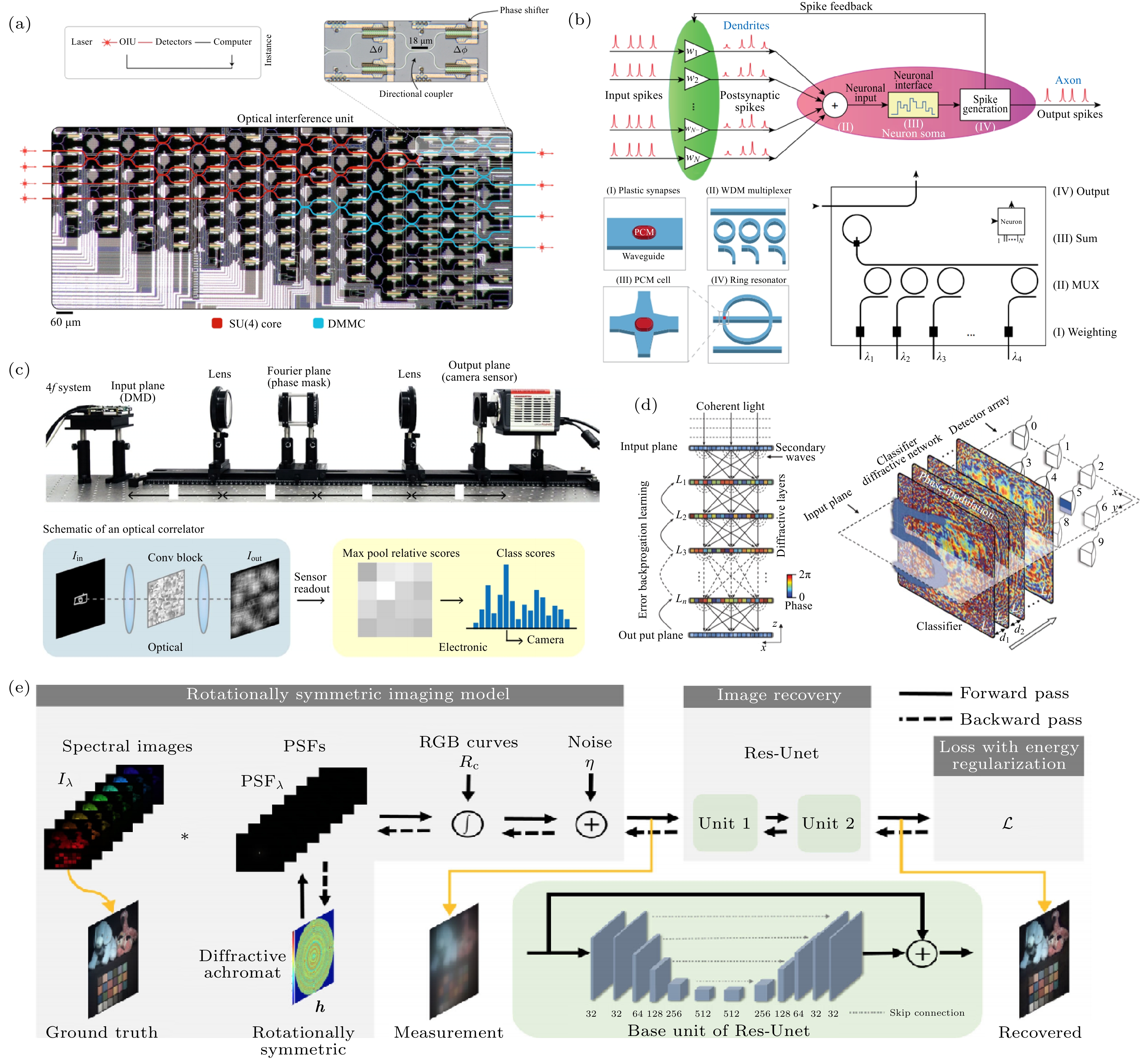
图 3 (a) 基于相干光和全光学矩阵乘法的硅光子神经形态电路可用于实现元音分类^[25]; (b) 基于波分复用(WDM)的分层结构构成的全光脉冲神经网络, 能够实现图像和语言识别^[12]; (c) 改进的光学4f系统实现卷积神经网络, 提高图像分类性能^[27]; (d) 全光衍射深度神经网络实现数字分类^[29]; (e) 光学衍射元件与图像处理算法端对端协同设计^[32]

Figure 3. (a) Nanophotonic circuits based on coherent light and all-optical matrix multiplication is capable for vowel recognition^[25]; (b) image and language recognition are achieved by an all-optical spiking neural networking with wavelength division multiplexing (WDM)^[12]; (c) a design for an optical convolutional layer using a modified optical 4f system^[27]; (d) an all-optical diffractive deep neural network that implements the digit classification^[29]; (e) end-to-end learning paradigms of diffractive optics and processing algorithms^[32].

DownLoad: Full-Size Img PowerPoint

图 4 (a) 基于声学超构神经网络的被动目标识别^[33]; (b) 利用声表面波系统实现量子搜索算法, 实现与量子逻辑门相似的操作^[40]

Figure 4. (a) Passive object recognition with acoustic meta-neural-network^[33]; (b) realize quantum search algorithm with acoustic system, achieving operations similar to quantum logic gates^[40].

DownLoad: Full-Size Img PowerPoint

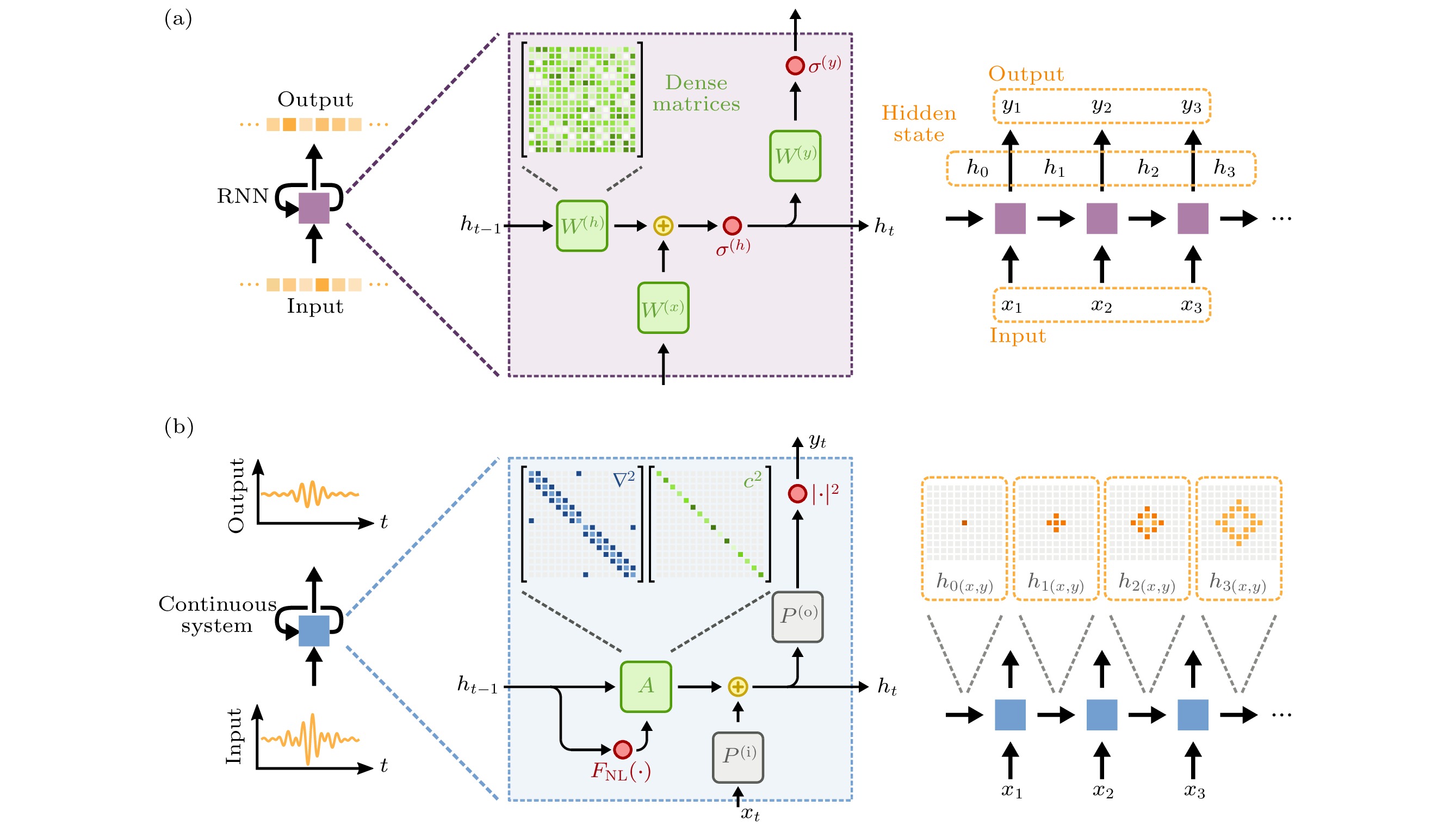
图 5 标准RNN和波物理的对比　(a)具有离散的输入、输出序列的RNN的更新过程; (b) 具有连续输入、输出序列的波动系统系统的更新过程^[41]

Figure 5. Comparison of a standard RNN and a wave system: (a) The update process of an standard RNN with discrete input and output sequence; (b) the update process of a wave-based physical system with continuous input and output sequence^[41].

DownLoad: Full-Size Img PowerPoint

图 6 神经形态的非线性波动网络　(a) 单波层前馈网络(SWFN)包含编码层、储蓄层和读出层, 其中波按照非线性偏微分方程演化; (b) 偏差$ {\psi }_{b} $的演化、波的演化以及近似计算一维函数$ y={\rm{sin}}\left({\text{π}}x\right)/\left({\text{π}}x\right) $的结果; (c) SWFN用于学习鲍鱼数据集; (d) 用孤子训练通用的布尔逻辑门^[46]

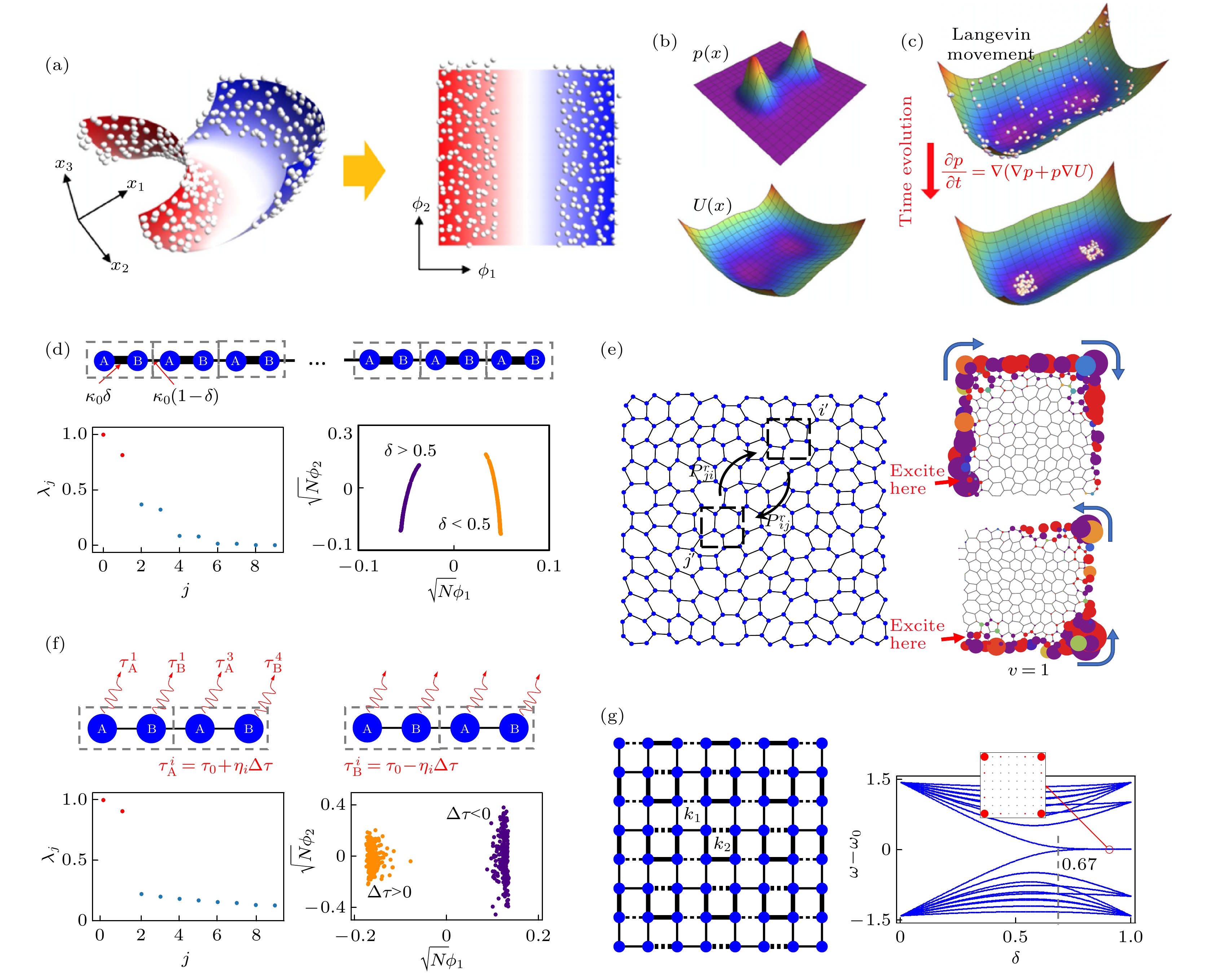
Figure 6. Neuromorphic computing by nonlinear waves: (a) Single wave-layer feed forward neural network (SWFN) with input layer, reservoir and readout layer, where the wave evolves according to a nonlinear partial differential equation; (b) the bias and wave evolution and results of learning the function $ y={\rm{sin}}\left({\text{π}}x\right)/\left({\text{π}}x\right) $; (c) results of learning the abalone dataset; (d) training a universal logic gates by soliton gases^[46].

DownLoad: Full-Size Img PowerPoint

图 7 利用扩散映射实现典型声子系统中的流形聚类　(a) 流形空间降维; (b) 流形空间的样本数据分布与势能绘景; (c) 流形空间的扩散与凝聚, 稳态显示出天然的聚类; (d)随机耦合的无序Su-Schrieffer-Heeger(SSH)声子链; (e) 无序非晶态声子的拓扑分类; (f) 一维非厄米声子链; (g) 高阶拓扑声子^[21]

Figure 7. Diffusion mapping in typical phononic systems to realize manifold clustering: (a) Dimension reduction in manifold space; (b) the probability distribution of samples and the effective landscape; (c) along with evolution, the samples diffuse and finally concentrate on positions with minimum local potentials, which indicates the clustering; (d)–(g) applications in disordered photonic SSH chain, amorphous topological phononics, 1D non-Hermitian phononic chain, high-order topological phononics^[21].

DownLoad: Full-Size Img PowerPoint

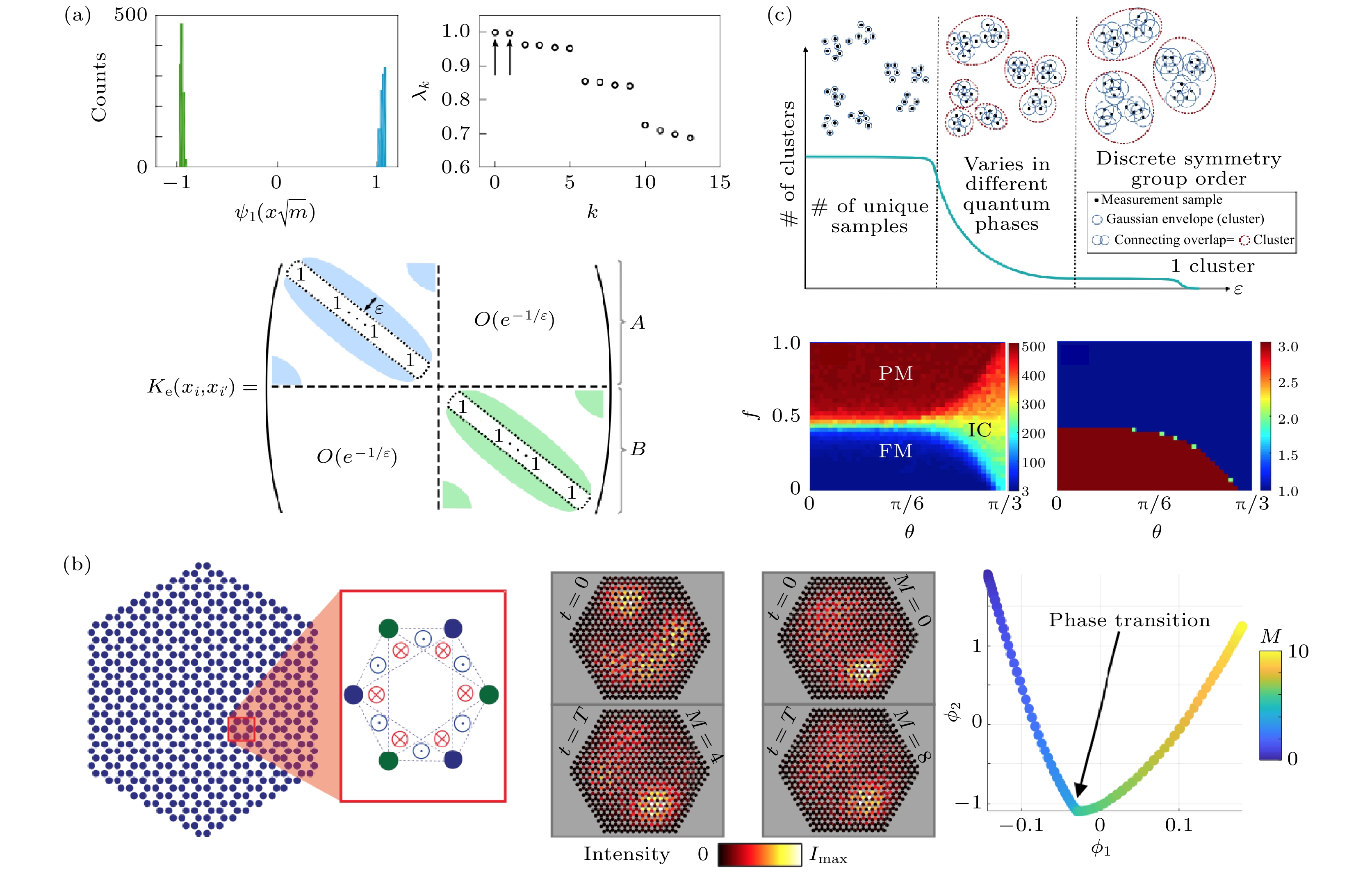
图 8 基于扩散映射的无监督学习方法适用于解决不同物理系统中的拓扑分类问题　(a) 一维XY模型拓扑序的检测^[52]; (b) 扩散映射能够不借助边缘态, 识别Haldane模型描述的拓扑相变点^[54]; (c) 量子系统中的扩散映射算法, 能够无监督地识别$ {\mathbb{Z}}_{3} $横场伊辛模型的量子相^[55]

Figure 8. The unsupervised learning with diffusion map is applied to solve topology identification in different physical systems: (a) Identifying the topological order in 1-dimensional XY model^[52]; (b) detection of the phase transition for the Haldane model without the edge states^[54]; (c) diffusion maps in learning quantum phases with a $ {\mathbb{Z}}_{3} $ transverse field Ising model^[55].

DownLoad: Full-Size Img PowerPoint

图 9 标号图表明6个点(项目)之间的连接关系, 右侧是对应的权重矩阵和邻接矩阵

Figure 9. Labelled graphs show the connection of 6 points (items), and the corresponding degree matrix and adjacency matrix are on the right side.

DownLoad: Full-Size Img PowerPoint

图 10 (a) 全局及局部粒子群优化算法示意图; (b) 粒子群优化算法中速度及位置更新示意图^[68]; (c) 多目标优化的二维SnSe材料定向设计工作流程图; (d) 室温下(300 K), 二维SnSe材料单层结构的自由能; (e) 图(d) 中第一Pareto前沿(红线)上的四种新型单层结构的三视图, 深灰色和绿色的球分别表示Sn原子和Se原子^[70]

Figure 10. (a) The diagram of PSO; (b) The schematic diagram of the velocity and position updates in PSO^[68]; (c) workflow of the multi-objective optimization for 2D SnSe materials design; (d) thermopower landscape at room temperature (300 K) versus the free energy of 2D SnSe materials; (e) four 2D SnSe structures on the first Pareto front, where the dark gray and green balls denote Sn and Se atoms, respectively^[70].

DownLoad: Full-Size Img PowerPoint

map

[1]	Eslami S M A, Jimenez R D, Besse F, et al. 2018 Science 360 1204 Google Scholar
[2]	Mikolov T, Karafiát M, Burget L, Černocký J, Khudanpur S 2010 11th Annual Conference of the International-Speech-Communication-Association Makuhari, Japan, September 26−30, 2010 pp1045−1048
[3]	Krizhevsky A, Sutskever I, Hinton G E 2012 Advances in Neural Information Processing Systems 25 1097
[4]	Liakos K G, Busato P, Moshou D, Pearson S, Bochtis D 2018 Sensors 18 2674 Google Scholar
[5]	Carleo G, Cirac I, Cranmer K, Daudet L, Schuld M, Tishby N, Vogt-Maranto L, Zdeborov'a L 2019 Rev. Mod. Phys. 91 045002 Google Scholar
[6]	Wetzstein G, Ozcan A, Gigan S, Fan S, Englund D, Solja J M, Denz C, Miller D, Psaltis D 2020 Nature 588 39
[7]	Miller D A 2019 Adv. Opt. Photonics 11 679 Google Scholar
[8]	Graves A, Wayne G, Reynolds M, Harley T, Danihelka I, Grabska-Barwińska A, Colmenarejo S G, Grefenstette E, Ramalho T, Agapiou J 2016 Nature 538 471 Google Scholar
[9]	Brunner D, Soriano M C, Mirasso C R, Fischer I 2013 Nat. Commun. 4 1364 Google Scholar
[10]	Mehta P, Bukov M, Wang C H, Day A G, Richardson C, Fisher C K, Schwab D 2019 Phys. Rep. 810 1 Google Scholar
[11]	Sarantoglou G, Skontranis M, Bogris A, Mesaritakis C 2020 2020 Optical Fiber Communications Conference and Exhibition (OFC) San Diego, CA, USA, March 8−12, 2020 p3
[12]	Feldmann J, Youngblood N, Wright C D, Bhaskaran H, Pernice W H P 2019 Nature 569 208 Google Scholar
[13]	Hornik K, Stinchcombe M, White H 1989 IEEE Trans. Neural Networks 2 359 Google Scholar
[14]	Hopfield J J 1982 PNAS 79 2554 Google Scholar
[15]	Farhat N, Psaltis D, Prata A, Paek E 1985 Appl. Opt. 24 10 1469
[16]	MacQueen J B 1967 Proceedings of the fifth Berkeley Symposium on Mathematical Statistics and Probability (Vol. 1) (California: University of California Press) pp281−297
[17]	Dempster A P, Laird N M, Rubin D B 1977 J. R. Stat. Soc. Ser. B-Stat. Methodol. 39 1
[18]	Jolliffe I T 1986 Principal Component Analysis (New York: Springer) pp129−155
[19]	Roweis S T, Saul L K 2000 Science 290 2323 Google Scholar
[20]	Tenenbaum J B, De Silva V, Langford J C 2000 Science 290 2319 Google Scholar
[21]	Long Y, Ren J, Chen H 2020 Phys. Rev. Lett. 124 18 185501 Google Scholar
[22]	Chung F, Yau S T 2000 J. Comb. Theory Ser. A 91 191 Google Scholar
[23]	Jiao S, Gao Y, Feng J, Lei T, Yuan X 2020 Opt. Express 28 3 3717 Google Scholar
[24]	Miller D 2013 Photonics Res. 1 1 Google Scholar
[25]	Shen Y, Harris N C, Skirlo S, Prabhu M, Baehr-Jones T, Hochberg M, Sun X, Zhao S, Larochelle H, Englund D, Soljačić M 2017 Nat. Photonics 11 441 Google Scholar
[26]	Chakraborty I, Saha G, Roy K 2019 Phys. Rev. Appl. 11 014063 Google Scholar
[27]	Chang J, Sitzmann V, Dun X, Heidrich W, Wetzstein G 2018 Sci Rep 8 12324
[28]	Zuo Y, Li B, Zhao Y, Jiang Y, Chen Y C, Chen P, Jo G B, Liu J, Du S 2019 Optica 6 1132 Google Scholar
[29]	Lin X, Rivenson Y, Yardimci N T, Veli M, Luo Y, Jarrahi M, Ozcan A 2018 Science 361 1004 Google Scholar
[30]	Qian C, Lin X, Lin X, Xu J, Sun Y, Li E, Zhang B, Chen H 2020 Light-Sci. Appl. 9 59 Google Scholar
[31]	Zhou T, Fang L, Yan T, Wu J, Li Y, Fan J, Wu H, Lin X, Dai Q 2020 Photonics Res. 8 940 Google Scholar
[32]	Dun X, Ikoma H, Wetzstein G, Wang Z, Cheng X, Peng Y F 2020 Optica 7 913 Google Scholar
[33]	Weng J, Ding Y, Hu C, Zhu X F, Liang B, Yang J, Cheng J 2020 Nat. Commun. 11 6309 Google Scholar
[34]	Yan T, Wu J, Zhou T, Xie H, Xu F, Fan J, Fang L, Lin X, Dai Q 2019 Phys. Rev. Lett. 123 2 023901 Google Scholar
[35]	Zangeneh-Nejad F, Sounas D L, Alù A, Fleury R 2021 Nat. Rev. Mater. 6 207 Google Scholar
[36]	Zuo S Y, Wei Q, Cheng Y, Liu X J 2017 Appl. Phys. Lett. 110 011904 Google Scholar
[37]	Zuo S Y, Tian Y, Wei Q, Cheng Y, Liu X J 2017 J. Appl. Phys. 123 091704 Google Scholar
[38]	Zuo S, Wei Q, Tian Y, Cheng Y, Liu X 2018 Sci Rep 8 10103 Google Scholar
[39]	Zangeneh-Nejad F, Fleury R 2018 New J. Phys. 20 073001 Google Scholar
[40]	Yang C, Liu T, Zhu J, Ren J, Chen H 2021 Phys. Rev. Appl. 15 044040 Google Scholar
[41]	Hughes T, Williamson I A D, Minkov M, Fan S 2019 Sci. Adv. 5 eaay6946 Google Scholar
[42]	Romera M, Talatchian P, Tsunegi S, Abreu Araujo F, Cros V, Bortolotti P, Trastoy J, Yakushiji K, Fukushima A, Kubota H, Yuasa S, Ernoult M, Vodenicarevic D, Hirtzlin T, Locatelli N, Querlioz D, Grollier J 2018 Nature 563 230 Google Scholar
[43]	Khoram E, Chen A, Liu D, Ying L, Wang Q, Yuan M, Yu Z 2019 Photonics Res. 7 823 Google Scholar
[44]	Zhao H 2021 Sci. China-Phys. Mech. Astron. 64 270511 Google Scholar
[45]	Ren J, Wang W X, Li B, Lai Y C 2010 Phys. Rev. Lett. 104 058701 Google Scholar
[46]	Marcucci G, Pierangeli D, Conti C 2020 Phys. Rev. Lett. 125 093901 Google Scholar
[47]	Jaeger H 2001 GMD-Report 148, German National Research Institute for Computer Science
[48]	Maass W, Natschläger T, Markram H 2002 Neural Comput 14 2531 Google Scholar
[49]	Silva N A, Ferreira T D, Guerreiro A 2021 New J. Phys. 23 023013 Google Scholar
[50]	Nadler B, Lafon S, Coifman R, Kevrekidis I 2005 Appl. Comput. Harmon. Anal. 21 113 Google Scholar
[51]	Coifman R R, Lafon S, Lee A B, Maggioni M, Nadler B, Warner F, Zucker S W 2005 Proc. Natl. Acad. Sci. U.S.A. 102 7426 Google Scholar
[52]	Rodriguez-Nieva J, Scheurer M 2018 Nat. Phys. 15 790
[53]	Scheurer M S, Slager R J 2020 Phys. Rev. Lett. 124 226401 Google Scholar
[54]	Lustig E, Yair O, Talmon R, Segev M 2020 Phys. Rev. Lett. 125 12 127401 Google Scholar
[55]	Lidiak A, Gong Z X 2020 Phys. Rev. Lett. 125 225701 Google Scholar
[56]	Che Y, Gneiting C, Liu T, Nori F 2020 Phys. Rev. B 102 134213 Google Scholar
[57]	Zhang Y, Blattner M, Yu Y 2007 Phys. Rev. Lett. 99 154301 Google Scholar
[58]	Ren J, Zhou T, Zhang Y 2008 EPL 82 58007 Google Scholar
[59]	Oganov A, Pickard C, Zhu Q, Needs R 2019 Nat. Rev. Mater. 4 331 Google Scholar
[60]	Schmidt J, Marques M, Botti S, Marques M 2019 NPJ Comput. Mater. 5 83 Google Scholar
[61]	Zhang L, Wang Y, Lü J, Ma Y 2017 Nat. Rev. Mater. 2 17005 Google Scholar
[62]	Pickard C J, Needs R J 2011 J. Phys. Condens. Matter 23 053201 Google Scholar
[63]	Eberhart R, Kennedy J MHS'95. Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, October 4–6 1995 pp39−43
[64]	Wang Y, Lü J, Zhu L, Ma Y 2010 Phys. Rev. B 82 094116 Google Scholar
[65]	Wang Y, Lü J, Zhu L, Ma Y 2012 Comput. Phys. Commun. 183 2063 Google Scholar
[66]	Wang Y, Lü J, Zhu L, Lu S, Yin K, Li Q, Wang H, Zhang L, Ma Y 2015 J. Phys. Condens. Matter 27 20 203203 Google Scholar
[67]	Wang H, Wang Y, Lü J, Li Q, Zhang L, Ma Y 2016 Comput. Mater. Sci. 112 406 Google Scholar
[68]	Tong Q, Lv J, Gao P, Wang Y 2019 Chin. Phys. B 28 106105 Google Scholar
[69]	Gao Z B, Dong X, Li N B, Ren J 2017 Nano Lett. 17 772 Google Scholar
[70]	Yan S, Wang Y, Gao Z, Long Y, Ren J 2021 Chin. Phys. Lett. 38 027301 Google Scholar
[71]	Geodecker S 2004 J. Chem. Phys. 120 9911 Google Scholar
[72]	王磊, 刘金国 2021 物理 50 69 Google Scholar Wang L, Liu J G 2021 Physics 50 69 Google Scholar
[73]	Long Y, Ren J, Li Y, Chen H 2019 Appl. Phys. Lett. 114 181105 Google Scholar
[74]	Tan Y T, Wang L Q, Wang Z, Peng J, Ren J 2021 Chin. Phys. B 30 036301 Google Scholar
[75]	Miller D 2017 J. Lightwave Technol. 35 346 Google Scholar

[1]	Deng Xiang-Wen, Wu Li-Yuan, Zhao Rui, Wang Jia-Ou, Zhao Li-Na. Application and prospect of machine learning in photoelectron spectroscopy. Acta Physica Sinica, 2024, 73(21): 210701. doi: 10.7498/aps.73.20240957
[2]	Song Rui, Liu Xue-Mei, Wang Hai-Bin, Lü Hao, Song Xiao-Yan. Hardness prediction of WC-Co cemented carbide based on machine learning model. Acta Physica Sinica, 2024, 73(12): 126201. doi: 10.7498/aps.73.20240284
[3]	Zhang Qiao, Tan Wei, Ning Yong-Qi, Nie Guo-Zheng, Cai Meng-qiu, Wang Jun-Nian, Zhu Hui-Ping, Zhao Yu-Qing. Prediction of Magnetic Janus Materials Based on Machine Learning and First-Principles Calculations. Acta Physica Sinica, 2024, 73(23): 230201. doi: 10.7498/aps.73.20241278
[4]	Zhang Xu, Ding Jin-Min, Hou Chen-Yang, Zhao Yi-Ming, Liu Hong-Wei, Liang Sheng. Machine learning based laser homogenization method. Acta Physica Sinica, 2024, 73(16): 164205. doi: 10.7498/aps.73.20240747
[5]	Zhang Jia-Hui. Machine learning for in silico protein research. Acta Physica Sinica, 2024, 73(6): 069301. doi: 10.7498/aps.73.20231618
[6]	Ouyang Xin-Jian, Zhang Yan-Xing, Wang Zhi-Long, Zhang Feng, Chen Wei-Jia, Zhuang Yuan, Jie Xiao, Liu Lai-Jun, Wang Da-Wei. Modeling ferroelectric phase transitions with graph convolutional neural networks. Acta Physica Sinica, 2024, 73(8): 086301. doi: 10.7498/aps.73.20240156
[7]	Zhang Yi-Fan, Ren Wei, Wang Wei-Li, Ding Shu-Jian, Li Nan, Chang Liang, Zhou Qian. Machine learning combined with solid solution strengthening model for predicting hardness of high entropy alloys. Acta Physica Sinica, 2023, 72(18): 180701. doi: 10.7498/aps.72.20230646
[8]	Guo Wei-Chen, Ai Bao-Quan, He Liang. Reveal flocking phase transition of self-propelled active particles by machine learning regression uncertainty. Acta Physica Sinica, 2023, 72(20): 200701. doi: 10.7498/aps.72.20230896
[9]	Liu Ye, Niu He-Ran, Li Bing-Bing, Ma Xin-Hua, Cui Shu-Wang. Application of machine learning in cosmic ray particle identification. Acta Physica Sinica, 2023, 72(14): 140202. doi: 10.7498/aps.72.20230334
[10]	Guan Xing-Yue, Huang Heng-Yan, Peng Hua-Qi, Liu Yan-Hang, Li Wen-Fei, Wang Wei. Machine learning in molecular simulations of biomolecules. Acta Physica Sinica, 2023, 72(24): 248708. doi: 10.7498/aps.72.20231624
[11]	Ai Fei, Liu Zhi-Bing, Zhang Yuan-Tao. Numerical study of discharge characteristics of atmospheric dielectric barrier discharges by integrating machine learning. Acta Physica Sinica, 2022, 71(24): 245201. doi: 10.7498/aps.71.20221555
[12]	Li Wei, Long Lian-Chun, Liu Jing-Yi, Yang Yang. Classification of magnetic ground states and prediction of magnetic moments of inorganic magnetic materials based on machine learning. Acta Physica Sinica, 2022, 71(6): 060202. doi: 10.7498/aps.71.20211625
[13]	Kang Jun-Feng, Feng Song-Jiang, Zou Qian, Li Yan-Jie, Ding Rui-Qiang, Zhong Quan-Jia. Machine learning based method of correcting nonlinear local Lyapunov vectors ensemble forecasting. Acta Physica Sinica, 2022, 71(8): 080503. doi: 10.7498/aps.71.20212260
[14]	Zhang Jia-Wei, Yao Hong-Bo, Zhang Yuan-Zheng, Jiang Wei-Bo, Wu Yong-Hui, Zhang Ya-Ju, Ao Tian-Yong, Zheng Hai-Wu. Self-powered sensing based on triboelectric nanogenerator through machine learning and its application. Acta Physica Sinica, 2022, 71(7): 078702. doi: 10.7498/aps.71.20211632
[15]	Li Ce, Yang Dong-Liang, Sun Lin-Feng. Research progress of neuromorphic devices based on two-dimensional layered materials. Acta Physica Sinica, 2022, 71(21): 218504. doi: 10.7498/aps.71.20221424
[16]	Lin Jian, Ye Meng, Zhu Jia-Wei, Li Xiao-Peng. Machine learning assisted quantum adiabatic algorithm design. Acta Physica Sinica, 2021, 70(14): 140306. doi: 10.7498/aps.70.20210831
[17]	Yang Zi-Xin, Gao Zhang-Ran, Sun Xiao-Fan, Cai Hong-Ling, Zhang Feng-Ming, Wu Xiao-Shan. High critical transition temperature of lead-based perovskite ferroelectric crystals: A machine learning study. Acta Physica Sinica, 2019, 68(21): 210502. doi: 10.7498/aps.68.20190942
[18]	Yuan Lin, Yang Xue-Song, Wang Bing-Zhong. Prediction of time reversal channel with neural network optimized by empirical knowledge based genetic algorithm. Acta Physica Sinica, 2019, 68(17): 170503. doi: 10.7498/aps.68.20190327
[19]	Peng Xiang-Kai, Ji Jing-Wei, Li Lin, Ren Wei, Xiang Jing-Feng, Liu Kang-Kang, Cheng He-Nan, Zhang Zhen, Qu Qiu-Zhi, Li Tang, Liu Liang, Lü De-Sheng. Online learning method based on artificial neural network to optimize magnetic shielding characteristic parameters. Acta Physica Sinica, 2019, 68(13): 130701. doi: 10.7498/aps.68.20190234
[20]	Zhao Yong-Ping, Wang Kang-Kang. Chaotic time series prediction using add-delete mechanism based regularized extreme learning machine. Acta Physica Sinica, 2013, 62(24): 240509. doi: 10.7498/aps.62.240509

Catalog

Vol. 70, Issue 14 - 2021-07-20

Metrics

Abstract views: 7907
PDF Downloads: 449
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板