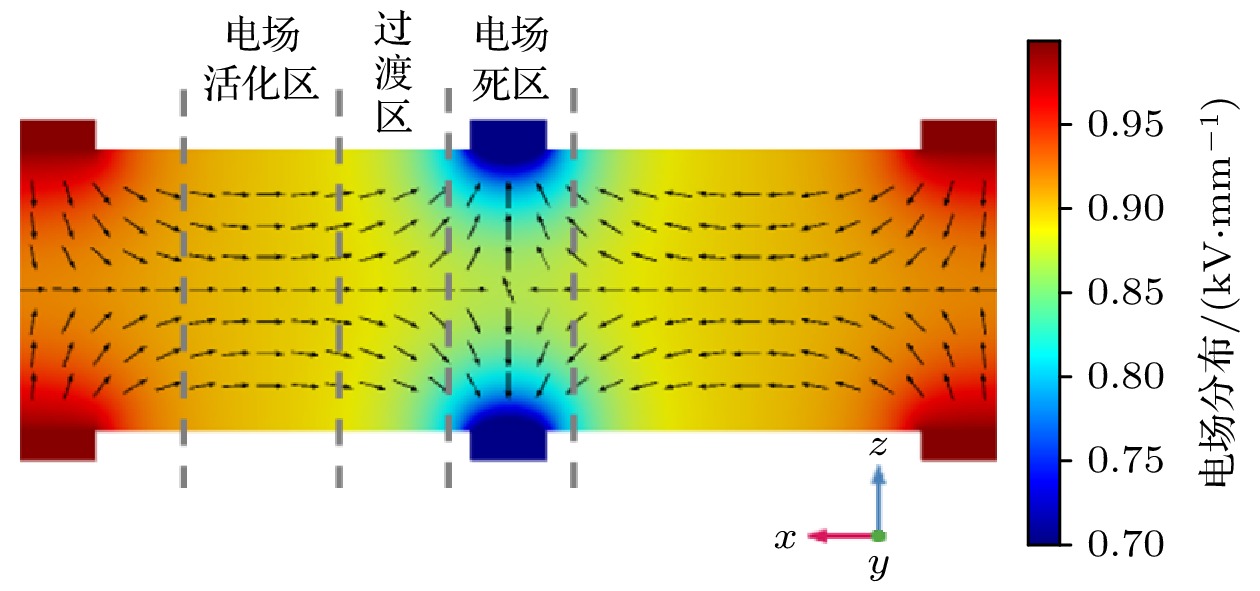
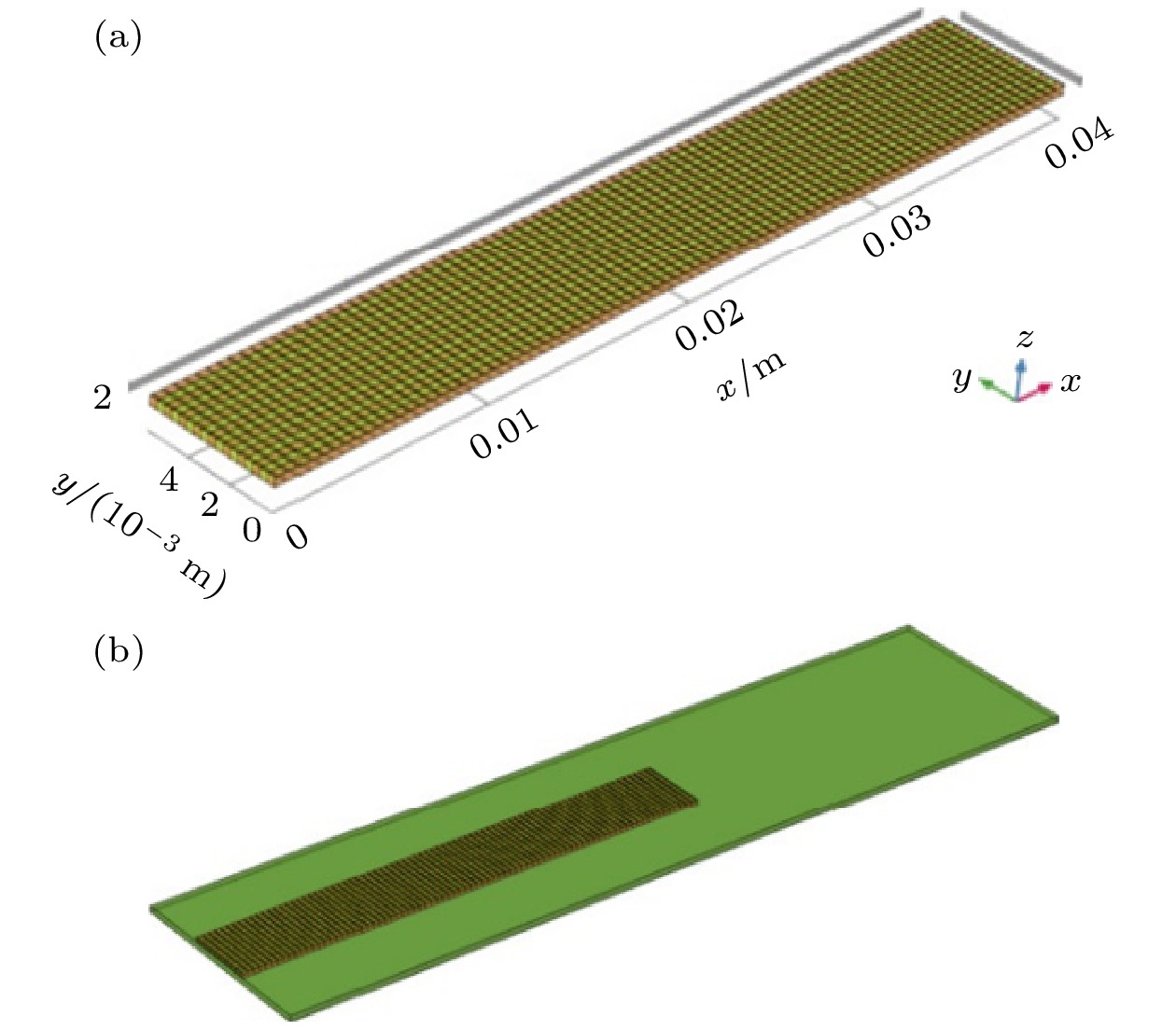
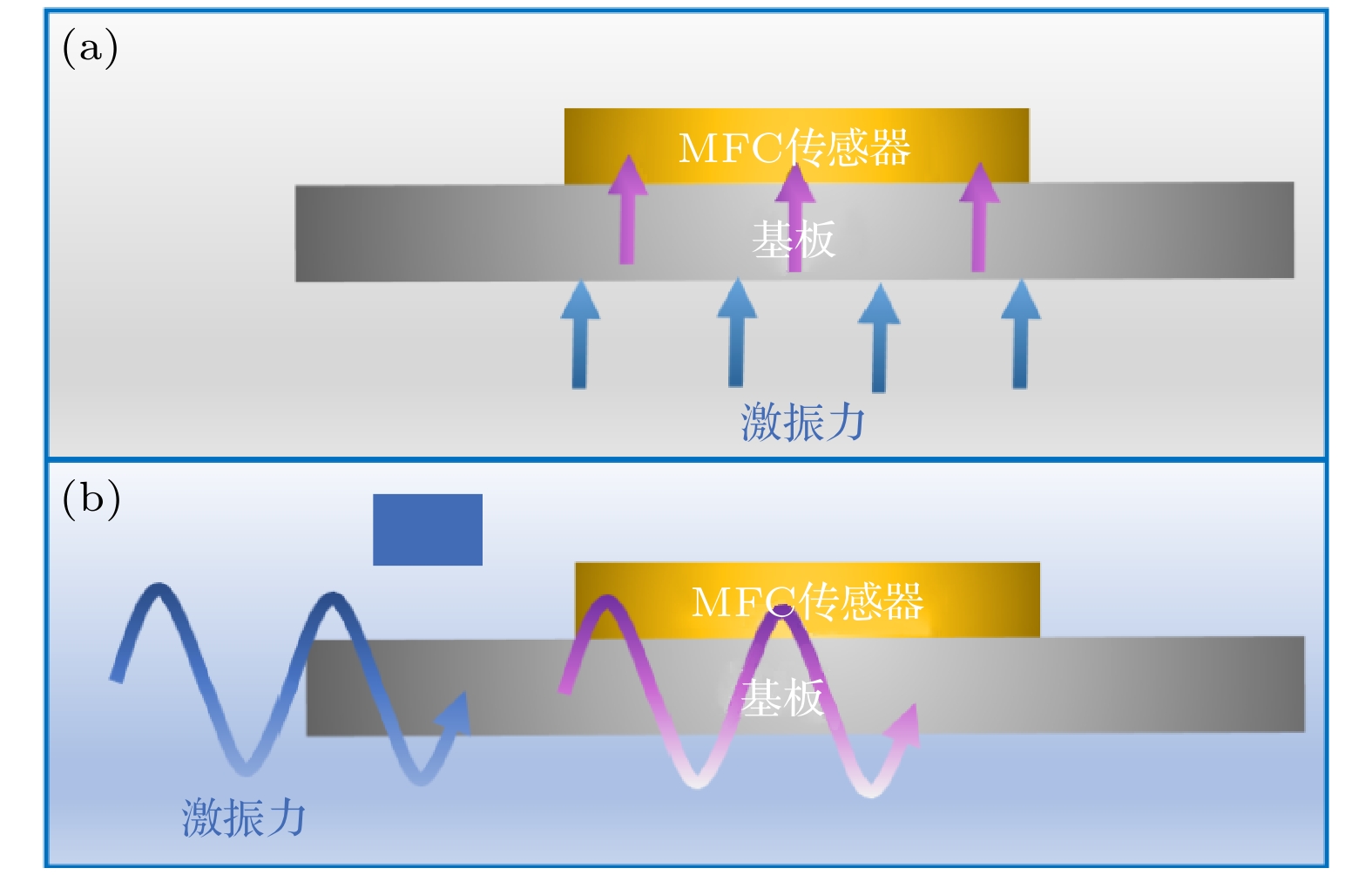
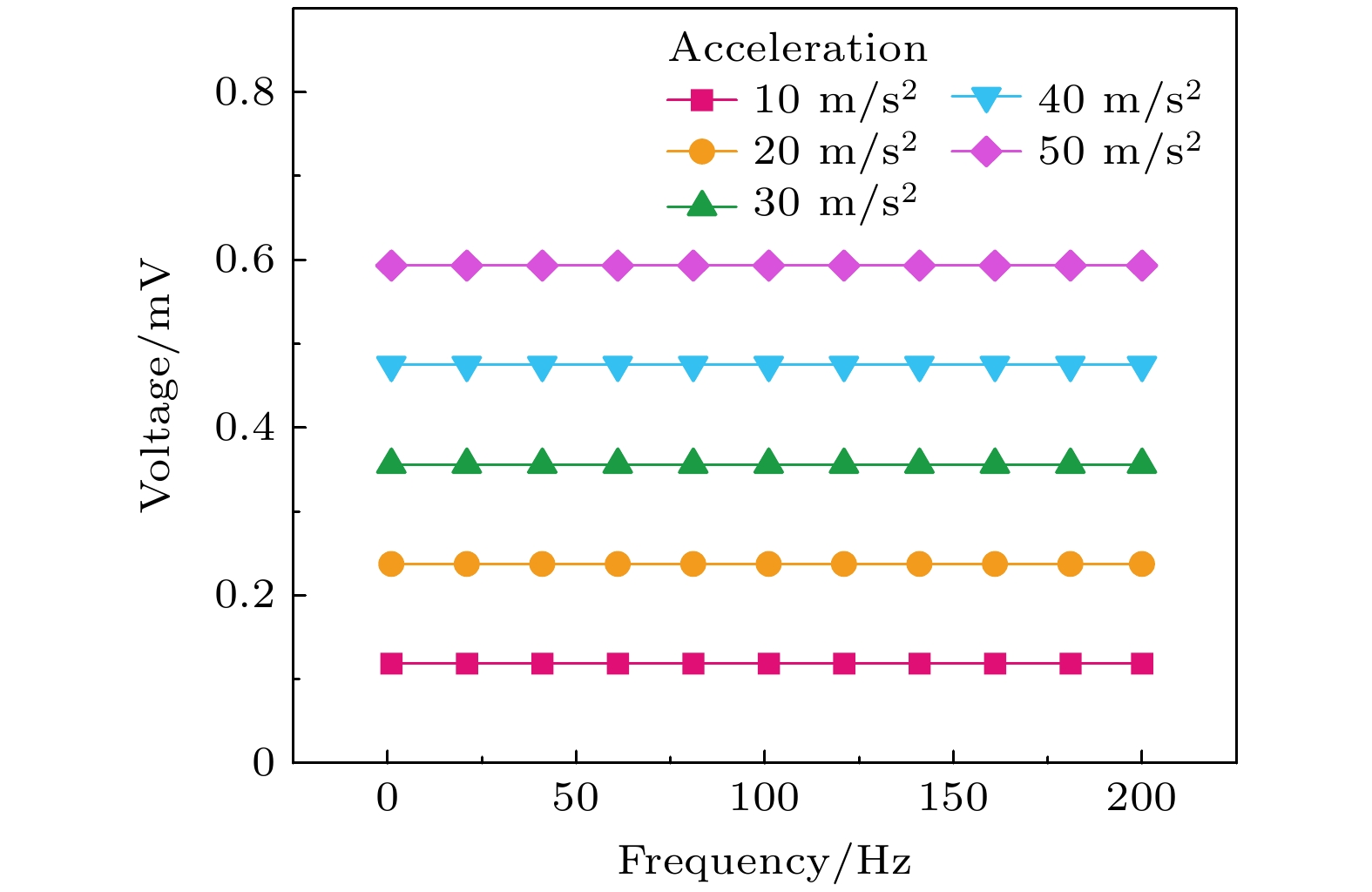
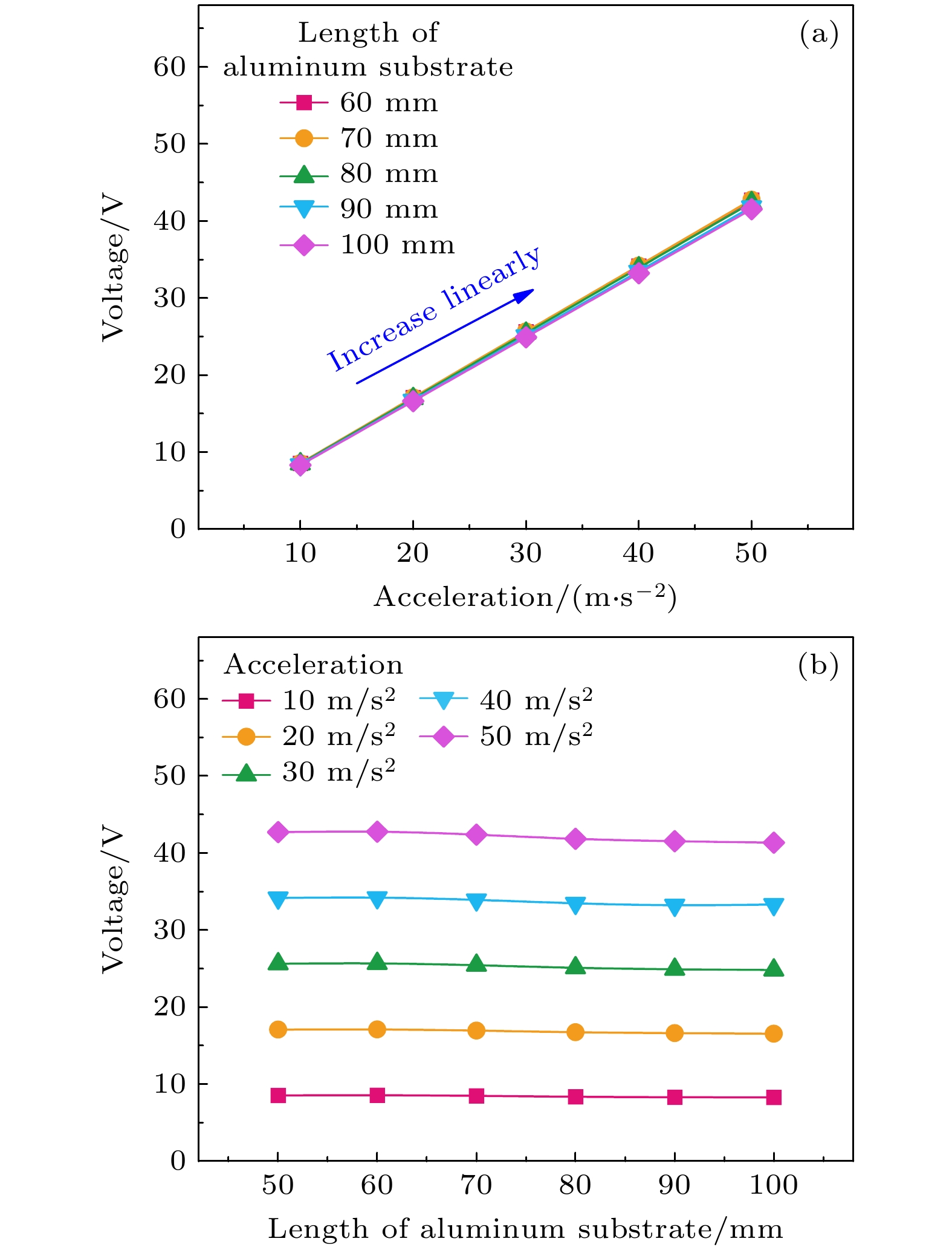
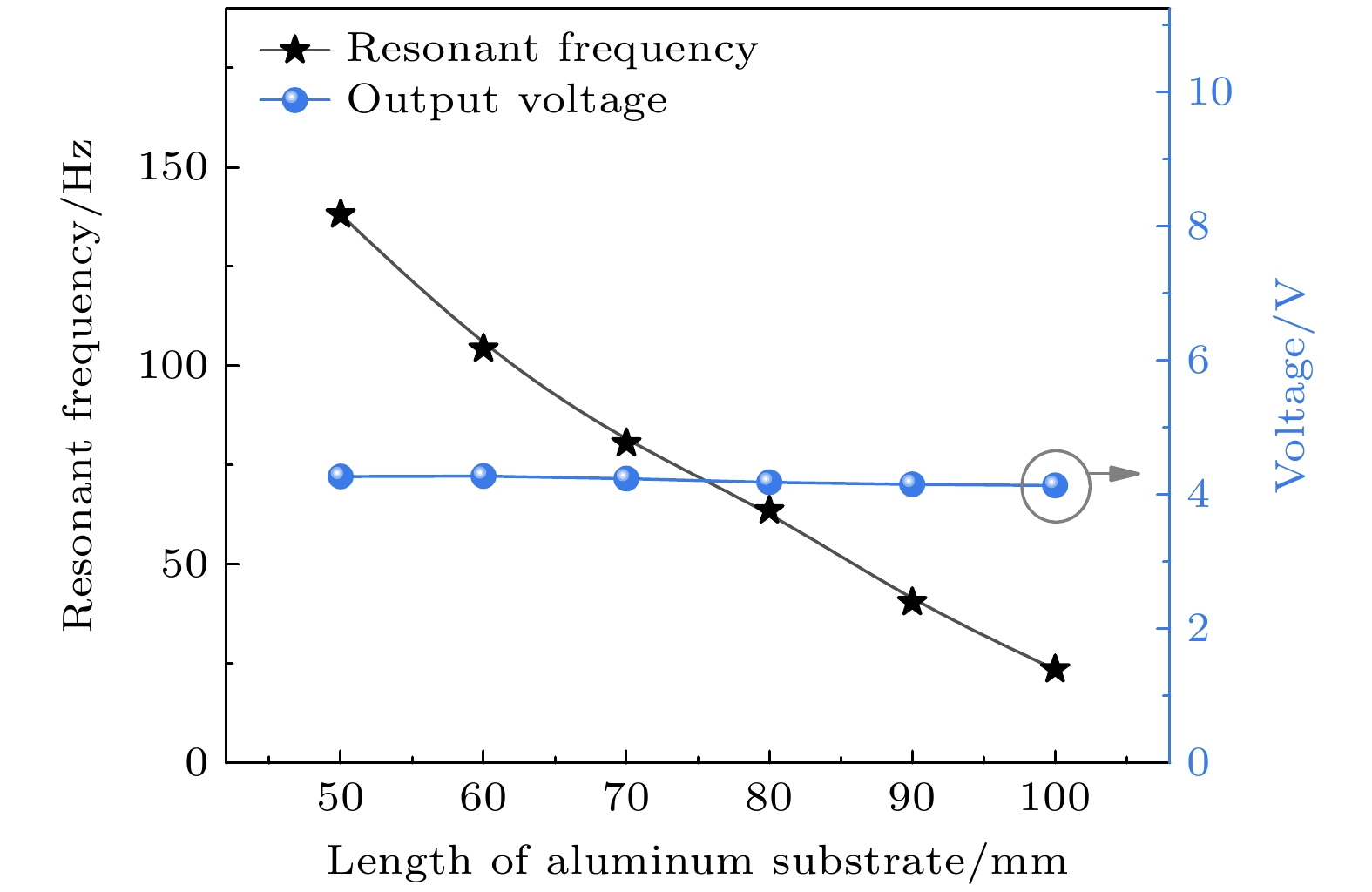
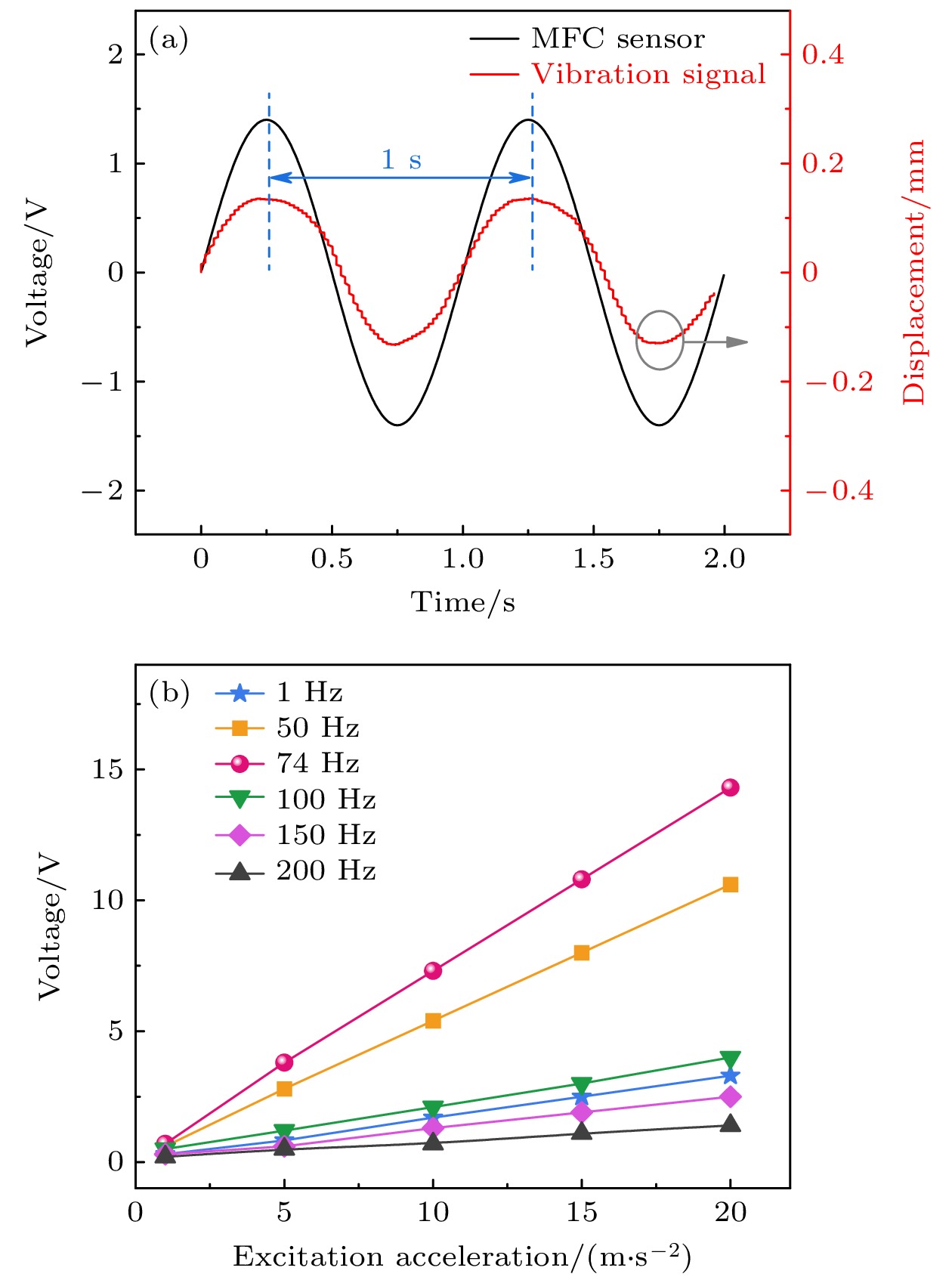
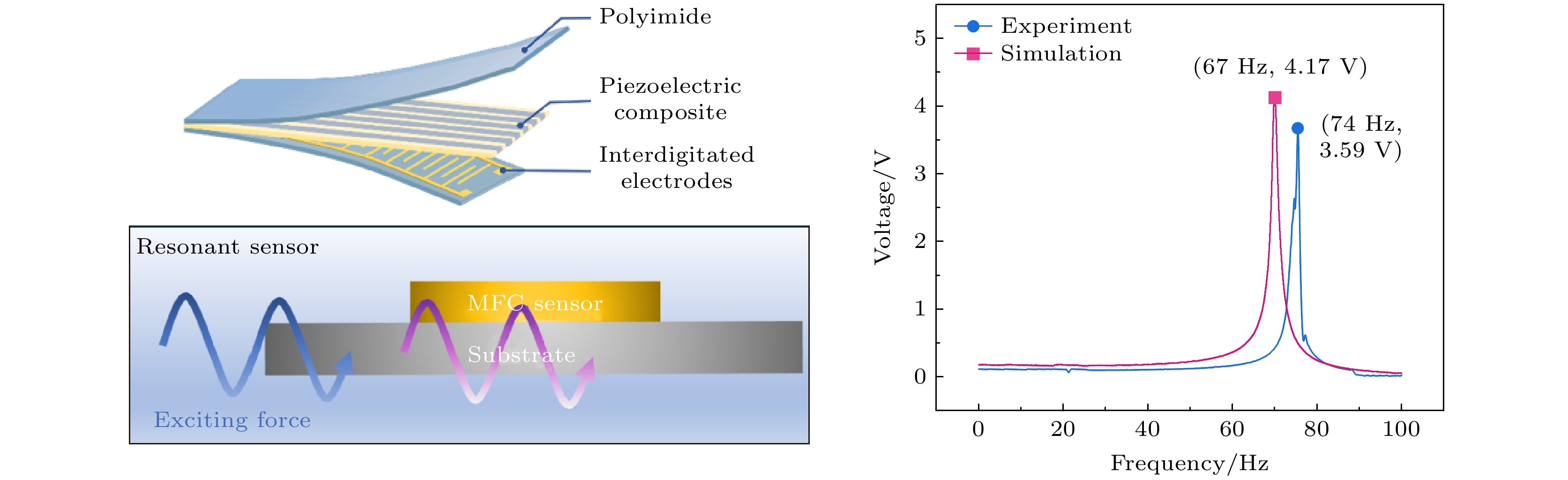
-
压电纤维复合材料(macro fiber composite, MFC)具有高压电性、高柔韧性和低损耗等优点, 被广泛应用于航空、航天、民用和军事等领域. 然而, 目前MFC传感器的研究主要聚焦于材料应用, 对于MFC传感器件仿真建模还缺乏系统性的研究. 本工作分别建立了代表性体积元模型、直接模型和混合模型, 从细节到整体、从微观到宏观对MFC的有限元模型进行了建模和分析. 一方面通过等效体积元模型, 掌握MFC内部的电场分布规律, 为力-电耦合提供理论依据; 另一方面通过直接模型和混合模型, 对MFC的实体结构进行整体建模和边界条件的加载, 为MFC贴片式传感和共振式传感的分析提供理论依据, 有效预测了MFC智能元件传感器的传感性能. 仿真结果表明, 共振式传感器性能远优于贴片式传感器, 当激振加速度为5 m/s2、悬臂梁基板长度为80 mm时, 计算得到的MFC共振式传感器的谐振频率为67 Hz, 输出电压为4.17 V. 实验结果表明, MFC传感器测试的谐振频率为74 Hz, 输出电压为3.59 V, 仿真计算结果与MFC传感器预测结果基本符合. 此外, MFC传感器在低频工作时具有优异的传感灵敏度, 传感灵敏度为7.35 V/g. 可见, MFC在低频共振时具有优异的传感特性, 构建的3种有限元模型可以有效预测MFC传感器的传感性能, 为MFC传感器的性能预测提供了保障.
-
关键词:
- 压电纤维复合材料(MFC) /
- 传感器 /
- 性能预测 /
- 有限元模型
Macro fiber composite (MFC) is extensively utilized in aviation, aerospace, civilian, and military domains due to its high piezoelectricity, flexibility, and minimal loss. Nevertheless, existing research on MFC sensors has focused on material applications, with a conspicuous lack of systematic investigation into the simulation and modeling of MFC sensor devices. In this study, three models, namely, a representative volume element (RVE) model, a direct model, and a Hybrid model are established to analyze the finite element models of MFC, covering the scales from micro to macro. On the one hand, the equivalent RVE model contributes to an understanding of the internal electric field distribution in MFC, thereby establishing a theoretical foundation for force-electric coupling. On the other hand, the application of the direct model and hybrid model accords with the boundary conditions in MFC applications, which lays a theoretical foundation for the stress sensing and resonance sensing mechanisms of MFC. These models constitute effective tools for predicting the sensing performance of MFC smart element sensors. The simulation outcomes indicate that resonant sensors exhibit significantly superior performance compared with patch sensors. Under the conditions where the excitation acceleration is 5 m/s² and the cantilever substrate length is 80 mm, the simulated resonant frequency of the MFC resonant sensor is 67 Hz, with an output voltage of 4.17 V. Experimental results confirm these findings. It is reported that the resonant frequency is 74 Hz and the output voltage is 3.59 V for the MFC sensor. The remarkable consistency between the simulation results and experimental data of the MFC sensor deserves to be emphasized. In addition, the MFC sensor shows excellent sensing sensitivity at low frequencies, with a sensitivity of 7.35 V/g. Obviously, MFC shows remarkable sensing characteristics at low-frequency resonance. The three finite element models established in this work can well predict the sensing performance of MFC sensors, thus ensuring reliable prediction of the performance of such sensors.
-
图 1 (a)宏压电纤维复合材料结构; (b)压电纤维复合材料工作模式
Fig. 1. (a) Macro fiber composite structure; (b) working mode of macro fiber composite.
图 3 MFC的代表性体积元建模 (a) RVE模型; (b) RVE模型的尺寸参数
Fig. 3. Representative volume element modeling of MFC: (a) RVE modeling diagram; (b) dimension parameter of RVE.
图 5 (a) MFC的直接模型; (b) MFC的混合模型
Fig. 5. (a) Direct model of MFC; (b) mixed model of MFC.
图 6 MFC传感器 (a)贴片式传感器; (b)共振式传感器
Fig. 6. MFC sensor: (a) MFC patch sensor; (b) MFC resonance sensor.
图 8 MFC共振传感器的传感性能 (a)加速度载荷对输出电压的影响; (b)基板长度对输出电压的影响
Fig. 8. Sensing performance of MFC resonant sensor: (a) Influence of acceleration load on output voltage; (b) influence of substrate length on output voltage.
图 10 PZT-5H基MFC传感器性能 (a)频率响应; (b)加速度响应
Fig. 10. Performance of the PZT-5H-based MFC sensor: (a) Frequency response; (b) acceleration response.
图 11 MFC传感器仿真与实验结果对比
Fig. 11. Comparison of simulation and experiment results of MFC sensor.
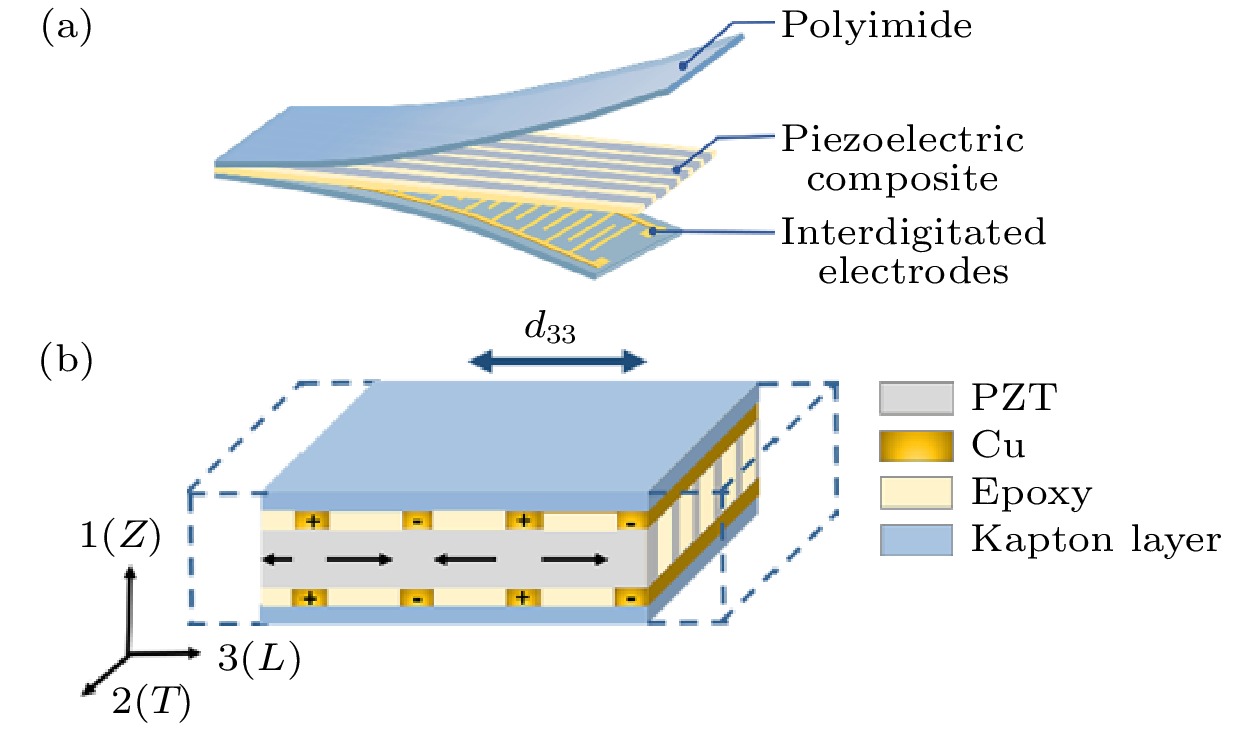
表 1 MFC代表性体积元模型尺寸参数
Table 1. Dimension parameter of RVE of MFC.
建模参数 纤维宽度 纤维高度 环氧
宽度环氧
高度电极宽度 电极高度 电极间距 纤维电极间距 定义符号 Wf Hf We He Wi Hi Si Sf 初始值/mm 0.35 0.45 0.3 0.45 0.1 0.04 0.5 0.04 
下载: 导出CSV
表 2 压电陶瓷的材料参数
Table 2. Material parameters of piezoelectric ceramic.
密度/(kg·m–3) 压电常数/(10–12C·N–1) 介电常数 柔度矩阵/(10–12m2·N–1) ρ d33 d31 d15 $\varepsilon_{11 }$ $\varepsilon_{33} $ s11 s12 s13 s33 s44 s66 7750 593 –274 741 3130 3400 16.5 –4.8 –8.5 20.7 43.5 42.6
下载: 导出CSV
表 3 环氧树脂和叉指电极的材料参数
Table 3. Material parameters of epoxy resin and interdigital electrode.
材料 密度/
(kg·m–3)弹性模量/GPa 泊松比 相对介电
常数铜电极 8960 120 0.34 — 环氧树脂 1960 1 0.38 4
下载: 导出CSV
表 4 MFC传感器性能参数
Table 4. Performance parameters of MFC sensor.
性能参数 单位 数值范围 灵敏度(±5%) V/g 0.5—7.35 工作频段(±5%) Hz 1—200 谐振频率 Hz 74 响应时间 ms <1 输出电压 V 0.5—20
下载: 导出CSV
-
[1] Hagood N W, Bent A A 1993 34th Structures, Structural Dynamics and Materials Conference La Jolla, CA, U. S. A, April 19—22, 1993
[2] Aaron A B, Nesbitt W H 1997 J. Intell. Mater. Syst. Struct. 8 903
Google Scholar
[3] Bent A A, Hagood N W, Rodgers J P 1995 J. Intell. Mater. Syst. Struct. 6 338
Google Scholar
[4] Wilkie W K, Bryant R G, High J W, Fox R L, Hellbaum R F 2000 Industrial and Commercial Applications of Smart Structures Technologies Newport Beach, USA, March 7-9, 2000
[5] Tu J W, Zhang J R, Li Z, Gao K, Liu M Y 2020 Smart Mater. Struct. 29 015038
Google Scholar
[6] Lou J Q, Chen T H, Yang Y L, Xu C, Chen H, Ma J, Cui Y G, Li G 2022 J. Vib. Control 28 290
Google Scholar
[7] Lou J Q, Gu T, Chen T H, Yang Y L, Xu C, Wei Y D, Cui Y G 2022 Mech. Syst. Signal Process. 170 108824
Google Scholar
[8] Zhou J J, Zhou J, Chen W, Tian J, Shen J, Zhang P C 2022 Compos. Struct. 299 116019
Google Scholar
[9] Wang X Y, Yuan X, Wu M L, Gao F, Yan X M, Zhou K C, Zhang D 2019 Sensors 19 1809
Google Scholar
[10] Yan M Y, Yuan X, Zhang Y, Zhang S F, Wang X Y, Gao F, Zhou K C, Zhang D 2019 Smart Mater. Struct. 28 125015
Google Scholar
[11] Yuan X, Wang X Y, Yan M Y, Gao F, Zhang S F, Zhou K C, Ji X B, Zhang D 2020 Measurement 154 107500
Google Scholar
[12] Zhou J J, Zhou J, Yu Y Y, Shen J, Zhang P C, Chen W 2023 Ceram. Intl. 49 32528
Google Scholar
[13] Huang R, Zhou J J, Shen J, Tian J, Zhou J, Chen W 2024 Materials 17 3033
Google Scholar
[14] Discalea F L, Matt H, Bartoli I, Stefano C, Gyuhae P, Charles F 2006 J. Intell. Mater. Syst. Struct. 18 373
[15] Konka H P, Wahaba M A, Lian K 2013 Sens. Actuators A 194 84
Google Scholar
[16] Pearson M R, Eaton M J, Featherston C A, Holford K M, Pullin R 2011 J. Phys. : Conf. Ser. 305 12049
Google Scholar
[17] Grzybek D, Micek P 2017 Sens. Actuators A 267 417
Google Scholar
[18] Micek P, Grzybek D 2019 Sens. Actuators A 301 111744
[19] El Najjar J, Mustapha S 2020 J. Civ. Struct. Health Monit. 10 793
Google Scholar
[20] Glouia Y, Chaabouni Y, El Oudiani A, Maatoug I, Msahli S 2019 Intl. J. Adv. Manuf. Tech. 103 4671
Google Scholar
[21] Malekimoghadam R, Icardi U 2019 Composites Part B 177 107405
Google Scholar
[22] Marino M, Wriggers P 2019 Comput. Methods Appl. Mech. Eng. 344 938
Google Scholar
[23] Yu S, Zhang D T, Qian K 2019 Appl. Composite Mater. 26 65
Google Scholar
[24] Zahid M, Sharma R, Bhagat A R, Abbas S, Kumar A, Mahajan P 2019 Composite Struct. 226 111221
Google Scholar
下载:
计量
- 文章访问数: 479
- PDF下载量: 8
- 被引次数: 0
