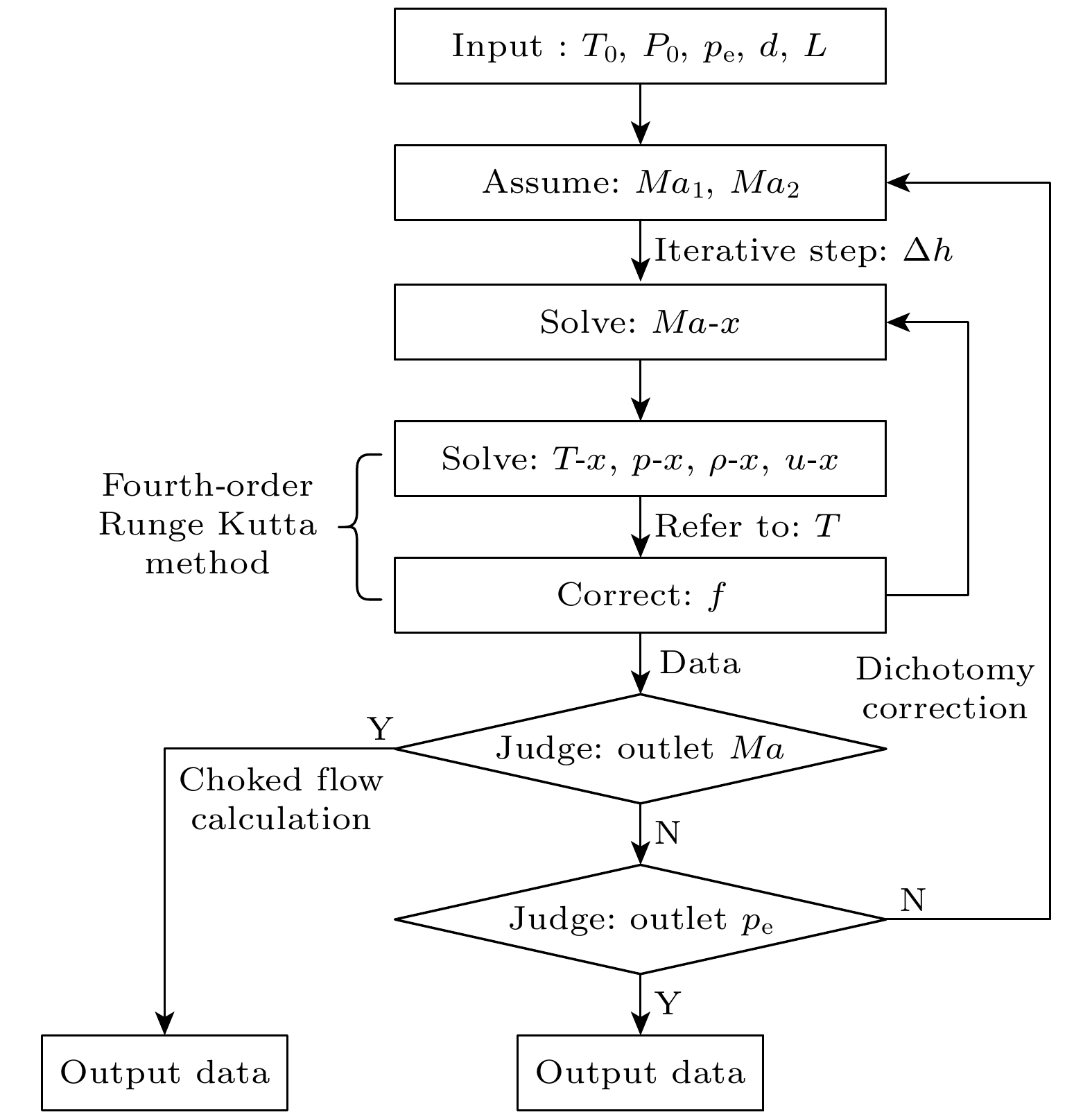
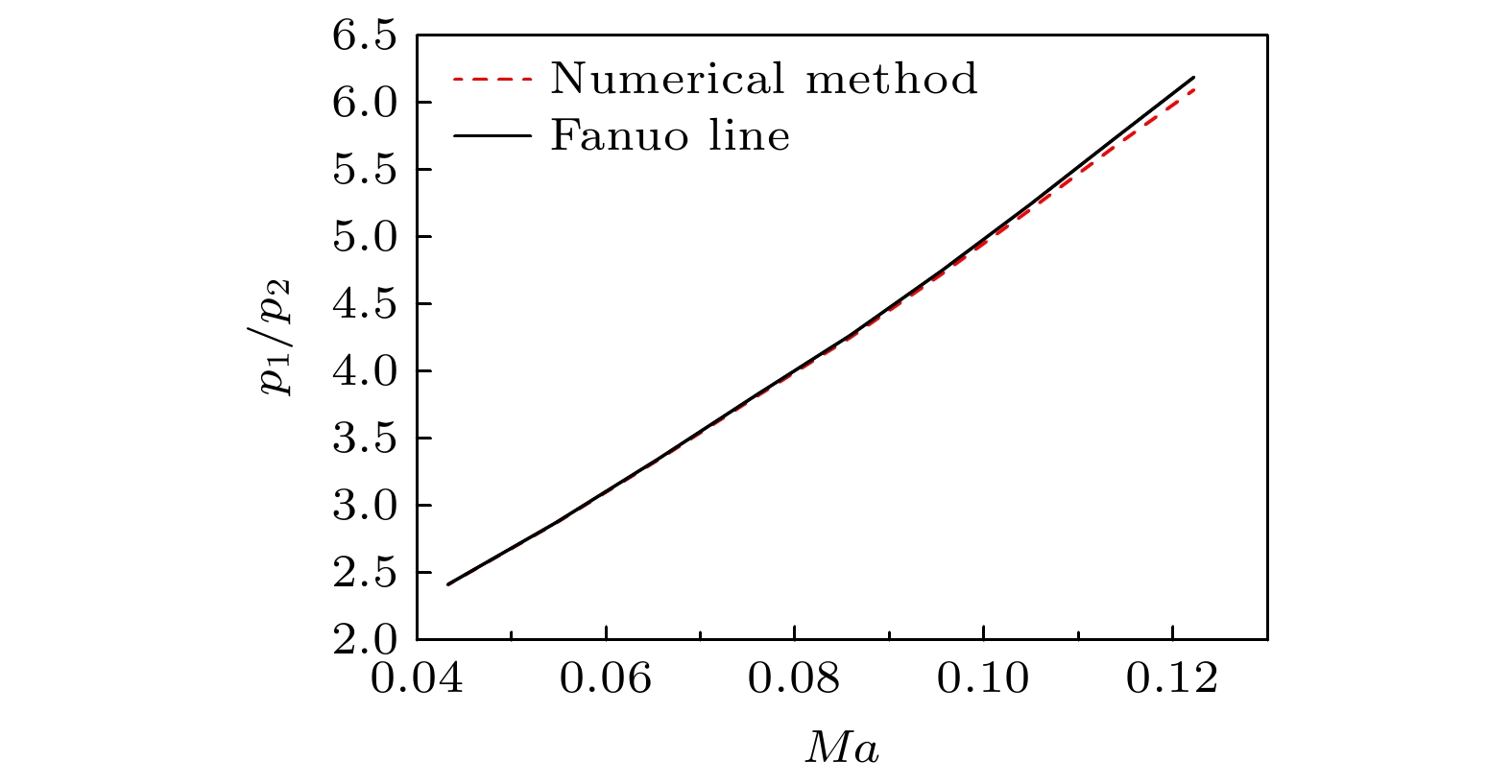
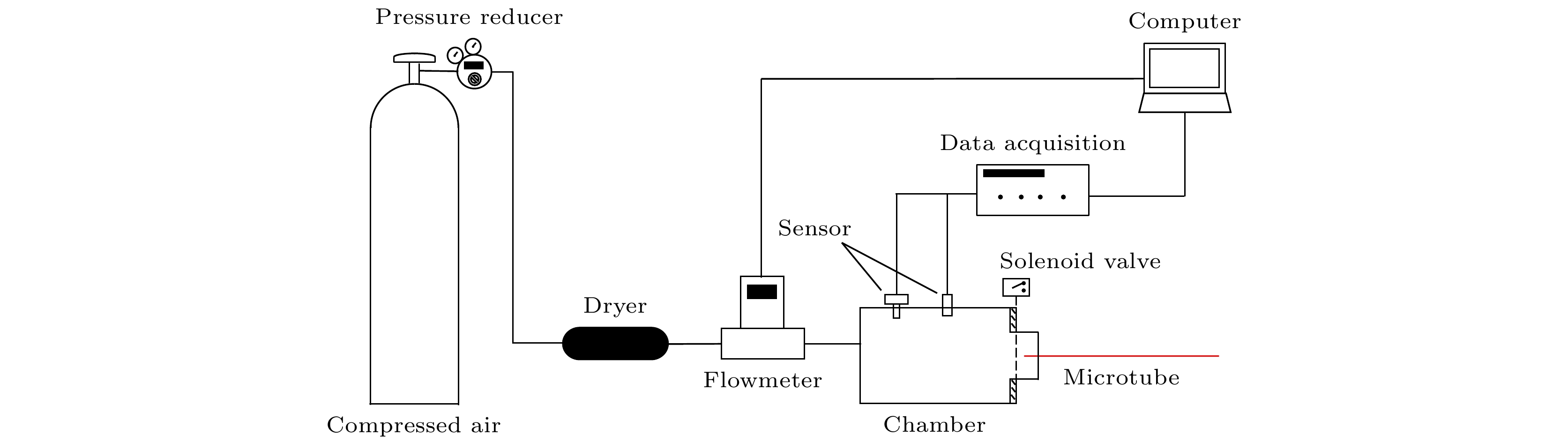
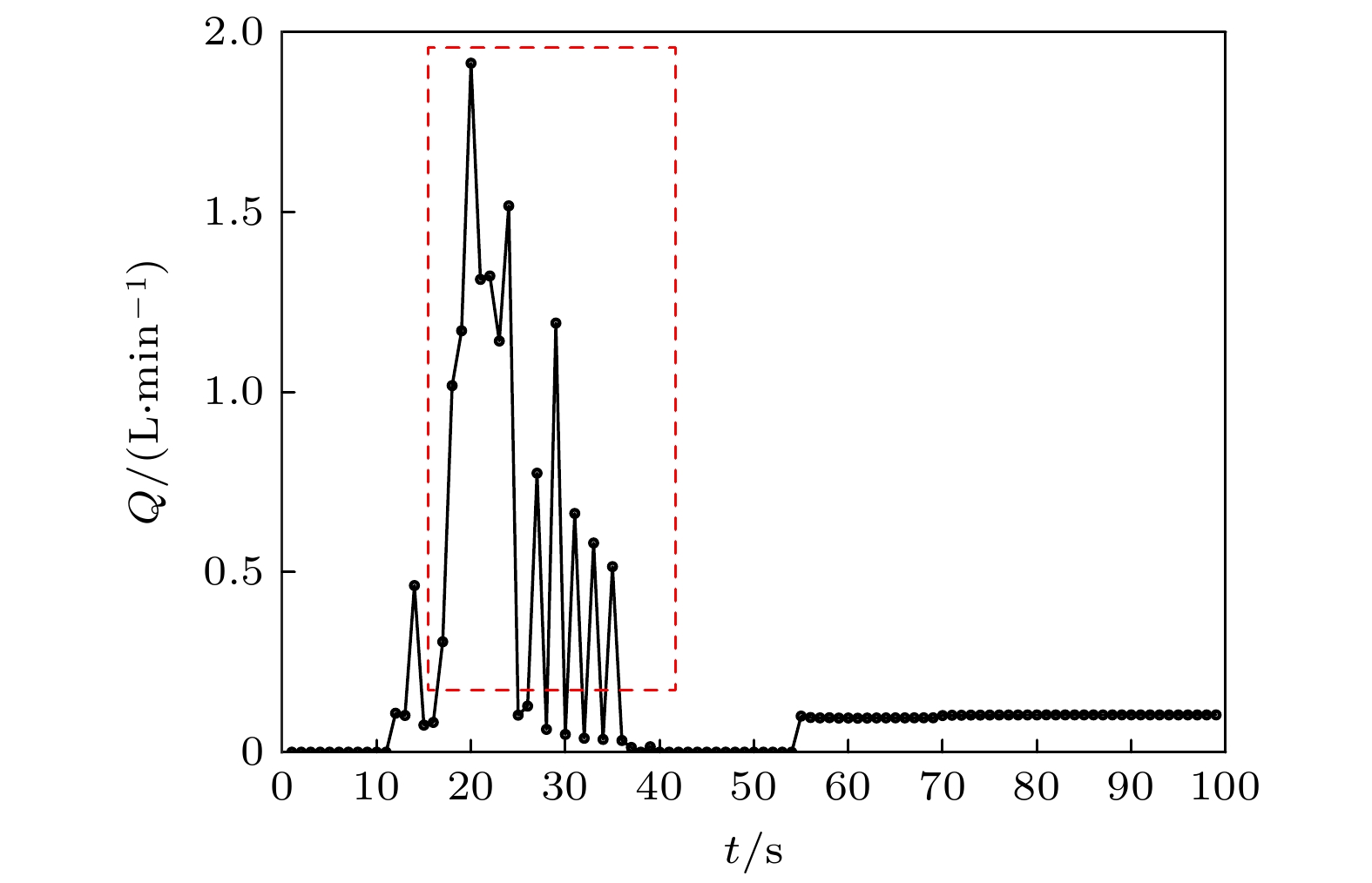
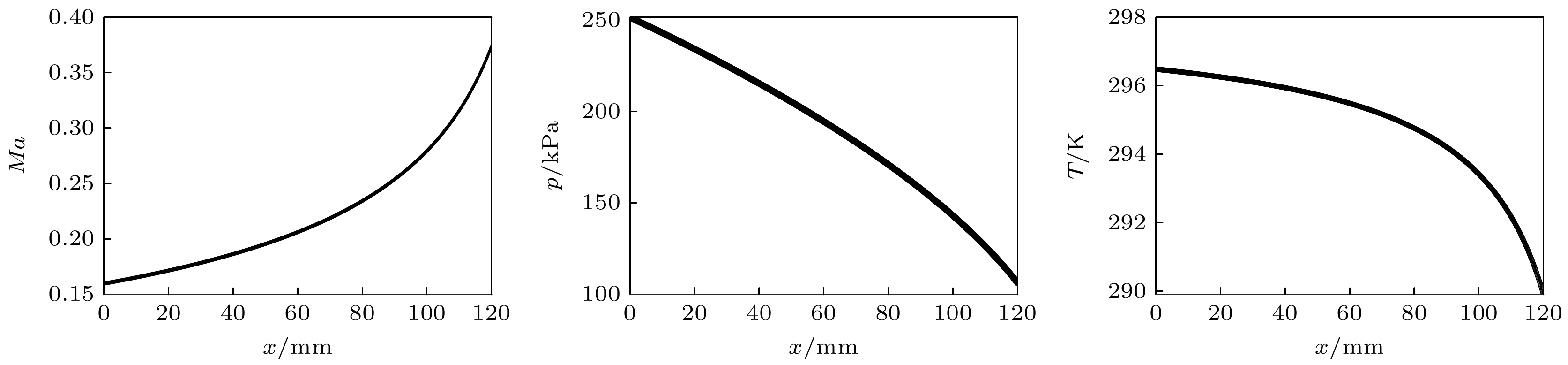
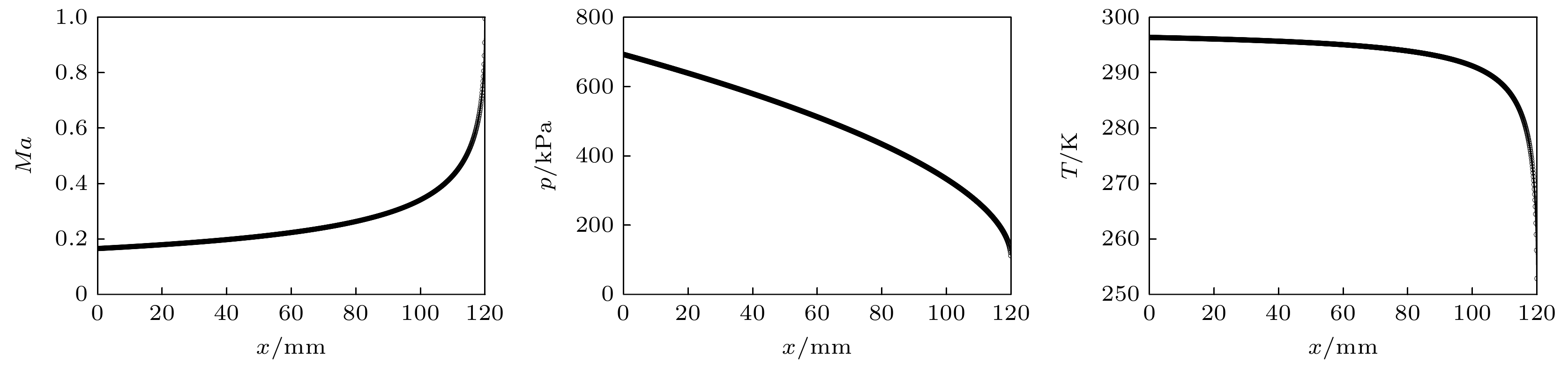
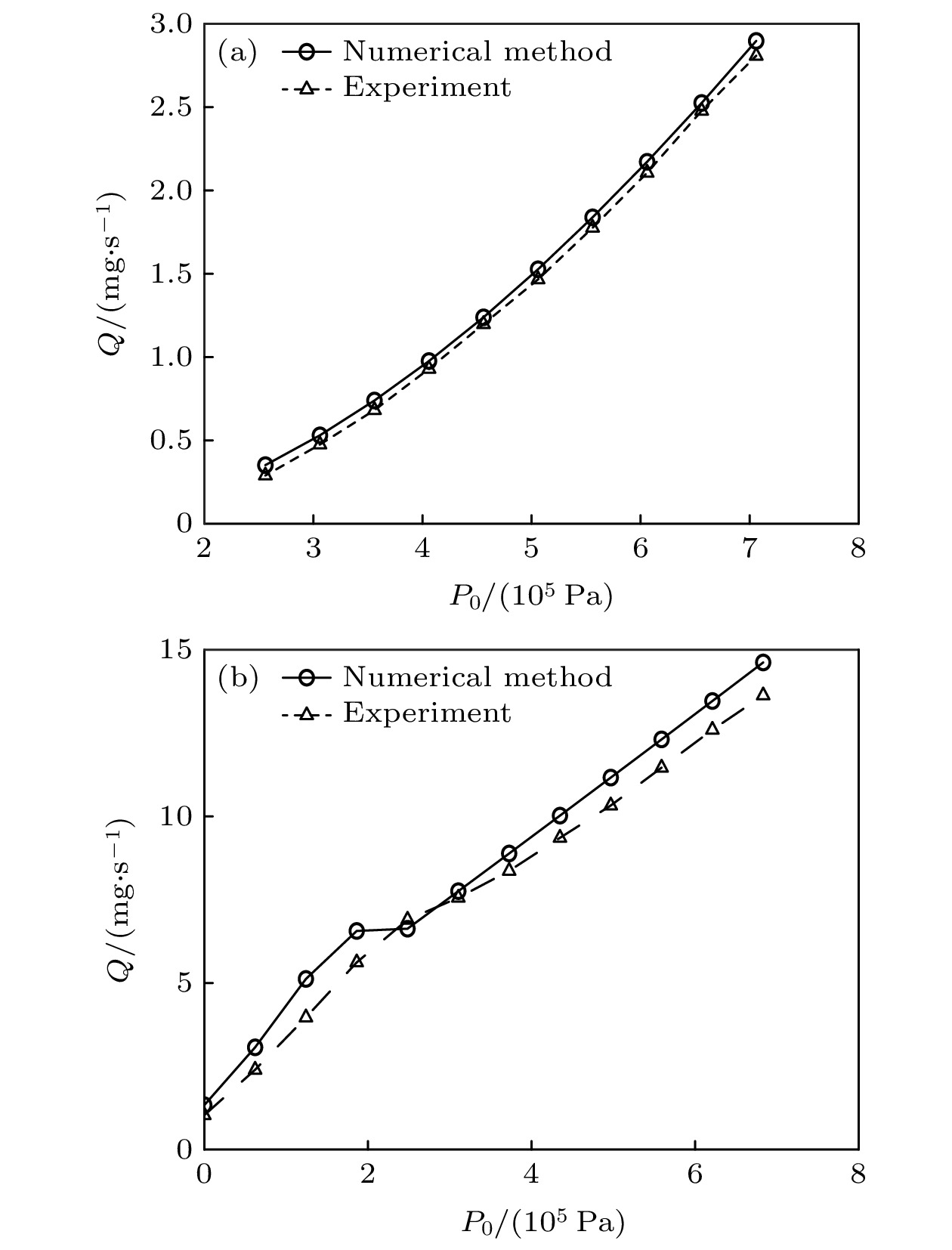
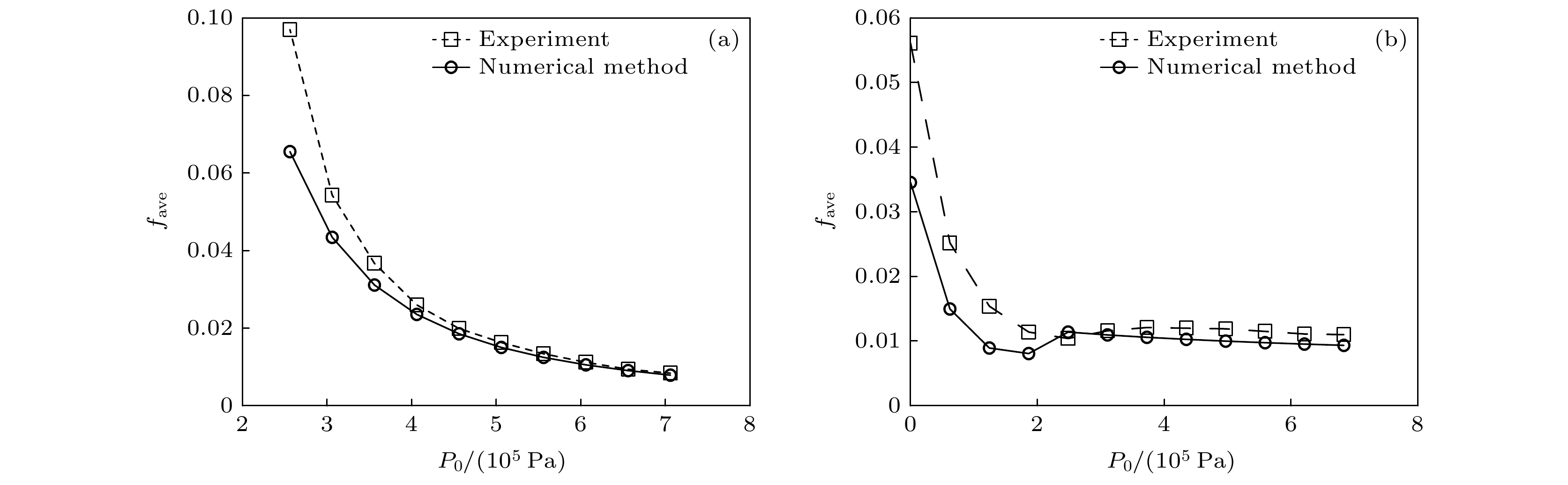
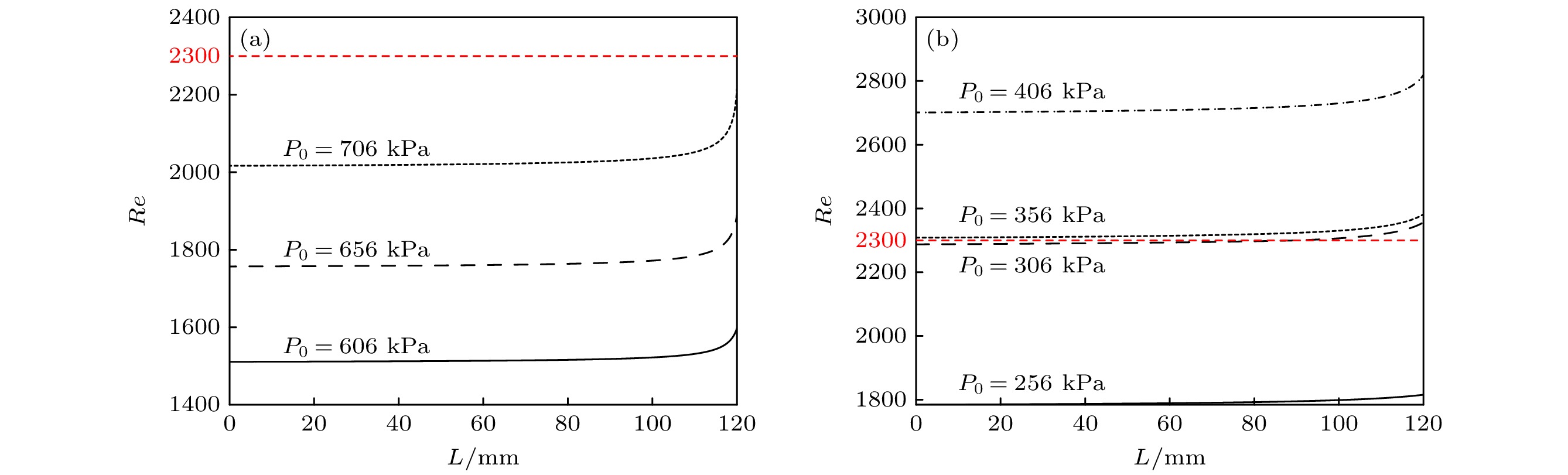
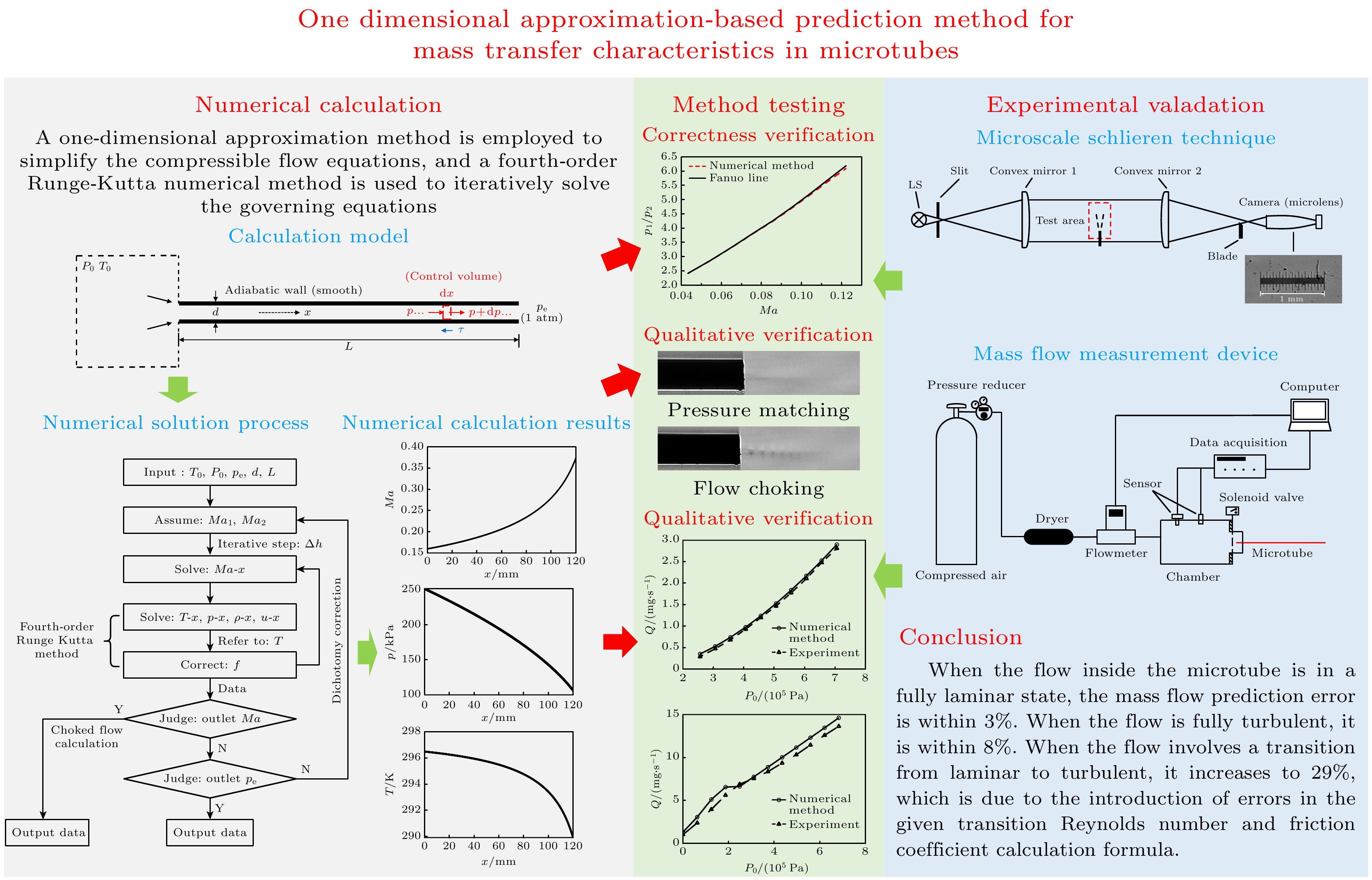
-
The fundamental issues related to heat and mass transfer in microchannels have significant research needs in various engineering fields, such as new materials, microelectronics, and aerospace. This paper addresses the problem of predicting mass transport characteristics within microtubes by developing numerical methods, conducting experimental measurements for validation, and analyzing prediction errors. A one-dimensional approximation method is employed to simplify the compressible flow equations, and a fourth-order Runge-Kutta numerical method is also used to iteratively solve the governing equations. A theoretical calculation method suitable for predicting mass transport characteristics in microtubes is established. This method can calculate various flow parameters along the length of the microtube and can handle different flow conditions, such as static pressure matching or flow choking at the outlet. Subsequently, by comparing the numerical calculation results with the theoretical results of the Fanuo line parameter ratio, the correctness of the numerical calculation method is verified. Also, Schlieren experiments and a self-designed mass flow measurement device are used to qualitatively and quantitatively verify the effectiveness of physical computing models. Under typical driving pressure differences, the qualitative agreement between the calculated and schlieren results for the outlet conditions of the microtube demonstrate the rationality of the numerical method in terms of static pressure matching and flow choking calculations. Regarding mass flow prediction, comparisons between theoretical calculations and experimental measurements under different driving pressures reveal that when the flow inside the microtube is in a fully laminar state, the mass flow prediction error is within 3%. When the flow is fully turbulent, the prediction error is within 8%. However, when the flow involves a transition from laminar to turbulent, the prediction error increases to 29%. During the numerical calculations, based on existing research results, the formula for transition Reynolds number and the turbulent friction factor are set as input parameters . However, the analyses of the Reynolds numbers along the length of the microtube and the average friction factors under different conditions show that the actual transition Reynolds number in the microtube is lower than the value set in the numerical calculations. Additionally, there is a significant discrepancy between the calculated turbulent friction factor and the actual value. Moreover, during the transition from laminar to turbulent flow, the friction factor should increase continuously with the Reynolds number increasing, but the in the numerical calculations the turbulent friction factor is directly used to represent this process. These factors are the main reasons for the larger mass flow prediction errors when the flow involves transition and turbulence. 
-
Keywords:
- one-dimensional processing method /
- mass transfer /
- numerical prediction /
- friction coefficient
-
图 1 计算模型示意图
Figure 1. Schematic diagram of calculation model.
图 2 数值计算流程图
Figure 2. Numerical calculation flow chart.
图 3 数值计算方法与范诺线方程求解p1/p2对比
Figure 3. Comparison of numerical calculation methods and van Gogh line equations for p1/p2.
图 4 实验设置示意图
Figure 4. Schematic diagram of experimental setup.
图 5 石英管截面的电子显微镜图片
Figure 5. Electron microscopy image of quartz tube cross-section.
图 6 典型实验中流量数据曲线
Figure 6. Typical flow data curve in the experiment.
图 7 纹影光路图
Figure 7. Light path diagram of Schlieren.
图 8 成像系统分辨率测试结果
Figure 8. Imaging system resolution test results.
图 9 Case 1直管内沿程Ma, p, T分布
Figure 9. Distribution of Ma, p, and T along the tube of Case1.
图 10 Case 2直管内沿程Ma, p, T分布
Figure 10. Distribution of Ma, p, and T along the tube of Case2.
图 11 纹影实验结果
Figure 11. Experiment results of Schlieren.
图 12 数值计算与实验测量质量流量结果对比 (a) 系列 1 (d = 100 μm); (b) 系列 2 (d = 200 μm)
Figure 12. Comparison of mass flow rate results of numerical calculation and experimental measurement: (a) Series 1 (d = 100 μm); (b) Series 2 (d = 200 μm).
图 13 不同滞止压力时的平均摩擦系数 (a) d = 100 μm; (b) d = 200 μm
Figure 13. Average friction coefficient at different stagnation pressures: (a) d = 100 μm; (b) d = 200 μm.
图 14 不同滞止压力时的沿程雷诺数 (a) d = 100 μm; (b) d = 200 μm
Figure 14. Reynolds numbers along the tube at different stagnation pressures: (a) d = 100 μm; (b) d = 200 μm.
表 1 工况条件
Table 1. Operating conditions.
Case P0/kPa T0 /K pe /kPa d/μm L/mm 1 256 298 106 200 120 2 706 298 106 200 120 
DownLoad: CSV
表 2 计算与实验条件
Table 2. Calculation and experimental conditions.
Series P0 /kPa T0 /K pe /kPa d/μm L/mm 1 256—706 298 106 100 120 2 156—706 298 106 200 120
DownLoad: CSV
-
[1] van den Berg H R, ten Seldam C A, van den Gulik P S 1993 J. Fluid. Mech. 246 1
Google Scholar
[2] Lorenzini M, Morini G L, Salvigni S 2010 Int. J. Therm. 49 248
Google Scholar
[3] Xin Fang, Xiangan Yue, Weiqing An, Xuegang Feng 2019 Microfluid. Nanofluidics. 23 5
Google Scholar
[4] O Reynolds 1883 Philos. Trans. 174 935
Google Scholar
[5] Kawashima D, Yamada T, Hong C, Asako Y 2016 J. Mech. Eng. 230 420
[6] ANSI N14.5 2022. American National Standard for Radioactive Materials Leak -age Teats on Packages for Shipment
[7] Anderson B L, Carlson R W, Fischer L E 1994 Nuclear Regulatory Commission, Washington, DC (United States). Div. of Industrial and Medical Nuclear Safety; Lawrence Livermore National Lab. (LLNL), Livermore, CA, United States
[8] Chen C S, Kuo W J 2004 Numer. Heat. Transfer. 45 85
Google Scholar
[9] Asako Y, Nakayama K, Shinozuka T 2005 Int. J. Heat. Mass. Transfer. 48 4985
Google Scholar
[10] Asako Y, Pi T, Turner S E, Faghri M 2003 Int. J. Heat. Mass. Transfer. 46 3041
Google Scholar
[11] Murakami S, Toyoda K, Asako Y 2021 J. Fluids. Eng. 134 111301
[12] Hong C, Asako Y, Suzuki K, Faghri M 2012 Numer. Heat. Transfer. 61 163
Google Scholar
[13] Hong C, Tanaka G, Asako Y, Katanoda H 2018 Int. J. Heat. Mass. Transfer. 121 187
Google Scholar
[14] Lijo V, Kim H D, Setoguchi T 2012 Int. J. Heat. Mass. Transfer. 55 701
Google Scholar
[15] Wang H, Xing J, Sun Z, Gu H, Sun X, Wang Y 2023 AEST 57 74
[16] Agrawal A, Kushwaha H M, Jadhav R S 2020 Microscale Flow and Heat Transfer (New York: Springer
[17] Shome B 2023 Phys. Fluids 35
[18] Yovanovich M M, Khan W A 2020 J. Thermophys. Heat. Trans. 34 792
Google Scholar
[19] Valougeorgis D 2007 Phys. Fluids 19 091702
Google Scholar
[20] Barber R W, Emerson D R 2006 HTE 27 3
[21] Bykov N Y, Zakharov V V 2022 Phys. Fluids. 34 057106
Google Scholar
[22] Wang X D, Li Y, Gao Y, Gao C G, Fu W C 2023 Aerospace 10 126
Google Scholar
[23] Xu K, Huang J C 2010 J. Comput. Phys. 229 7747
Google Scholar
[24] Guo Z L, Xu K, Wang R J 2013 Phys. Rev. E 88 033305
Google Scholar
[25] Hong C, Yamada T, Asako Y, Faghri M 2012 Int. J. Heat. Mass. Transfer. 55 4397
Google Scholar
[26] Celata G P, Lorenzini M, Morini G L, Zummo G 2009 Int. J. Heat. Fluid. Flow. 30 814
Google Scholar
[27] Rehman D, Barattini D, Hong C, Morini G L 2021 Exp. Fluids 62 52
Google Scholar
[28] Rehman D, Morini G L, Hong C 2019 Micromachines 10 171
Google Scholar
[29] Hong C, Asako Y, Morini G L, Faghri M 2024 Exp. Therm. Fluid. Sci. 155 111196
Google Scholar
[30] Brackbill T, Kandlikar S 2007 Proceedings of the International Conference on Nanochannels, Microchannels and Minichannels Puebla, Mexico, June 18-20, 2007 p509
[31] Eckhardt B, Schneider T M, Hof B, Westerweel J 2007 Annu. Rev. Fluid. Mech. 39 468
[32] Morini G L, Lorenzini M, Salvigni S 2006 Exp. Therm. Fluid. Sci. 30 733
Google Scholar
[33] Du D, Li Z, Guo Z 2000 Sci. China. Technol. Sci. 43 171
Google Scholar
[34] Sonnad J R, Goudar C T 2006 J. Hydraul. Eng 132 863
Google Scholar
[35] 左克罗, 霍夫曼著 (王汝涌, 译) 气体动力学(上册) (北京: 国防工业出版社)
Zucrow M J, Hoffman J D (translated by Wang R Y) 1984 Gas Dynamics (Vol. 1) (Beijing: National Defense Industry Press
[36] Tang G H, Li Z, He Y L, Tao W Q 2007 Int. J. Heat. Mass. Transfer. 50 2282
Google Scholar
[37] Lorenzini M, Morini G L, Salvigni S 2010 Int. J. Therm. Sci. 49 248
Google Scholar
[38] Moody L F 1944 T. ASME 66 671
[39] Avci A, Karagoz I 2019 Eur. J. Mech. B. Fluids 78 182
Google Scholar
DownLoad:
Metrics
- Abstract views: 254
- PDF Downloads: 3
- Cited By: 0
