-
建立了基于第一性原理方法研究二维材料界面摩擦的高通量计算程序, 该程序实现了自动化批量建模、批量提交任务、多任务并发计算, 以及计算结果自动收集、处理和图像绘制, 使用该程序可以节省时间. 采用此程序计算了不同层间距离下双层氮化硼和双层石墨烯的滑移势能面, 及层间界面摩擦力和摩擦系数. 研究发现, 随着层间距离减小, 双层氮化硼界面的平均摩擦力近似线性增大, 摩擦系数为0.11—0.17, 双层石墨烯界面摩擦力先增大后减小再增大, 其摩擦系数在12 nN载荷下达到最小值(0.014), 这些结果与已有研究结果一致, 验证了该计算程序的可靠性. 此外还研究了表面氢化和氟化对双层氮化硼界面摩擦的影响, 发现氟化氮化硼/氮化硼界面的摩擦系数更低.Friction generally occurs in the relative motion or the contact interface with the trend of relative motion, which impedes the relative motion and produces energy loss. Micro-scale friction is different from the macro-scale friction due to surface effects and other factors. It is necessary to study the friction behavior on a nano-scale. First-principles method is an important way to study and understand friction on a nano-scale. Nevertheless, the constructing of nearly a thousand models and the processing of a large number of data are very time consuming. In this paper, we establish a high-throughput computational program based on the first-principles method to study the interfacial friction of two-dimensional materials. The program realizes modeling, submitting computation tasks, multi-task concurrent calculation, data collection and processing, and image rendering of calculation results. All of these are done in batch automatically, which greatly saves researchers’ time. In this work, this program is used to simulate the normal load by changing the distance between layers and calculate the potential energy surface of BN/BN and graphene/graphene bilayer sliding systems at a series of interlayer distances, as well as the interlayer friction forces and friction coefficients. The study finds that with the decrease of the interlayer distance, the averaged friction force at BN/BN interface increases approximately linearly, and the friction coefficient is in a range of 0.11–0.17. The friction force at graphene/graphene interface first increases, then decreases, and increases again. The friction coefficient reaches a minimum value (0.014) under a load of 12 nN, and these results are consistent with the previous results, verifying the reliability of the calculation program. In addition, we investigate the effect of surface hydrogenation and fluorination on the tribological property of the BN bilayer and find that the friction at the fluorinated BN/BN interface decreases, which is attributed to the smaller charge transfer at interface. Although the high-throughput calculation method realizes the automation and high-throughput calculation of tribological property at solid interface, there are still some limitations. Firstly, the effect of interlaminar bending is not considered in the process of interlaminar relative sliding. Secondly, the essence of the calculation result is static friction, rather than dynamic friction. In addition, the method does not consider the influence of temperature.
-
Keywords:
- first-principles method /
- high-throughput calculation /
- potential energy surface /
- friction coefficient
[1] Holmberg K, Andersson P, Nylund N O, Makela K, Erdemir A 2014 Tribol. Int. 78 94
Google Scholar
[2] Carpick R W 2006 Science. 313 184
Google Scholar
[3] Zhuang C Q, Liu L 2017 Aip Adv. 7 085103
Google Scholar
[4] Berman D, Erdemir A, Sumant A V 2018 Acs Nano. 12 2122
Google Scholar
[5] Yuan J H, Yang R, Zhang G Y 2022 Nanotechnology 33 102002
Google Scholar
[6] Marchetto D, Feser T, Dienwiebel M 2015 Friction 3 161
Google Scholar
[7] Kimura Y, Wakabayashi T, Okada K, Wada T, Nishikawa H 1999 Wear 232 199
Google Scholar
[8] Dominguez-Meister S, Rojas T C, Brizuela M, Sanchez-Lopez J C 2017 Sci. Technol. Adv. Mat. 18 122
Google Scholar
[9] Zhao X Y, Hamilton M, Sawyer W G, Perry S S 2007 Tribol. Lett. 27 113
Google Scholar
[10] Schirmeisen A, Jansen L, Holscher H, Fuchs H 2006 Appl. Phys. Lett. 88 607
[11] Tshiprut Z, Zelner S, Urbakh M 2009 Phys. Rev. Lett. 102 136102
Google Scholar
[12] Weiss M, Majchrzycki L, Borkowska E, Cichomski M, Ptak A 2021 Tribol. Int. 162 107133
Google Scholar
[13] Luan B Q, Robbins M O 2005 Nature 435 929
Google Scholar
[14] Riedo E, Pallaci I, Boragno C, Brune H 2004 J. Phys. Chem. B 108 5324
Google Scholar
[15] He X, Liu Z, Ripley L B, Swensen V L, Griffin-Wiesner I J, Gulner B R, McAndrews G R, Wieser R J, Borovsky B P, Wang Q J, Kim S H 2021 Tribol. Int. 155 106780
Google Scholar
[16] Ru G L, Qi W H, Tang K W, Wei Y R, Xue T W 2020 Tribol. Int. 151 106483
Google Scholar
[17] Ru G L, Qi W H, Wei Y R, Tang K W, Xue T W 2021 Tribol. Int. 159 106974
Google Scholar
[18] Dong Y, Perez D, Gao H, Martini A 2012 J. Phys-Condens Mat. 24 265001
Google Scholar
[19] Zworner O, Holscher H, Schwarz U D, Wiesendanger R 1998 Appl. Phys. A-Mater. 66 S263
Google Scholar
[20] Fajardo O Y, Barel I, Urbakh M 2014 J. Phys-Condens Mat. 26 315002
Google Scholar
[21] Mate C M, Mcclelland G M, Erlandsson R, Chiang S 1987 Phys. Rev. Lett. 59 1942
Google Scholar
[22] Mo Y F, Turner K T, Szlufarska I 2009 Nature 457 1116
Google Scholar
[23] An X H, Yao H J, Ma F, Lu Z B 2015 Rsc Adv. 5 106239
Google Scholar
[24] Sun J H, Zhang Y N, Lu Z B, Li Q Y, Xue Q J, Du S Y, Pu J B, Wang L P 2018 J. Phys. Chem. Lett. 9 2554
Google Scholar
[25] Cheng Z W, Sun J H, Zhang B Z, Lu Z B, Ma F, Zhang G A, Xue Q J 2020 J. Phys. Chem. Lett. 11 5815
Google Scholar
[26] Wang K B, Li H, Guo Y F 2021 Materials 14 4717
Google Scholar
[27] Wang J J, Wang F, Li J M, Wang S J, Song Y L, Sun Q, Jia Y 2012 Tribol. Lett. 48 255
Google Scholar
[28] Gao W, Tkatchenko A 2015 Phys. Rev. Lett. 114 096101
Google Scholar
[29] Zhuang C Q, Liu L 2015 J. Appl. Phys. 117 114302
Google Scholar
[30] Ko J H, Kwon S, Byun I S, Choi J S, Park B H, Kim Y H, Park J Y 2013 Tribol. Lett. 50 137
Google Scholar
[31] Qu C Y, Wang K Q, Wang J, Gongyang Y J, Carpick R W, Urbakh M, Zheng Q S 2020 Phys. Rev. Lett. 125 12
[32] Ruan X, Shi J, Wang X, Wang W Y, Fan X, Zhou F 2021 ACS Appl. Mater. Interfaces 13 40901
Google Scholar
[33] Liao M Z, Nicolini P, Du L J, Yuan J H, Wang S P, Yu H, Tang J, Cheng P, Watanabe K, Taniguchi T, Gu L, Claerbout V E P, Silva A, Kramer D, Polcar T, Yang R, Shi D X, Zhang G Y 2022 Nat. Mater. 21 47
Google Scholar
[34] Li S Z, Li Q Y, Carpick R W, Gumbsch P, Liu X Z, Ding X D, Sun J, Li J 2016 Nature 539 541
Google Scholar
[35] Filippov A E, Dienwiebel M, Frenken J W M, Klafter J, Urbakh M 2008 Phys. Rev. Lett. 100 046102
Google Scholar
[36] Zhang J, Bai Y, An L, Zhang B, Zhang J, Yu Y, Wang C M 2019 J. Appl. Phys. 126 035104
Google Scholar
[37] Cheng Z W, An X H, Wang J J, Zhang B Z, Lu Z B, Zhang G G 2020 Tribol. Int. 141 105961
Google Scholar
[38] Wang J J, Li J M, Fang L L, Sun Q, Jia Y 2014 Tribol. Lett. 55 405
Google Scholar
[39] Restuccia P, Levita G, Wolloch M, Losi G, Fatti G, Ferrario M, Righi M C 2018 Comp. Mater. Sci. 154 517
Google Scholar
[40] Gonze X, Ghosez P, Godby R W 1997 Phys. Rev. Lett. 78 294
Google Scholar
[41] Kresse G 1995 J. Non-Cryst. Solids 193 222
[42] Kresse G, Furthmuller J 1996 Comp. Mater. Sci. 6 15
Google Scholar
[43] Kresse G, Furthmuller J 1996 Phys. Rev. B 54 11169
Google Scholar
[44] Weinan E, Ren W Q, Vanden-Eijnden E 2002 Phys. Rev. B 66 052301
[45] Zhong W, Tomanek D 1990 Phys. Rev. Lett. 64 3054
Google Scholar
[46] Perdew J P, Burke K, Ernzerhof M 1997 Phys. Rev. Lett. 78 1396
[47] Kresse G, Joubert D 1999 Phys. Rev. B 59 1758
[48] Wang V, Xu N, Liu J C, Tang G, Geng W T 2021 Comput. Phys. Commun. 267 108033
Google Scholar
[49] Marom N, Bernstein J, Garel J, Tkatchenko A, Joselevich E, Kronik L, Hod O 2010 Phys. Rev. Lett. 105 046801
Google Scholar
[50] Martin J M, Lemogne T, Chassagnette C, Gardos M N 1992 Tribol. T. 35 462
Google Scholar
[51] Wang W, Xie G X, Luo J B 2018 Friction 6 116
Google Scholar
[52] Zhang B Z, Zhang G G, Cheng Z W, Ma F, Lu Z B 2019 Appl. Surf. Sci. 483 742
Google Scholar
[53] Fan K, Chen X Y, Wang X, Liu X K, Liu Y, Lai W C, Liu X Y 2018 Acs Appl. Mater. Interfaces 10 28828
Google Scholar
[54] Cahangirov S, Ciraci S, Ozcelik V O 2013 Phys. Rev. B 87 205428
Google Scholar
[55] Li Q Y, Liu X Z, Kim S P, Shenoy V B, Sheehan P E, Robinson J T, Carpick R W 2014 Nano Lett. 14 5212
Google Scholar
[56] Wolloch M, Levita G, Restuccia P, Righi M C 2018 Phys. Rev. Lett. 121 026804
-
图 1 二维材料界面摩擦学特性高通量计算流程示意图
Fig. 1. The schematic diagram showing the procedure of high-throughput calculation of the tribological property at the interface of two-dimensional materials.
图 2 BN/BN, H-BN/BN 和 F-BN/BN 双层体系原子结构的俯视图和侧视图 (a) Top和(b) Hollow位置BN/BN的俯视图和侧视图; (c) H-BN/BN和(d) F-BN/BN在Hollow位置的俯视图和侧视图
Fig. 2. Top and side views for atomic structures of BN/BN, H-BN/BN, and F-BN/BN bilayer. Top and side views of BN/BN bilayer in (a) Top and (b) Hollow positions. Top and side views of (c) H-BN/BN and (d) F-BN/BN bilayers in Hollow position.
图 3 BN/BN位于Top位置的界面结合能和载荷随层间距的变化 (a) 结合能; (b) 载荷
Fig. 3. The variation of interlayer binding energy (
$ {E}_{\rm{b}} $ ) and load with interlayer distance for BN/BN bilayer at Top position: (a)$ {E}_{\rm{b}} $ and (b) load.
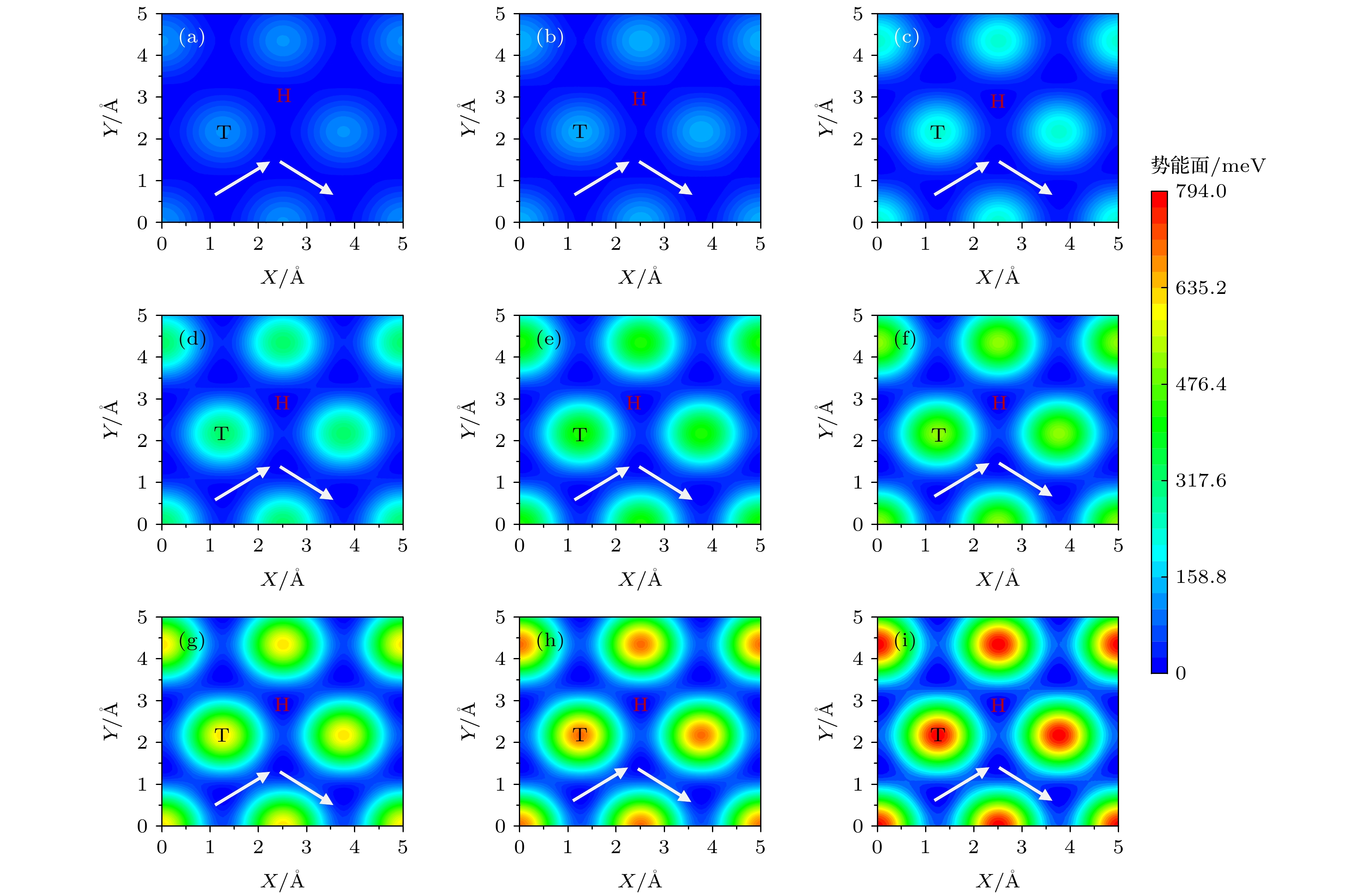
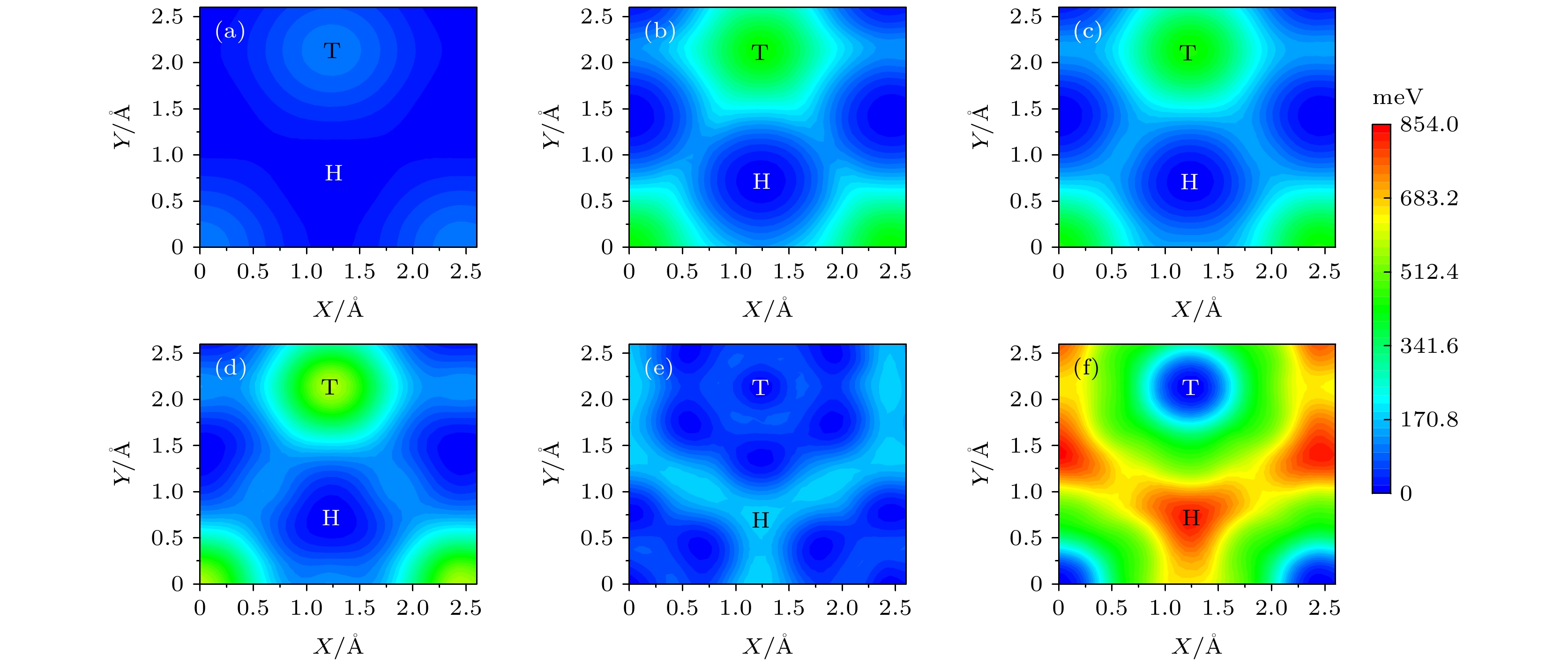
图 4 不同载荷下BN/BN的势能面 (a) 0 nN; (b) 1 nN; (c) 2 nN; (d) 3 nN; (e) 4 nN; (f) 5 nN; (g) 6 nN; (h) 7 nN; (i) 8 nN. T和H分别表示Top和Hollow位置, 白色带箭头线代表最小能量路径
Fig. 4. Potential energy surface of BN/BN bilayer under normal load of (a) 0 nN, (b) 1 nN, (c) 2 nN, (d) 3 nN, (e) 4 nN, (f) 5 nN, (g) 6 nN, (h) 7 nN and (i) 8 nN. T and H present the Top and Hollow positions, respectively. The white lines with arrow represent the minimum energy path.
图 5 0—8 nN载荷下BN/BN最小能量路径上势能的变化
Fig. 5. The variation of potential energy along the minimum energy path of BN/BN bilayer under 0–8 nN loads.
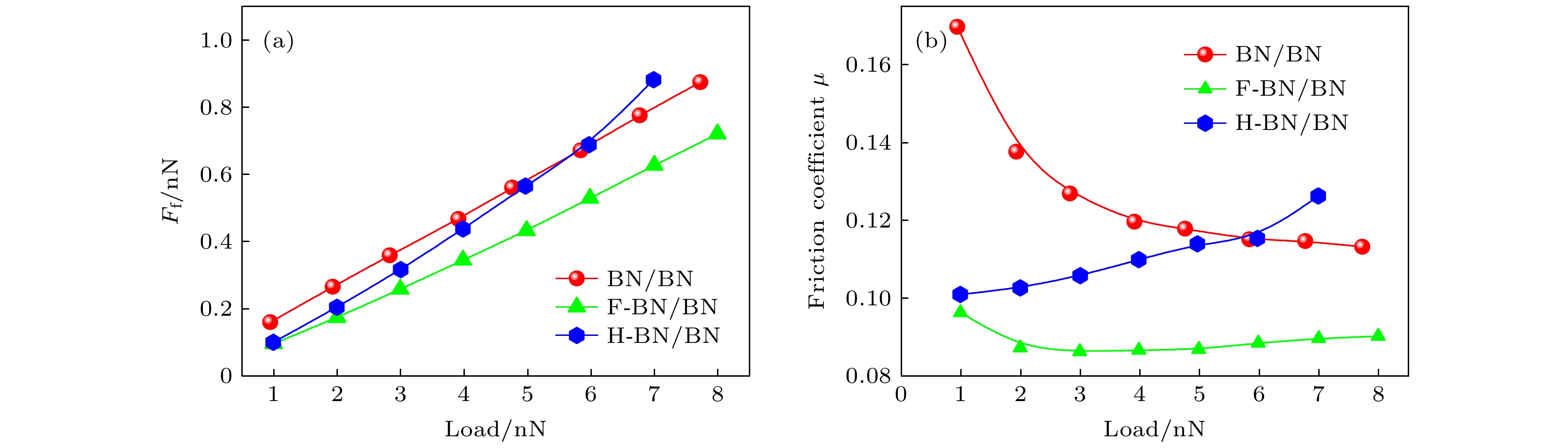
图 6 BN/BN, F-BN/BN, H-BN/BN的平均界面摩擦力(
$ {F}_{\rm{f}} $ )和摩擦系数($ \mu $ )随载荷的变化 (a)平均摩擦力; (b)摩擦系数Fig. 6. The variation of friction force at the interface of BN/BN, F-BN/BN, and H-BN/BN bilayers with respect to the normal load: (a) Averaged interfacial friction (
$ {F}_{\rm{f}} $ ); (b) friction coefficient ($ \mu $ ).
图 7 不同载荷下Gr/Gr的势能面 (a) 1 nN; (b) 4 nN; (c) 7 nN; (d) 10 nN; (e) 12 nN; (f) 13.5 nN. (a)—(d)中的H/T对应最小/最大势能, 而(e), (f)中的H/T对应最大/最小势能
Fig. 7. Potential energy surface of graphene/graphene (Gr/Gr) bilayer under normal load of (a) 1 nN, (b) 4 nN, (c) 7 nN, (d) 10 nN, (e) 12 nN, and (f) 13.5 nN. T and H present the top and hollow positions, respectively. H/T in (a)–(d) is the position of minimum/maximum potential energy, whereas, T/H in (e), (f) is the position of minimum/maximum potential energy.
图 8 Gr/Gr界面平均摩擦力和摩擦系数随载荷的变化 (a)平均摩擦力; (b)摩擦系数
Fig. 8. The variation of friction force at the interface of graphene/graphene (Gr/Gr) bilayers with respect to the normal load: (a) Averaged interfacial friction and (b) friction coefficient.
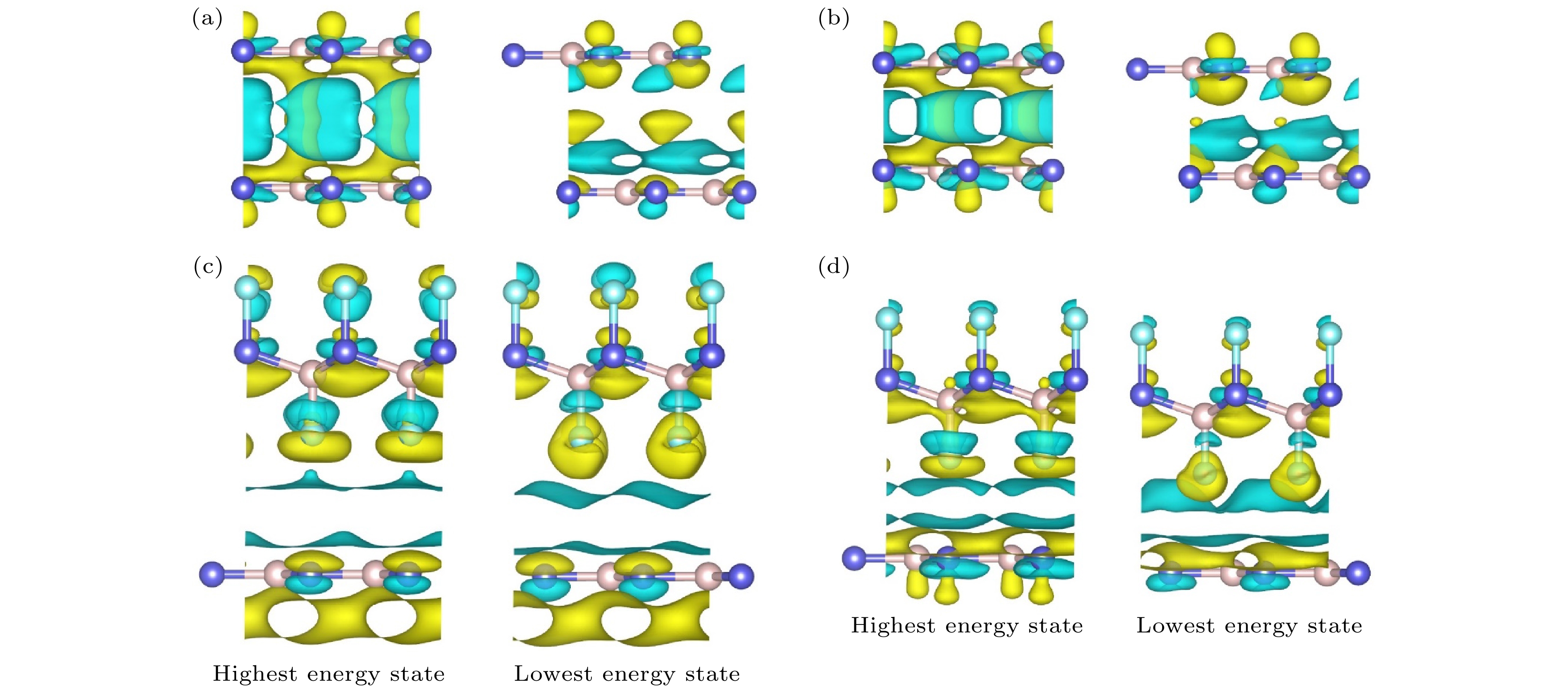
图 9 BN/BN和F-BN/BN的最高和最低势能态在0 nN和8 nN载荷下的差分电荷密度 (a) BN/BN, 0 nN; (b) BN/BN, 8 nN; (c) F-BN/BN, 0 nN; (d) F-BN/BN, 8 nN. 黄色代表电子聚集, 蓝色代表电子损失; 左边和右边的图分别对应最高和最低势能态; 图(a)和(c)中的等值面设置为0.00006e/Bohr3; 图 (b) 和 (d) 中的等值面设置为0.0003e/Bohr3
Fig. 9. Differential charge density of BN/BN and F-BN/BN bilayer at the highest and lowest potential energy state under 0 nN and 8 nN loads. BN/BN bilayer under (a) 0 nN and (b) 8 nN load, F-BN/BN bilayer under (c) 0 nN and (d) 8 nN loads. The yellow color represents electron aggregation, and the blue color represents electron dissipation. The isosurface value in figure (a) and (c) is set to 0.00006e/Bohr3; the isosurface value in figure (b) and (d) is set to 0.0003e/Bohr3.
-
[1] Holmberg K, Andersson P, Nylund N O, Makela K, Erdemir A 2014 Tribol. Int. 78 94
Google Scholar
[2] Carpick R W 2006 Science. 313 184
Google Scholar
[3] Zhuang C Q, Liu L 2017 Aip Adv. 7 085103
Google Scholar
[4] Berman D, Erdemir A, Sumant A V 2018 Acs Nano. 12 2122
Google Scholar
[5] Yuan J H, Yang R, Zhang G Y 2022 Nanotechnology 33 102002
Google Scholar
[6] Marchetto D, Feser T, Dienwiebel M 2015 Friction 3 161
Google Scholar
[7] Kimura Y, Wakabayashi T, Okada K, Wada T, Nishikawa H 1999 Wear 232 199
Google Scholar
[8] Dominguez-Meister S, Rojas T C, Brizuela M, Sanchez-Lopez J C 2017 Sci. Technol. Adv. Mat. 18 122
Google Scholar
[9] Zhao X Y, Hamilton M, Sawyer W G, Perry S S 2007 Tribol. Lett. 27 113
Google Scholar
[10] Schirmeisen A, Jansen L, Holscher H, Fuchs H 2006 Appl. Phys. Lett. 88 607
[11] Tshiprut Z, Zelner S, Urbakh M 2009 Phys. Rev. Lett. 102 136102
Google Scholar
[12] Weiss M, Majchrzycki L, Borkowska E, Cichomski M, Ptak A 2021 Tribol. Int. 162 107133
Google Scholar
[13] Luan B Q, Robbins M O 2005 Nature 435 929
Google Scholar
[14] Riedo E, Pallaci I, Boragno C, Brune H 2004 J. Phys. Chem. B 108 5324
Google Scholar
[15] He X, Liu Z, Ripley L B, Swensen V L, Griffin-Wiesner I J, Gulner B R, McAndrews G R, Wieser R J, Borovsky B P, Wang Q J, Kim S H 2021 Tribol. Int. 155 106780
Google Scholar
[16] Ru G L, Qi W H, Tang K W, Wei Y R, Xue T W 2020 Tribol. Int. 151 106483
Google Scholar
[17] Ru G L, Qi W H, Wei Y R, Tang K W, Xue T W 2021 Tribol. Int. 159 106974
Google Scholar
[18] Dong Y, Perez D, Gao H, Martini A 2012 J. Phys-Condens Mat. 24 265001
Google Scholar
[19] Zworner O, Holscher H, Schwarz U D, Wiesendanger R 1998 Appl. Phys. A-Mater. 66 S263
Google Scholar
[20] Fajardo O Y, Barel I, Urbakh M 2014 J. Phys-Condens Mat. 26 315002
Google Scholar
[21] Mate C M, Mcclelland G M, Erlandsson R, Chiang S 1987 Phys. Rev. Lett. 59 1942
Google Scholar
[22] Mo Y F, Turner K T, Szlufarska I 2009 Nature 457 1116
Google Scholar
[23] An X H, Yao H J, Ma F, Lu Z B 2015 Rsc Adv. 5 106239
Google Scholar
[24] Sun J H, Zhang Y N, Lu Z B, Li Q Y, Xue Q J, Du S Y, Pu J B, Wang L P 2018 J. Phys. Chem. Lett. 9 2554
Google Scholar
[25] Cheng Z W, Sun J H, Zhang B Z, Lu Z B, Ma F, Zhang G A, Xue Q J 2020 J. Phys. Chem. Lett. 11 5815
Google Scholar
[26] Wang K B, Li H, Guo Y F 2021 Materials 14 4717
Google Scholar
[27] Wang J J, Wang F, Li J M, Wang S J, Song Y L, Sun Q, Jia Y 2012 Tribol. Lett. 48 255
Google Scholar
[28] Gao W, Tkatchenko A 2015 Phys. Rev. Lett. 114 096101
Google Scholar
[29] Zhuang C Q, Liu L 2015 J. Appl. Phys. 117 114302
Google Scholar
[30] Ko J H, Kwon S, Byun I S, Choi J S, Park B H, Kim Y H, Park J Y 2013 Tribol. Lett. 50 137
Google Scholar
[31] Qu C Y, Wang K Q, Wang J, Gongyang Y J, Carpick R W, Urbakh M, Zheng Q S 2020 Phys. Rev. Lett. 125 12
[32] Ruan X, Shi J, Wang X, Wang W Y, Fan X, Zhou F 2021 ACS Appl. Mater. Interfaces 13 40901
Google Scholar
[33] Liao M Z, Nicolini P, Du L J, Yuan J H, Wang S P, Yu H, Tang J, Cheng P, Watanabe K, Taniguchi T, Gu L, Claerbout V E P, Silva A, Kramer D, Polcar T, Yang R, Shi D X, Zhang G Y 2022 Nat. Mater. 21 47
Google Scholar
[34] Li S Z, Li Q Y, Carpick R W, Gumbsch P, Liu X Z, Ding X D, Sun J, Li J 2016 Nature 539 541
Google Scholar
[35] Filippov A E, Dienwiebel M, Frenken J W M, Klafter J, Urbakh M 2008 Phys. Rev. Lett. 100 046102
Google Scholar
[36] Zhang J, Bai Y, An L, Zhang B, Zhang J, Yu Y, Wang C M 2019 J. Appl. Phys. 126 035104
Google Scholar
[37] Cheng Z W, An X H, Wang J J, Zhang B Z, Lu Z B, Zhang G G 2020 Tribol. Int. 141 105961
Google Scholar
[38] Wang J J, Li J M, Fang L L, Sun Q, Jia Y 2014 Tribol. Lett. 55 405
Google Scholar
[39] Restuccia P, Levita G, Wolloch M, Losi G, Fatti G, Ferrario M, Righi M C 2018 Comp. Mater. Sci. 154 517
Google Scholar
[40] Gonze X, Ghosez P, Godby R W 1997 Phys. Rev. Lett. 78 294
Google Scholar
[41] Kresse G 1995 J. Non-Cryst. Solids 193 222
[42] Kresse G, Furthmuller J 1996 Comp. Mater. Sci. 6 15
Google Scholar
[43] Kresse G, Furthmuller J 1996 Phys. Rev. B 54 11169
Google Scholar
[44] Weinan E, Ren W Q, Vanden-Eijnden E 2002 Phys. Rev. B 66 052301
[45] Zhong W, Tomanek D 1990 Phys. Rev. Lett. 64 3054
Google Scholar
[46] Perdew J P, Burke K, Ernzerhof M 1997 Phys. Rev. Lett. 78 1396
[47] Kresse G, Joubert D 1999 Phys. Rev. B 59 1758
[48] Wang V, Xu N, Liu J C, Tang G, Geng W T 2021 Comput. Phys. Commun. 267 108033
Google Scholar
[49] Marom N, Bernstein J, Garel J, Tkatchenko A, Joselevich E, Kronik L, Hod O 2010 Phys. Rev. Lett. 105 046801
Google Scholar
[50] Martin J M, Lemogne T, Chassagnette C, Gardos M N 1992 Tribol. T. 35 462
Google Scholar
[51] Wang W, Xie G X, Luo J B 2018 Friction 6 116
Google Scholar
[52] Zhang B Z, Zhang G G, Cheng Z W, Ma F, Lu Z B 2019 Appl. Surf. Sci. 483 742
Google Scholar
[53] Fan K, Chen X Y, Wang X, Liu X K, Liu Y, Lai W C, Liu X Y 2018 Acs Appl. Mater. Interfaces 10 28828
Google Scholar
[54] Cahangirov S, Ciraci S, Ozcelik V O 2013 Phys. Rev. B 87 205428
Google Scholar
[55] Li Q Y, Liu X Z, Kim S P, Shenoy V B, Sheehan P E, Robinson J T, Carpick R W 2014 Nano Lett. 14 5212
Google Scholar
[56] Wolloch M, Levita G, Restuccia P, Righi M C 2018 Phys. Rev. Lett. 121 026804
-
[1] 李文涛, 袁美玲, 王杰敏. C++H2反应的动力学研究: 基于一个新构建的势能面. , 2022, 71(9): 093402. doi: 10.7498/aps.71.20212241 [2] 袁俊鹏, 刘秀英, 李晓东, 于景新. 沸石分子筛对CH4/H2的吸附与分离性能. , 2021, 70(15): 156801. doi: 10.7498/aps.70.20210101 [3] 彭军辉, TikhonovEvgenii. 三元Hf-C-N体系的空位有序结构及其力学性质和电子性质的第一性原理研究. , 2021, 70(21): 216101. doi: 10.7498/aps.70.20210244 [4] 苏文霞, 陆海鸣, 曾子芮, 张一飞, 刘剑, 徐坤, 王敦辉, 都有为. 磁制冷材料LaFe11.5Si1.5基合金成分与磁相变温度关系的高通量计算. , 2021, 70(20): 207501. doi: 10.7498/aps.70.20211085 [5] 吴思远, 王宇琦, 肖睿娟, 陈立泉. 电池材料数据库的发展与应用. , 2020, 69(22): 226104. doi: 10.7498/aps.69.20201542 [6] 李君, 刘立胜, 徐爽, 张金咏. 单轴压缩下Ti3B4的力学、电学性能及变形机制的第一性原理研究. , 2020, 69(4): 043102. doi: 10.7498/aps.69.20191194 [7] 赵文丽, 王永刚, 张路路, 岳大光, 孟庆田. 基于新CH2( ${\tilde {\bf{X}}{}^3}{\bf{A''}}$ )势能面的${\bf C}{\bf({}^3}{\bf{P})} + {\bf{H}_2(}{\bf X^1}\Sigma _{\bf g}^ + {\bf )} $ $ \to {\bf H({}^2}{\bf S}) + {\bf CH}{(\bf{}^2}\Pi ) $ 反应量子波包动力学. , 2020, 69(8): 083401. doi: 10.7498/aps.69.20200132[8] 郑麟, 莫松平, 李玉秀, 陈颖, 徐进良. 薄层剪切二元颗粒分离过程动力学特性分析. , 2019, 68(16): 164703. doi: 10.7498/aps.68.20190322 [9] 杨雪, 闫冰, 连科研, 丁大军. 1,2-环己二酮基态光解离反应的理论研究. , 2015, 64(21): 213101. doi: 10.7498/aps.64.213101 [10] 王欣欣, 张颖, 周洪波, 王金龙. 铌对钨中氦行为影响的第一性原理研究. , 2014, 63(4): 046103. doi: 10.7498/aps.63.046103 [11] 金硕, 孙璐. 带有碳杂质的钨中氢稳定性的第一性原理研究. , 2012, 61(4): 046104. doi: 10.7498/aps.61.046104 [12] 韩亮, 宁涛, 刘德连, 何亮. 氩离子轰击对四面体非晶碳膜内应力和摩擦系数影响的研究. , 2012, 61(17): 176801. doi: 10.7498/aps.61.176801 [13] 韩亮, 杨立, 杨拉毛草, 王炎武, 赵玉清. 磁过滤器电流对非晶碳薄膜摩擦学特性影响的研究. , 2011, 60(4): 046802. doi: 10.7498/aps.60.046802 [14] 韩亮, 陈仙, 杨立, 王炎武, 王晓艳, 赵玉清. 高能氮离子轰击对四面体非晶碳膜的表面改性和摩擦系数影响的研究. , 2011, 60(6): 066804. doi: 10.7498/aps.60.066804 [15] 原鹏飞, 祝文军, 徐济安, 刘绍军, 经福谦. BeO高压相变和声子谱的第一性原理计算. , 2010, 59(12): 8755-8761. doi: 10.7498/aps.59.8755 [16] 龚博致, 张秉坚. 水中自然超空泡机理及减阻效应的非平衡分子动力学研究. , 2009, 58(3): 1504-1509. doi: 10.7498/aps.58.1504 [17] 余春日, 凤尔银, 程新路, 杨向东. He-HI复合物势能面及微分散射截面的理论研究. , 2007, 56(8): 4441-4447. doi: 10.7498/aps.56.4441 [18] 姜振益, 李盛涛. NiTi合金势能面的第一性原理研究. , 2006, 55(11): 6032-6035. doi: 10.7498/aps.55.6032 [19] 韩慧仙, 彭 谦, 文振翼, 王育彬. S2O分子的局域势能面和振动光谱的解析. , 2005, 54(1): 78-84. doi: 10.7498/aps.54.78 [20] 王晓艳, 丁世良. 用李代数方法构造四原子分子的势能面. , 2004, 53(2): 423-426. doi: 10.7498/aps.53.423
下载:
计量
- 文章访问数: 4497
- PDF下载量: 97
- 被引次数: 0
