Numerical investigation of one-dimensional steady detonation wave characteristics for magnesium particle-air mixture

Liu Long; Xia Zhi-Xun; Huang Li-Ya; Ma Li-Kun; Na Xu-Dong

doi:10.7498/aps.68.20190974

Abstract

Magnesium particles have broad application prospects as fuel or additive for detonation combustion power systems due to their high energy density, ignition characteristics and combustion efficiency. In this paper, a one-dimensional steady-state model is established for the magnesium particle-air mixture. The distribution of the flow field and the influences of factors such as phase transition process, inlet velocity, particle radius and initial particle density on the structure of detonation wave are analyzed numerically under different working conditions. The studies have shown that the process accelerating to the sound speed due to the expansion of the gas phase mainly occurs in the pure evaporation reaction stage of the magnesium particles. The duration of magnesium and magnesium oxide melting accounts for a small proportion of the entire combustion process. Under the initial conditions of normal temperature and pressure, the theoretical maximum temperature in the detonation wave during self-sustaining propagation is lower than the dissociation temperature of the magnesium oxide. The heat absorbed in the magnesium melting process is released into the gas phase for expansion work as the reaction progresses, leading to a small effect of magnesium melting on the structure of the detonation wave. The amount of exothermic heat absorbed in the magnesium oxide melting process is so large that the process of expansion of the gaseous working fluid is almost stopped. Moreover, the absorbed heat cannot be used for gas phase expansion work. Therefore, the melting process of magnesium oxide has a great influence on the structure of the detonation wave. The detonation wave of the magnesium particle-air mixture can be stabilized and self-sustained only at the eigenvalue velocity. Below this value, a singular point appears in the flow field. Above this value, the wave cannot be accelerated to the speed of sound, and the downstream flow field disturbance can pass through the reaction combustion zone and weaken the intensity of the detonation wave. When the end of the detonation wave is in the melting process, the detonation wave can still stabilize the self-sustaining propagation when a certain inflow velocity and a magnesium particle density are satisfied. Otherwise, the detonation wave can propagate only at an average speed with oscillation. The initial particle concentration corresponding to the peak of the eigenvalue velocity is smaller than the stoichiometric one corresponding to the peaks of the density, pressure and temperature, indicating that the eigenvalue velocity is not dependent solely on the heat release of the reaction because the interaction between the two phases also affects the conversion efficiency of thermal energy into gas phase kinetic energy. Under the premise of uniform distribution of internal temperature of magnesium particles, the particle size mainly affects the size of the detonation wave, but has little effect on the characteristic value of the eigenvalue velocity and the Chapman-Jouguet parameters. The model in this paper comprehensively reflects the influence of the phase transition process in the combustion process on the structure of the detonation wave and the self-sustaining propagation mechanism. It has a certain guiding significance for designing the detonation power device using powder fuel.

Keywords:

Authors and contacts

1.
Science and Technology on Scramjet Laboratory, College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China
2.
College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China

Corresponding author: Huang Li-Ya, huangliya05@nudt.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 51706241, 11572349)

FullText HTML : translate this paragraph

References

[1]	Wolanski P 2013 Proc. Combust. Inst. 34 125 Google Scholar
[2]	Veyssiere B, Ingignoli W 2003 Shock Waves 12 291 Google Scholar
[3]	Veyssiere B, Bozier O, Khasainov B 2002 Shock Waves 12 227 Google Scholar
[4]	Palaszewski B, Jurns J, Breisacher K, Kearns K 2004 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit Fort Lauderdale, Florida, USA, July 11−14, 2004 p4191
[5]	Bykovskii F A, Zhdan S A, Vedernikov E F, Zholobov Yu A 2010 Dokl. Phys. 55 142 Google Scholar
[6]	Bykovskii F A, Zhdan S A, Vedernikov E F, Zholobov Yu A 2011 Combust. Expl. Shock Waves 47 473 Google Scholar
[7]	Bykovskii F A, Zhdan S A, Vedernikov E F, Zholobov Yu A 2012 Combust. Expl. Shock Waves 48 203 Google Scholar
[8]	Bykovskii F A, Zhdan S A, Vedernikov E F, Zholobov Yu A 2013 Combust. Expl. Shock Waves 49 705 Google Scholar
[9]	Bykovskii F A, Zhdan S A, Vedernikov E F 2014 Combust. Expl. Shock Waves 50 214 Google Scholar
[10]	Lee J H S 1998 The Detonation Phenomenon (New York: Cambridge University Press) p7
[11]	Fedorov A V, Khmel’ T A, Fomin V M 1999 Shock Waves 9 313 Google Scholar
[12]	洪滔 2003 博士学位论文 (北京: 中国工程物理研究院) Hong T 2003 Ph. D. Dissertation (Beijing: China Academy of Engineering Physics) (in Chinese)
[13]	Zhang F 2009 Shock Wave Science and Technology Reference Library (Vol. 4) ( Berlin, Heidelberg: Springer) pp99, 153, 159
[14]	Uphoff U, Hänel D, Roth P 1996 Shock Waves 6 17 Google Scholar
[15]	Fedorov A V, Khmel T A 1999 Combust. Expl. Shock Waves 35 288 Google Scholar
[16]	Benkiewicz K, Hayashi K 2003 Shock Waves 12 385 Google Scholar
[17]	洪滔, 秦承森 2004 爆炸与冲击 24 193 Google Scholar Hong T, Qing C S 2004 Expl. Shock Wave 24 193 Google Scholar
[18]	Fedorov A V, Khmel’ T A 2005 Combust. Expl. Shock Waves 41 78 Google Scholar
[19]	Fedorov A V, Khmel’ T A 2005 Combust. Expl. Shock Waves 41 435 Google Scholar
[20]	Fedorov A V, Khmel’ T A 2008 Combust. Expl. Shock Waves 44 343 Google Scholar
[21]	胡洪波, 翁春生 2011 火箭推进 37 47 Google Scholar Hu H B, Wen C S 2011 J. Rocket Propul. 37 47 Google Scholar
[22]	韦伟, 翁春生 2012 弹道学报 24 99 Google Scholar Wei W, Wen C S 2012 J. Ball 24 99 Google Scholar
[23]	韦伟, 翁春生 2012 南京师范大学学报(工程技术版) 12 53 Google Scholar Wei W, Wen C S 2012 J. Nanjing Normal University (Eng. Technol. Ed.) 12 53 Google Scholar
[24]	韦伟, 翁春生 2015 爆炸与冲击 35 29 Google Scholar Wei W, Wen C S 2015 Expl. Shock Wave 35 29 Google Scholar
[25]	韦伟, 翁春生 2017 固体火箭技术 40 41 Wei W, Wen C S 2017 J. Solid Rock. Technol. 40 41
[26]	昝文涛, 洪滔, 董贺飞 2017 含能材料 25 508 Google Scholar Zan W T, Hong T, Dong H F 2017 Chin. J. Energ. Mater. 25 508 Google Scholar
[27]	Teng H, Jiang Z 2013 Combust. Flame 160 463 Google Scholar
[28]	杨晋朝, 夏智勋, 胡建新 2012 61 164702 Google Scholar Yang J C, Xia Z X, Hu J X 2012 Acta Phys. Sin. 61 164702 Google Scholar
[29]	杨晋朝, 夏智勋, 胡建新 2013 62 074701 Google Scholar Yang J C, Xia Z X, Hu J X 2013 Acta Phys. Sin. 62 074701 Google Scholar
[30]	方丁酉 1988 两相流动力学(长沙: 国防科技大学出版社) 第17页 Fang D J 1988 Two-phase Flow Dynamics (Changsha: National Defense Science and Technology University Press) p17 (in Chinese)
[31]	Steinberg T A, Wilson D, Benz F 1992 Combust. Flame 91 200 Google Scholar
[32]	Kashireninov O E, Kuznetsov V A, Manelis G B 1977 Aiaa J. 15 1035
[33]	Gosteev Y A, Fedorov A V 2005 Combust. Expl. Shock Waves 41 190 Google Scholar
[34]	洪滔, 秦承森 1999 爆炸与冲击 19 335 Google Scholar Hong T, Qing C S 1999 Expl. Shock Wave 19 335 Google Scholar
[35]	Zhang F, Murray S B, Gerrard K B 2004 Proceedings of the 24th International Symposium on Shock Waves Beijing, China, July 11−16, 2004 p795
[36]	杨世铭, 陶文铨 2006 传热学 (第4版) (北京:高等教育出版社) 第121页 Yang S M, Tao W Q 2006 Heat Transfer (4th Ed.) (Beijing: Higher Education Press) p121 (in Chinese)

Cited By

图 1 一维稳态爆震波结构示意图

Figure 1. Schematic of the steady one-dimensionional detonation wave.

DownLoad: Full-Size Img PowerPoint

图 2 不同网格条件下气相密度分布(内插图为局部放大图)

Figure 2. Spatial distribution of the gas-phase density with different grid sizes. Inset shows the view of partial enlargement.

DownLoad: Full-Size Img PowerPoint

图 3 不同来流速度条件下爆震波末端$1 - Ma_1^2$与$\phi $的空间分布

Figure 3. Spatial distribution of $1 - Ma_1^2$ and $\phi $ at the end of detonation wave with different inlet velocity.

DownLoad: Full-Size Img PowerPoint

图 4 爆震波流场参数分布　(a) 密度和质量分数; (b) 速度和压力; (c) 温度

Figure 4. Parameters distribution in detonation wave: (a) Density and mass fraction; (b) velocity and pressure; (c) temperature.

DownLoad: Full-Size Img PowerPoint

图 5 气态工质爆震燃烧过程压力-比体积曲线　(a) Mg熔化; (b) MgO熔化

Figure 5. Pressure-specific volume curve of detonation combustion in gaseous phase:　(a) Mg fusion; (b) MgO fusion.

DownLoad: Full-Size Img PowerPoint

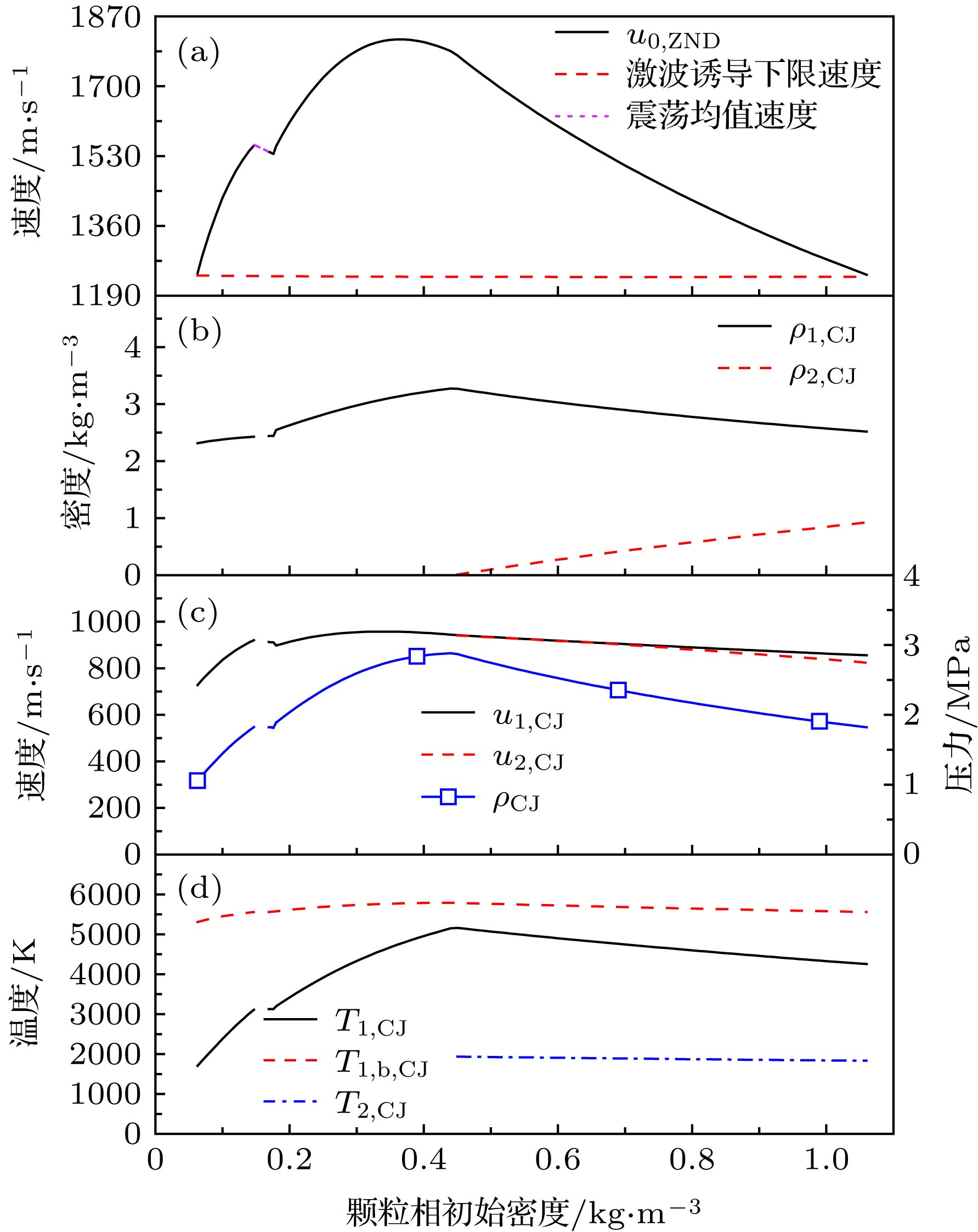
图 6 流场参数随颗粒相初始密度的变化　(a) 特征值速度和激波诱导下限速度; (b) 密度; (c) 速度和压力; (d) 温度

Figure 6. Variation of parameters with different initial concentration of particle phase:　(a) Eigenvalue detonation velocity and minimum velocity of particle ignition induced by shock wave; (b) density; (c) velocity and pressure; (d) temperature.

DownLoad: Full-Size Img PowerPoint

图 7 流场参数随颗粒初始半径的变化　(a)速度; (b)密度和压力; (c)温度; (d)爆震波长度

Figure 7. Variation of parameters with different initial particle radii:　(a) Velocity; (b) density and pressure; (c) temperature; (d) length of detonation wave.

DownLoad: Full-Size Img PowerPoint

表 1 镁和铝的结果对比

Table 1. Comparison of results of magnesium and aluminum detonation.

燃料种类质量热值/MJ·kg^–1 理论空燃比爆震波速度/m·s^–1 CJ面密度/kg·m^–3 CJ面速度/m·s^–1 CJ面压力/MPa

镁 25.06 2.87 1782.28 3.27 942.7 2.87
铝 31.07 3.83 1650 2.43 673 2.04

DownLoad: CSV

表 2 诱导区及相变区长度

Table 2. Length of induction region and phase-transition region.

总长度诱导区燃烧区
(Mg蒸发) Mg
熔化 MgO
熔化 MgO
离解

空间长度/m 0.3324 0.0354 0.297 0.0116 0.0048 ×
占比 1 0.106 0.894 0.035 0.014 ×

DownLoad: CSV

表 3 相变过程对爆震波结构影响对比

Table 3. Effect of phase transition on structure of detonation wave.

$\Delta h_{\rm{Mg},f}$/MJ·kg^–1 $\Delta h_{\rm{MgO},f}$/MJ·kg^–1 $\eta_{0.99\rm{CJ}}$ 燃烧区占比

0.354 1.946 0.995 0.894
0 1.946 0.952 0.885
0.354 0 0.573 0.872
0 0 0.549 0.865

DownLoad: CSV

map

[1]	Wolanski P 2013 Proc. Combust. Inst. 34 125 Google Scholar
[2]	Veyssiere B, Ingignoli W 2003 Shock Waves 12 291 Google Scholar
[3]	Veyssiere B, Bozier O, Khasainov B 2002 Shock Waves 12 227 Google Scholar
[4]	Palaszewski B, Jurns J, Breisacher K, Kearns K 2004 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit Fort Lauderdale, Florida, USA, July 11−14, 2004 p4191
[5]	Bykovskii F A, Zhdan S A, Vedernikov E F, Zholobov Yu A 2010 Dokl. Phys. 55 142 Google Scholar
[6]	Bykovskii F A, Zhdan S A, Vedernikov E F, Zholobov Yu A 2011 Combust. Expl. Shock Waves 47 473 Google Scholar
[7]	Bykovskii F A, Zhdan S A, Vedernikov E F, Zholobov Yu A 2012 Combust. Expl. Shock Waves 48 203 Google Scholar
[8]	Bykovskii F A, Zhdan S A, Vedernikov E F, Zholobov Yu A 2013 Combust. Expl. Shock Waves 49 705 Google Scholar
[9]	Bykovskii F A, Zhdan S A, Vedernikov E F 2014 Combust. Expl. Shock Waves 50 214 Google Scholar
[10]	Lee J H S 1998 The Detonation Phenomenon (New York: Cambridge University Press) p7
[11]	Fedorov A V, Khmel’ T A, Fomin V M 1999 Shock Waves 9 313 Google Scholar
[12]	洪滔 2003 博士学位论文 (北京: 中国工程物理研究院) Hong T 2003 Ph. D. Dissertation (Beijing: China Academy of Engineering Physics) (in Chinese)
[13]	Zhang F 2009 Shock Wave Science and Technology Reference Library (Vol. 4) ( Berlin, Heidelberg: Springer) pp99, 153, 159
[14]	Uphoff U, Hänel D, Roth P 1996 Shock Waves 6 17 Google Scholar
[15]	Fedorov A V, Khmel T A 1999 Combust. Expl. Shock Waves 35 288 Google Scholar
[16]	Benkiewicz K, Hayashi K 2003 Shock Waves 12 385 Google Scholar
[17]	洪滔, 秦承森 2004 爆炸与冲击 24 193 Google Scholar Hong T, Qing C S 2004 Expl. Shock Wave 24 193 Google Scholar
[18]	Fedorov A V, Khmel’ T A 2005 Combust. Expl. Shock Waves 41 78 Google Scholar
[19]	Fedorov A V, Khmel’ T A 2005 Combust. Expl. Shock Waves 41 435 Google Scholar
[20]	Fedorov A V, Khmel’ T A 2008 Combust. Expl. Shock Waves 44 343 Google Scholar
[21]	胡洪波, 翁春生 2011 火箭推进 37 47 Google Scholar Hu H B, Wen C S 2011 J. Rocket Propul. 37 47 Google Scholar
[22]	韦伟, 翁春生 2012 弹道学报 24 99 Google Scholar Wei W, Wen C S 2012 J. Ball 24 99 Google Scholar
[23]	韦伟, 翁春生 2012 南京师范大学学报(工程技术版) 12 53 Google Scholar Wei W, Wen C S 2012 J. Nanjing Normal University (Eng. Technol. Ed.) 12 53 Google Scholar
[24]	韦伟, 翁春生 2015 爆炸与冲击 35 29 Google Scholar Wei W, Wen C S 2015 Expl. Shock Wave 35 29 Google Scholar
[25]	韦伟, 翁春生 2017 固体火箭技术 40 41 Wei W, Wen C S 2017 J. Solid Rock. Technol. 40 41
[26]	昝文涛, 洪滔, 董贺飞 2017 含能材料 25 508 Google Scholar Zan W T, Hong T, Dong H F 2017 Chin. J. Energ. Mater. 25 508 Google Scholar
[27]	Teng H, Jiang Z 2013 Combust. Flame 160 463 Google Scholar
[28]	杨晋朝, 夏智勋, 胡建新 2012 61 164702 Google Scholar Yang J C, Xia Z X, Hu J X 2012 Acta Phys. Sin. 61 164702 Google Scholar
[29]	杨晋朝, 夏智勋, 胡建新 2013 62 074701 Google Scholar Yang J C, Xia Z X, Hu J X 2013 Acta Phys. Sin. 62 074701 Google Scholar
[30]	方丁酉 1988 两相流动力学(长沙: 国防科技大学出版社) 第17页 Fang D J 1988 Two-phase Flow Dynamics (Changsha: National Defense Science and Technology University Press) p17 (in Chinese)
[31]	Steinberg T A, Wilson D, Benz F 1992 Combust. Flame 91 200 Google Scholar
[32]	Kashireninov O E, Kuznetsov V A, Manelis G B 1977 Aiaa J. 15 1035
[33]	Gosteev Y A, Fedorov A V 2005 Combust. Expl. Shock Waves 41 190 Google Scholar
[34]	洪滔, 秦承森 1999 爆炸与冲击 19 335 Google Scholar Hong T, Qing C S 1999 Expl. Shock Wave 19 335 Google Scholar
[35]	Zhang F, Murray S B, Gerrard K B 2004 Proceedings of the 24th International Symposium on Shock Waves Beijing, China, July 11−16, 2004 p795
[36]	杨世铭, 陶文铨 2006 传热学 (第4版) (北京:高等教育出版社) 第121页 Yang S M, Tao W Q 2006 Heat Transfer (4th Ed.) (Beijing: Higher Education Press) p121 (in Chinese)

[1]	Liu Long, Xia Zhi-Xun, Huang Li-Ya, Ma Li-Kun, Chen Bin-Bin. Numerical investigation of one-dimensional unsteady detonation wave characteristics of magnesium particle-air mixture. Acta Physica Sinica, 2020, 69(19): 194701. doi: 10.7498/aps.69.20200549
[2]	Li Shi-Yao, Yu Ming. Thermal nonequilibrium detonation model of solid explosive. Acta Physica Sinica, 2018, 67(21): 214704. doi: 10.7498/aps.67.20172501
[3]	Jiang Yi-Min, Liu Mario. A thermodynamic model of grain-grain contact force. Acta Physica Sinica, 2018, 67(4): 044502. doi: 10.7498/aps.67.20171441
[4]	Liang Xiao, Wang Rui-Li. Sensitivity analysis and validation of detonation computational fluid dynamics model. Acta Physica Sinica, 2017, 66(11): 116401. doi: 10.7498/aps.66.116401
[5]	Li Xiang, Wu De-Wei, Wang Xi, Miao Qiang, Chen Kun, Yang Chun-Yan. A method of evaluating the quality of dual-path entangled quantum microwave signal generated based on von Neumann entropy. Acta Physica Sinica, 2016, 65(11): 114204. doi: 10.7498/aps.65.114204
[6]	Chen Fu-Zhen, Qiang Hong-Fu, Miao Gang, Gao Wei-Ran. Numerical simulation of fuel dispersal into cloud and its combustion and explosion with smoothed discrete particle hydrodynamics. Acta Physica Sinica, 2015, 64(11): 110202. doi: 10.7498/aps.64.110202
[7]	Zhou Hong-Qiang, Yu Ming, Sun Hai-Quan, Dong He-Fei, Zhang Feng-Guo. A continuum constitutive model and computational method of explosive detonation. Acta Physica Sinica, 2014, 63(22): 224702. doi: 10.7498/aps.63.224702
[8]	Yang Chen, Fang Chao, Zhang Jian, Cao Jian-Zhu. Study on cumulative fractional release of radionuclides in HTGR fuel particles. Acta Physica Sinica, 2014, 63(3): 032802. doi: 10.7498/aps.63.032802
[9]	Han Dong, Chen Liang-Fu, Li Shen-Shen, Tao Jin-Hua, Su Lin, Zou Ming-Min, Fan Meng. A convolution algorithm of differential coefficients of liquid water based on vibrational Raman scattering. Acta Physica Sinica, 2013, 62(10): 109301. doi: 10.7498/aps.62.109301
[10]	Yang Jin-Zhao, Xia Zhi-Xun, Hu Jian-Xin. Numerical studies of ignition and combustion of pulverized magnesium particle cloud. Acta Physica Sinica, 2013, 62(7): 074701. doi: 10.7498/aps.62.074701
[11]	Jing Long-Fei, Huang Tian-Xuan, Jiang Shao-En, Chen Bo-Lun, Pu Yu-Dong, Hu Feng, Cheng Shu-Bo. Model analysis of experiments of implosion symmetry on Shenguang-Ⅱ and Shenguang-Ⅲ prototype laser facilities. Acta Physica Sinica, 2012, 61(10): 105205. doi: 10.7498/aps.61.105205
[12]	Wang Hao, Liu Guo-Quan, Luan Jun-Hua. Study on 3D von Neumann equation with anisotropy for convex grains. Acta Physica Sinica, 2012, 61(4): 048102. doi: 10.7498/aps.61.048102
[13]	Fang Chao, Liu Ma-Lin. The study of the Raman spectra of SiC layers in TRISO particles. Acta Physica Sinica, 2012, 61(9): 097802. doi: 10.7498/aps.61.097802
[14]	Yang Jin-Zhao, Xia Zhi-Xun, Hu Jian-Xin. Numerical studies of unsteady ignition of pulverized magnesium particle cloud. Acta Physica Sinica, 2012, 61(16): 164702. doi: 10.7498/aps.61.164702
[15]	Yu Ben-Hai, Liu Mo-Lin, Chen Dong. First principles study of structural, electronic and elastic properties of Mg2 Si polymorphs. Acta Physica Sinica, 2011, 60(8): 087105. doi: 10.7498/aps.60.087105
[16]	Lu Kun-Quan, Hou Mei-Ying, Wang Qiang, Jiang Ze-Hui, Liu Ji-Xing. Propagation, distribution and detection principle of seismic precursory signals. Acta Physica Sinica, 2011, 60(11): 119101. doi: 10.7498/aps.60.119101
[17]	Yang Yi-Tao, Zhang Chong-Hong, Zhou Li-Hong, Li Bing-Sheng, Zhang Li-Qing. Synthesis of metallic nanoparticles in spinel via defects induced by the inert-gas-ion implantation. Acta Physica Sinica, 2009, 58(1): 399-403. doi: 10.7498/aps.58.399
[18]	Guo Shu-Xu, Wang Wei, Shi Jia-Wei. Intermolecular potential energy and band calculation in polymorphs of pentacene. Acta Physica Sinica, 2007, 56(7): 4085-4088. doi: 10.7498/aps.56.4085
[19]	YANG HONG-QIONG, YANG JIAN-LUN, WEN SHU-HUAI, WANG GEN-XING, GUO YU-ZHI, TANG ZHENG-YUAN, MU WEI-BING, MA CHI. DT FUEL AREAL DENSITY DIAGNOSTIC IN DIRECT-DRIVEN IMPLOSIONS. Acta Physica Sinica, 2001, 50(12): 2408-2412. doi: 10.7498/aps.50.2408
[20]	. . Acta Physica Sinica, 1966, 22(9): 1098-1102. doi: 10.7498/aps.22.1098

Catalog

Vol. 68, Issue 24 - 2019-12-20

Metrics

Abstract views: 6822
PDF Downloads: 64
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板