Improved BW model based on MLP neural network optimization

CHEN Cunyu; CHEN Aixi; QI Xiaoqiu; WANG Hankui

doi:10.7498/aps.74.20241201

Abstract

The nuclear mass model has significant applications in nuclear physics, astrophysics, and nuclear engineering. The accurate prediction of binding energy is crucial for studying nuclear structure, reactions, and decay. However, traditional mass models exhibit significant errors in double magic number region and heavy nuclear region. These models are difficult to effectively describe shell effect and parity effect in the nuclear structure, and also fail to capture the subtle differences observed in experimental results. This study demonstrates the powerful modeling capabilities of MLP neural networks, which optimize the parameters of the nuclear mass model, and reduce prediction errors in key regions and globally. In the neural network, neutron number, proton number, and binding energy are used as training feature values, and the mass-model coefficient is regarded as training label value. The training set is composed of the multiple sets of calculated nuclear mass model coefficients. Through extensive experiments, the optimal parameters are determined to ensure the convergence speed and stability of the model. The Adam optimizer is used to adjust the weight and bias of the network to reduce the mean squared error loss during training. Based on the AME2020 dataset, the trained neural network model with the minimum loss is used to predict the optimal coefficients of the nuclear mass model. The optimized BW2 model significantly reduces root-mean-square errors in double magic number and heavy nuclear regions. Specifically, the optimized model reduces the root-mean-square error by about 28%, 12%, and 18% near Z = 50 and N = 50; Z(N) = 50 and N = 82; Z = 82 and N = 126, respectively. In the heavy nuclear region, the error is reduced by 48%. The BW3 model combines higher-order symmetry energy terms, and after parameter optimization using the neural network, reduces the global root-mean-square error from 1.86 MeV to 1.63 MeV. This work reveals that the model with newly optimized coefficients not only exhibit significant error reduction near double magic numbers, but also shows the improvements in binding energy predictions for both neutron-rich and neutron-deficient nuclei. Furthermore, the model shows good improvements in describing parity effects, accurately capturing the differences related to parity in isotopic chains with different proton numbers. This study demonstrates the tremendous potential of MLP neural networks in optimizing the parameters of nuclear mass model and provides a novel method for optimizing parameters in more complex nuclear mass models. In addition, the proposed method is applicable to the nuclear mass models with implicit or nonlinear relationships, providing a new perspective for further developing the nuclear mass models.

Keywords:

Authors and contacts

School of Science, Zhejiang Sci-Tech University, Hangzhou 310018, China

Corresponding author: WANG Hankui, whk2007@163.com

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. U2267205, 12475124, 12175199, 12204412) and the Zhejiang Sci-Tech University Talent Start-up Fund, China (Grant Nos. 22062267-Y, 21062349-Y).

FullText HTML

References

[1]	Lunney D, Pearson J M, Thibault C 2003 Rev. Mod. Phys. 75 1021 Google Scholar
[2]	李涛, 黎春青, 周厚兵, 王宁 2021 70 102101 Google Scholar Li T, Li C Q, Zhou H B, Wang N 2021 Acta Phys. Sin. 70 102101 Google Scholar
[3]	Ramirez E M, Ackermann D, Blaum K, Block M, Droese C, Düllmann C E, Dworschak M, Eibach M, Eliseev S, Haettner E, Herfurth F, Heßberger F P, Hofmann S, Ketelaer J, Marx G, Mazzocco M, Nesterenko D, Novikov Y N, Plaß W R, Rodríguez D, Scheidenberger C, Schweikhard L, Thirolf P G, Weber C 2012 Science 337 1207 Google Scholar
[4]	Horoi M 2013 International Summer School for Advanced Studies Dynamics of Open Nuclear Systems (Predeal12) Predeal, Romania, July 9–20, 2012 p012020
[5]	Wienholtz F, Beck D, Blaum K, Borgmann C, Breitenfeldt M, Cakirli R B, George S, Herfurth F, Holt J D, Kowalska M, Kreim S, Lunney D, Manea V, Menéndez J, Neidherr D, Rosenbusch M, Schweikhard L, Schwenk A, Simonis J, Stanja J, Wolf R N, Zuber K 2013 Nature 498 346 Google Scholar
[6]	Burbidge E M, Burbidge G R, Fowler W A, Hoyle F 1957 Rev. Mod. Phys. 29 547 Google Scholar
[7]	Ye W, Qian Y, Ren Z 2022 Phys. Rev. C 106 024318 Google Scholar
[8]	Bethe H A, Bacher R F 1936 Rev. Mod. Phys. 8 82 Google Scholar
[9]	Weizsäcker C F V 1935 Zeitschrift für Physik 96 431 Google Scholar
[10]	Kirson M W 2008 Nucl. Phys. A 798 29 Google Scholar
[11]	Sorlin O, Porquet M G 2008 Prog. Part. Nucl. Phys. 61 602 Google Scholar
[12]	Ozawa A, Kobayashi T, Suzuki T, Yoshida K, Tanihata I 2000 Phys. Rev. Lett. 84 5493 Google Scholar
[13]	Gherghescu R A, Poenaru D N 2022 Phys. Rev. C 106 034616 Google Scholar
[14]	Björck Å 1990 Handb. Numer. Anal. 1 465 Google Scholar
[15]	Jiang B N 1998 Comput. Methods Appl. Mech. Eng. 152 239 Google Scholar
[16]	Mohammed-Azizi B, Mouloudj H 2022 Int. J. Mod. Phys. C 33 2250076 Google Scholar
[17]	Cao Y, Lu D, Qian Y, Ren Z 2022 Phys. Rev. C 105 034304 Google Scholar
[18]	Huang W, Wang M, Kondev F, Audi G, Naimi S 2021 Chin. Phys. C 45 030002 Google Scholar
[19]	Wang M, Huang W, Kondev F, Audi G, Naimi S 2021 Chin. Phys. C 45 030003 Google Scholar
[20]	Sobiczewski A, Pomorski K 2007 Prog. Part. Nucl. Phys. 58 292 Google Scholar
[21]	Yin X, Shou R, Zhao Y M 2022 Phys. Rev. C 105 064304 Google Scholar
[22]	Wang N, Liu M, Wu X 2010 Phys. Rev. C 81 044322 Google Scholar
[23]	Wu Y C, Feng J W 2018 Wirel. Pers. Commun. 102 1645 Google Scholar
[24]	Popescu M C, Balas V E, Perescu-Popescu L, Mastorakis N 2009 WSEAS Trans. Cir. and Sys. 8 579 Google Scholar
[25]	Xiang C, Ding S, Lee T H 2005 IEEE Trans. Neural Netw. 16 84 Google Scholar
[26]	Pinkus A 1999 Acta Numerica 8 143 Google Scholar
[27]	Sharma A, Gandhi A, Kumar A 2022 Phys. Rev. C 105 L031306 Google Scholar
[28]	Wu X H, Ren Z X, Zhao P W 2022 Phys. Rev. C 105 L031303 Google Scholar
[29]	Gao Z P, Wang Y J, Lü H L, Li Q F, Shen C W, Liu L 2021 Nucl. Sci. Tech. 32 109 Google Scholar
[30]	庞龙刚, 周凯, 王新年 2020 原子核物理评论 37 720 Google Scholar Pang L G, Zhou K, Wang X N 2020 Nucl. Phys. Rev. 37 720 Google Scholar
[31]	Gernoth K A, Clark J W 1995 Neural Networks 8 291 Google Scholar
[32]	Yüksel E, Soydaner D, Bahtiyar H 2021 Int. J. Mod. Phys. E 30 2150017 Google Scholar
[33]	Liu M, Wang N, Deng Y, Wu X 2011 Phys. Rev. C 84 014333 Google Scholar
[34]	Wang N, Liu M 2011 Phys. Rev. C 84 051303 Google Scholar
[35]	Utama R, Piekarewicz J, Prosper H B 2016 Phys. Rev. C 93 014311 Google Scholar
[36]	Utama R, Piekarewicz J 2018 Phys. Rev. C 97 014306 Google Scholar
[37]	Ma C, Zong Y Y, Zhao Y M, Arima A 2020 Phys. Rev. C 102 024330 Google Scholar
[38]	Özdoğan H, Üncü Y, Şekerci M, Kaplan A 2022 Appl. Radiat. Isot. 184 110162 Google Scholar
[39]	Chen X, Ma Q, Alkharobi T 2009 2nd IEEE International Conference on Computer Science and Information Technology Beijing, China, August 8–11, 2009 p291
[40]	Ming X C, Zhang H F, Xu R R, Sun X D, Tian Y, Ge Z G 2022 Nucl. Sci. Tech. 33 48 Google Scholar
[41]	Le X K, Wang N, Jiang X 2023 Nucl. Phys. A 1038 122707 Google Scholar
[42]	Slowik A, Kwasnicka H 2020 Neural Comput. Appl. 32 12363 Google Scholar
[43]	Amine K 2019 Adv. Oper. Res. 2019 8134674 Google Scholar
[44]	Wang D, Tan D, Liu L 2018 Soft Computing 22 387 Google Scholar
[45]	Chen A, Tan H, Zhu Y 2022 2nd International Conference on Applied Mathematics, Modelling, and Intelligent Computing (CAMMIC 2022) Kunming, China, March 25–27, 2022 p1472
[46]	Huang L, Qin J, Zhou Y, Zhu F, Liu L, Shao L 2023 IEEE Trans. Pattern Anal. Mach. Intell. 45 10173 Google Scholar
[47]	Xu X Y, Deng L, Chen A X, Yang H, Jalili A, Wang H K 2024 Nucl. Sci. Tech. 35 91 Google Scholar
[48]	Möller P, Myers W D, Sagawa H, Yoshida S 2012 Phys. Rev. Lett. 108 052501 Google Scholar
[49]	Zhang H F, Wang L H, Yin J P, Chen P H, Zhang H F 2017 J. Phys. G: Nucl. Part. Phys. 44 045110 Google Scholar
[50]	Samyn M, Goriely S, Heenen P H, Pearson J, Tondeur F 2002 Nucl. Phys. A 700 142 Google Scholar
[51]	Moller P, Nix J, Myers W, Swiatecki W 1995 At. Data Nucl. Data Tables 59 185 Google Scholar
[52]	Duflo J, Zuker A 1995 Phys. Rev. C 52 R23 Google Scholar

Cited By

图 1 神经网络优化核质量模型系数框架图(MLP, 多层感知机神经网络; Exp., 实验结合能)

Figure 1. Framework diagram of neural network optimizing nuclear mass model coefficients (MLP, multi-layer perceptron neural network; Exp., experimental binding energy).

DownLoad: Full-Size Img PowerPoint

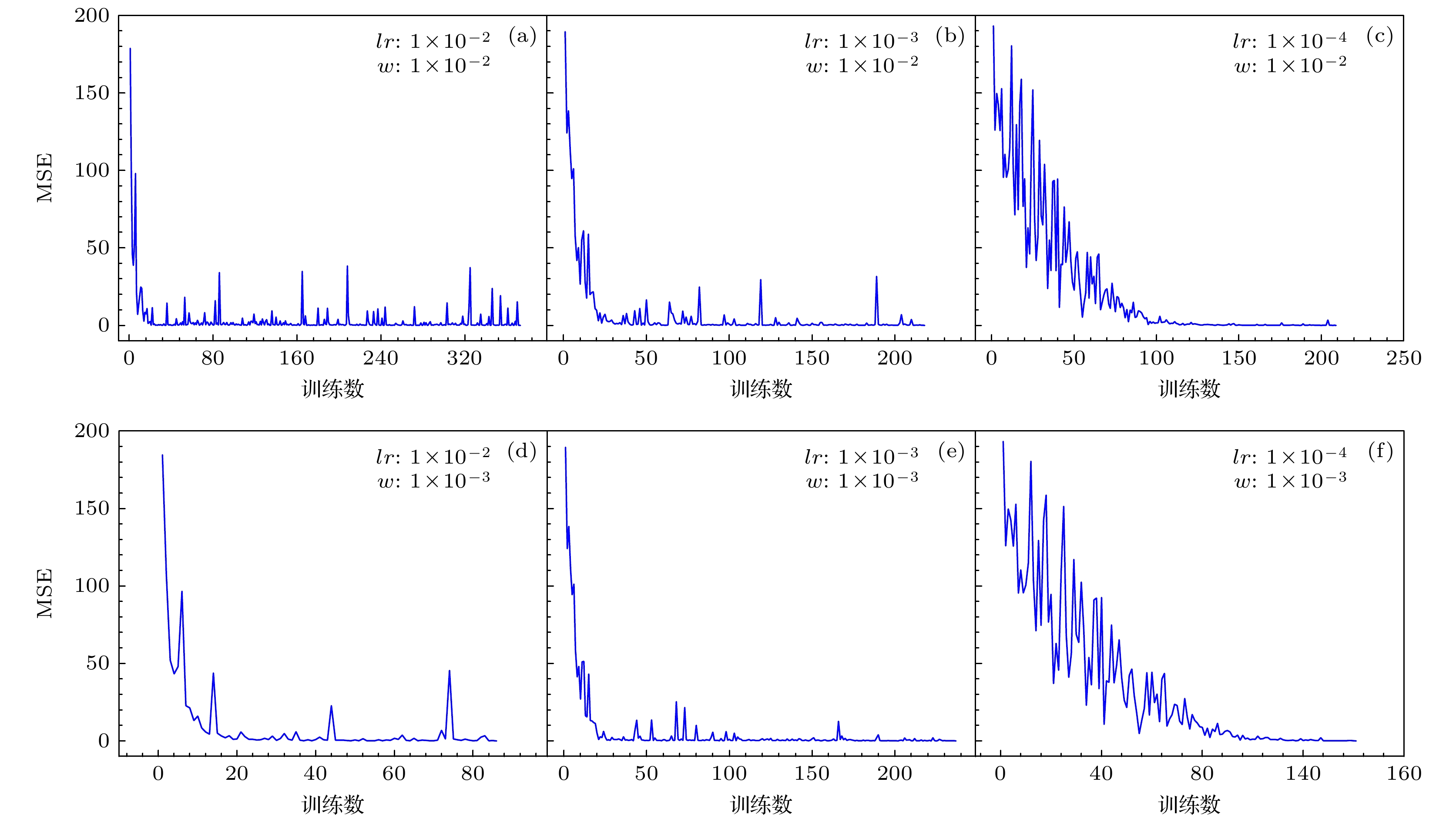
图 2 Adam优化器不同学习率和权重衰减参数实验对比图, 水平坐标为神经网络训练次数, 垂直坐标为神经网络损失值, 当损失值下降低于0.1%时停止训练($ lr $表示学习率, $ w $表示权重衰减参数)

Figure 2. Comparison chart of Adam optimizer with different learning rates and weight decay parameters. The horizontal axis represents the number of neural network training iterations, and the vertical axis represents the neural network loss value. Training stops when the loss value drops below 0.1%. ($ lr $ represents the learning rate, $ w $ represents the weight decay parameter)

DownLoad: Full-Size Img PowerPoint

图 3 BW2质量公式预测值与实验结合能的偏差对比图　(a)初始系数; (b)优化系数

Figure 3. Comparison plot of the deviation of the predicted value of the BW2 mass formula from the experimental binding energy: (a) Original coefficient; (b) optimization coefficient.

DownLoad: Full-Size Img PowerPoint

图 4 随机元素结合能的实验值与质量公式初始系数和优化系数计算值之间的差值折线图

Figure 4. Line plot of the difference between the experimental value of the binding energy of a random element and the calculated value of the original coefficient and optimization coefficient of the mass formula.

DownLoad: Full-Size Img PowerPoint

图 5 相同质量数下对比不同中子数的结合能偏差图

Figure 5. Graph of same mass number vs. different neutron numbers.

DownLoad: Full-Size Img PowerPoint

图 6 中子数相同对比不同质子数的结合能偏差图

Figure 6. Graph of same neutron number vs. differentproton numbers.

DownLoad: Full-Size Img PowerPoint

表 1 MLP神经网络寻找的系数组(部分, 单位: MeV)

Table 1. Coefficients identified by the MLP neural network (partial, unit: MeV).

	1	2	3	4	5	6	7	8
$ \alpha_{v} $	16.58	16.22	16.24	16.21	16.22	16.22	16.24	16.05
$ \alpha_{s} $	–26.95	–23.36	–23.42	–23.39	–23.38	–23.36	–23.40	–23.10
$ \alpha_{C} $	–0.77	–0.74	0.74	–0.74	–0.74	–0.75	–0.75	–0.74
$ \alpha_{t} $	–31.51	–31.53	–31.59	–31.54	–31.57	–31.53	–32.60	–31.62
$ \alpha_{xC} $	2.22	1.39	1.38	1.39	1.40	1.39	1.40	1.59
$ \alpha_{W} $	–43.40	–57.38	–57.40	–57.42	–57.41	–57.40	–57.47	–72.97
$ \alpha_{s t} $	55.62	54.98	55.02	54.96	55.03	54.99	55.09	64.10
$ \alpha_{p} $	9.87	10.63	10.61	10.64	10.64	10.63	10.67	10.56
$ \alpha_{R} $	14.77	9.89	9.94	9.91	9.91	9.89	9.93	9.89
$ \alpha_{m} $	–1.90	–1.89	–1.91	–1.90	–1.89	–1.89	–1.90	–1.88
$ \beta_{m} $	0.14	0.14	0.13	0.14	0.14	0.15	0.15	0.14
$ b $	—	—	—	—	—	—	—	–11.36
$ \sigma $	1.92	1.90	1.84	1.68	1.76	1.81	1.89	1.63

DownLoad: CSV

map

[1]	Lunney D, Pearson J M, Thibault C 2003 Rev. Mod. Phys. 75 1021 Google Scholar
[2]	李涛, 黎春青, 周厚兵, 王宁 2021 70 102101 Google Scholar Li T, Li C Q, Zhou H B, Wang N 2021 Acta Phys. Sin. 70 102101 Google Scholar
[3]	Ramirez E M, Ackermann D, Blaum K, Block M, Droese C, Düllmann C E, Dworschak M, Eibach M, Eliseev S, Haettner E, Herfurth F, Heßberger F P, Hofmann S, Ketelaer J, Marx G, Mazzocco M, Nesterenko D, Novikov Y N, Plaß W R, Rodríguez D, Scheidenberger C, Schweikhard L, Thirolf P G, Weber C 2012 Science 337 1207 Google Scholar
[4]	Horoi M 2013 International Summer School for Advanced Studies Dynamics of Open Nuclear Systems (Predeal12) Predeal, Romania, July 9–20, 2012 p012020
[5]	Wienholtz F, Beck D, Blaum K, Borgmann C, Breitenfeldt M, Cakirli R B, George S, Herfurth F, Holt J D, Kowalska M, Kreim S, Lunney D, Manea V, Menéndez J, Neidherr D, Rosenbusch M, Schweikhard L, Schwenk A, Simonis J, Stanja J, Wolf R N, Zuber K 2013 Nature 498 346 Google Scholar
[6]	Burbidge E M, Burbidge G R, Fowler W A, Hoyle F 1957 Rev. Mod. Phys. 29 547 Google Scholar
[7]	Ye W, Qian Y, Ren Z 2022 Phys. Rev. C 106 024318 Google Scholar
[8]	Bethe H A, Bacher R F 1936 Rev. Mod. Phys. 8 82 Google Scholar
[9]	Weizsäcker C F V 1935 Zeitschrift für Physik 96 431 Google Scholar
[10]	Kirson M W 2008 Nucl. Phys. A 798 29 Google Scholar
[11]	Sorlin O, Porquet M G 2008 Prog. Part. Nucl. Phys. 61 602 Google Scholar
[12]	Ozawa A, Kobayashi T, Suzuki T, Yoshida K, Tanihata I 2000 Phys. Rev. Lett. 84 5493 Google Scholar
[13]	Gherghescu R A, Poenaru D N 2022 Phys. Rev. C 106 034616 Google Scholar
[14]	Björck Å 1990 Handb. Numer. Anal. 1 465 Google Scholar
[15]	Jiang B N 1998 Comput. Methods Appl. Mech. Eng. 152 239 Google Scholar
[16]	Mohammed-Azizi B, Mouloudj H 2022 Int. J. Mod. Phys. C 33 2250076 Google Scholar
[17]	Cao Y, Lu D, Qian Y, Ren Z 2022 Phys. Rev. C 105 034304 Google Scholar
[18]	Huang W, Wang M, Kondev F, Audi G, Naimi S 2021 Chin. Phys. C 45 030002 Google Scholar
[19]	Wang M, Huang W, Kondev F, Audi G, Naimi S 2021 Chin. Phys. C 45 030003 Google Scholar
[20]	Sobiczewski A, Pomorski K 2007 Prog. Part. Nucl. Phys. 58 292 Google Scholar
[21]	Yin X, Shou R, Zhao Y M 2022 Phys. Rev. C 105 064304 Google Scholar
[22]	Wang N, Liu M, Wu X 2010 Phys. Rev. C 81 044322 Google Scholar
[23]	Wu Y C, Feng J W 2018 Wirel. Pers. Commun. 102 1645 Google Scholar
[24]	Popescu M C, Balas V E, Perescu-Popescu L, Mastorakis N 2009 WSEAS Trans. Cir. and Sys. 8 579 Google Scholar
[25]	Xiang C, Ding S, Lee T H 2005 IEEE Trans. Neural Netw. 16 84 Google Scholar
[26]	Pinkus A 1999 Acta Numerica 8 143 Google Scholar
[27]	Sharma A, Gandhi A, Kumar A 2022 Phys. Rev. C 105 L031306 Google Scholar
[28]	Wu X H, Ren Z X, Zhao P W 2022 Phys. Rev. C 105 L031303 Google Scholar
[29]	Gao Z P, Wang Y J, Lü H L, Li Q F, Shen C W, Liu L 2021 Nucl. Sci. Tech. 32 109 Google Scholar
[30]	庞龙刚, 周凯, 王新年 2020 原子核物理评论 37 720 Google Scholar Pang L G, Zhou K, Wang X N 2020 Nucl. Phys. Rev. 37 720 Google Scholar
[31]	Gernoth K A, Clark J W 1995 Neural Networks 8 291 Google Scholar
[32]	Yüksel E, Soydaner D, Bahtiyar H 2021 Int. J. Mod. Phys. E 30 2150017 Google Scholar
[33]	Liu M, Wang N, Deng Y, Wu X 2011 Phys. Rev. C 84 014333 Google Scholar
[34]	Wang N, Liu M 2011 Phys. Rev. C 84 051303 Google Scholar
[35]	Utama R, Piekarewicz J, Prosper H B 2016 Phys. Rev. C 93 014311 Google Scholar
[36]	Utama R, Piekarewicz J 2018 Phys. Rev. C 97 014306 Google Scholar
[37]	Ma C, Zong Y Y, Zhao Y M, Arima A 2020 Phys. Rev. C 102 024330 Google Scholar
[38]	Özdoğan H, Üncü Y, Şekerci M, Kaplan A 2022 Appl. Radiat. Isot. 184 110162 Google Scholar
[39]	Chen X, Ma Q, Alkharobi T 2009 2nd IEEE International Conference on Computer Science and Information Technology Beijing, China, August 8–11, 2009 p291
[40]	Ming X C, Zhang H F, Xu R R, Sun X D, Tian Y, Ge Z G 2022 Nucl. Sci. Tech. 33 48 Google Scholar
[41]	Le X K, Wang N, Jiang X 2023 Nucl. Phys. A 1038 122707 Google Scholar
[42]	Slowik A, Kwasnicka H 2020 Neural Comput. Appl. 32 12363 Google Scholar
[43]	Amine K 2019 Adv. Oper. Res. 2019 8134674 Google Scholar
[44]	Wang D, Tan D, Liu L 2018 Soft Computing 22 387 Google Scholar
[45]	Chen A, Tan H, Zhu Y 2022 2nd International Conference on Applied Mathematics, Modelling, and Intelligent Computing (CAMMIC 2022) Kunming, China, March 25–27, 2022 p1472
[46]	Huang L, Qin J, Zhou Y, Zhu F, Liu L, Shao L 2023 IEEE Trans. Pattern Anal. Mach. Intell. 45 10173 Google Scholar
[47]	Xu X Y, Deng L, Chen A X, Yang H, Jalili A, Wang H K 2024 Nucl. Sci. Tech. 35 91 Google Scholar
[48]	Möller P, Myers W D, Sagawa H, Yoshida S 2012 Phys. Rev. Lett. 108 052501 Google Scholar
[49]	Zhang H F, Wang L H, Yin J P, Chen P H, Zhang H F 2017 J. Phys. G: Nucl. Part. Phys. 44 045110 Google Scholar
[50]	Samyn M, Goriely S, Heenen P H, Pearson J, Tondeur F 2002 Nucl. Phys. A 700 142 Google Scholar
[51]	Moller P, Nix J, Myers W, Swiatecki W 1995 At. Data Nucl. Data Tables 59 185 Google Scholar
[52]	Duflo J, Zuker A 1995 Phys. Rev. C 52 R23 Google Scholar

[1]	TIAN Wenjing, YANG Zongyu, XU Min, LONG Ting, HE Xiaoxue, KE Rui, YANG Shuosu, YU Deliang, SHI Zhongbing, GAO Zheo. Research on Rapid Analysis Model and Extrapolation Method of Neural Network in Spectral Diagnostic. Acta Physica Sinica, 2025, 74(7): . doi: 10.7498/aps.74.20241739
[2]	Tian Shi-Fang, Li Biao. Solving complex nonlinear problems based on gradient-optimized physics-informed neural networks. Acta Physica Sinica, 2023, 72(10): 100202. doi: 10.7498/aps.72.20222381
[3]	Wu Chang-Chun, Zhou Pu-Jun, Wang Jun-Jie, Li Guo, Hu Shao-Gang, Yu Qi, Liu Yang. Memristor based spiking neural network accelerator architecture. Acta Physica Sinica, 2022, 71(14): 148401. doi: 10.7498/aps.71.20220098
[4]	Huang Ying, Gu Chang-Gui, Yang Hui-Jie. Junk-neuron-deletion strategy for hyperparameter optimization of neural networks. Acta Physica Sinica, 2022, 71(16): 160501. doi: 10.7498/aps.71.20220436
[5]	Lou Yue-Shen, Guo Wen-Jun. Prediction of unknown nuclear stability by Bayesian deep neural network. Acta Physica Sinica, 2022, 71(10): 102101. doi: 10.7498/aps.71.20212387
[6]	Wei Lian-Suo, Li Hua, Wu Di, Guo Yuan. Clock synchronization error compensation algorithm based on BP neural network model. Acta Physica Sinica, 2021, 70(11): 114203. doi: 10.7498/aps.70.20201641
[7]	Li Tao, Li Chun-Qing, Zhou Hou-Bing, Wang Ning. Test of nuclear mass models. Acta Physica Sinica, 2021, 70(10): 102101. doi: 10.7498/aps.70.20201734
[8]	Wang Chen-Yang, Duan Qian-Qian, Zhou Kai, Yao Jing, Su Min, Fu Yi-Chao, Ji Jun-Yang, Hong Xin, Liu Xue-Qin, Wang Zhi-Yong. A hybrid model for photovoltaic power prediction of both convolutional and long short-term memory neural networks optimized by genetic algorithm. Acta Physica Sinica, 2020, 69(10): 100701. doi: 10.7498/aps.69.20191935
[9]	Peng Xiang-Kai, Ji Jing-Wei, Li Lin, Ren Wei, Xiang Jing-Feng, Liu Kang-Kang, Cheng He-Nan, Zhang Zhen, Qu Qiu-Zhi, Li Tang, Liu Liang, Lü De-Sheng. Online learning method based on artificial neural network to optimize magnetic shielding characteristic parameters. Acta Physica Sinica, 2019, 68(13): 130701. doi: 10.7498/aps.68.20190234
[10]	Yuan Lin, Yang Xue-Song, Wang Bing-Zhong. Prediction of time reversal channel with neural network optimized by empirical knowledge based genetic algorithm. Acta Physica Sinica, 2019, 68(17): 170503. doi: 10.7498/aps.68.20190327
[11]	Guo Ye-Cai, Zhou Lin-Feng. Study of anisotropic diffusion model based on pulse coupled neural network and image entropy. Acta Physica Sinica, 2015, 64(19): 194204. doi: 10.7498/aps.64.194204
[12]	Li Rui-Guo, Zhang Hong-Li, Fan Wen-Hui, Wang Ya. Hermite orthogonal basis neural network based on improved teaching-learning-based optimization algorithm for chaotic time series prediction. Acta Physica Sinica, 2015, 64(20): 200506. doi: 10.7498/aps.64.200506
[13]	Li Cheng, Shi Dan, Zou Yun-Ping. A feedback neural network with weights of sinusoidal functions. Acta Physica Sinica, 2012, 61(7): 070701. doi: 10.7498/aps.61.070701
[14]	Li Pan-Chi, Wang Hai-Ying, Dai Qing, Xiao Hong. Quantum process neural networks model algorithm and applications. Acta Physica Sinica, 2012, 61(16): 160303. doi: 10.7498/aps.61.160303
[15]	Zhi Qi-Jun. The study of shape and shape-coexistence of neutron rich nuclei around N=28. Acta Physica Sinica, 2011, 60(5): 052101. doi: 10.7498/aps.60.052101
[16]	Ding Bin-Gang, Zhang Da-Li, Lu Ding-Hui. A systematic study on nuclear pairing energy under the relativistic mean-field model. Acta Physica Sinica, 2009, 58(9): 6086-6090. doi: 10.7498/aps.58.6086
[17]	Zheng Hong-Yu, Luo Xiao-Shu, Wu Lei. Excitement and optimality properties of small-world biological neural networks with updated weights. Acta Physica Sinica, 2008, 57(6): 3380-3384. doi: 10.7498/aps.57.3380
[18]	Sheng Zong-Qiang, Guo Jian-You. Systematic investigation of shape-coexistence in Se,Kr,Sr and Zr isotopes with relativistic mean field theory. Acta Physica Sinica, 2008, 57(3): 1557-1563. doi: 10.7498/aps.57.1557
[19]	. The disappearance of conventional magic numbers and the appearance of new numbers near drip-line region studied using relativistic mean-field plus BCS model. Acta Physica Sinica, 2007, 56(12): 6905-6910. doi: 10.7498/aps.56.6905
[20]	MA YU-QIANG, ZHANG YUE-MING, GONG CHANG-DE. RETRIEVAL PROPERTIES OF HOPFIELD NEURAL NETWORK MODELS. Acta Physica Sinica, 1993, 42(8): 1356-1360. doi: 10.7498/aps.42.1356

Catalog

Vol. 74, Issue 1 - 2025-01-05

Metrics

Abstract views: 793
PDF Downloads: 24
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板