Test of nuclear mass models

Li Tao; Li Chun-Qing; Zhou Hou-Bing; Wang Ning

doi:10.7498/aps.70.20201734

Abstract

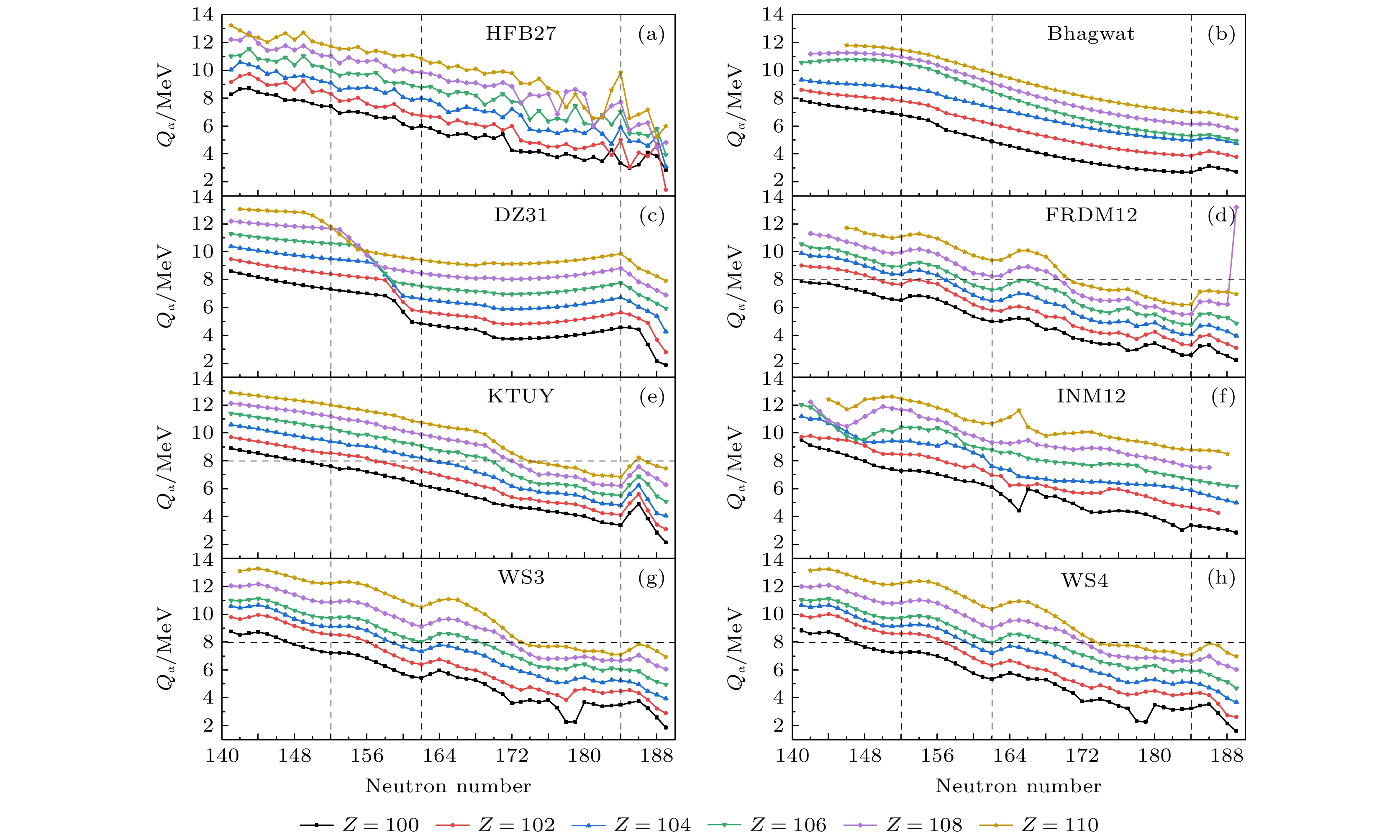
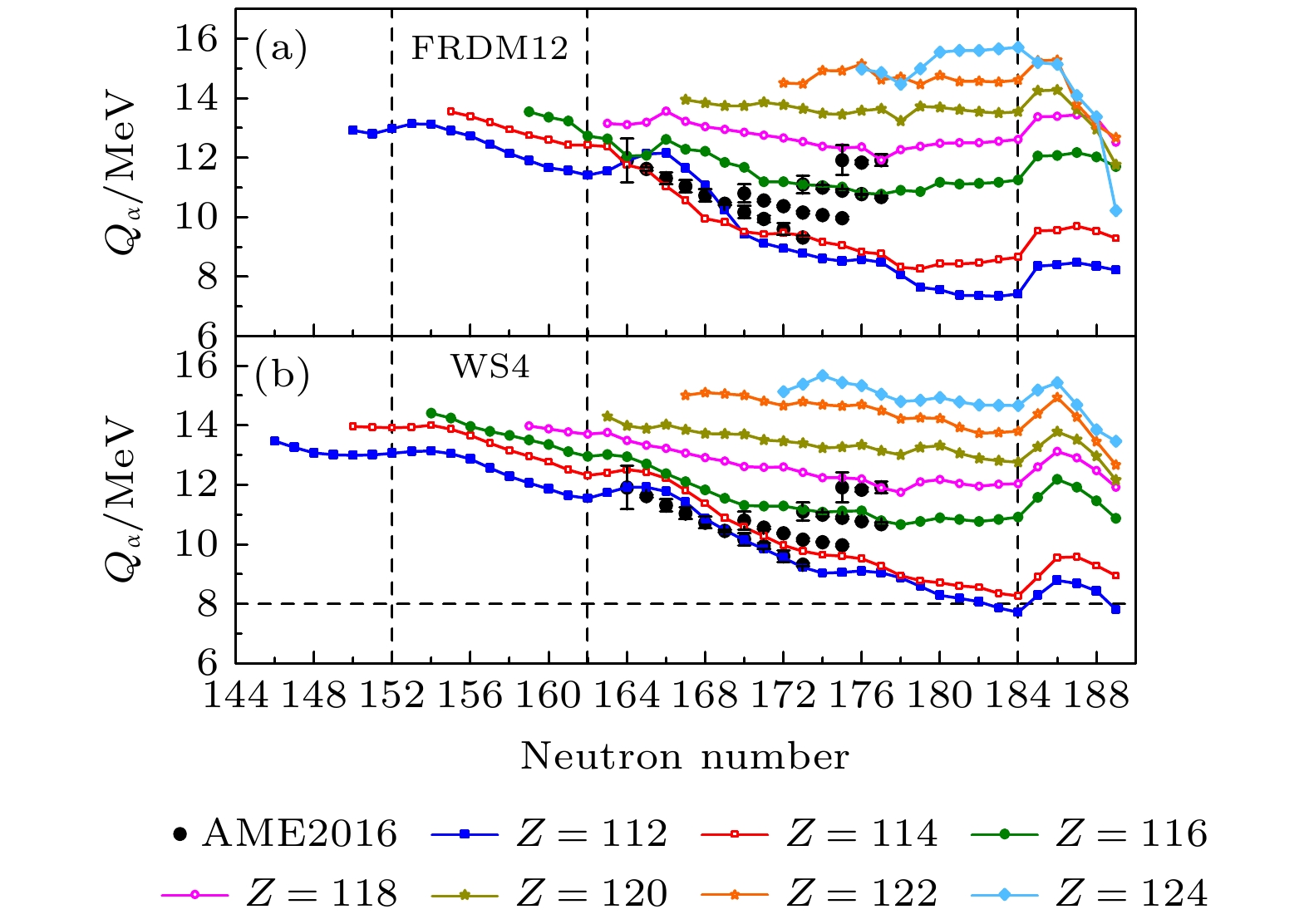
The reliability and prediction ability of 8 global nuclear mass models is systematically analyzed in terms of the accuracy of the model and the new neutron magic number predicted by experiments based on the ground-state nuclear mass data from AME2016. The root-mean-square (RMS) deviations of nuclear mass predicted by 8 nuclear mass models are calculated by subregion, and find that the Bhagwat and WS4 models possess better accuracy to describe the existing experimental data. By analyzing the trend of the neutron shell energy gap varying with neutron number, it is found that the KTUY, WS3 and WS4 models can well represent the mutation behavior caused by the new magic number N = 32, and it is predicted that N = 32 is likely to be a new magic number in the Cl isotope chain and Ar isotope chain. By analyzing the variation trend of α decay energy in the superheavy region, it is found that the FRDM12, WS3 and WS4 models can reproduce the phenomena of subshell with N = 152 and N = 162 well, and predict the relatively long life of nuclei at the neutron number N = 184 for the isotope chain with proton number Z = 108—114. The comprehensive analysis shows that the mass model with good accuracy cannot reproduce shell evolution behavior. For example, the Bhagwat model has the same accuracy as the WS4 model, but it cannot reproduce the mutation behavior of the new magic number N = 32, 152 and 162. But the KTUY model and FRDM12 model can reproduce the new magic number behavior of N = 32, 152 and 162, respectively, although the RMS deviation is slightly larger. The RMS deviation of WS4 model is small and can describe the shell evolution behavior in the nuclear mass well.

Keywords:

Authors and contacts

1.
College of Physical Science and Technology, Guangxi Normal University, Guilin 541004, China
2.
Guangxi Key Laboratory of Nuclear Physics and Technology, Guilin 541004, China

Corresponding author: Li Tao, litao@gxnu.edu.cn

Funds: Project supported by the Joint Funds of the National Natural Science Foundation of China (Grant No. U1867212), the National Natural Science Foundation of China (Grant Nos. 11965003, 11505035, 11675266), the Natural Science Foundation of Guangxi (Grant Nos. 2017GXNSFAA198160, 2017GXNSFGA198001), and the Basic Scientific Research Ability of Young and Middle-aged Teachers in Guangxi Colleges and Universities, China (Grant No. 2019KY0061)

FullText HTML

References

[1]	Roubin A, Atanasov D, Blaum K, George S, Herfurth F, Kisler D, Kowalska M, Kreim S, Lunney D, Manea V, Minaya Ramirez E, Mougeot M, Neidherr D, Rosenbusch M, Schweikhard L, Welker A, Wienholtz F, Wolf R N, Zuber K 2017 Phys. Rev. C 96 014310 Google Scholar
[2]	Wang N, Liu M, Wu X Z 2010 Phys. Rev. C 81 044322 Google Scholar
[3]	Wang Y Z, Gao Y H, Cui J P, Gu J Z 2020 Commun. Theor. Phys. 72 025303 Google Scholar
[4]	Mo Q H, Liu M, Wang N 2014 Phys. Rev. C 90 024320 Google Scholar
[5]	Xu X, Wang M, Zhang Y H, Xu H S, Shuai P, Tu X L, Yuri A L, Zhou X H, Sun B H, Yuan Y J, Xia J W, Yang J C, Klaus B, Chen R J, Chen X C, Fu C Y, Ge Z, Hu Z G, Huang W J, Liu D W, Lan Y H, Ma X W, Mao R S, Uesaka T, Xiao G Q, Xing Y M, Yamaguchi T, Yamaguchi Y, Zeng Q, Yan X L, Zhao H W, Zhao T C, Zhang W, Zhan W L 2015 Chin. Phys. C 39 104001 Google Scholar
[6]	Rosenbusch M, Ascher P, Atanasov D, Barbieri C, Beck D, Blaum K, Borgmann C, Breitenfeldt M, Cakirli R B, Cipollone A, George S, Herfurth F, Kowalska M, Kreim S, Lunney D, Manea V, Navrátil P, Neidherr D, Schweikhard L, Somà V, Stanja J, Wienholtz, F, Wolf R N, Zuber K 2015 Phys. Rev. Lett. 114 202501 Google Scholar
[7]	Reiter M P, Ayet San Andrés S, Dunling E, Kootte B, Leistenschneider E, Andreoiu C, Babcock C, Barquest B R, Bollig J, Brunner T, Dillmann I, Finlay A, Gwinner G, Graham L, Holt J D, Hornung C, Jesch C, Klawitter R, Lan Y, Lascar D, McKay J E, Paul S F, Steinbrügge R, Thompson R, Tracy J L, Jr, Wieser M E, Will C, Dickel T, Plaß W R, Scheidenberger C, Kwiatkowski A A, Dilling J 2018 Phys. Rev. C 98 024310 Google Scholar
[8]	Leistenschneider E, Reiter M P, Ayet San Andrés S, Kootte B, Holt J D, Navrátil P, Babcock C, Barbieri C, Barquest B R, Bergmann J, Bollig J, Brunner T, Dunling E, Finlay A, Geissel H, Graham L, Greiner F, Hergert H, Hornung C, Jesch C, Klawitter R, Lan Y, Lascar D, Leach K G, Lippert W, McKay J E, Paul S F, Schwenk A, Short D, Simonis J, Somà V, Steinbrügge R, Stroberg S R, Thompson R, Wieser M E, Will C, Yavor M, Andreoiu C, Dickel T, Dillmann I, Gwinner G, Plaß W R, Scheidenberger C, Kwiatkowski A A, Dilling J 2018 Phys. Rev. Lett. 120 062503 Google Scholar
[9]	Michimasa S, Kobayashi M, Kiyokawa Y, Ota S, Ahn D S, Baba H, Berg G P A, Dozono M, Fukuda N, Furuno T, Ideguchi E, Inabe N, Kawabata T, Kawase S Kisamori K, Kobayashi K, Kubo T, Kubota Y, Lee C S, Matsushita M, Miya H, Mizukami A, Nagakura H, Nishimura D, Oikawa H, Sakai H, Shimizu Y, Stolz A, Suzuki H, Takaki M, Takeda H, Takeuchi S, Tokieda H, Uesaka T, Yako K, Yamaguchi Y, Yanagisawa Y, Yokoyama R, Yoshida K, Shimoura S 2018 Phys. Rev. Lett. 121 022506 Google Scholar
[10]	Mougeot M, Atanasov D, Blaum K, Chrysalidis K, Goodacre T D, Fedorov D, Fedosseev V, George S, Herfurth F, Holt J D, Lunney D, Manea V, Marsh B, Neidherr D, Rosenbusch M, Rothe S, Schweikhard L, Schwenk A, Seiffert C, Simonis J, Stroberg S R, Welker A, Wienholtz F, Wolf R N, Zuber K 2018 Phys. Rev. Lett. 120 232501 Google Scholar
[11]	Manea V, Karthein J, Atanasov D, Bender M, Blaum K, Cocolios T E, Eliseev S, Herlert A, Holt J D, Huang W J, Litvinov Y A, Lunney D, Menéndez J, Mougeot M, Neidherr D, Schweikhard L, Schwenk A, Simonis J, Welker A, Wienholtz F, Zuber K 2020 Phys. Rev. Lett. 124 092502 Google Scholar
[12]	Erler J, Birge N, Kortelainen M, Nazarewicz W, Olsen E, Perhac A M, Stoitsov M 2012 Nature 486 509 Google Scholar
[13]	Ramirez E M, Ackermann D, Blaum K, Block M, Droese C, Düllmann C E, Dworschak M, Eibach M, Eliseev S, Haettner E, Herfurth F, Heßberger F P, Hofmann S, Ketelaer J, Marx G, Mazzocco M, Nesterenko D, Novikov Y N, Plaß W R, Rodríguez D, Scheidenberger C, Schweikhard L, Thirolf P G, Weber C 2012 Science 337 1207 Google Scholar
[14]	Hamilton J H, Hofmann S, Oganessian Y T 2013 Annu. Rev. Nucl. Part. Sci. 63 383 Google Scholar
[15]	周善贵 2014 物理 43 817 Google Scholar Zhou S G 2014 Physics 43 817 Google Scholar
[16]	周善贵 2017 原子核物理评论 34 318 Google Scholar Zhou S G 2017 Nucl. Phys. Rev. 34 318 Google Scholar
[17]	Li P C, Zhang H F, Wang Y J 2017 Chin. Phys. C 41 114103 Google Scholar
[18]	Düllmann C E, Block M 2018 Sci. Am. 318 46 Google Scholar
[19]	Nazarewicz W 2018 Nat. Phys. 14 537 Google Scholar
[20]	李竹, 牛中明, 孙保华, 王宁, 孟杰 2012 61 072601 Google Scholar Li Z, Niu Z M, Sun B H, Wang N, Meng J 2012 Acta Phys. Sin. 61 072601 Google Scholar
[21]	何建军, 周小红, 张玉虎 2013 物理 42 484 He J J, Zhou X H, Zhang Y H 2013 Physics 42 484
[22]	李竹, 孙保华, 孟杰 2013 物理 42 505 Li Z, Sun B H, Meng J 2013 Physics 42 505
[23]	Niu Z M, Niu Y F, Liang H Z, Long W H, Nikšic T, Vretenar D, Meng J 2013 Phys. Lett. B 723 172 Google Scholar
[24]	Ma C, Li Z, Niu Z M, Liang H Z 2019 Phys. Rev. C 100 024330 Google Scholar
[25]	Li Z, Miu Z M, Sun B H 2019 Sci. China, Ser. G 62 982011 Google Scholar
[26]	唐晓东, 李阔昂 2019 物理 48 633 Google Scholar Tang X D, Li K A 2019 Physics 48 633 Google Scholar
[27]	Möler P, Mumpower M R, Kawano T, Myers W D 2019 At. Data Nucl. Data Tables 125 1 Google Scholar
[28]	王猛, 张玉虎, 周小红 2020 中国科学: 物理学力学天文学 50 052006 Google Scholar Wang M, Zhang Y H, Zhou X H 2020 Sci. Sin.Phys. Mech. Astron. 50 052006 Google Scholar
[29]	Wang M, Audi G, Kondev F G, Huang W J, Naimi S, Xu X 2017 Chin. Phys. C 41 030003 Google Scholar
[30]	Möler P, Sierk A J, Ichikawa T, Sagawa H 2016 At. Data Nucl. Data Tables 109-110 1 Google Scholar
[31]	Koura H, Tachibana T, Uno M, Yamada M 2005 Prog. Theor. Phys. 113 305 Google Scholar
[32]	Wang N, Liang Z Y, Liu M, Wu X Z 2010 Phys. Rev. C 82 044304 Google Scholar
[33]	Liu M, Wang N, Deng Y G, Wu X Z 2011 Phys. Rev. C 84 014333 Google Scholar
[34]	Wang N, Liu M, Wu X Z, Meng J 2014 Phys. Lett. B 734 215 Google Scholar
[35]	Bhagwat A 2014 Phys. Rev. C 90 064306 Google Scholar
[36]	Goriely S, Chamel N, Pearson J M 2013 Phys. Rev. C 88 024308 Google Scholar
[37]	Goriely S, Chamel N, Pearson J M 2013 Phys. Rev. C 88 061302(R Google Scholar
[38]	Goriely S, Chamel N, Pearson J M 2016 Phys. Rev. C 93 034337 Google Scholar
[39]	Geng L S, Toki H, Meng J 2005 Prog. Theor. Phys. 113 785 Google Scholar
[40]	Xia X W, Lim Y, Zhao P W, Liang H Z, Qu X Y, Chen Y, Liu H, Zhang L F, Zhang S Q, Kim Y, Meng J 2018 At. Data Nucl. Data Tables 121-122 1 Google Scholar
[41]	Duflo J, Zuker A P 1995 Phys. Rev. C 52 R23(R Google Scholar
[42]	Zuker A P 2008 Rev. Mex. Fís. 54 129
[43]	Nayak R C, Satpathy L 2012 At. Data Nucl. Data Tables 98 616 Google Scholar
[44]	Sobiczewski A, Litvinov Y A 2014 Phys. Rev. C 89 024311 Google Scholar
[45]	Sobiczewski A, Litvinov Y A 2014 Phys. Rev. C 90 017302 Google Scholar
[46]	Sobiczewski A, Litvinov Y A, Palczewski M 2018 At. Data Nucl. Data Tables 119 1 Google Scholar
[47]	Zheng J S, Wang N Y, Wang Z Y, Niu Z M, Niu Y F, Sun B H 2014 Phys. Rev. C 90 014303 Google Scholar
[48]	Hua X M, Heng T H, Niu Z M, Sun B H, Guo J Y 2012 Sci. China, Ser. G 55 2414 Google Scholar
[49]	Niu Z M, Fang J Y, Niu Y F 2019 Phys. Rev. C 100 054311 Google Scholar

Cited By

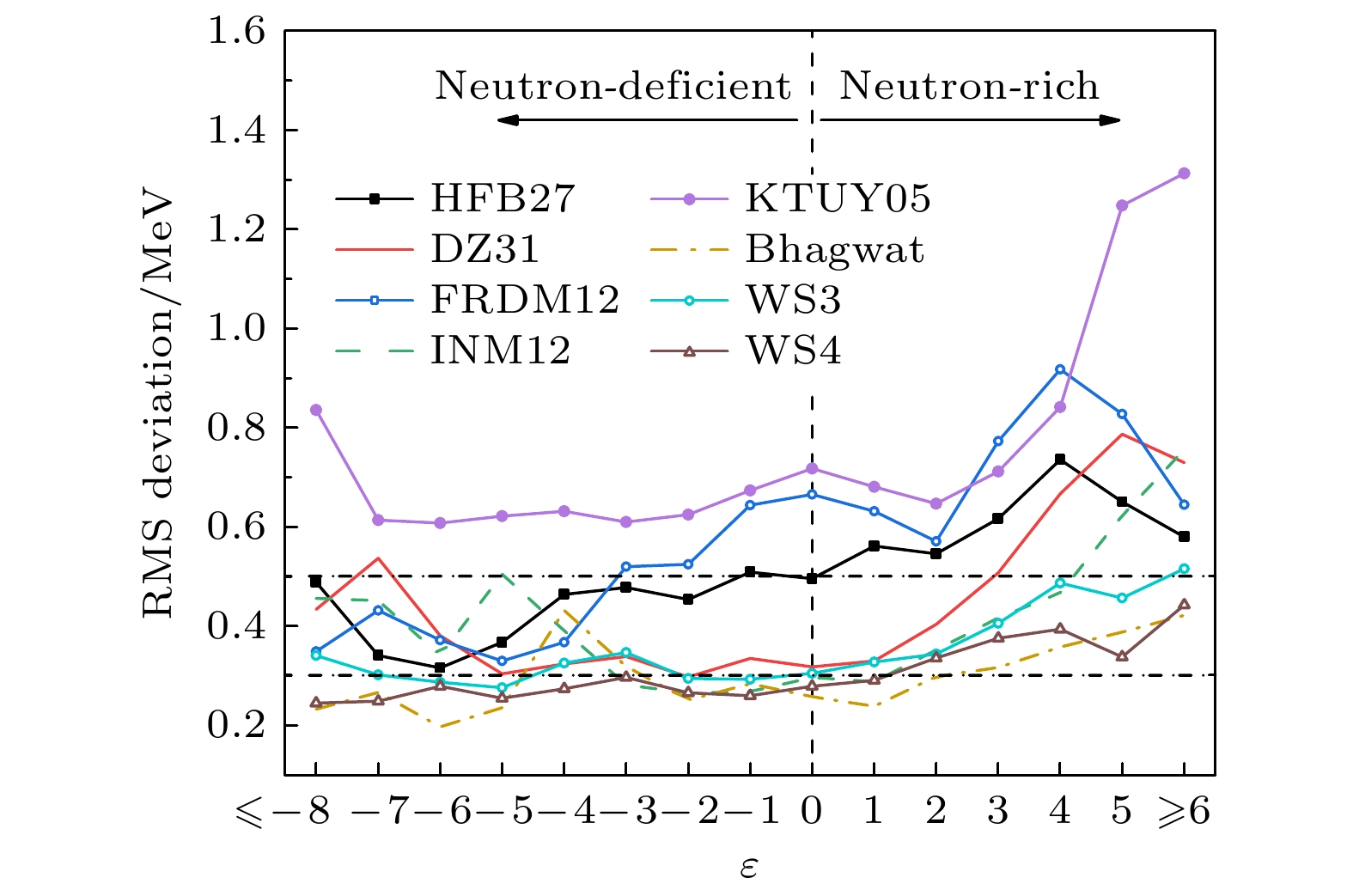
图 1 八个核质量模型对轻核(8 ≤ Z < 28)、中等-I(28 ≤ Z < 50)、中等-II(50 ≤ Z < 82)、重核(82 ≤ Z < 100)以及超重(Z ≥ 100>)五个区域质量描述的均方根偏差

Figure 1. Root-mean-square deviations of the mass of light (8 ≤ Z < 28), medium-I (28 ≤ Z < 50), medium-II (50 ≤ Z < 82), heavy (82 ≤ Z < 100), and super-heavy (Z ≥ 100) are calculated by the 8 nuclear mass models.

DownLoad: Full-Size Img PowerPoint

图 2 八个核质量模型的理论值与实验值的均方根偏差随ε的变化趋势

Figure 2. Root-mean-square deviation between the predictions of the 8 nuclear mass models and the experimental values varies with the ε.

DownLoad: Full-Size Img PowerPoint

图 3 K, Ca, Sc, Ti和V同位素链的中子壳能隙随中子数的变化趋势

Figure 3. Variation trend of neutron shell gaps in K, Ca, Sc, Ti and V isotope chains with neutron number.

DownLoad: Full-Size Img PowerPoint

图 4 八个核质量模型计算的K, Ca, Sc, Ti和V同位素链的中子壳能隙随中子数的变化趋势

Figure 4. Neutron shell gaps of K, Ca, Sc, Ti and V isotopic chains calculated by 8 nuclear mass models vary with the neutron number

DownLoad: Full-Size Img PowerPoint

图 5 Cl和Ar同位素链中子壳能隙随中子数的变化趋势, 竖线表示误差

Figure 5. Variation trend of neutron shell gaps of Cl and Ar isotope chains with neutron number, the vertical bar represents the error.

DownLoad: Full-Size Img PowerPoint

图 6 质子数$ Z=100-110 $为偶数同位素链的α衰变能随中子数的变化趋势

Figure 6. Alpha decay energy of even isotope chains for the proton number $ Z=100-110 $ vary with the neutron number.

DownLoad: Full-Size Img PowerPoint

图 7 八个核质量模型计算的质子数$ Z=100-110 $为偶数同位素链的α衰变能随中子数的变化趋势

Figure 7. Alpha decay energy of even isotope chains for the proton number Z = 100-110 calculated by 8 nuclear mass models vary with the neutron number.

DownLoad: Full-Size Img PowerPoint

图 8 FRDM12和WS4模型计算的质子数$Z=112- $$ 124$为偶数同位素链的α衰变能随中子数的变化趋势, 竖线表示误差

Figure 8. Alpha decay energy of even isotope chains for the proton number Z = 100–110 calculated by the FRDM12 and WS4 models vary with the neutron number, the vertical bar represents the error.

DownLoad: Full-Size Img PowerPoint

表 1 八个核质量模型的基态质量、单中子分离能、单质子分离能、双中子分离能及双质子分离能的均方根偏差

Table 1. Root-mean-square deviations of the ground state mass, single-neutron separation energy, single-proton separation energy, two-neutron separation energy and two-proton separation energy of the 8 nuclear mass models.

模型	M/MeV	S_n/MeV	S_p/MeV	S_2n/MeV	S_2p/MeV
KTUY	0.724	0.306	0.367	0.383	0.527
FRDM12	0.599	0.351	0.368	0.455	0.469
HFB27	0.517	0.424	0.446	0.423	0.464
DZ31	0.422	0.290	0.307	0.342	0.379
INM12	0.381	0.372	0.369	0.375	0.386
WS3	0.343	0.274	0.302	0.296	0.358
WS4	0.302	0.260	0.278	0.276	0.326
Bhagwat	0.301	0.282	0.296	0.306	0.329

DownLoad: CSV

map

[1]	Roubin A, Atanasov D, Blaum K, George S, Herfurth F, Kisler D, Kowalska M, Kreim S, Lunney D, Manea V, Minaya Ramirez E, Mougeot M, Neidherr D, Rosenbusch M, Schweikhard L, Welker A, Wienholtz F, Wolf R N, Zuber K 2017 Phys. Rev. C 96 014310 Google Scholar
[2]	Wang N, Liu M, Wu X Z 2010 Phys. Rev. C 81 044322 Google Scholar
[3]	Wang Y Z, Gao Y H, Cui J P, Gu J Z 2020 Commun. Theor. Phys. 72 025303 Google Scholar
[4]	Mo Q H, Liu M, Wang N 2014 Phys. Rev. C 90 024320 Google Scholar
[5]	Xu X, Wang M, Zhang Y H, Xu H S, Shuai P, Tu X L, Yuri A L, Zhou X H, Sun B H, Yuan Y J, Xia J W, Yang J C, Klaus B, Chen R J, Chen X C, Fu C Y, Ge Z, Hu Z G, Huang W J, Liu D W, Lan Y H, Ma X W, Mao R S, Uesaka T, Xiao G Q, Xing Y M, Yamaguchi T, Yamaguchi Y, Zeng Q, Yan X L, Zhao H W, Zhao T C, Zhang W, Zhan W L 2015 Chin. Phys. C 39 104001 Google Scholar
[6]	Rosenbusch M, Ascher P, Atanasov D, Barbieri C, Beck D, Blaum K, Borgmann C, Breitenfeldt M, Cakirli R B, Cipollone A, George S, Herfurth F, Kowalska M, Kreim S, Lunney D, Manea V, Navrátil P, Neidherr D, Schweikhard L, Somà V, Stanja J, Wienholtz, F, Wolf R N, Zuber K 2015 Phys. Rev. Lett. 114 202501 Google Scholar
[7]	Reiter M P, Ayet San Andrés S, Dunling E, Kootte B, Leistenschneider E, Andreoiu C, Babcock C, Barquest B R, Bollig J, Brunner T, Dillmann I, Finlay A, Gwinner G, Graham L, Holt J D, Hornung C, Jesch C, Klawitter R, Lan Y, Lascar D, McKay J E, Paul S F, Steinbrügge R, Thompson R, Tracy J L, Jr, Wieser M E, Will C, Dickel T, Plaß W R, Scheidenberger C, Kwiatkowski A A, Dilling J 2018 Phys. Rev. C 98 024310 Google Scholar
[8]	Leistenschneider E, Reiter M P, Ayet San Andrés S, Kootte B, Holt J D, Navrátil P, Babcock C, Barbieri C, Barquest B R, Bergmann J, Bollig J, Brunner T, Dunling E, Finlay A, Geissel H, Graham L, Greiner F, Hergert H, Hornung C, Jesch C, Klawitter R, Lan Y, Lascar D, Leach K G, Lippert W, McKay J E, Paul S F, Schwenk A, Short D, Simonis J, Somà V, Steinbrügge R, Stroberg S R, Thompson R, Wieser M E, Will C, Yavor M, Andreoiu C, Dickel T, Dillmann I, Gwinner G, Plaß W R, Scheidenberger C, Kwiatkowski A A, Dilling J 2018 Phys. Rev. Lett. 120 062503 Google Scholar
[9]	Michimasa S, Kobayashi M, Kiyokawa Y, Ota S, Ahn D S, Baba H, Berg G P A, Dozono M, Fukuda N, Furuno T, Ideguchi E, Inabe N, Kawabata T, Kawase S Kisamori K, Kobayashi K, Kubo T, Kubota Y, Lee C S, Matsushita M, Miya H, Mizukami A, Nagakura H, Nishimura D, Oikawa H, Sakai H, Shimizu Y, Stolz A, Suzuki H, Takaki M, Takeda H, Takeuchi S, Tokieda H, Uesaka T, Yako K, Yamaguchi Y, Yanagisawa Y, Yokoyama R, Yoshida K, Shimoura S 2018 Phys. Rev. Lett. 121 022506 Google Scholar
[10]	Mougeot M, Atanasov D, Blaum K, Chrysalidis K, Goodacre T D, Fedorov D, Fedosseev V, George S, Herfurth F, Holt J D, Lunney D, Manea V, Marsh B, Neidherr D, Rosenbusch M, Rothe S, Schweikhard L, Schwenk A, Seiffert C, Simonis J, Stroberg S R, Welker A, Wienholtz F, Wolf R N, Zuber K 2018 Phys. Rev. Lett. 120 232501 Google Scholar
[11]	Manea V, Karthein J, Atanasov D, Bender M, Blaum K, Cocolios T E, Eliseev S, Herlert A, Holt J D, Huang W J, Litvinov Y A, Lunney D, Menéndez J, Mougeot M, Neidherr D, Schweikhard L, Schwenk A, Simonis J, Welker A, Wienholtz F, Zuber K 2020 Phys. Rev. Lett. 124 092502 Google Scholar
[12]	Erler J, Birge N, Kortelainen M, Nazarewicz W, Olsen E, Perhac A M, Stoitsov M 2012 Nature 486 509 Google Scholar
[13]	Ramirez E M, Ackermann D, Blaum K, Block M, Droese C, Düllmann C E, Dworschak M, Eibach M, Eliseev S, Haettner E, Herfurth F, Heßberger F P, Hofmann S, Ketelaer J, Marx G, Mazzocco M, Nesterenko D, Novikov Y N, Plaß W R, Rodríguez D, Scheidenberger C, Schweikhard L, Thirolf P G, Weber C 2012 Science 337 1207 Google Scholar
[14]	Hamilton J H, Hofmann S, Oganessian Y T 2013 Annu. Rev. Nucl. Part. Sci. 63 383 Google Scholar
[15]	周善贵 2014 物理 43 817 Google Scholar Zhou S G 2014 Physics 43 817 Google Scholar
[16]	周善贵 2017 原子核物理评论 34 318 Google Scholar Zhou S G 2017 Nucl. Phys. Rev. 34 318 Google Scholar
[17]	Li P C, Zhang H F, Wang Y J 2017 Chin. Phys. C 41 114103 Google Scholar
[18]	Düllmann C E, Block M 2018 Sci. Am. 318 46 Google Scholar
[19]	Nazarewicz W 2018 Nat. Phys. 14 537 Google Scholar
[20]	李竹, 牛中明, 孙保华, 王宁, 孟杰 2012 61 072601 Google Scholar Li Z, Niu Z M, Sun B H, Wang N, Meng J 2012 Acta Phys. Sin. 61 072601 Google Scholar
[21]	何建军, 周小红, 张玉虎 2013 物理 42 484 He J J, Zhou X H, Zhang Y H 2013 Physics 42 484
[22]	李竹, 孙保华, 孟杰 2013 物理 42 505 Li Z, Sun B H, Meng J 2013 Physics 42 505
[23]	Niu Z M, Niu Y F, Liang H Z, Long W H, Nikšic T, Vretenar D, Meng J 2013 Phys. Lett. B 723 172 Google Scholar
[24]	Ma C, Li Z, Niu Z M, Liang H Z 2019 Phys. Rev. C 100 024330 Google Scholar
[25]	Li Z, Miu Z M, Sun B H 2019 Sci. China, Ser. G 62 982011 Google Scholar
[26]	唐晓东, 李阔昂 2019 物理 48 633 Google Scholar Tang X D, Li K A 2019 Physics 48 633 Google Scholar
[27]	Möler P, Mumpower M R, Kawano T, Myers W D 2019 At. Data Nucl. Data Tables 125 1 Google Scholar
[28]	王猛, 张玉虎, 周小红 2020 中国科学: 物理学力学天文学 50 052006 Google Scholar Wang M, Zhang Y H, Zhou X H 2020 Sci. Sin.Phys. Mech. Astron. 50 052006 Google Scholar
[29]	Wang M, Audi G, Kondev F G, Huang W J, Naimi S, Xu X 2017 Chin. Phys. C 41 030003 Google Scholar
[30]	Möler P, Sierk A J, Ichikawa T, Sagawa H 2016 At. Data Nucl. Data Tables 109-110 1 Google Scholar
[31]	Koura H, Tachibana T, Uno M, Yamada M 2005 Prog. Theor. Phys. 113 305 Google Scholar
[32]	Wang N, Liang Z Y, Liu M, Wu X Z 2010 Phys. Rev. C 82 044304 Google Scholar
[33]	Liu M, Wang N, Deng Y G, Wu X Z 2011 Phys. Rev. C 84 014333 Google Scholar
[34]	Wang N, Liu M, Wu X Z, Meng J 2014 Phys. Lett. B 734 215 Google Scholar
[35]	Bhagwat A 2014 Phys. Rev. C 90 064306 Google Scholar
[36]	Goriely S, Chamel N, Pearson J M 2013 Phys. Rev. C 88 024308 Google Scholar
[37]	Goriely S, Chamel N, Pearson J M 2013 Phys. Rev. C 88 061302(R Google Scholar
[38]	Goriely S, Chamel N, Pearson J M 2016 Phys. Rev. C 93 034337 Google Scholar
[39]	Geng L S, Toki H, Meng J 2005 Prog. Theor. Phys. 113 785 Google Scholar
[40]	Xia X W, Lim Y, Zhao P W, Liang H Z, Qu X Y, Chen Y, Liu H, Zhang L F, Zhang S Q, Kim Y, Meng J 2018 At. Data Nucl. Data Tables 121-122 1 Google Scholar
[41]	Duflo J, Zuker A P 1995 Phys. Rev. C 52 R23(R Google Scholar
[42]	Zuker A P 2008 Rev. Mex. Fís. 54 129
[43]	Nayak R C, Satpathy L 2012 At. Data Nucl. Data Tables 98 616 Google Scholar
[44]	Sobiczewski A, Litvinov Y A 2014 Phys. Rev. C 89 024311 Google Scholar
[45]	Sobiczewski A, Litvinov Y A 2014 Phys. Rev. C 90 017302 Google Scholar
[46]	Sobiczewski A, Litvinov Y A, Palczewski M 2018 At. Data Nucl. Data Tables 119 1 Google Scholar
[47]	Zheng J S, Wang N Y, Wang Z Y, Niu Z M, Niu Y F, Sun B H 2014 Phys. Rev. C 90 014303 Google Scholar
[48]	Hua X M, Heng T H, Niu Z M, Sun B H, Guo J Y 2012 Sci. China, Ser. G 55 2414 Google Scholar
[49]	Niu Z M, Fang J Y, Niu Y F 2019 Phys. Rev. C 100 054311 Google Scholar

[1]	Jiao Bao-Bao. Nucleus density based new relationship of nuclear charge radius. Acta Physica Sinica, 2023, 72(11): 112101. doi: 10.7498/aps.72.20230126
[2]	Lou Yue-Shen, Guo Wen-Jun. Prediction of unknown nuclear stability by Bayesian deep neural network. Acta Physica Sinica, 2022, 71(10): 102101. doi: 10.7498/aps.71.20212387
[3]	Liu Zhao-Bin, Li Kai, Zeng Tian-Hai, Wang Feng, Song Xin-Bing, Shao Bin, Zou Jian. Influence of hydrogen-like nucleus mass on electronic state. Acta Physica Sinica, 2021, 70(7): 070301. doi: 10.7498/aps.70.20201754
[4]	Jin Dong-Yue, Chen Hu, Wang You, Zhang Wan-Rong, Na Wei-Cong, Guo Bin, Wu Ling, Yang Shao-Meng, Sun Sheng. Process deviation based electrical model of voltage controlled magnetic anisotropy magnetic tunnel junction and its application in read/write circuits. Acta Physica Sinica, 2020, 69(19): 198502. doi: 10.7498/aps.69.20200228
[5]	Li Jing-Tian, Wang Jian-Lu, Zhang Bang-Qiang, Rong Xi-Ming, Ning Xi-Jing. A statistical model to predict the steady-state creep rate. Acta Physica Sinica, 2014, 63(2): 028101. doi: 10.7498/aps.63.028101
[6]	Li Zhu, Niu Zhong-Ming, Sun Bao-Hua, Wang Ning, Meng Jie. WLW mass model in nuclear r-process calculations. Acta Physica Sinica, 2012, 61(7): 072601. doi: 10.7498/aps.61.072601
[7]	Feng You-Jun, Lin Zhong-Xiao, Zhang Rong-Zhu. The influence of root mean square phase gradient of continuous phase plate on smoothing focal spot. Acta Physica Sinica, 2011, 60(10): 104202. doi: 10.7498/aps.60.104202
[8]	Ling Rui-Liang, Feng Jin-Fu. Exact wave function of the coupled harmonic oscillator with time-dependent mass and frequency. Acta Physica Sinica, 2009, 58(4): 2164-2167. doi: 10.7498/aps.58.2164
[9]	Ding Bin-Gang, Zhang Da-Li, Lu Ding-Hui. Stability of traditional neutron magic numbers. Acta Physica Sinica, 2009, 58(2): 865-870. doi: 10.7498/aps.58.865
[10]	Li Yong-Qing, Li Xi-Guo, Liu Zi-Yu, Luo Pei-Yan, Zhang Peng-Ming. New vortex solutions of Jackiw-Pi model. Acta Physica Sinica, 2007, 56(11): 6178-6182. doi: 10.7498/aps.56.6178
[11]	. The disappearance of conventional magic numbers and the appearance of new numbers near drip-line region studied using relativistic mean-field plus BCS model. Acta Physica Sinica, 2007, 56(12): 6905-6910. doi: 10.7498/aps.56.6905
[12]	GUAN PENG, LIU YI-HUA. A NEW MODEL FOR INDUCED ANISOTROPY IN AMORPHOUS ALLOYS. Acta Physica Sinica, 1989, 38(7): 1182-1186. doi: 10.7498/aps.38.1182
[13]	LU MING, ZHANG QIANG-JI. A NEW MODEL FOR Ta2O5/Ta INTERFACE ANALYSIS. Acta Physica Sinica, 1989, 38(11): 1771-1777. doi: 10.7498/aps.38.1771
[14]	LAN TIAN, XU FEI-YUE. A NEW ATOMIC STRUCTURE MODEL OF Si {001} 2×1 SURFACE. Acta Physica Sinica, 1989, 38(7): 1069-1076. doi: 10.7498/aps.38.1069
[15]	XING DING-YU, YUAN JIAN. MEAN-SQUARE DISPLACEMENTS OF ATOMS IN A SEMI-INFINITE SUPERLATTICE. Acta Physica Sinica, 1986, 35(6): 812-818. doi: 10.7498/aps.35.812
[16]	QIAN KUN-MING, LIN ZHAO-HUA, DAI DAO-SHENG. NEW MODELS FOR EXCITATION OF SPIN WAVE RESONANCE. Acta Physica Sinica, 1983, 32(12): 1547-1556. doi: 10.7498/aps.32.1547
[17]	DU DONG-SHENG. A NEW POSSIBLE MODEL FOR THE STRUCTURE OF HADRONS. Acta Physica Sinica, 1976, 25(3): 265-267. doi: 10.7498/aps.25.265
[18]	LI XIAO-YUAN, DU DONG-SHENG, WU JI-MIN. A POSSIBLE MESON SPECTRUM AND THE PRODUCTION AND DECAY OF THE NEW PARTICLES IN THE SU₃⁽¹⁾×SU₃⁽²⁾ MODEL. Acta Physica Sinica, 1976, 25(6): 541-545. doi: 10.7498/aps.25.541
[19]	. . Acta Physica Sinica, 1975, 24(5): 351-365. doi: 10.7498/aps.24.351
[20]	LI CHENG-WU. MASSES OF LIGHT NUCLEI. Acta Physica Sinica, 1957, 13(1): 30-57. doi: 10.7498/aps.13.30

Catalog

Vol. 70, Issue 10 - 2021-05-20

Metrics

Abstract views: 6541
PDF Downloads: 188
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板