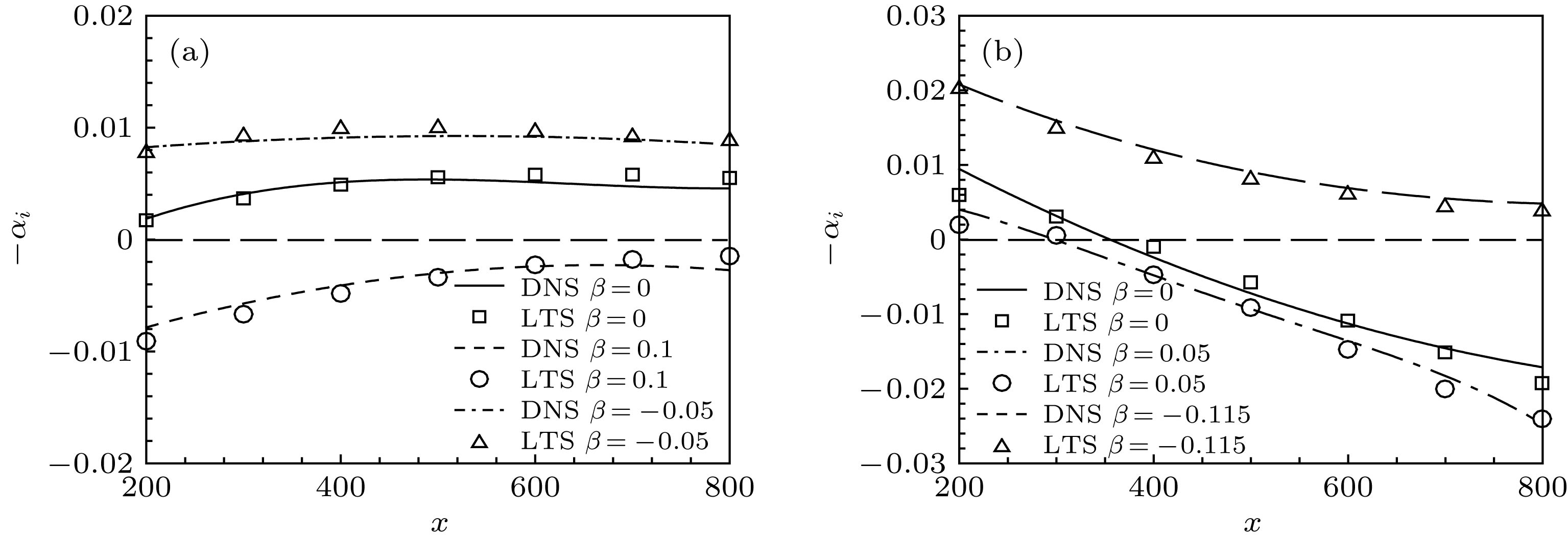
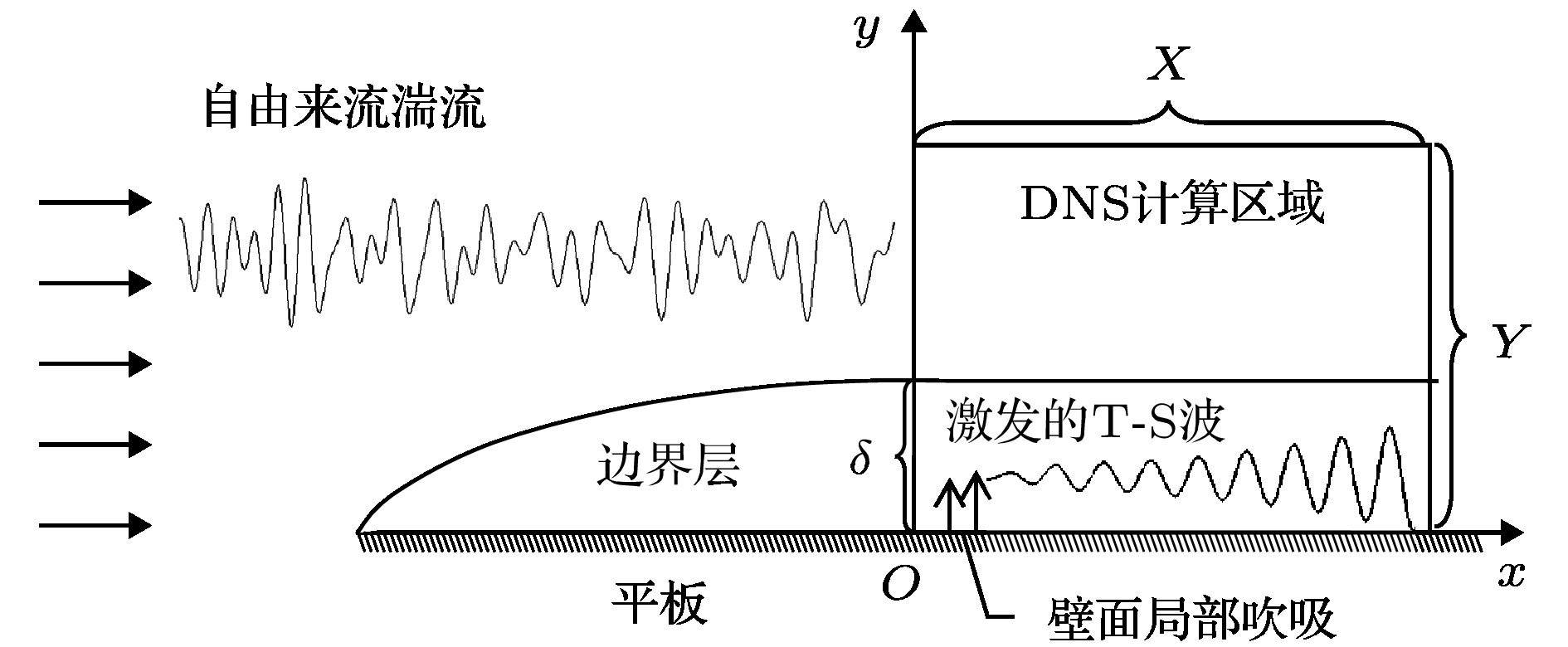
-
Boundary-layer receptivity is the initial stage of the laminar-turbulent transition process, and plays a key role in predicting and controlling the transition. The present researches indicate that the boundary-layer receptivity is affected not only by the different sorts of free-stream disturbances or the size, shape and position of the wall localized roughness and blowing/suction, but also by the pressure gradient. Therefore, the local receptivity under the interaction between the free-stream turbulence and localized wall blowing/suction in the pressure-gradient boundary layer is studied in the present work, thus revealing the effect of the pressure gradient on the receptive process and the group speeds of the excited T-S wave packets under the interaction of the free-stream turbulence with localized wall blowing/suction in the boundary layer. High-order finite difference scheme is utilized to discretize the incompressible perturbation Navier-Stokes equation. A modified fourth-order Runge-Kutta scheme is used for time integration. The compact difference scheme based on non-uniform meshes is applied to the spatial discretization. The convective term is discretized by the fifth-order upwind compact scheme. The pressure gradient term is discretized by the sixth-order symmetric compact scheme. The viscosity term is discretized by the fifth-order symmetric compact scheme. Besides, the pressure Poisson equation is solved by the fourth-order scheme on the non-uniform meshes. The favorable or adverse pressure gradient promotes or suppresses the receptivity triggered by the interaction between free-stream turbulence and blowing/suction. And the blowing always induces a stronger receptivity than the suction in the same intensity. The initial amplitude of the T-S wave and wave packet excited in the adverse-pressure-gradient boundary layer are two orders larger than those excited in the favorable-pressure-gradient boundary layer. It is analyzed in detail that the favorable and adverse pressure gradient play a promoting or suppressing role in the growth of the excited T-S wave. Then the influences of the pressure gradient on the amplitudes, growth rates, wave numbers, phase speeds and shape functions of the excited T-S waves are investigated. The intensive research on receptivity in the pressure-gradient boundary layers provides a reference for designing the turbine machinery blades in the practical engineering.
-
Keywords:
- receptivity /
- pressure gradient /
- boundary-layer
[1] Goldstein M E 1983 J. Fluid. Mech. 127 59
Google Scholar
[2] Ruban A I 1984 Fluid Dynam. 19 709
[3] 陆昌根, 沈露予 2015 65 194701
Google Scholar
Lu C G, Shen L Y 2015 Acta Phys. Sin. 65 194701
Google Scholar
[4] Shen L, Lu C, Zhu X 2019 Appl. Math. Mech. 40 851
Google Scholar
[5] Goldstein M E 1985 J. Fluid. Mech. 154 509
Google Scholar
[6] Saric W S, Hoos J A, Radeztsky R H 1991 Proceedings of the Symposium and Joint Fluids Engineering Conference, 1st Portland, U.S.A, June 23−27, 1991 p17
[7] Wiegel M, Wlezien R 1993 AIAA P. 3280
[8] Dietz A J 1999 J. Fluid. Mech. 378 291
Google Scholar
[9] Dietz A J 1998 AIAA J. 36 1171
Google Scholar
[10] Dietz A J 1996 AIAA P. 2083
[11] Wu X 2001 J. Fluid. Mech. 449 373
Google Scholar
[12] Wu X 2001 J. Fluid. Mech. 431 91
Google Scholar
[13] Shen L, Lu C 2016 Appl. Math. Mech. 37 929
Google Scholar
[14] Shen L, Lu C 2016 Appl. Math. Mech. 37 349
Google Scholar
[15] Würz W, Herr S, Wörner A, Rist U 2003 J. Fluid. Mech. 478 135
Google Scholar
[16] Shen L, Lu C 2018 Adv. Appl. Math. Mech. 10 735
Google Scholar
[17] 陆昌根, 沈露予 2015 64 224702
Google Scholar
Lu C G, Shen L Y 2015 Acta Phys. Sin. 64 224702
Google Scholar
[18] Johnson M W, Pinarbasi 2014 Flow Turbul. Combu. 93 1
Google Scholar
[19] Jacobs R G 2001 J. Fluid. Mech. 428 185
Google Scholar
-
图 1 数值计算区域示意图
Figure 1. The domain of numerical simulation.
图 2 在压力梯度(a) βH = 0.1, (b) βH = 0和(c) βH = –0.05情况下壁面局部吹入边界层内被激发出T-S波波包沿流向呈现增长的演化趋势
Figure 2. The streamwise evolutions of the excited T-S waves under the localized suction in the pressure-gradient boundary layers of (a) βH = 0.1, (b) βH = 0 and (c) βH = –0.05.
图 3 局部吹入和吸出边界层内被激发出T-S波包初始幅值AR与压力梯度的关系 (a) 吹入强度; (b) 吸出强度
Figure 3. The relationships between the initial amplitudes of the excited T-S waves AR and the pressure-gradients in the localized blowing and suction boundary layers: (a) Blowing intensity; (b) suction intensity
图 4 不同压力梯度对壁面局部吹入边界层内被激发出的T-S波沿x向发展的影响 (a) F = 40; (b) F = 80
Figure 4. The effect of different pressure gradients on x-direction evolutions of the excited T-S waves in the localized blowing boundary layers. (a) F = 40; (b) F = 80
图 5 壁面局部吹入边界层内被激发出T-S波的幅值AT-S沿x向的演化(t = 2400) (a) F = 40; (b) F = 80
Figure 5. The x-direction evolutions of the amplitude of the excited T-S waves in the local blowing boundary layers (t = 2400): (a) F = 40; (b) F = 80.
图 6 壁面局部吹入边界层内被激发出T-S波的增长率(–αi)沿x向的演化(t = 2400) (a) F = 40; (b) F = 80
Figure 6. The x-direction evolutions of the growth rate (–αi) of the excited T-S waves in the local blowing boundary layers (t = 2400): (a) F = 40; (b) F = 80.
图 7 在不同压力梯度情况下壁面局部吹入和吸出边界层内被激发出T-S波波包的初始幅值AR与局部吹吸强度q之间的关系
Figure 7. The relationships between the initial amplitudes of the excited T-S waves AR and the localized blowing/suction intensity q in different pressure boundary layers
图 8 压力梯度对壁面局部吹入边界层内被激发出T-S波的特征形状函数的幅值沿y向演变的影响(x = 300)
Figure 8. The effects of different pressure gradients on y-direction amplitude profiles of the shape functions of the excited T-S waves in localized blowing boundary layers (x = 300).
图 9 压力梯度对壁面局部吹入边界层内被激发出T-S波的特征形状函数的相位沿y向演变的影响(x = 300)
Figure 9. The effects of different pressure gradients on y-direction phase profiles of the shape functions of the excited T-S waves in localized blowing boundary layers (x = 300).
表 1 压力梯度对边界层内被激发出T-S波波包向前传播的群速度(Cg)的影响
Table 1. The group speeds (Cg) of the excited T-S wave packets in the pressure-gradient boundary layers.
βH 0.3 0.1 0.05 0 –0.05 –0.1 Cg (吹入) 0.358 0.348 0.343 0.336 0.333 0.331 Cg (吸出) 0.356 0.347 0.341 0.334 0.332 0.329 
DownLoad: CSV
表 2 压力梯度边界层被激发出的T-S波的流向波数和相速度(αr, C)
Table 2. The streamwise wave numbers and phase speeds (αr, C) of the excited T-S wave packets in the pressure-gradient boundary layers.
βH –0.1 –0.05 0 0.05 0.1 F = 30(吹) (0.0977, 0.3071) (0.0960, 0.3125) (0.0949, 0.3161) (0.0934, 0.3212) (0.0915, 0.3279) F = 30(吸) (0.0984, 0.3049) (0.0967, 0.3102) (0.0956, 0.3138) (0.0943, 0.3181) (0.0923, 0.3250) F = 40(吹) (0.1262, 0.3169) (0.1251, 0.3197) (0.1240, 0.3226) (0.1218, 0.3284) (0.1204, 0.3322) F = 40(吸) (0.1269, 0.3152) (0.1257, 0.3182) (0.1248, 0.3205) (0.1226, 0.3263) (0.1210, 0.3306) F = 50(吹) (0.1533, 0.3262) (0.1522, 0.3285) (0.1514, 0.3303) (0.1489, 0.3357) (0.1470, 0.3401) F = 50(吸) (0.1541, 0.3245) (0.1531, 0.3266) (0.1521, 0.3287) (0.1497, 0.3340) (0.1477, 0.3385) F = 60(吹) (0.1792, 0.3348) (0.1784, 0.3363) (0.1772, 0.3386) (0.1755, 0.3419) (0.1735, 0.3458) F = 60(吸) (0.1799, 0.3335) (0.1792, 0.3348) (0.1780, 0.3371) (0.1763, 0.3403) (0.1744, 0.3440) F = 70(吹) (0.2047, 0.3419) (0.2036, 0.3438) (0.2020, 0.3465) (0.2004, 0.3493) (0.1985, 0.3526) F = 70(吸) (0.2055, 0.3406) (0.2043, 0.3426) (0.2028, 0.3451) (0.2012, 0.3479) (0.1993, 0.3512) F = 80(吹) (0.2287, 0.3498) (0.2279, 0.3510) (0.2267, 0.3529) (0.2249, 0.3557) (0.2234, 0.3581) F = 80(吸) (0.2295, 0.3486) (0.2286, 0.3500) (0.2276, 0.3515) (0.2261, 0.3538) (0.2244, 0.3565)
DownLoad: CSV
-
[1] Goldstein M E 1983 J. Fluid. Mech. 127 59
Google Scholar
[2] Ruban A I 1984 Fluid Dynam. 19 709
[3] 陆昌根, 沈露予 2015 65 194701
Google Scholar
Lu C G, Shen L Y 2015 Acta Phys. Sin. 65 194701
Google Scholar
[4] Shen L, Lu C, Zhu X 2019 Appl. Math. Mech. 40 851
Google Scholar
[5] Goldstein M E 1985 J. Fluid. Mech. 154 509
Google Scholar
[6] Saric W S, Hoos J A, Radeztsky R H 1991 Proceedings of the Symposium and Joint Fluids Engineering Conference, 1st Portland, U.S.A, June 23−27, 1991 p17
[7] Wiegel M, Wlezien R 1993 AIAA P. 3280
[8] Dietz A J 1999 J. Fluid. Mech. 378 291
Google Scholar
[9] Dietz A J 1998 AIAA J. 36 1171
Google Scholar
[10] Dietz A J 1996 AIAA P. 2083
[11] Wu X 2001 J. Fluid. Mech. 449 373
Google Scholar
[12] Wu X 2001 J. Fluid. Mech. 431 91
Google Scholar
[13] Shen L, Lu C 2016 Appl. Math. Mech. 37 929
Google Scholar
[14] Shen L, Lu C 2016 Appl. Math. Mech. 37 349
Google Scholar
[15] Würz W, Herr S, Wörner A, Rist U 2003 J. Fluid. Mech. 478 135
Google Scholar
[16] Shen L, Lu C 2018 Adv. Appl. Math. Mech. 10 735
Google Scholar
[17] 陆昌根, 沈露予 2015 64 224702
Google Scholar
Lu C G, Shen L Y 2015 Acta Phys. Sin. 64 224702
Google Scholar
[18] Johnson M W, Pinarbasi 2014 Flow Turbul. Combu. 93 1
Google Scholar
[19] Jacobs R G 2001 J. Fluid. Mech. 428 185
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 7729
- PDF Downloads: 73
- Cited By: 0
