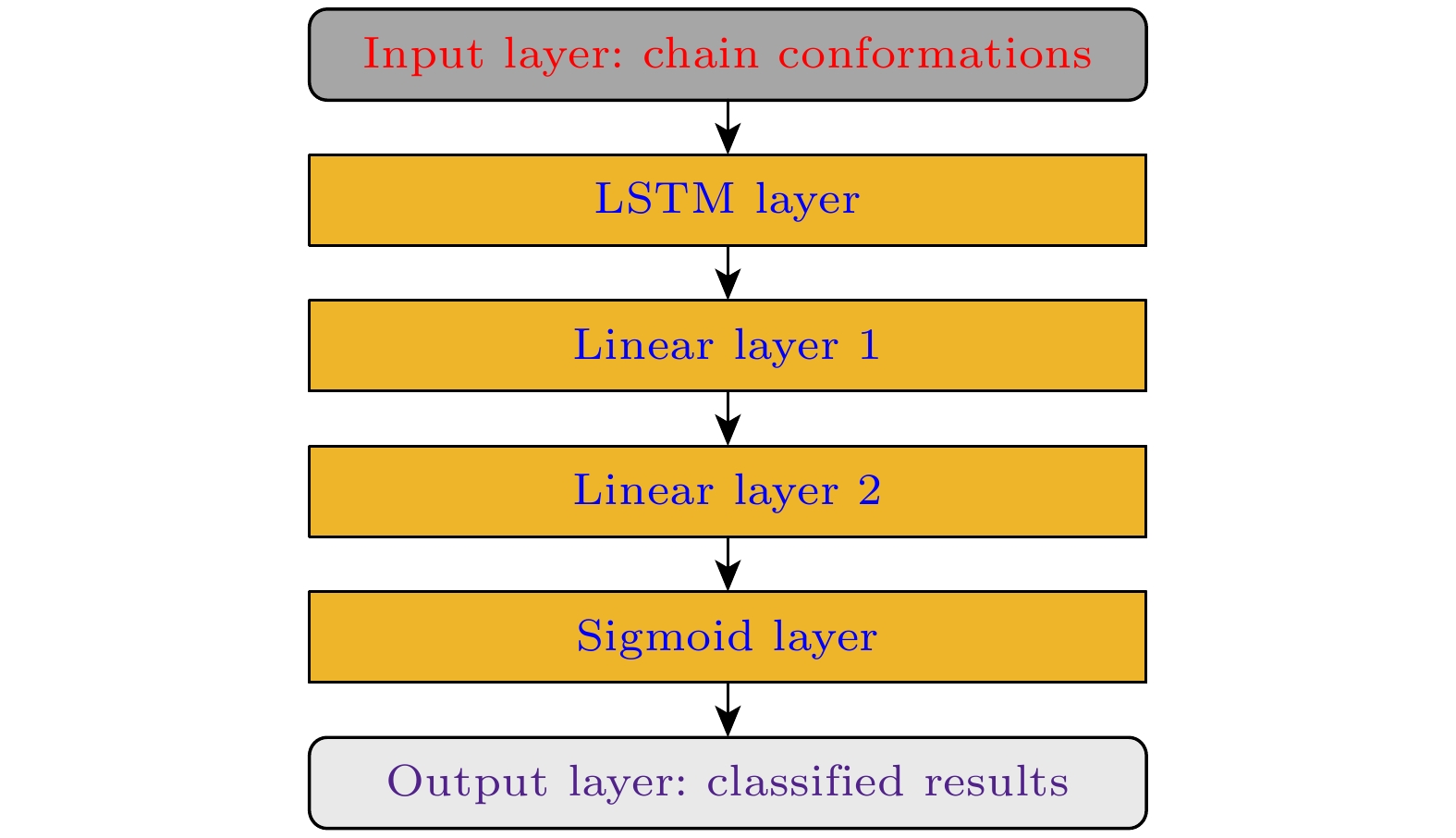
-
Collapse and critical adsorption of polymers are two crucial phase transitions in polymer science, both are accompanied by significant changes in polymer conformation. In this paper, Langevin dynamics and dynamic Monte Carlo methods are used to simulate the collapse and critical adsorption of polymer, respectively, and corresponding phase transition temperatures are estimated. Meanwhile, a large number of polymer conformations at different temperatures are obtained. In the machine learning method, a large number of extended random coil and collapsed spherical, desorption and adsorption conformations are used to train the neural network, so that the neural network can learn the characteristics of different states of the polymer, and it can quickly and accurately analyze the polymer conformations at different temperatures and obtain the corresponding collapse phase transition temperature and critical adsorption temperature. The results demonstrate that machine learning can correctly calculate the phase transition temperature of polymer system, which provides new ideas and methods for machine learning technology in the study of polymer phase transitions.
-
Keywords:
- polymer /
- collapse /
- critical adsorption /
- machine learning
[1] Hinton G, Deng L, Yu D, et al. 2012 IEEE Signal Process. Mag. 29 82
Google Scholar
[2] Silver D, Huang A, Maddison C J, et al. 2016 Nature 529 484
Google Scholar
[3] Umehara M, Stein H S, Guevarra D, et al. 2019 NPJ Comput. Mater. 5 34
Google Scholar
[4] Iwasaki Y, Takeuchi I, Stanev V, et al. 2019 Sci. Rep. 9 2751
Google Scholar
[5] 陈江芷, 杨晨温, 任捷 2021 70 144204
Google Scholar
Chen J Z, Yang C W, Ren J 2021 Acta Phys. Sin. 70 144204
Google Scholar
[6] Cencer M M, Moore J S, Assary R S 2022 Polym. Int. 71 537
Google Scholar
[7] Zhang Y, Xu X 2021 J. Mol. Graphics Modell. 103 107796
Google Scholar
[8] Liang Z, Li Z, Zhou S, et al. 2022 Cell Reports Physical Science 3 100931
Google Scholar
[9] Zhang K, Li X, Jin Y, Jiang Y 2022 Soft Matter 18 6270
Google Scholar
[10] Xu Y, Wang Z G 2021 Macromolecules 54 10984
Google Scholar
[11] Milner S T 1991 Science 251 905
Google Scholar
[12] Besteman K, Lee J O, Wiertz F G M, Heering H A, Dekker C 2003 Nano Lett. 3 727
Google Scholar
[13] Duan X, Zhang R, Ding M, Huang Q, Xu W S, Shi T, An L 2017 Polymer 122 125
Google Scholar
[14] Sumithra K, Brandau M, Straube E 2009 J. Chem. Phys. 130 234901
Google Scholar
[15] Li Y W, Wüst T, Landau D P 2013 Phys. Rev. E 87 012706
Google Scholar
[16] Yang Q H, Wu F, Wang Q, Luo M B 2016 J. Polym. Sci. Part B: Polym. Phys. 54 2359
Google Scholar
[17] Ziebarth J D, Gardiner A A, Wang Y M, Jeong Y, Ahn J, Jin Y, Chang T 2016 Macromolecules 49 8780
Google Scholar
[18] Bhattacharya D, Patra T K 2021 Macromolecules 54 3065
Google Scholar
[19] Nguyen T, Bavarian M 2022 Ind. Eng. Chem. Res. 61 12690
Google Scholar
[20] Weeks J D, Chandler D, Andersen H C 1971 J. Chem. Phys. 54 5237
Google Scholar
[21] Chremos A, Glynos E, Koutsos V, Camp P J 2009 Soft Matter 5 637
Google Scholar
[22] Hochreiter S, Schmidhuber J A 1997 Neural Comput. 9 1735
Google Scholar
[23] Loshchilov I, Hutter F 2017 arXiv:1711.05101 [cs.LG
[24] Luo M B, Tsehay D A, Sun L Z 2017 J. Chem. Phys. 147 034901
Google Scholar
[25] Yang X, Wu F, Hu D D, Zhang S, Luo M B 2019 Chin. Phys. Lett. 36 098202
Google Scholar
[26] Qi H K, Yang X, Yang Q H, Luo M B 2022 Polymer 259 125330
Google Scholar
-
图 1 模拟高分子的示意图 (a) 稀溶液中的高分子; (b) 低接枝密度的孤立接枝高分子
Figure 1. Schematic diagram of simulated polymers: (a) A polymer in dilute solution; (b) an isolated grafted polymer at low grafting density.
图 2 机器学习的流程图
Figure 2. Flowchart of machine learning.
图 3 机器学习中的损失随训练次数的变化
Figure 3. Loss in machine learning varies with the number of trainings.
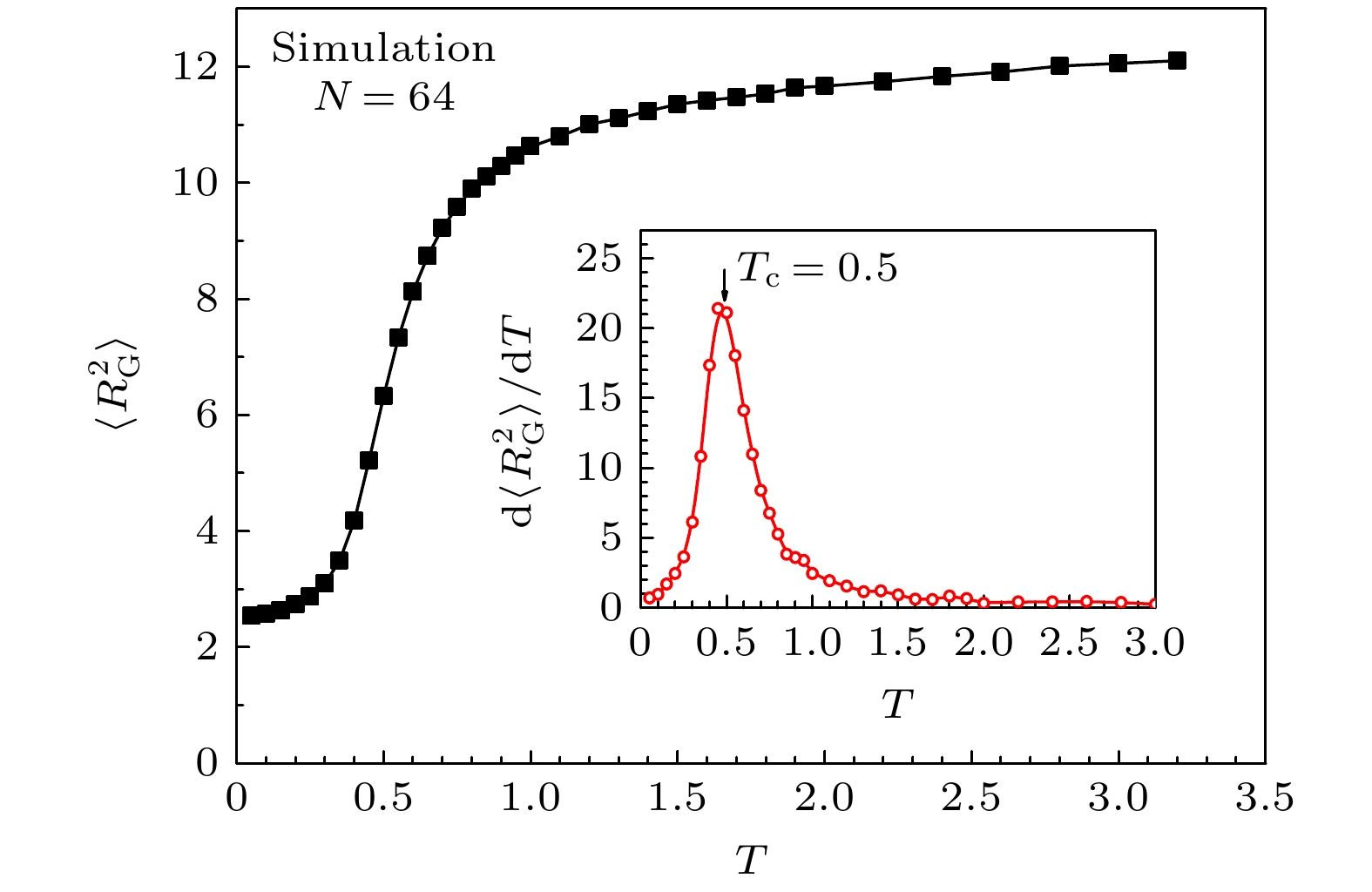
图 4 高分子均方回转半径$ \left\langle{{R}_{{\mathrm{G}}}^{2}}\right\rangle $与温度T的关系的朗之万动力学模拟结果. 插图给出了$ \left\langle{{R}_{{\mathrm{G}}}^{2}}\right\rangle $对T的导数与T的关系
Figure 4. Simulation results of the mean square radius of gyration $ \left\langle{{R}_{{\mathrm{G}}}^{2}}\right\rangle $ versus temperature T. The inset presents the $ \left\langle{{R}_{{\mathrm{G}}}^{2}}\right\rangle $ derivative of T in relation to T.
图 5 高分子平方回转半径$ {R}_{{\mathrm{G}}}^{2} $在温度T = 0.01 (a), 0.5 (b)和3.2 (c)的概率分布. 插图分别给出了T = 0.01 和 3.2 时高分子的典型构象
Figure 5. Plots of the probability distribution of square radius of gyration $ {R}_{{\mathrm{G}}}^{2} $ for polymer at temperatures T = 0.01 (a), 0.5 (b), and 3.2 (c). The insets show the typical polymer conformations at T = 0.01 and 3.2.
图 6 高分子处于塌缩态的平均概率PG与温度T关系的机器学习结果. 插图给出了|dPG/dT| 随T的变化.
Figure 6. Machine learning results of the mean probability of polymer being in the compact globule state, PG, versus temperature T. The inset shows the change of |dPG/dT| with temperature T.
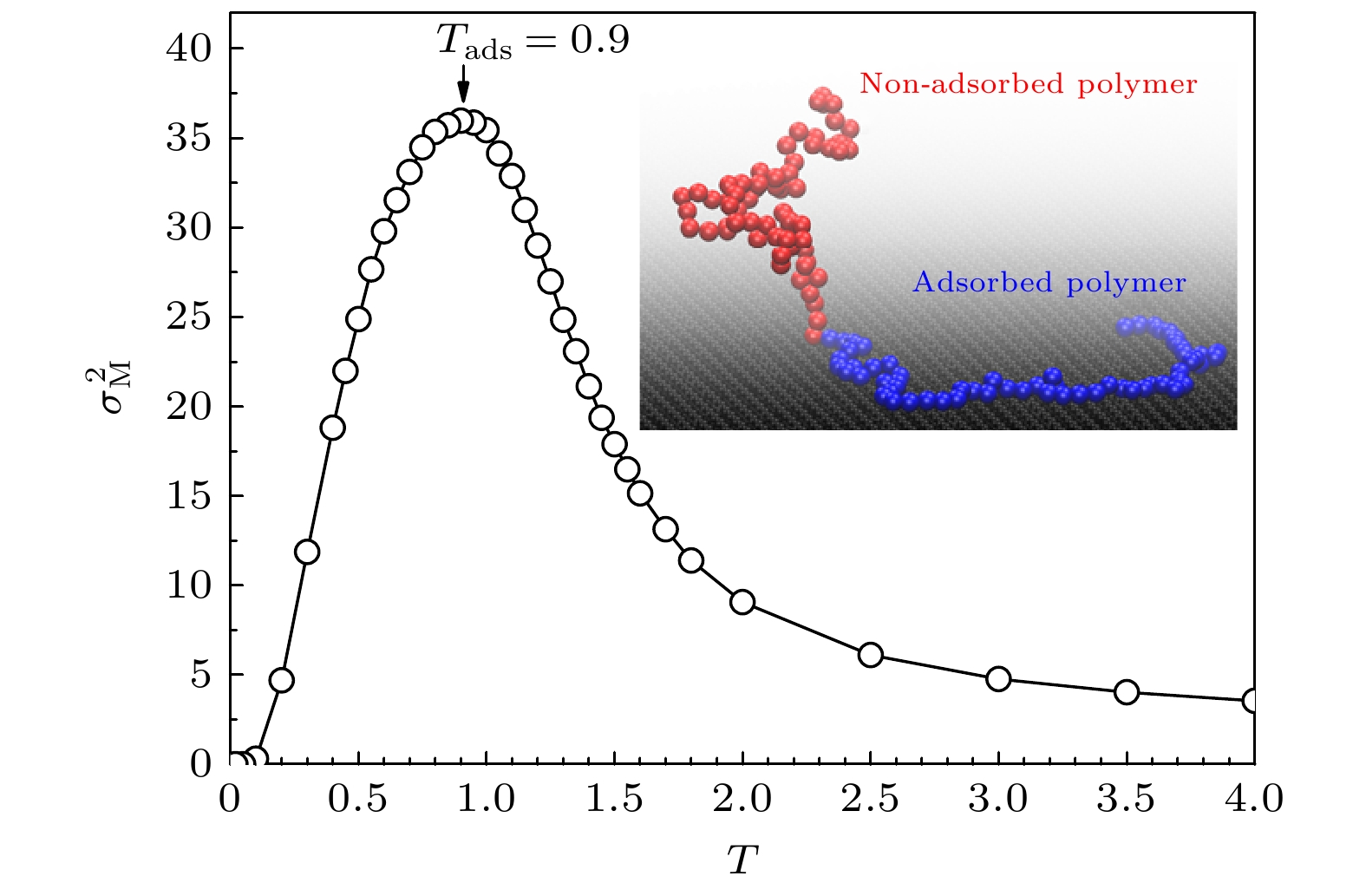
图 7 高分子吸附链节数涨落$ {\sigma }_{\rm M}^{2} $与温度T的关系的动力学Monte Carlo模拟结果. 插图给出了高温的非吸附态和低温的吸附态高分子构象
Figure 7. Plot of the fluctuation of adsorption monomer number $ {\sigma }_{\rm M}^{2} $ of polymer chain versus temperature T. The inset presents non-adsorbed polymer at high temperature and adsorbed polymer at low temperature.
图 8 高分子处于吸附态的平均概率PA和温度变化率|dPA/dT|与温度T的关系的机器学习结果
Figure 8. Plot of the mean adsorption probability PA of polymer and its temperature change rate dPA/dT versus temperature T.
图 9 利用高分子构象的三维坐标和z坐标进行机器学习得到的高分子处于吸附态的概率PA与温度T的关系
Figure 9. Relationship between adsorption probability PA and temperature T obtained by machine learning using the three-dimensional coordinates and z-coordinates only of polymer conformations.
图 10 机器学习得到的吸附态概率PA在(0, 0.2), (0.2, 0.8)和(0.8, 1)三个范围内高分子构象相对于构象的吸附数M和链质心高度zc的分布
Figure 10. Distribution of polymer conformation relative to the adsorbed number M and the mean height zc for the adsorption probability PA obtained by machine learning in three ranges of (0, 0.2), (0.2, 0.8) and (0.8, 1).
-
[1] Hinton G, Deng L, Yu D, et al. 2012 IEEE Signal Process. Mag. 29 82
Google Scholar
[2] Silver D, Huang A, Maddison C J, et al. 2016 Nature 529 484
Google Scholar
[3] Umehara M, Stein H S, Guevarra D, et al. 2019 NPJ Comput. Mater. 5 34
Google Scholar
[4] Iwasaki Y, Takeuchi I, Stanev V, et al. 2019 Sci. Rep. 9 2751
Google Scholar
[5] 陈江芷, 杨晨温, 任捷 2021 70 144204
Google Scholar
Chen J Z, Yang C W, Ren J 2021 Acta Phys. Sin. 70 144204
Google Scholar
[6] Cencer M M, Moore J S, Assary R S 2022 Polym. Int. 71 537
Google Scholar
[7] Zhang Y, Xu X 2021 J. Mol. Graphics Modell. 103 107796
Google Scholar
[8] Liang Z, Li Z, Zhou S, et al. 2022 Cell Reports Physical Science 3 100931
Google Scholar
[9] Zhang K, Li X, Jin Y, Jiang Y 2022 Soft Matter 18 6270
Google Scholar
[10] Xu Y, Wang Z G 2021 Macromolecules 54 10984
Google Scholar
[11] Milner S T 1991 Science 251 905
Google Scholar
[12] Besteman K, Lee J O, Wiertz F G M, Heering H A, Dekker C 2003 Nano Lett. 3 727
Google Scholar
[13] Duan X, Zhang R, Ding M, Huang Q, Xu W S, Shi T, An L 2017 Polymer 122 125
Google Scholar
[14] Sumithra K, Brandau M, Straube E 2009 J. Chem. Phys. 130 234901
Google Scholar
[15] Li Y W, Wüst T, Landau D P 2013 Phys. Rev. E 87 012706
Google Scholar
[16] Yang Q H, Wu F, Wang Q, Luo M B 2016 J. Polym. Sci. Part B: Polym. Phys. 54 2359
Google Scholar
[17] Ziebarth J D, Gardiner A A, Wang Y M, Jeong Y, Ahn J, Jin Y, Chang T 2016 Macromolecules 49 8780
Google Scholar
[18] Bhattacharya D, Patra T K 2021 Macromolecules 54 3065
Google Scholar
[19] Nguyen T, Bavarian M 2022 Ind. Eng. Chem. Res. 61 12690
Google Scholar
[20] Weeks J D, Chandler D, Andersen H C 1971 J. Chem. Phys. 54 5237
Google Scholar
[21] Chremos A, Glynos E, Koutsos V, Camp P J 2009 Soft Matter 5 637
Google Scholar
[22] Hochreiter S, Schmidhuber J A 1997 Neural Comput. 9 1735
Google Scholar
[23] Loshchilov I, Hutter F 2017 arXiv:1711.05101 [cs.LG
[24] Luo M B, Tsehay D A, Sun L Z 2017 J. Chem. Phys. 147 034901
Google Scholar
[25] Yang X, Wu F, Hu D D, Zhang S, Luo M B 2019 Chin. Phys. Lett. 36 098202
Google Scholar
[26] Qi H K, Yang X, Yang Q H, Luo M B 2022 Polymer 259 125330
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 2325
- PDF Downloads: 109
- Cited By: 0
