-
The interaction between the shock and the internal density perturbation of the target material produces a Richtmyer-Meshkov-like (RM-like) instability, which couples with the ablation front and generates instability seeds. Recent studies have demonstrated the significance of internal material density perturbations to implosion performance. This paper presents a two-dimensional numerical investigation of the growth of the RM-like instability in linear region and its coupling mechanism with the interface. Euler equations in two dimensions are solved in Cartesian coordinates by using the fifth-order WENO scheme in space and the two-step Runge-Kutta scheme in time. The computational domain has a length of 200 μm in the x-direction and λy in the y-direction. The numerical resolution adopted in this paper is
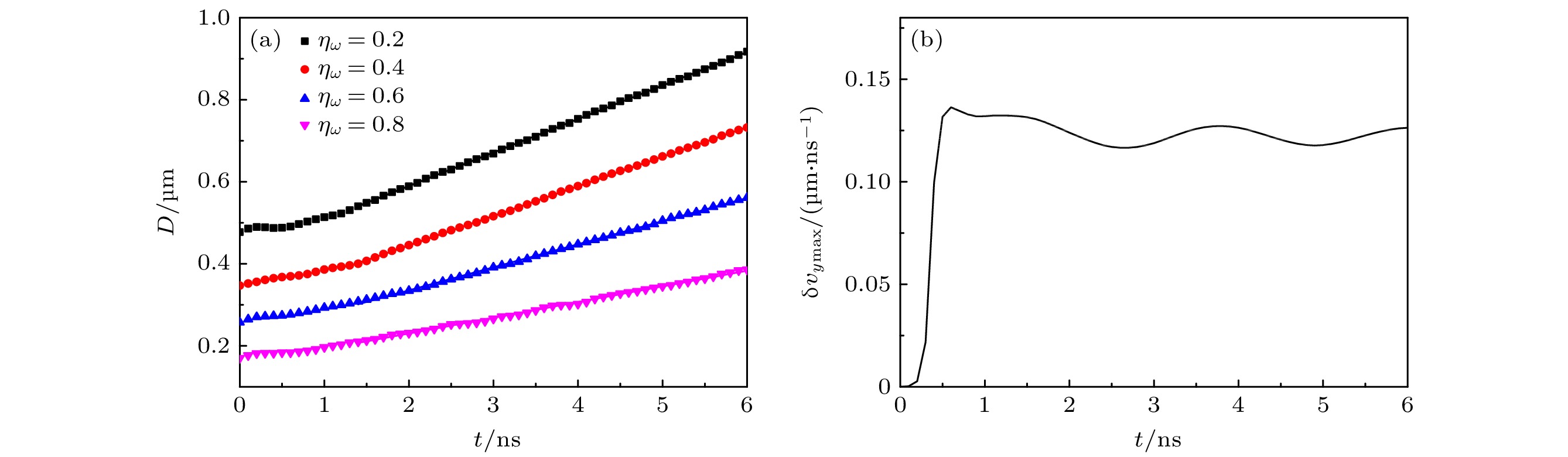
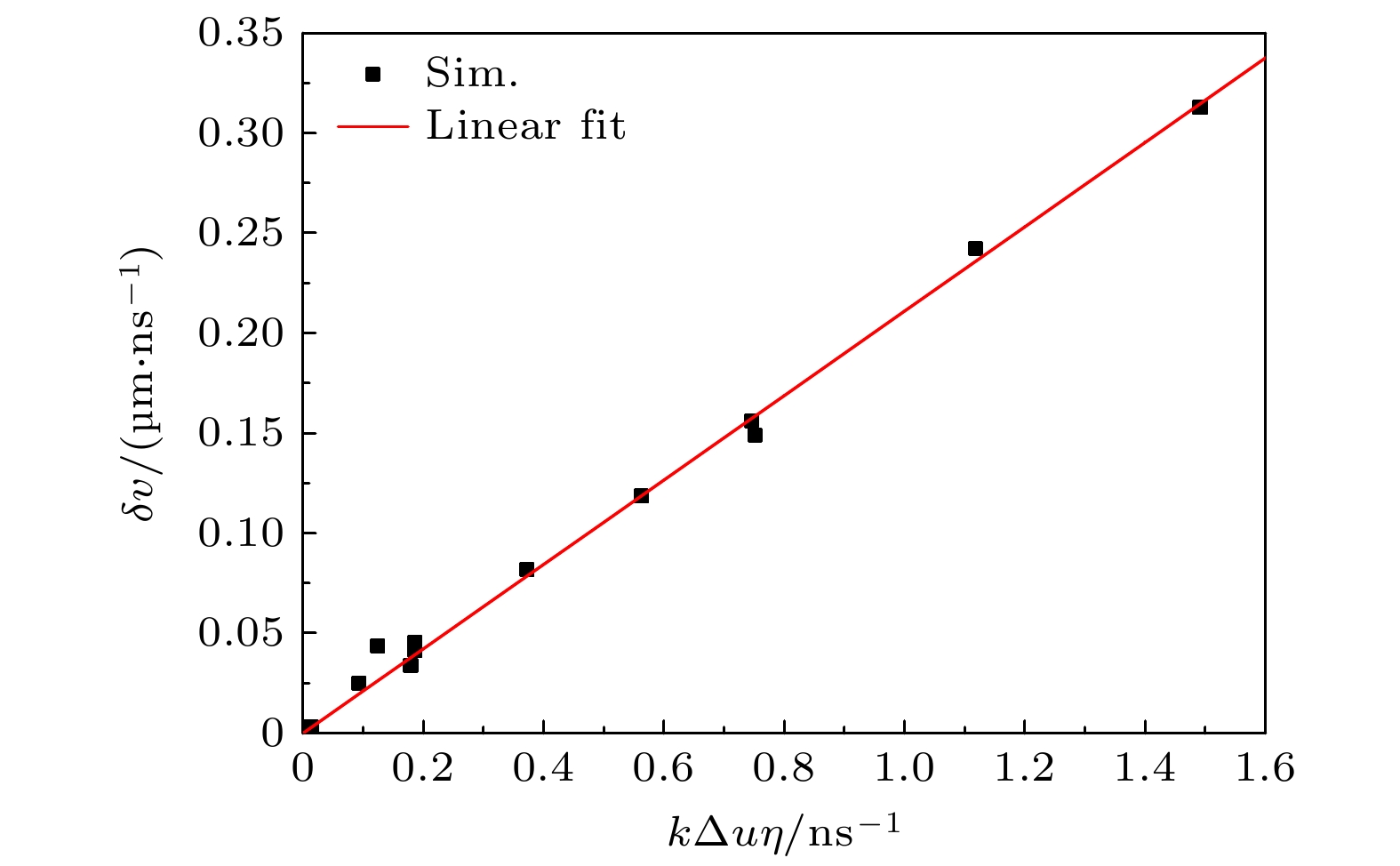
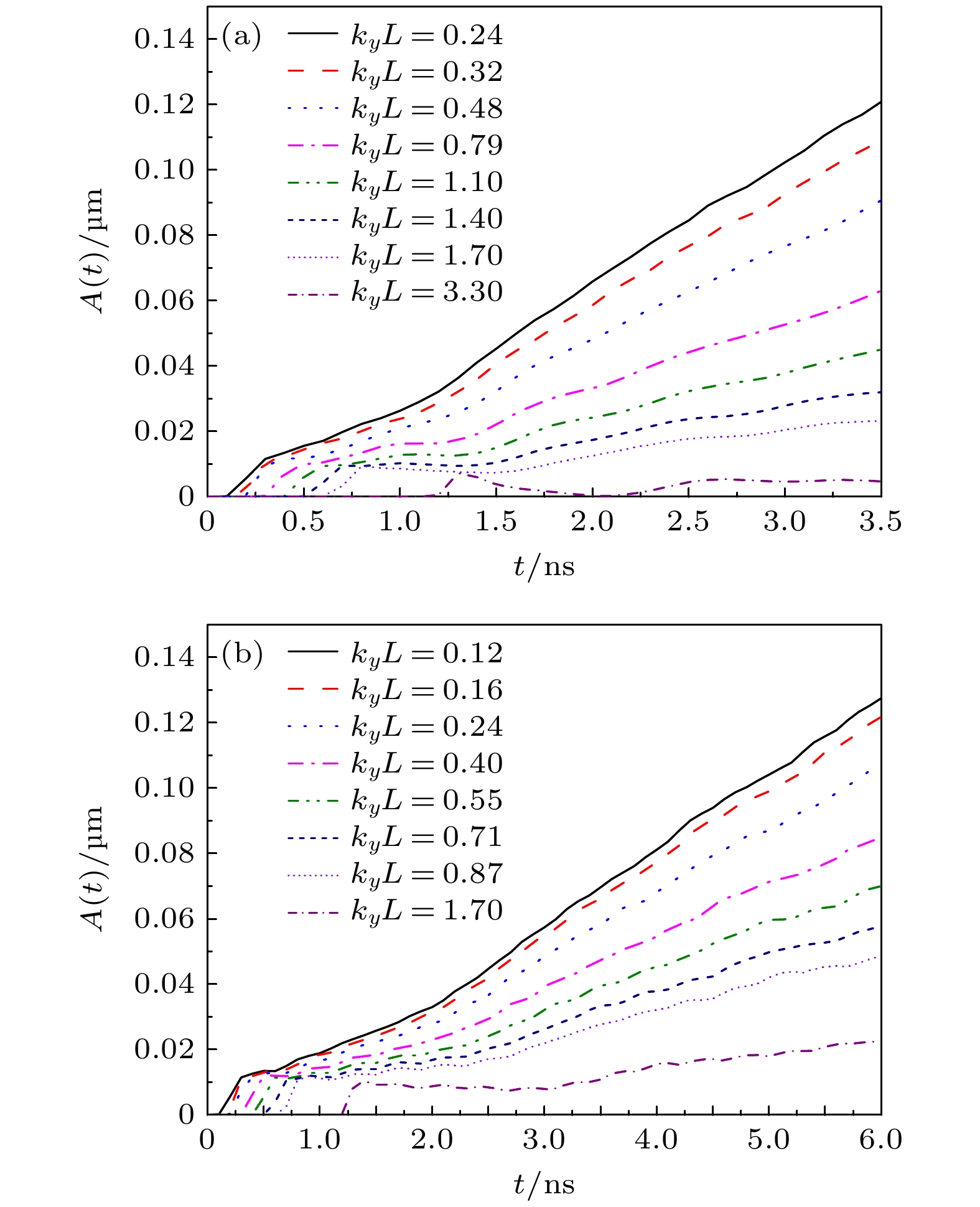
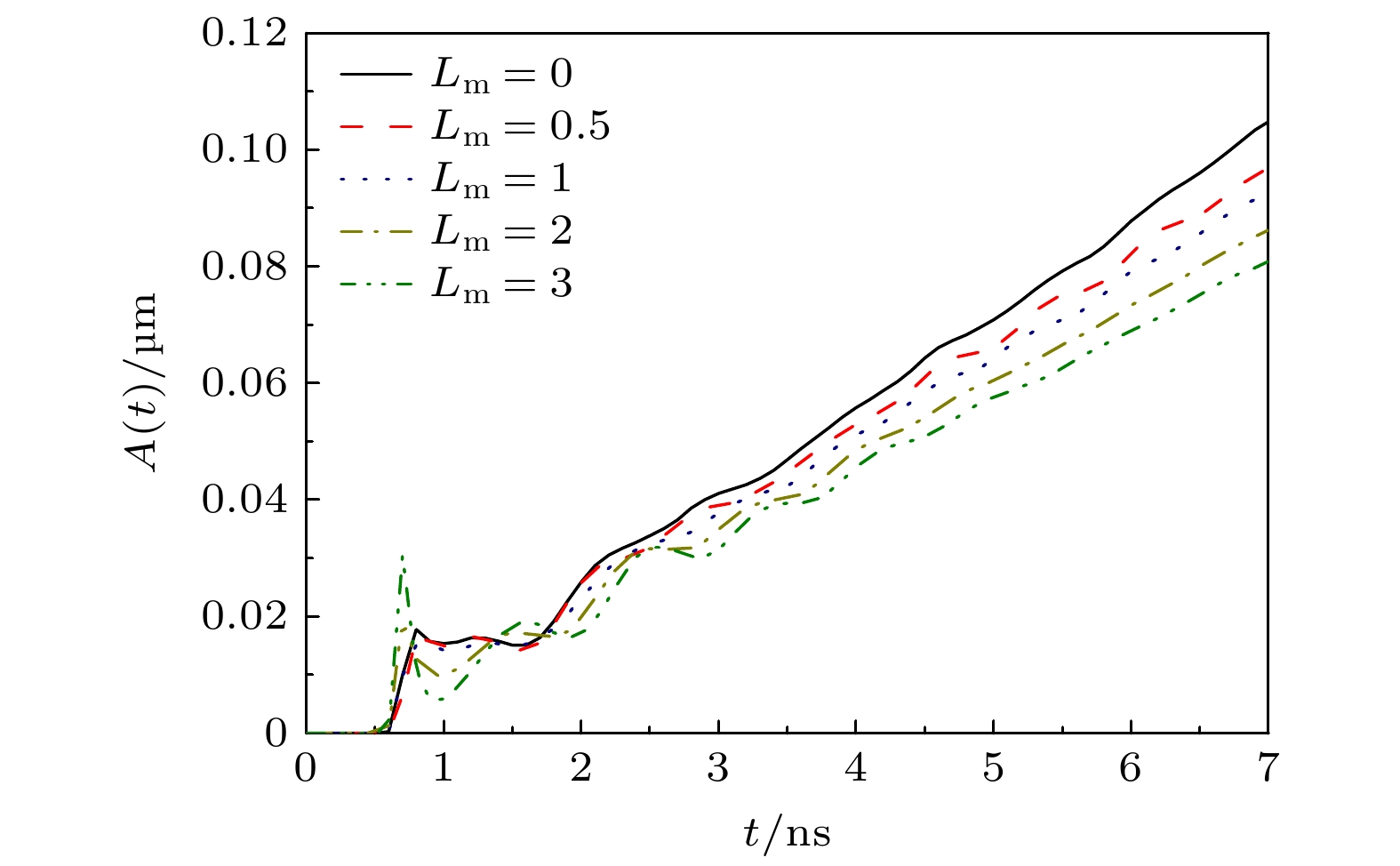
$ {\Delta _x} = {\Delta _y} = {\lambda _y}/128 $ . A periodic boundary condition is used in the y-direction, while an outflow boundary condition is used in the x-direction. The interaction between shock and density perturbation will deposit vorticity in the density perturbation region. The width of the density perturbation region can be represented by the width of the vortex pair. The growth rate of the RM-like instability can be represented by the growth rate of the width of the density-disturbed region or the maximum perturbation velocity in the y-direction. The simulation results show that the growth rate of the vortex pair width is proportional to the perturbation wave number ky, the perturbation amplitude η, and the velocity difference before and after the shock wave Δu, specifically, δv∝kyΔuη. In the problem of coupling the RM-like instability with the interface, we calculate the derivation of the interface perturbation amplitude with respect to time to obtain the growth rate of the interface. It is concluded from the simulations that the coupling of the RM-like instability with the interface has two mechanisms: acoustic coupling and vortex merging. When the density perturbation region is far from the interface, only acoustic wave is coupled with the interface. The dimensionless growth rate of interface perturbation caused by acoustic coupling decays exponentially with kyL, δvi/(kyΔuη)∝$ {{\text{e}}^{ - {k_y}L}} $ . When the density perturbation region is closer to the interface, acoustic coupling and vortex merging work together. The vortex merging leads to an increase in the perturbation velocity when the Atwood number of the interface is positive. When the Atwood number is positive, reducing the Atwood number at the interface and increasing the width of the transition layer at the interface can both reduce the growth of interface perturbation caused by the RM-like instability coupling.-
Keywords:
- inertial confinement fusion /
- density perturbation /
- Richmyer-Meshkov-like instability /
- instability seeds
[1] Craxton R S, Anderson K S, Roehly T R, Goncharov V N, Harding D R, Knauer J P, McCrory R L, McKenty M C, Meyerhofer D D, Myatt J F, Schmitt A J, Sethian J D, Short R W, Skupsky S, Theobald W, Kruer W L, Tanaka K, Betti R, Collins T J B, Delettrez J A, Hu S X, Marozas J A, Maximov A V, Michel D T, Radha P B, Regan S P, Sangster T C, Seka W, Solodov A A, Soures J M, Stoeckl C, Zuegel J D 2015 Phys. Plasmas 22 110501
Google Scholar
[2] Goncharov V N, Regan S P, Campbell E M, Sangster T C, Radha P B, Myatt J F, Froula D H, Betti R, Boehly T R, Delettrez J A, Edgell D H, Epstein R, Forrest C J, Yu Glebov V, Harding D R, Hu S X, Igumenshchev I V, Marshall F J, McCrory R L, Michel D T, Seka W, Shvydky A, Stoeckl C, Theobald W, Gatu-Johnson M 2017 Plasma Phys. Control. Fusion 59 014008
Google Scholar
[3] Campbell E M, Sangster T C, Goncharov V N, Zuegel J D, Morse S F B, Sorce C, Collins G W, Wei M S, Betti R, Regan S P, et al. 2021 Phil. Trans. R. Soc. A 379 20200011
Google Scholar
[4] Lindl J D, Amendt P, Berger R L, Glendinning S G, Glenzer S H, Haan S W, Kauffman R L, Landen O L, Suter L J 2004 Phys. Plasmas 11 339
Google Scholar
[5] Atzeni S, Meyer-ter-Vehn J 2004 The Physics of Inertial Fusion: Beam Plasma Interaction, Hydrodynamics, Hot Dense Matter (Oxford: Oxford University Press) pp198–252
[6] Zhou C D, Betti R 2007 Phys. Plasmas 14 072703
Google Scholar
[7] Rayleigh L 1883 Proc. London Math. Soc. s1 170
Google Scholar
[8] Taylor G 1950 Proc. R. Soc. London: Ser. A 201 192
Google Scholar
[9] Lindl J D, Mead W C 1975 Phys. Rev. Lett. 34 1273
Google Scholar
[10] Takabe H, Mima K, Montierth L, Morse R L 1985 Phys. Fluids 28 3676
Google Scholar
[11] Igumenshchev I V, Velikovich A L, Goncharov V N, Betti R, Campbell E M, Knauer J P, Regan S P, Schmitt A J, Shah R C, Shvydky A 2019 Phys. Rev. Lett. 123 065001
Google Scholar
[12] Peterson J L, Clark D S, Masse L P, Suter L J 2014 Phys. Plasmas 21 092710
Google Scholar
[13] Miller S C, Goncharov V N 2022 Phys. Plasmas 29 082701
Google Scholar
[14] Harding D R, Shmayda W T 2013 Fusion Sci. Technol. 63 125
Google Scholar
[15] Richtmyer R D 1960 Commun. Pure Appl. Math. 13 297
Google Scholar
[16] Meshkov E E 1969 Fluid Dyn. 4 101
Google Scholar
[17] Wouchuk J G, Nishihara K 1997 Phys. Plasmas 4 1028
Google Scholar
[18] Wouchuk J G 2001 Phys. Rev. E 63 056303
Google Scholar
[19] Wouchuk J G 2001 Phys. Plasmas 8 2890
Google Scholar
[20] Campos F C, Wouchuk J G 2016 Phys. Rev. E 93 053111
Google Scholar
[21] Campos F C, Wouchuk J G 2017 Phys. Rev. E 96 013102
Google Scholar
[22] Pickworth L A, Hammel B A, Smalyuk V A, Robey H F, Benedetti L R, Berzak Hopkins L, Bradley D K, Field J E, Haan S W, Hatarik R, Hartouni E, Izumi N, Johnson S, Khan S, Lahmann B, Landen O L, Le Pape S, MacPhee A G, Meezan N B, Milovich J, Nagel S R, Nikroo A, Pak A E, Petrasso R, Remington B A, Rice N G, Springer P T, Stadermann M, Widmann K, Hsing W 2018 Phys. Plasmas 25 054502
Google Scholar
[23] Collins T J B, Stoeckl C, Epstein R, Bittle W A, Forrest C J, Glebov V Y, Goncharov V N, Harding D R, Hu S X, Jacobs-Perkins D W, Kosc T Z, Marozas J A, Mileham C, Marshall F J 2022 Phys. Plasmas 29 012703
Google Scholar
[24] Haines B M, Olson R E, Sweet W, Yi S A, Zylstra A B, Bradley P A, Elsner F, Huang H, Jimenez R, Kline J L, Kong C, Kyrala G A, Leeper R J, Paguio R, Pajoom S, Peterson R R, Ratledge M, Rice N 2019 Phys. Plasmas 26 012707
Google Scholar
[25] Haines B M, Sauppe J P, Albright B J, Daughton W S, Finnegan S M, Kline J L, Smidt J M 2022 Phys. Plasmas 29 042704
Google Scholar
[26] Liu Y X, Chen Z, Wang L F, Li Z Y, Wu J F, Ye W H, Li Y J 2023 Phys. Plasmas 30 042704
Google Scholar
[27] Li Z Y, Wang L F, Wu J F, Ye W H 2020 Acta Mech. Sin. 36 789
Google Scholar
[28] Sano T, Ishigure K, Campos F C 2020 Phys. Rev. E 102 013203
Google Scholar
[29] Goncharov V N 1999 Phys. Rev. Lett. 82 2091
Google Scholar
[30] Goncharov V N, Gotchev O V, Vianello E, Boehly T R, Knauer J P, McKenty P W, Radha P B, Regan S P, Sangster T C, Skupsky S, Smalyuk V A, Betti R, McCrory R L, Meyerhofer D D, Cherfils-Clérouin C 2006 Phys. Plasmas 13 012702
Google Scholar
[31] Mikaelian K O 1985 Phys. Rev. A 31 410
Google Scholar
[32] Mikaelian K O 1983 Phys. Rev. A 28 1637
Google Scholar
-
图 1 数值模拟初始设置示意图
Figure 1. Schematics of the initial configuration.
图 2 算例SPI1在1 ns (a)和3 ns (b)时的涡量场. 蓝色圈起部分为密度扰动区域, 红色虚线标注了冲击波位置
Figure 2. Contour of vorticity at 1 ns (a) and 3 ns (b) of case SPI1. Blue circled part is the density perturbation region, and the red dashed line indicates the position of the shock.
图 3 算例SPI1的涡对宽度(a)和y方向最大扰动速度(b)随时间的变化
Figure 3. Time histories of the width of the vortex pair (a) and the maximum tangential velocity (b) of case SPI1.
图 4 密度扰动宽度增长速度δv随kyΔuη的变化
Figure 4. Curve of density perturbation width growth rate δv versus kyΔuη.
图 5 类RM不稳定性与界面耦合问题的密度云图, 此算例中的物理参数为Ma = 9.5, η = 0.3, λy = 20 μm, At = 0.77
Figure 5. Contour of density of the RM-like instability and interface coupling problem, the physical parameters in this case are Ma = 9.5, η = 0.3, λy = 20 μm, At = 0.77.
图 6 y方向扰动速度云图 (a) L = 5.53 μm; (b) L = 3.53 μm; (c) L = 1.53 μm. 物理参数Ma = 9.5, η = 0.05, λy = 20 μm, At = 0.77
Figure 6. Contour of the y-component of the perturbation velocity: (a) L = 5.53 μm; (b) L = 3.53 μm; (c) L = 1.53 μm. Physical parameters: Ma = 9.5, η = 0.05, λy = 20 μm, At = 0.77.
图 7 不同L时, 界面扰动幅值随时间的变化 (a) λy = 20 μm; (b) λy = 40 μm.
Figure 7. Variation of interface perturbation amplitudes with time for different L: (a) λy = 20 μm; (b) λy = 40 μm.
图 8 界面扰动增长速度δvi/(kyΔuη)随
$ {{\text{e}}^{ - {k_y}L}} $ 的变化Figure 8. Curve of the interface disturbance growth rate δvi/(kyΔuη) versus
$ {{\text{e}}^{ - {k_y}L}} $ .
图 9 不同界面Atwood数时, 界面扰动幅值随时间的变化
Figure 9. Time evolution of interface perturbation amplitude at different Atwood numbers.
图 10 不同界面过渡层宽度时, 界面扰动幅值随时间的变化
Figure 10. Time evolution of interface perturbation amplitude with different density transition layer
表 1 不同算例的参数设置
Table 1. Initial physical parameters in different cases.
算例 SPI1 SPI2 SPI3 SPI4 SPI5 SPI6 SPI7 SPI8 SPI9 SPI10 SPI11 SPI12 η 0.1 0.1 0.1 0.1 0.05 0.2 0.3 0.4 0.1 0.1 0.1 0.1 Ma M0 M0 M0 M0 M0 M0 M0 M0 M0/8 M0/2 1.5M0 2.0M0 λy/μm 20 40 60 80 20 20 20 20 20 20 20 20 kyΔuη 0.037 0.019 0.012 0.009 0.019 0.075 0.11 0.15 0.0014 0.018 0.056 0.075 
DownLoad: CSV
-
[1] Craxton R S, Anderson K S, Roehly T R, Goncharov V N, Harding D R, Knauer J P, McCrory R L, McKenty M C, Meyerhofer D D, Myatt J F, Schmitt A J, Sethian J D, Short R W, Skupsky S, Theobald W, Kruer W L, Tanaka K, Betti R, Collins T J B, Delettrez J A, Hu S X, Marozas J A, Maximov A V, Michel D T, Radha P B, Regan S P, Sangster T C, Seka W, Solodov A A, Soures J M, Stoeckl C, Zuegel J D 2015 Phys. Plasmas 22 110501
Google Scholar
[2] Goncharov V N, Regan S P, Campbell E M, Sangster T C, Radha P B, Myatt J F, Froula D H, Betti R, Boehly T R, Delettrez J A, Edgell D H, Epstein R, Forrest C J, Yu Glebov V, Harding D R, Hu S X, Igumenshchev I V, Marshall F J, McCrory R L, Michel D T, Seka W, Shvydky A, Stoeckl C, Theobald W, Gatu-Johnson M 2017 Plasma Phys. Control. Fusion 59 014008
Google Scholar
[3] Campbell E M, Sangster T C, Goncharov V N, Zuegel J D, Morse S F B, Sorce C, Collins G W, Wei M S, Betti R, Regan S P, et al. 2021 Phil. Trans. R. Soc. A 379 20200011
Google Scholar
[4] Lindl J D, Amendt P, Berger R L, Glendinning S G, Glenzer S H, Haan S W, Kauffman R L, Landen O L, Suter L J 2004 Phys. Plasmas 11 339
Google Scholar
[5] Atzeni S, Meyer-ter-Vehn J 2004 The Physics of Inertial Fusion: Beam Plasma Interaction, Hydrodynamics, Hot Dense Matter (Oxford: Oxford University Press) pp198–252
[6] Zhou C D, Betti R 2007 Phys. Plasmas 14 072703
Google Scholar
[7] Rayleigh L 1883 Proc. London Math. Soc. s1 170
Google Scholar
[8] Taylor G 1950 Proc. R. Soc. London: Ser. A 201 192
Google Scholar
[9] Lindl J D, Mead W C 1975 Phys. Rev. Lett. 34 1273
Google Scholar
[10] Takabe H, Mima K, Montierth L, Morse R L 1985 Phys. Fluids 28 3676
Google Scholar
[11] Igumenshchev I V, Velikovich A L, Goncharov V N, Betti R, Campbell E M, Knauer J P, Regan S P, Schmitt A J, Shah R C, Shvydky A 2019 Phys. Rev. Lett. 123 065001
Google Scholar
[12] Peterson J L, Clark D S, Masse L P, Suter L J 2014 Phys. Plasmas 21 092710
Google Scholar
[13] Miller S C, Goncharov V N 2022 Phys. Plasmas 29 082701
Google Scholar
[14] Harding D R, Shmayda W T 2013 Fusion Sci. Technol. 63 125
Google Scholar
[15] Richtmyer R D 1960 Commun. Pure Appl. Math. 13 297
Google Scholar
[16] Meshkov E E 1969 Fluid Dyn. 4 101
Google Scholar
[17] Wouchuk J G, Nishihara K 1997 Phys. Plasmas 4 1028
Google Scholar
[18] Wouchuk J G 2001 Phys. Rev. E 63 056303
Google Scholar
[19] Wouchuk J G 2001 Phys. Plasmas 8 2890
Google Scholar
[20] Campos F C, Wouchuk J G 2016 Phys. Rev. E 93 053111
Google Scholar
[21] Campos F C, Wouchuk J G 2017 Phys. Rev. E 96 013102
Google Scholar
[22] Pickworth L A, Hammel B A, Smalyuk V A, Robey H F, Benedetti L R, Berzak Hopkins L, Bradley D K, Field J E, Haan S W, Hatarik R, Hartouni E, Izumi N, Johnson S, Khan S, Lahmann B, Landen O L, Le Pape S, MacPhee A G, Meezan N B, Milovich J, Nagel S R, Nikroo A, Pak A E, Petrasso R, Remington B A, Rice N G, Springer P T, Stadermann M, Widmann K, Hsing W 2018 Phys. Plasmas 25 054502
Google Scholar
[23] Collins T J B, Stoeckl C, Epstein R, Bittle W A, Forrest C J, Glebov V Y, Goncharov V N, Harding D R, Hu S X, Jacobs-Perkins D W, Kosc T Z, Marozas J A, Mileham C, Marshall F J 2022 Phys. Plasmas 29 012703
Google Scholar
[24] Haines B M, Olson R E, Sweet W, Yi S A, Zylstra A B, Bradley P A, Elsner F, Huang H, Jimenez R, Kline J L, Kong C, Kyrala G A, Leeper R J, Paguio R, Pajoom S, Peterson R R, Ratledge M, Rice N 2019 Phys. Plasmas 26 012707
Google Scholar
[25] Haines B M, Sauppe J P, Albright B J, Daughton W S, Finnegan S M, Kline J L, Smidt J M 2022 Phys. Plasmas 29 042704
Google Scholar
[26] Liu Y X, Chen Z, Wang L F, Li Z Y, Wu J F, Ye W H, Li Y J 2023 Phys. Plasmas 30 042704
Google Scholar
[27] Li Z Y, Wang L F, Wu J F, Ye W H 2020 Acta Mech. Sin. 36 789
Google Scholar
[28] Sano T, Ishigure K, Campos F C 2020 Phys. Rev. E 102 013203
Google Scholar
[29] Goncharov V N 1999 Phys. Rev. Lett. 82 2091
Google Scholar
[30] Goncharov V N, Gotchev O V, Vianello E, Boehly T R, Knauer J P, McKenty P W, Radha P B, Regan S P, Sangster T C, Skupsky S, Smalyuk V A, Betti R, McCrory R L, Meyerhofer D D, Cherfils-Clérouin C 2006 Phys. Plasmas 13 012702
Google Scholar
[31] Mikaelian K O 1985 Phys. Rev. A 31 410
Google Scholar
[32] Mikaelian K O 1983 Phys. Rev. A 28 1637
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 2555
- PDF Downloads: 63
- Cited By: 0
