Feynman path-integral strong-field dynamics calculation method

Liu Xi-Wang; Zhang Hong-Dan; Ben Shuai; Yang Shi-Dong; Ren Xin; Song Xiao-Hong; Yang Wei-Feng

doi:10.7498/aps.72.20230451

Abstract

The emergence and development of ultrafast intense lasers and attosecond measurement techniques have made it possible to observe and control the motions of electrons on a timescale of attoseconds and a spatial scale of atoms. With the improvement of experimental measurement accuracy, higher requirements are put forward for the accuracy of theoretical calculation methods. Extracting temporal and spatial information about ultrafast dynamics from experimental results through using theoretical models presents a significant challenge. Compared with the exact solutions of the time-dependent Schrödinger equation, the Feynman path-integral method for strong-field dynamics calculations offers a simpler model and higher computational efficiency. The electronic wave packet is regarded as a particle with different initial states, and by analyzing the motion of the particle, the causes of various nonlinear physical phenomena in strong fields can be clarified. This work introduces the saddle point approximation into strong field dynamics calculations based on the strong field approximation theory. Furthermore, the Coulomb-corrected strong field approximation method, trajectory-based Coulomb-corrected strong field approximation method, and Coulomb quantum trajectory strong field approximation method are presented in detail. This review aims to provide relevant methods and literature references for studying strong field dynamics theoretical calculations and also to present some ideas for developing new algorithms.

Keywords:

Authors and contacts

1.
School of Physics and Optoelectronic engineering, Hainan University, Haikou 570228, China
2.
College of Science, Shantou University, Shantou 515063, China
3.
Center for Theoretical Physics, Hainan University, Haikou 570228, China

Corresponding author: Song Xiao-Hong, song_xiaohong@hainanu.edu.cn ; Yang Wei-Feng, wfyang@hainanu.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 12074240, 12374260, 12204135, 12264013, 12204136), the Natural Science Foundation of Hainan Province, China (Grant Nos. 122CXTD504, 123MS002, 123QN179, 123QN180, 122QN217), and the Sino-German Mobility Programme, China (Grant No. M-0031).

FullText HTML : translate this paragraph

References

[1]	Schrödinger E 1926 Ann. Phys. 79 361
[2]	Born M, Jordan P 1925 Zeit. Phys. 34 858 Google Scholar
[3]	Feynman R P 1948 Rev. Mod. Phys. 20 367 Google Scholar
[4]	Feynman R P, Hibbs A R 1965 Quantum Mechanics and Path Integrals (New York: McGraw Hill Press) p77
[5]	Maiman T H 1960 Nature 187 493 Google Scholar
[6]	Voronov G S, Delone N B 1965 JETP Lett. 1 66
[7]	Agostini P, Barjot G, Bonnal J, Mainfray G, Manus C, Multiphoton J M 1968 IEEE J. Quantum Electron. 4 667 Google Scholar
[8]	Agostini P, Fabre F, Mainfray G, Petite G, Rahman N K 1979 Phys. Rev. Lett. 42 1127 Google Scholar
[9]	Keldysh L V 1965 Sov. Phys. JETP. 20 1307
[10]	Faisal F H M 1973 J. Phys. B: At. Mol. Opt. Phys. 6 L89
[11]	Reiss H R 1980 Phys. Rev. A 22 1786 Google Scholar
[12]	Perelomov A M, Popov V S, Terent’ev M V 1966 Sov. Phys. JETP. 23 924
[13]	Ammosov M V, Delone N B, Krainov V P 1986 Sov. Phys. JETP. 64 1191
[14]	Lewenstein M, Balcou P, Ivanov M Y, L’ Huillier A, Corkum P B 1994 Phys. Rev. A 49 2117 Google Scholar
[15]	Mosert V, Bauer D 2016 Comput. Phys. Commun. 207 452 Google Scholar
[16]	Tao L, Scrinzi A 2012 New J. Phys. 14 013021 Google Scholar
[17]	Jain M, Tzoar N 1978 Phys. Rev. A 18 538 Google Scholar
[18]	Duchateau G, Cormier E, Gayet R 2002 Phys. Rev. A 66 023412 Google Scholar
[19]	Yu S G, Wang Y L, Lai X Y, Huang Y Y, Quan W, Liu X J 2016 Phys. Rev. A 94 033418 Google Scholar
[20]	Yudin G L, Chelkowski S, Bandrauk A D 2006 J. Phys. B: At. Mol. Opt. Phys. 39 L17 Google Scholar
[21]	Popruzhenko S V, Paulus G G, Bauer D 2008 Phys. Rev. A 77 053409 Google Scholar
[22]	Popruzhenko S V, Bauer D 2008 J. Mod. Optic. 55 2573 Google Scholar
[23]	Yan T M, Popruzhenko S V, Vrakking M J J, Bauer D 2010 Phys. Rev. Lett. 105 253002 Google Scholar
[24]	Yan T M, Bauer D 2012 Phys. Rev. A 86 053403 Google Scholar
[25]	Lai X Y, Poli C, Schomerus H, Figueira de Morisson Faria C 2015 Phys. Rev. A 92 043407 Google Scholar
[26]	Lai X Y, Yu S G, Huang Y Y, Hua L Q, Gong C, Quan W, Figueira de Morisson Faria C, Liu X J 2017 Phys. Rev. A 96 013414 Google Scholar
[27]	Corkum P B, Burnett N H, Brunel F 1989 Phys. Rev. Lett. 62 1259 Google Scholar
[28]	Salières P, L’Huillier A, Lewenstein M 1995 Phys. Rev. Lett. 74 3776 Google Scholar
[29]	Salières P, Carré B, Le Déroff L, Grasbon F, Paulus G G, Walther H, Kopold R, Becker W, Milosÿevic D B 2001 Science 292 902 Google Scholar
[30]	Huismans Y, Rouzée A, Gijsbertsen A, Jungmann J H, Smolkowska A S, Logan P S W M, Lépine F, Cauchy C, Zamith S, Marchenko T, Bakker J M, Berden G, Redlich B, Van Der Meer A F G, Muller H G, Vermin W, Schafer K J, Spanner M, Ivanov M Y U, Smirnova O, Bauer D, Porruzhenko S V, Vrakking M J J 2011 Science 331 61 Google Scholar
[31]	Li M, Geng J W, Liu H, Deng Y, Wu C Y, Peng L Y, Gong Q H, Liu Y Q 2014 Phys. Rev. Lett. 112 113002 Google Scholar
[32]	Hu B, Liu J, Chen S 1997 Phys. Lett. A. 236 533 Google Scholar
[33]	Shvetsov-Shilovski N I, Lein M, Madsen L B, Räsänen E, Lemell C, Burgdörfer J, Arbó D G, Tókési K 2016 Phys. Rev. A 94 013415 Google Scholar
[34]	Song X, Lin C, Sheng Z H, Liu P, Chen Z J, Yang W F, Hu S L, Lin C D, Chen J 2016 Sci. Rep. 6 28392 Google Scholar
[35]	Liu M M, Li M, Wu C Y, Gong Q H, André Staudte, Liu Y Q 2016 Phys. Rev. Lett. 116 163004 Google Scholar
[36]	Liu M M, Liu Y Q 2017 J. Phys. B: At. Mol. Opt. Phys. 50 105602 Google Scholar
[37]	Gong X C, Lin C, He F, Song Q Y, Lin K, Ji Q Y, Zhang W B, Ma J Y, Lu P F, Liu Y Q, Zeng H P, Yang W F, Wu J 2017 Phys. Rev. Lett. 118 143203 Google Scholar
[38]	Song X H, Shi G L, Zhang G J, Xu J W, Lin C, Chen J, Yang W F 2018 Phys. Rev. Lett. 121 103201 Google Scholar
[39]	Porat G, Alon G, Rozen S, Pedatzur O, Krüger M, Azoury D, Natan A, Orenstein G, Bruner B D, Vrakking M J J, Dudovich N 2018 Nat. Commun. 9 2805 Google Scholar
[40]	Trabert D, Brennecke S, Fehre K, Anders N, Geyer A, Grundmann S, Schöffler M S, Schmidt L Ph H, Jahnke T, Dörner R, Kunitski M, Eckart S 2021 Nat. Commun. 12 1697 Google Scholar
[41]	Torlina L, Morales F, Kaushal J, Ivanov I, Kheifets A, Zielinski A, Scrinzi A, Muller H G, Sukiasyan S, Ivanov M Smirnova O 2015 Nat. Phys. 11 503 Google Scholar
[42]	Tong J H, Liu X W, Dong W H, Jiang W Y, Zhu M, Xu Y D, Zuo Z T, Lu P F, Gong X C, Song X H, Yang W F, Wu J 2022 Phys. Rev. Lett. 129 173201 Google Scholar
[43]	Scully M O, Zubairy M S 1997 Quantum Optics (Cambridge: Cambridge University Press) pp146–149
[44]	Bauer D, Milošević D B, Becker W 2005 Phys. Rev. A 72 023415 Google Scholar
[45]	Bleistein N, Handelsman R A 1986 Asymptotic Expansions of Integrals (Dover: Dover Publications) p252
[46]	Booth A D 1949 J. Mech. Appl. Math. 2 460 Google Scholar
[47]	Booth A D 1947 Nature 160 196 Google Scholar
[48]	Huang L, Wu T 2018 Theor. Biol. Med. Modell. 15 22 Google Scholar
[49]	Lai X Y, Figueira de Morisson Faria C 2013 Phys. Rev. A 88 013406 Google Scholar
[50]	Maxwell A S 2019 Ph. D. Dissertation (London: University College London
[51]	Yang S D, Song X H, Liu X W, Zhang H D, Shi G L, Yu X H, Tang Y J, Chen J, Yang W F 2020 Laser Phys. Lett. 17 095301 Google Scholar
[52]	Becker W, Grasbon F, Kopold R, Milošević D B, Paulus G G, Walther H 2002 Adv. At. Mol. Opt. Phys. 48 35 Google Scholar
[53]	Paul M, Gräfe S 2019 Phys. Rev. A 99 053414 Google Scholar
[54]	Liu M M, Shao Y, Han M, Ge P P, Deng Y K, Wu C Y, Gong Q H, Liu Y Q 2018 Phys. Rev. Lett. 120 043201 Google Scholar
[55]	Yan T M 2012 Ph. D. Dissertation (Germany: Universität Rostock
[56]	Arbó D G, Ishikawa K L, Persson E, Burgdörfer J 2012 Nucl. Instrum. Methods Phys. Res. , Sect. B 279 24 Google Scholar
[57]	Milošević D B, Paulus G G, Bauer D, Becker W 2006 J. Phys. B: At. Mol. Opt. Phys. 39 R203 Google Scholar
[58]	Becker A, Faisal F H M 2005 J. Phys. B: At. Mol. Opt. Phys. 38 R1 Google Scholar
[59]	Popov V S 2004 Phys. Usp. 47 855 Google Scholar
[60]	Xiao X R, Wang M X, Xiong W H, Peng L Y 2016 Phys. Rev. E 94 053310 Google Scholar
[61]	李庆扬, 王能超, 易大义 2008 数值分析(第五版) (北京: 清华大学出版社) 第286页 Li Q Y, Wang N C, Yi D Y 2008 Numerical Analysis (5th Ed.) (Beijing: Tsinghua University Press) p286
[62]	Shvetsov-Shilovski N I, Goreslavski S P, Popruzhenko S V, Becker W 2009 Laser Phys. 19 1550 Google Scholar
[63]	Shvetsov-Shilovski N I, Dimitrovski D, Madsen L B 2012 Phys. Rev. A 85 023428 Google Scholar

Cited By

图 1 遗传算法流程图

Figure 1. Flowchart of genetic algorithm.

DownLoad: Full-Size Img PowerPoint

图 2 牛顿迭代法图示. 蓝色曲线为方程$ f\left(x\right) $的解, 红色直线为蓝色曲线在自变量$ x $处的切线, $ {x}_{*} $为方程$ f\left(x\right)=0 $时需寻找的解

Figure 2. Illustration of Newton’s method. Blue curve represents value of function $ f\left(x\right) $, and red lines represent tangent to blue curve at independent variable $ x $, which is solution $ {x}_{*} $ when $ f\left(x\right)=0 $.

DownLoad: Full-Size Img PowerPoint

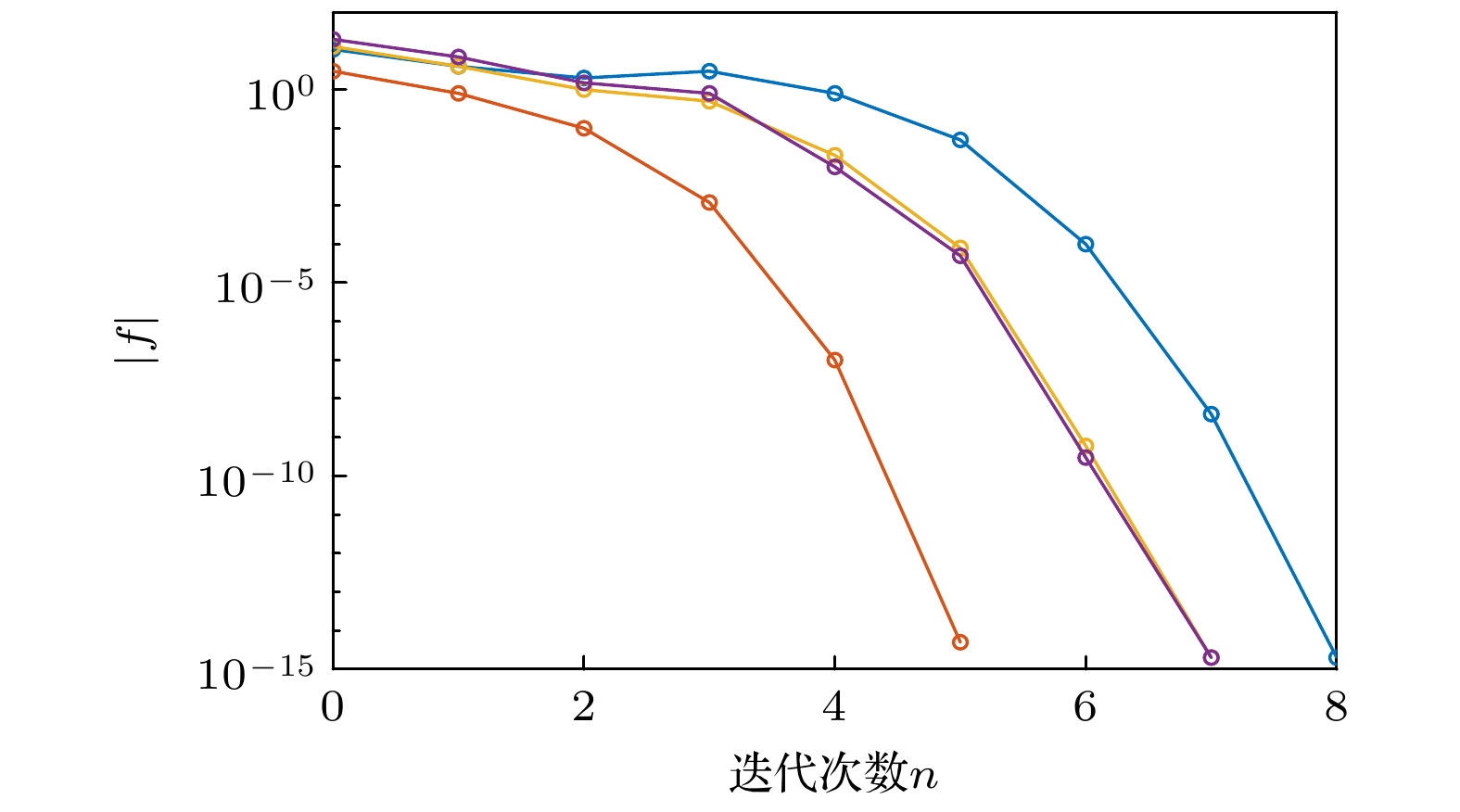
图 3 4个样本的$ \left|f\right| $随迭代次数的变化. 蓝线、橙线、黄线和紫线分别代表初始试探解为$ ({t}_{{\rm{r}}}=20.1, {t}_{{\rm{i}}}=80.1) $、$ ({t}_{{\rm{r}}}= $$ 40.1, {t}_{{\rm{i}}}=80.1) $, $ ({t}_{{\rm{r}}}=60.1, {t}_{{\rm{i}}}=80.1) $和$ ({t}_{{\rm{r}}}=120.1, {t}_{{\rm{i}}}= $$ 80.1) $时, 随迭代次数增加函数值$ \left|f\right| $的变化.

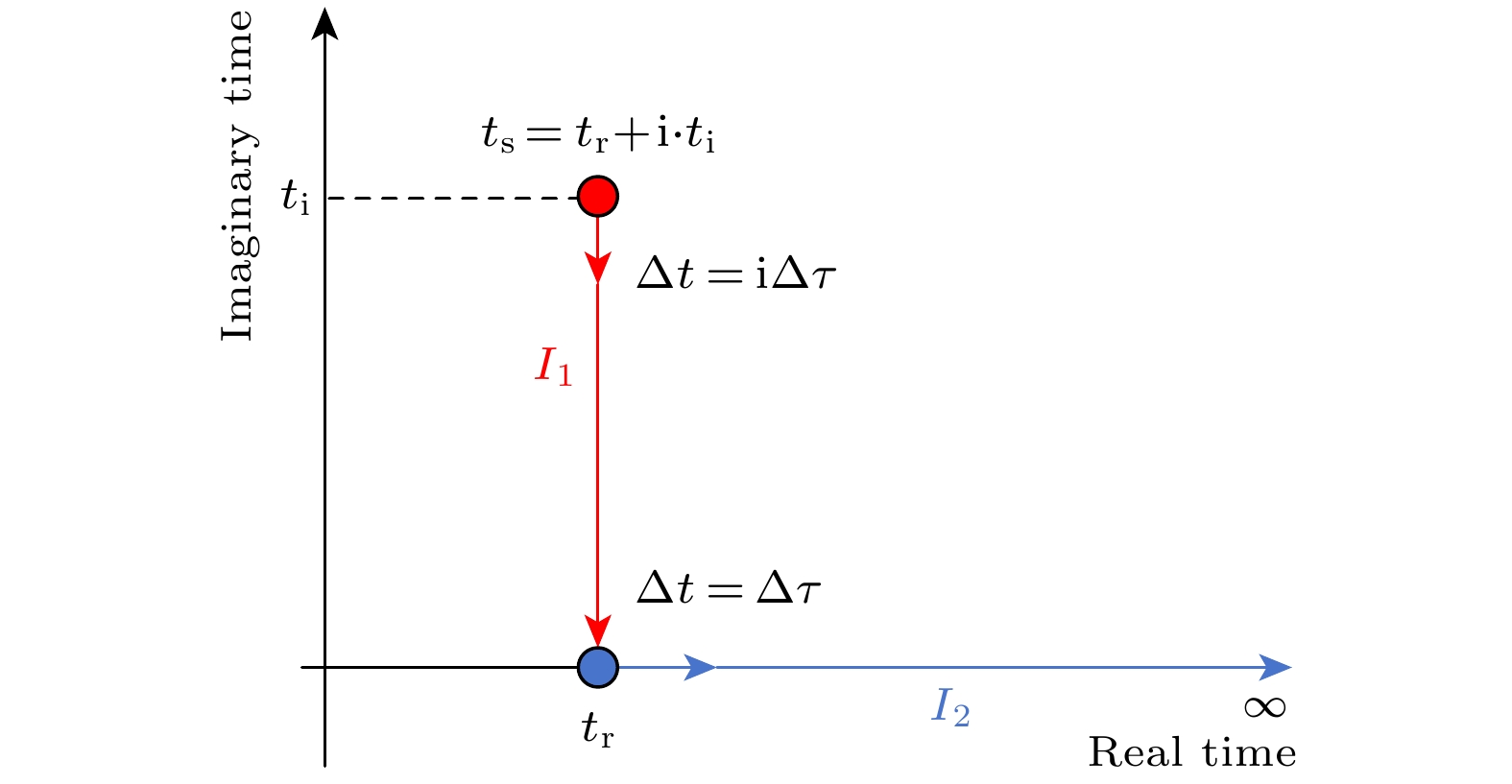
Figure 3. Variation of $ \left|f\right| $ with the number of iterations n for four samples. The blue, orange, yellow, and purple lines represent the changes in function values $ \left|f\right| $ with increasing iteration times when the initial trial solutions are $ ({t}_{{\rm{r}}}=20.1, {t}_{{\rm{i}}}=80.1) $, $ ({t}_{{\rm{r}}}=40.1, {t}_{{\rm{i}}}=80.1) $, $ ({t}_{{\rm{r}}}=60.1, $$ {t}_{{\rm{i}}}= 80.1) $ and $ ({t}_{{\rm{r}}}=120.1, {t}_{{\rm{i}}}=80.1) $, respectively.

DownLoad: Full-Size Img PowerPoint

图 4 复平面的路径积分. $ {I}_{1} $ 描述了沿虚时间轴的积分, 步长为 $ {\rm{i}}\Delta \tau $. $ {I}_{2} $ 描述了沿实时间轴的积分, 步长为$ \Delta \tau $

Figure 4. Path integral on complex plane. $ {I}_{1} $ describes integration along imaginary time axis with a step size of $ {\rm{i}}\Delta \tau $, and $ {I}_{2} $ describes the integration along real time axis with a step size of $ \Delta \tau $.

DownLoad: Full-Size Img PowerPoint

图 5 费曼路径积分思想示意图. A与B分别为粒子的初始点与末点, 绿色虚线为粒子的可能路径　(a) 两个位置之间存在一个挡板双缝; (b) 两个位置间存在两个多缝挡板; (c) 两个位置存在无数个狭缝, 此时粒子可以从A点经历任意位置到达B点

Figure 5. Schematic diagram of Feynman’s path integral concept. A and B represent initial and final points of a particle, and the green dashed line represents the possible paths of particle: (a) There is a double-slit barrier between two positions; (b) there are multiple slit barriers between two positions; (c) there are infinite slits between two positions, and particle can reach point B from point A through any intermediate position.

DownLoad: Full-Size Img PowerPoint

图 6 $ {p}_{z} $-$ {p}_{x} $平面内光电子动量分布图^[24]　(a) TDSE, (b) SFA, (c) TCSFA不考虑势垒下作用量; (d) TCSFA 考虑势垒下作用量

Figure 6. Logarithmically scaled photoelectron momentum distribution in $ {p}_{z} $-$ {p}_{x} $ plane^[24]: (a) TDSE, (b) SFA and (c) TCSFA without sub-CC; (d) TCSFA with sub-CC.

DownLoad: Full-Size Img PowerPoint

图 7 氢原子二维光电子角度分布^[26]　(a) CQSFA; (b) SFA; (c) TDSE

Figure 7. Two-dimensional photoelectron angular distributions of hydrogen atom^[26]: (a) CQSFA; (b) SFA; (c) TDSE.

DownLoad: Full-Size Img PowerPoint

map

[1]	Schrödinger E 1926 Ann. Phys. 79 361
[2]	Born M, Jordan P 1925 Zeit. Phys. 34 858 Google Scholar
[3]	Feynman R P 1948 Rev. Mod. Phys. 20 367 Google Scholar
[4]	Feynman R P, Hibbs A R 1965 Quantum Mechanics and Path Integrals (New York: McGraw Hill Press) p77
[5]	Maiman T H 1960 Nature 187 493 Google Scholar
[6]	Voronov G S, Delone N B 1965 JETP Lett. 1 66
[7]	Agostini P, Barjot G, Bonnal J, Mainfray G, Manus C, Multiphoton J M 1968 IEEE J. Quantum Electron. 4 667 Google Scholar
[8]	Agostini P, Fabre F, Mainfray G, Petite G, Rahman N K 1979 Phys. Rev. Lett. 42 1127 Google Scholar
[9]	Keldysh L V 1965 Sov. Phys. JETP. 20 1307
[10]	Faisal F H M 1973 J. Phys. B: At. Mol. Opt. Phys. 6 L89
[11]	Reiss H R 1980 Phys. Rev. A 22 1786 Google Scholar
[12]	Perelomov A M, Popov V S, Terent’ev M V 1966 Sov. Phys. JETP. 23 924
[13]	Ammosov M V, Delone N B, Krainov V P 1986 Sov. Phys. JETP. 64 1191
[14]	Lewenstein M, Balcou P, Ivanov M Y, L’ Huillier A, Corkum P B 1994 Phys. Rev. A 49 2117 Google Scholar
[15]	Mosert V, Bauer D 2016 Comput. Phys. Commun. 207 452 Google Scholar
[16]	Tao L, Scrinzi A 2012 New J. Phys. 14 013021 Google Scholar
[17]	Jain M, Tzoar N 1978 Phys. Rev. A 18 538 Google Scholar
[18]	Duchateau G, Cormier E, Gayet R 2002 Phys. Rev. A 66 023412 Google Scholar
[19]	Yu S G, Wang Y L, Lai X Y, Huang Y Y, Quan W, Liu X J 2016 Phys. Rev. A 94 033418 Google Scholar
[20]	Yudin G L, Chelkowski S, Bandrauk A D 2006 J. Phys. B: At. Mol. Opt. Phys. 39 L17 Google Scholar
[21]	Popruzhenko S V, Paulus G G, Bauer D 2008 Phys. Rev. A 77 053409 Google Scholar
[22]	Popruzhenko S V, Bauer D 2008 J. Mod. Optic. 55 2573 Google Scholar
[23]	Yan T M, Popruzhenko S V, Vrakking M J J, Bauer D 2010 Phys. Rev. Lett. 105 253002 Google Scholar
[24]	Yan T M, Bauer D 2012 Phys. Rev. A 86 053403 Google Scholar
[25]	Lai X Y, Poli C, Schomerus H, Figueira de Morisson Faria C 2015 Phys. Rev. A 92 043407 Google Scholar
[26]	Lai X Y, Yu S G, Huang Y Y, Hua L Q, Gong C, Quan W, Figueira de Morisson Faria C, Liu X J 2017 Phys. Rev. A 96 013414 Google Scholar
[27]	Corkum P B, Burnett N H, Brunel F 1989 Phys. Rev. Lett. 62 1259 Google Scholar
[28]	Salières P, L’Huillier A, Lewenstein M 1995 Phys. Rev. Lett. 74 3776 Google Scholar
[29]	Salières P, Carré B, Le Déroff L, Grasbon F, Paulus G G, Walther H, Kopold R, Becker W, Milosÿevic D B 2001 Science 292 902 Google Scholar
[30]	Huismans Y, Rouzée A, Gijsbertsen A, Jungmann J H, Smolkowska A S, Logan P S W M, Lépine F, Cauchy C, Zamith S, Marchenko T, Bakker J M, Berden G, Redlich B, Van Der Meer A F G, Muller H G, Vermin W, Schafer K J, Spanner M, Ivanov M Y U, Smirnova O, Bauer D, Porruzhenko S V, Vrakking M J J 2011 Science 331 61 Google Scholar
[31]	Li M, Geng J W, Liu H, Deng Y, Wu C Y, Peng L Y, Gong Q H, Liu Y Q 2014 Phys. Rev. Lett. 112 113002 Google Scholar
[32]	Hu B, Liu J, Chen S 1997 Phys. Lett. A. 236 533 Google Scholar
[33]	Shvetsov-Shilovski N I, Lein M, Madsen L B, Räsänen E, Lemell C, Burgdörfer J, Arbó D G, Tókési K 2016 Phys. Rev. A 94 013415 Google Scholar
[34]	Song X, Lin C, Sheng Z H, Liu P, Chen Z J, Yang W F, Hu S L, Lin C D, Chen J 2016 Sci. Rep. 6 28392 Google Scholar
[35]	Liu M M, Li M, Wu C Y, Gong Q H, André Staudte, Liu Y Q 2016 Phys. Rev. Lett. 116 163004 Google Scholar
[36]	Liu M M, Liu Y Q 2017 J. Phys. B: At. Mol. Opt. Phys. 50 105602 Google Scholar
[37]	Gong X C, Lin C, He F, Song Q Y, Lin K, Ji Q Y, Zhang W B, Ma J Y, Lu P F, Liu Y Q, Zeng H P, Yang W F, Wu J 2017 Phys. Rev. Lett. 118 143203 Google Scholar
[38]	Song X H, Shi G L, Zhang G J, Xu J W, Lin C, Chen J, Yang W F 2018 Phys. Rev. Lett. 121 103201 Google Scholar
[39]	Porat G, Alon G, Rozen S, Pedatzur O, Krüger M, Azoury D, Natan A, Orenstein G, Bruner B D, Vrakking M J J, Dudovich N 2018 Nat. Commun. 9 2805 Google Scholar
[40]	Trabert D, Brennecke S, Fehre K, Anders N, Geyer A, Grundmann S, Schöffler M S, Schmidt L Ph H, Jahnke T, Dörner R, Kunitski M, Eckart S 2021 Nat. Commun. 12 1697 Google Scholar
[41]	Torlina L, Morales F, Kaushal J, Ivanov I, Kheifets A, Zielinski A, Scrinzi A, Muller H G, Sukiasyan S, Ivanov M Smirnova O 2015 Nat. Phys. 11 503 Google Scholar
[42]	Tong J H, Liu X W, Dong W H, Jiang W Y, Zhu M, Xu Y D, Zuo Z T, Lu P F, Gong X C, Song X H, Yang W F, Wu J 2022 Phys. Rev. Lett. 129 173201 Google Scholar
[43]	Scully M O, Zubairy M S 1997 Quantum Optics (Cambridge: Cambridge University Press) pp146–149
[44]	Bauer D, Milošević D B, Becker W 2005 Phys. Rev. A 72 023415 Google Scholar
[45]	Bleistein N, Handelsman R A 1986 Asymptotic Expansions of Integrals (Dover: Dover Publications) p252
[46]	Booth A D 1949 J. Mech. Appl. Math. 2 460 Google Scholar
[47]	Booth A D 1947 Nature 160 196 Google Scholar
[48]	Huang L, Wu T 2018 Theor. Biol. Med. Modell. 15 22 Google Scholar
[49]	Lai X Y, Figueira de Morisson Faria C 2013 Phys. Rev. A 88 013406 Google Scholar
[50]	Maxwell A S 2019 Ph. D. Dissertation (London: University College London
[51]	Yang S D, Song X H, Liu X W, Zhang H D, Shi G L, Yu X H, Tang Y J, Chen J, Yang W F 2020 Laser Phys. Lett. 17 095301 Google Scholar
[52]	Becker W, Grasbon F, Kopold R, Milošević D B, Paulus G G, Walther H 2002 Adv. At. Mol. Opt. Phys. 48 35 Google Scholar
[53]	Paul M, Gräfe S 2019 Phys. Rev. A 99 053414 Google Scholar
[54]	Liu M M, Shao Y, Han M, Ge P P, Deng Y K, Wu C Y, Gong Q H, Liu Y Q 2018 Phys. Rev. Lett. 120 043201 Google Scholar
[55]	Yan T M 2012 Ph. D. Dissertation (Germany: Universität Rostock
[56]	Arbó D G, Ishikawa K L, Persson E, Burgdörfer J 2012 Nucl. Instrum. Methods Phys. Res. , Sect. B 279 24 Google Scholar
[57]	Milošević D B, Paulus G G, Bauer D, Becker W 2006 J. Phys. B: At. Mol. Opt. Phys. 39 R203 Google Scholar
[58]	Becker A, Faisal F H M 2005 J. Phys. B: At. Mol. Opt. Phys. 38 R1 Google Scholar
[59]	Popov V S 2004 Phys. Usp. 47 855 Google Scholar
[60]	Xiao X R, Wang M X, Xiong W H, Peng L Y 2016 Phys. Rev. E 94 053310 Google Scholar
[61]	李庆扬, 王能超, 易大义 2008 数值分析(第五版) (北京: 清华大学出版社) 第286页 Li Q Y, Wang N C, Yi D Y 2008 Numerical Analysis (5th Ed.) (Beijing: Tsinghua University Press) p286
[62]	Shvetsov-Shilovski N I, Goreslavski S P, Popruzhenko S V, Becker W 2009 Laser Phys. 19 1550 Google Scholar
[63]	Shvetsov-Shilovski N I, Dimitrovski D, Madsen L B 2012 Phys. Rev. A 85 023428 Google Scholar

[1]	Feng Bo, Xu Wen-Jun, Cai Jie-Xiong, Wu Ru-Shan, Wang Hua-Zhong. Phase-preserving theory and its linearization approximation for forward scattering field of scalar acoustic wave equation. Acta Physica Sinica, 2023, 72(15): 159101. doi: 10.7498/aps.72.20230194
[2]	Zang Yu-Chen, Su Chang, Wu Peng-Fei, Lin Wei-Jun. Born approximation of acoustic radiation force and torque for an arbitrary particle in a zero-order standing Bessel beam. Acta Physica Sinica, 2022, 71(10): 104302. doi: 10.7498/aps.71.20212251
[3]	Ma Chuang, Yang Xiao-Long, Chen Han-Shuang, Zhang Hai-Feng. A mean-field approximation based BP algorithm for solving the stochastic block model. Acta Physica Sinica, 2021, 70(22): 228901. doi: 10.7498/aps.70.20210511
[4]	Zhu Yan-Ju, Jiang Yue-Song, Hua Hou-Qiang, Zhang Chong-Hui, Xin Can-Wei. Modified equivalent current approximation and graphical electromagnetic computing method of analyzing radar cross section of missile target scatterer covered with thermal protection layer. Acta Physica Sinica, 2014, 63(24): 244101. doi: 10.7498/aps.63.244101
[5]	Liu Hao-Di. Berry phase and Hannay's angle of an electromagnetic mode system driven by harmonic field with Born-Oppenheimer approximation. Acta Physica Sinica, 2013, 62(10): 100302. doi: 10.7498/aps.62.100302
[6]	Jiao Xiao-Yu. The approximate homotopy symmetry reduction for far-field model equation. Acta Physica Sinica, 2011, 60(12): 120201. doi: 10.7498/aps.60.120201
[7]	Cheng Chun-Zhi, Zhou Xiao-Xin, Li Peng-Cheng. The wavelength dependence of high-order harmonic generationand attosecond pulses from atom in infrared laser field. Acta Physica Sinica, 2011, 60(3): 033203. doi: 10.7498/aps.60.033203
[8]	Liao Xu, Cong Hong-Lu, Jiang Dao-Lai, Ren Xue-Zao. Influence of the field with varying frequency modulation on atomic population inversion in non-ratating-wave approximation. Acta Physica Sinica, 2010, 59(8): 5508-5513. doi: 10.7498/aps.59.5508
[9]	Yang Pei, Chen Yong, Li Zhi-Bin. Analytic approximation for the soliton solution of the discrete modified KdV equation. Acta Physica Sinica, 2010, 59(6): 3668-3673. doi: 10.7498/aps.59.3668
[10]	Guo Zhong-Hua, Zhou Xiao-Xin. The influence of molecular ground state wave function on high-order harmonic generation from N2 molecules in intense laser fields. Acta Physica Sinica, 2008, 57(3): 1616-1621. doi: 10.7498/aps.57.1616
[11]	Mo Jia-Qi, Zhang Wei-Jiang, He Ming. The solitary wave approximate solution of strongly nonlinear evolution equations. Acta Physica Sinica, 2007, 56(4): 1843-1846. doi: 10.7498/aps.56.1843
[12]	Wu Ye, Xiao Jing-Hua, Zhan Meng. Approximate synchronization of strongly coupled chaotic systems. Acta Physica Sinica, 2007, 56(9): 5119-5123. doi: 10.7498/aps.56.5119
[13]	Jia Fei, Xie Shuang-Yuan, Yang Ya-Ping. Interaction of an atom with a field with varying frequency without rotating-wave approximation. Acta Physica Sinica, 2006, 55(11): 5835-5841. doi: 10.7498/aps.55.5835
[14]	Liu Chun-Xiang, Cheng Chuan-Fu, Ren Xiao-Rong, Liu Man, Teng Shu-Yun, Xu Zhi-Zhan. Green's function method of light scattering from random surfaces compares with Kirchhoff's approximation. Acta Physica Sinica, 2004, 53(2): 427-435. doi: 10.7498/aps.53.427
[15]	Zhang Cheng-Hua, Qian Wen-Jia, Leng Wen-Xiu, Li Jun-Xia, Long Qi-Wei, Tian En-Ke. . Acta Physica Sinica, 2002, 51(10): 2225-2228. doi: 10.7498/aps.51.2225
[16]	FANG MAO-FA. EVOLUTION OF THE FIELD ENTROPY IN JAYNES-CUMMINGS MODEL WITHOUT ROTATING-WAVE APPROXIMATION. Acta Physica Sinica, 1994, 43(11): 1776-1786. doi: 10.7498/aps.43.1776
[17]	LI GAO-XIANG, PENG JIN-SHENG. PHASE FLUCTUATIONS IN JAYNES-CUMMINGS MODEL WITH AND WITHOUT ROTATION WAVE APPROXIMATION. Acta Physica Sinica, 1992, 41(5): 766-773. doi: 10.7498/aps.41.766
[18]	WEI GUO-ZHU, NIE HUI-QUAN, ZHANG KAI-YI. LOCAL APPROACH IN THE HUBBARD MODEL. Acta Physica Sinica, 1988, 37(1): 87-94. doi: 10.7498/aps.37.87
[19]	SU ZHAO-BING, YU LU, ZHOU GUANG-ZHAO. THE GENERALIZED MEAN FIELD EXPANSIONS FOR MANY FERMION SYSTEMS. Acta Physica Sinica, 1984, 33(7): 999-1007. doi: 10.7498/aps.33.999
[20]	. . Acta Physica Sinica, 1966, 22(4): 510-514. doi: 10.7498/aps.22.510

Catalog

Vol. 72, Issue 19 - 2023-10-05

Metrics

Abstract views: 3991
PDF Downloads: 180
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板