A method of modeling saddle point movement driven by multiple radio frequency fields

MAI Jun; WANG Zhao; YUAN Chang; XIAO Jie; MA Wei; WANG Xu

doi:10.7498/aps.74.20241552

Abstract

In an integrated ion trap with integrated optical modules, the problem of misalignment between the optical focus and the trapped ion saddle point is very likely to occur, which seriously hinders the practicality of the experimental method. To solve this problem, the multi-RF field method can be used to compensate for and move the ion saddle point position. However, in the actual experimental process, the application of the multi-RF method requires the knowledge of the amplitude of the RF voltage to be loaded corresponding to the actual spatial position of the saddle point. Therefore, a set of mathematical models is established to describe the relationship. The accuracy of the model determines the control accuracy of the spatial position of the saddle point, and the simplicity of the model determines the speed of the solution process. Therefore, in this work, a mathematical model of the relationship between the multi-RF electric field voltage and the saddle point position is proposed based on the numerically simulated electric field distribution and the polynomial fitting method. It can quickly and accurately give a mathematical description between the two without considering the physical mechanism or model. Numerical method is adopted to verify and discuss the correctness and scope of application of the model, and can quickly and accurately provide the amplitude of the RF voltage to be loaded in the experiment, causing the saddle point to move and coincide with the optical focus. This method greatly reduces the time delay caused by the solution and improves the feedback loop bandwidth during the movement of the saddle point position.

Keywords:

Authors and contacts

1.
College of Big Data and Information Engineering, Guizhou University, Guiyang 550025, China
2.
Shenzhen Institute for Quantum Science and Engineering, Southern University of Science and Technology, Shenzhen 518055, China
3.
International Quantum Academy, Shenzhen 518048, China
4.
Key Laboratory of Advanced Manufacturing Technology, Ministry of Education, Guiyang 550025, China

Corresponding author: WANG Zhao, joeshardow@gmail.com ; WANG Xu, xuwang@gzu.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 12474422, 11904423), the 100-level Selection and Training of High-level Innovative Talents of Guizhou Province, China (Grant No. GCC[2023]090), and the Basic and Applied Basic Research Foundation of Guangdong Province, China (Grant No. 2020A1515010864).

FullText HTML

References

[1]	Siverns J D, Quraishi Q 2017 Quantum Inf. Process. 16 314 Google Scholar
[2]	Ding X Y, Yu Q, Lu X Q, Wang X H, Huo X M, Qian X 2023 Anal. Chem. 95 2348 Google Scholar
[3]	Papanastasiou D, Kounadis D, Lekkas A, et al. 2022 J. Am. Soc. Mass Spectrom. 33 1990 Google Scholar
[4]	Ozawa A, Davila-Rodriguez J, Bounds J R, Schuessler H A, Hänsch T W, Udem T 2017 Nat. Commun. 8 44 Google Scholar
[5]	Amitrano V, Roggero A, Luchi P, Turro F, Vespucci L, Pederiva F 2023 Phys. Rev. D 107 023007 Google Scholar
[6]	Monroe C, Campbell W C, Duan L M, et al. 2021 Rev. Mod. Phys. 93 025001 Google Scholar
[7]	Niroula P, Shaydulin R, Yalovetzky R, Minssen P, Herman D, Hu S, Pistoia M 2022 Sci. Rep. 12 17171 Google Scholar
[8]	Pogorelov I, Feldker T, Marciniak C D, et al. 2021 PRX Quantum 2 020343 Google Scholar
[9]	Wang P P, Luan C Y, Qiao M, Um M, Zhang J H, Wang Y, Yuan X, Gu M L, Zhang J N, Kim K 2021 Nat. Commun. 12 233 Google Scholar
[10]	Manovitz T, Shapira Y, Gazit L, Akerman N, Ozeri R 2022 PRX Quantum 3 010347 Google Scholar
[11]	Mehta K K, Bruzewicz C D, McConnell R, Ram R J, Sage J M, Chiaverini J 2016 Nature Nanotech. 11 1066 Google Scholar
[12]	Ballance C J, Harty T P, Linke N M, Sepiol M A, Lucas D M 2016 Phys. Rev. Lett. 117 060504 Google Scholar
[13]	Rudolph M S, Toussaint N B, Katabarwa A, Johri S, Peropadre B, Perdomo-Ortiz A 2022 Phys. Rev. X 12 031010 Google Scholar
[14]	范桁 2018 67 120301 Google Scholar Fan H 2018 Acta Physica Sinica 67 120301 Google Scholar
[15]	Murali P, Debroy D M, Brown K R, Martonosi M 2022 Commun. ACM 65 101 Google Scholar
[16]	Pino J M, Dreiling J M, Figgatt C, Gaebler J P, Moses S A, Allman M, Baldwin C, Foss-Feig M, Hayes D, Mayer K 2021 Nature 592 209 Google Scholar
[17]	Ivory M, Setzer W J, Karl N, McGuinness H, DeRose C, Blain M, Stick D, Gehl M, Parazzoli L P 2021 Phys. Rev. X 11 041033 Google Scholar
[18]	Malinowski M, Allcock D T C, Ballance C J 2023 PRX Quantum 4 040313 Google Scholar
[19]	Romaszko Z D, Hong S, Siegele M, Puddy R K, Lebrun-Gallagher F R, Weidt S, Hensinger W K 2020 Nat. Rev. Phys. 2 285 Google Scholar
[20]	Wang Y H, Li Y, Yin Z Q, Zeng B 2018 npj Quantum Inf. 4 46 Google Scholar
[21]	Ryan-Anderson C, Bohnet J G, Lee K, et al. 2021 Phys. Rev. X 11 041058 Google Scholar
[22]	Mehta K K, Zhang C, Malinowski M, Nguyen T L, Stadler M, Home J P 2020 Nature 586 533 Google Scholar
[23]	Bao X Y, Cui J M, Fang D, Chen W B, Wang J, Huang Y F, Li C F, Guo G C 2023 JUSTC 53 0705 Google Scholar
[24]	Van Rynbach A, Maunz P, Kim J 2016 Appl. Phys. Lett. 109 221108 Google Scholar
[25]	Wang Z, Wang B R, Ma Q L, Guo J Y, Li M S, Wang Y, Rao X X, Huang Z Q, Luo L 2020 arXiv: 2004.08845 [quant-ph]
[26]	Holz P C, Auchter S, Stocker G, Valentini M, Lakhmanskiy K, Rössler C, Stampfer P, Sgouridis S, Aschauer E, Colombe Y, Blatt R 2020 Adv. Quantum Technol. 3 2000031 Google Scholar
[27]	Liu Y R, Wang Z, Xiang Z X, Wang Q K, Hu T Y, Wang X 2024 Chip 3 100078 Google Scholar
[28]	Hong S, Lee M, Cheon H, Kim T, Cho D I 2016 Sensors 16 616 Google Scholar
[29]	Read F H, Bowring N J 2011 Nucl. Instr. and Meth. A 645 273 Google Scholar
[30]	House M G 2008 Phys. Rev. A 78 033402 Google Scholar
[31]	Lauprêtre T, Achi B, Groult L, Carry É, Kersalé Y, Delehaye M, Hafiz M A, Lacroûte C 2023 Appl. Phys. B 129 37 Google Scholar
[32]	Zhang X, Ou B, Chen T, Xie Y, Wu W, Chen P 2020 Phys. Scr. 95 045103 Google Scholar
[33]	Zhang C, Mehta K K, Home J P 2022 New J. Phys. 24 073030 Google Scholar
[34]	王晨旭, 贺冉, 李睿睿, 陈炎, 房鼎, 崔金明, 黄运锋, 李传锋, 郭光灿 2022 71 133701 Google Scholar Wang C X, He R, Li R R, Chen Y, Fang D, Cui J M, Huang Y F, Li C F, Guo G C 2022 Acta Phys. Sin. 71 133701 Google Scholar
[35]	Kumph M, Holz P, Langer K, Meraner M, Niedermayr M, Brownnutt M, Blatt R 2016 New J. Phys. 18 023047 Google Scholar
[36]	Dehmelt H G 1968 Adv. At. Mol. Phys. 3 53 Google Scholar
[37]	Niedermayr M, Lakhmanskiy K, Kumph M, Partel S, Edlinger J, Brownnutt M, Blatt R 2014 New J. Phys. 16 113068 Google Scholar
[38]	吴宇恺, 段路明 2023 72 230302 Google Scholar Wu Y K, Duan L M 2023 Acta Phys. Sin. 72 230302 Google Scholar

Cited By

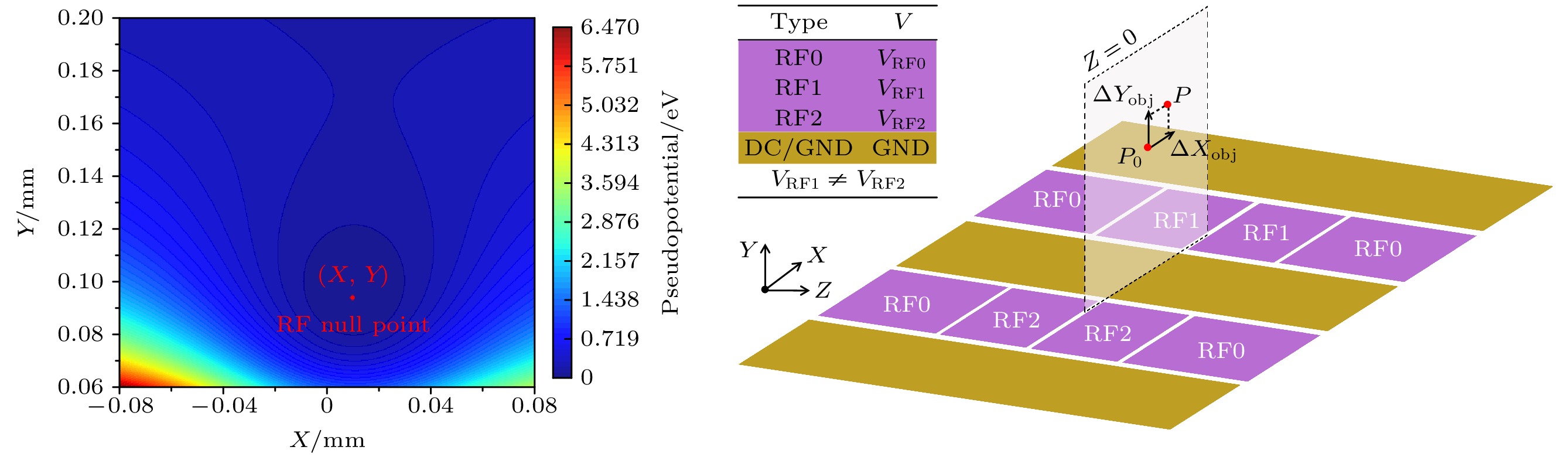
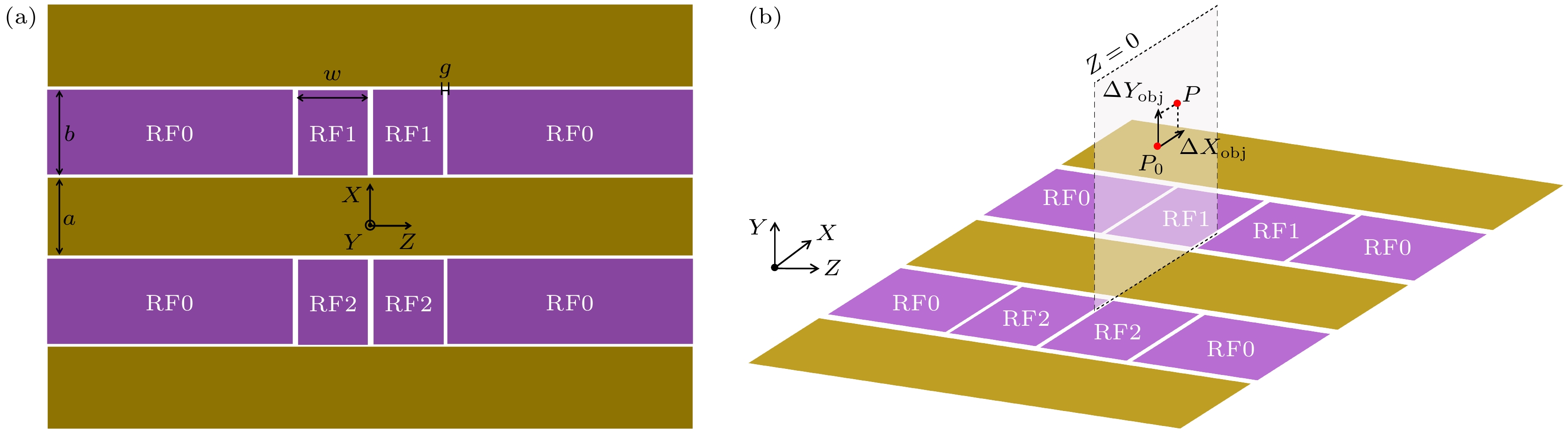
图 1 建立多射频场驱动鞍点移动的基本电极结构　(a) 射频电极经分段处理的表面离子阱结构; (b) 调节多射频电压幅值驱动鞍点径向移动

Figure 1. Establishing the basic electrode structure for multi-RF field driven saddle point movement: (a) Surface ion trap structure after radio frequency electrode segmentation treatment; (b) adjusting the amplitude of multiple RF voltages to drive the radial movement of the saddle point.

DownLoad: Full-Size Img PowerPoint

图 2 赝势分布情况　(a) 研究对象Z = 0处初始赝势分布; (b) 径向面内赝势梯度变化最小方向上的赝势分布

Figure 2. Pseudopotential distribution: (a) Initial pseudopotential distribution on the radial plane Z = 0; (b) pseudopotential distribution in the direction with the smallest pseudopotential gradient change in the radial plane.

DownLoad: Full-Size Img PowerPoint

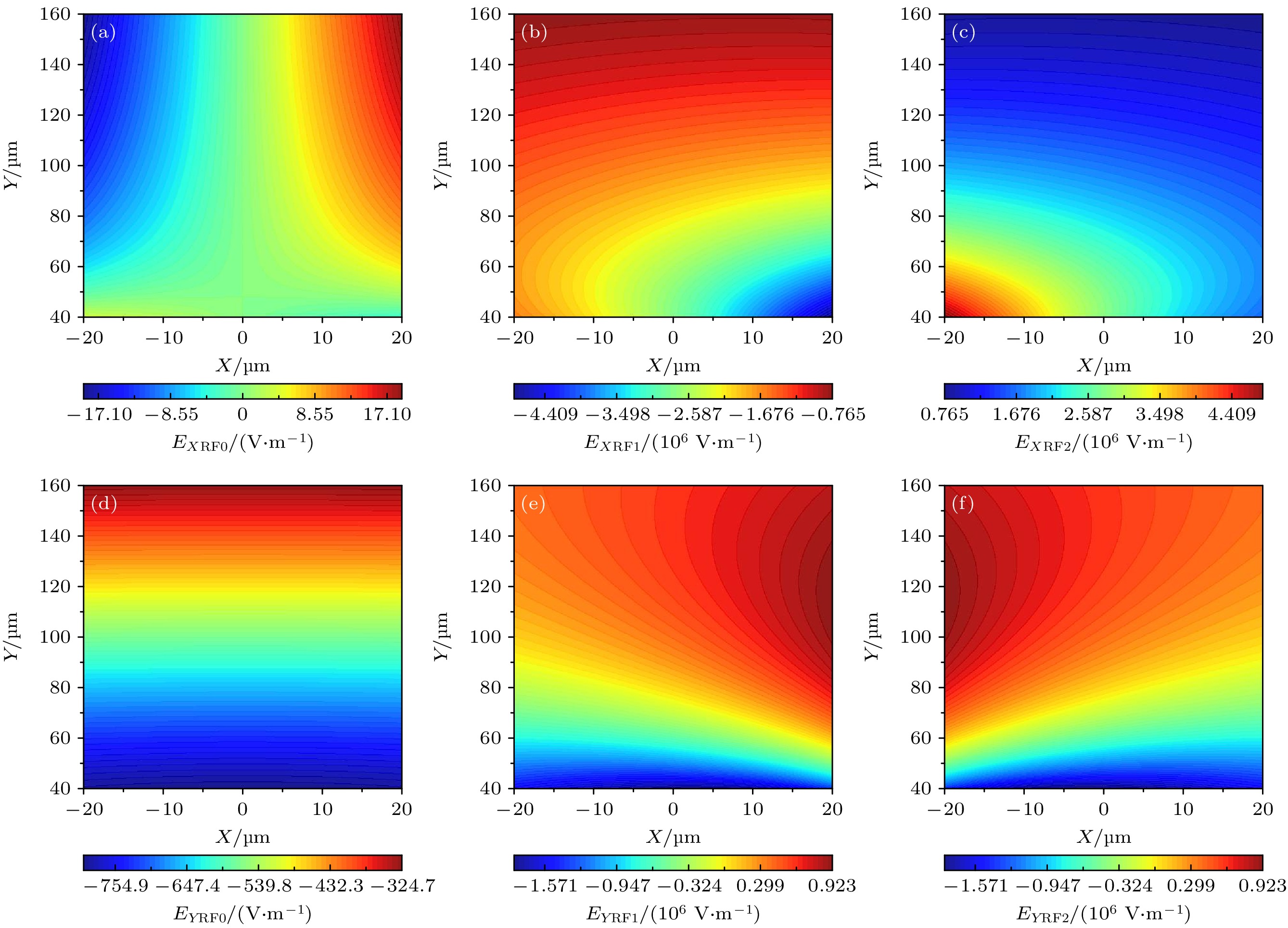
图 3 射频电极组各电极RFi (i = 0—2)依次施加单位电压时, Z = 0处电场分布情况　(a) RF0作用下X方向的电场分布E_XRF0; (b) RF1作用下X方向的电场分布E_XRF1; (c) RF2作用下X方向的电场分布E_XRF2; (d) RF0作用下Y方向的电场分布E_YRF0; (e) RF1作用下Y方向的电场分布E_YRF1; (f) RF2作用下Y方向的电场分布E_YRF2

Figure 3. When unit voltage is applied to each electrode RFi (i = 0—2) of the RF electrode group in turn, the electric field distribution at Z = 0: (a) Electric field distribution E_XRF0 in the X direction under the action of electrode RF0; (b) electric field distribution E_XRF1 in the X direction under the action of electrode RF1; (c) electric field distribution E_XRF2 in the X direction under the action of electrode RF2; (d) electric field distribution in the Y direction under the action of electrode RF0; (e) electric field distribution in the Y direction under the action of electrode RF1; (f) electric field distribution in the Y direction under the action of electrode RF2.

DownLoad: Full-Size Img PowerPoint

图 4 鞍点模拟移动量ΔX_BEM, ΔY_BEM与目标移动量ΔX_obj, ΔY_obj间的误差情况　(a) 模型1的X_err分布; (b) 模型1的Y_err分布

Figure 4. Error between the simulated displacements of the saddle point (ΔX_BEM, ΔY_BEM) and the target displacements (ΔX_obj, ΔY_obj): (a) X_err distribution of model 1; (b) Y_err distribution of model 1.

DownLoad: Full-Size Img PowerPoint

图 5 鞍点模拟位移量(ΔX_BEM, ΔY_BEM)与目标移动量(ΔX_obj, ΔY_obj)间的误差情况　(a) 模型2的X_err分布; (b) 模型2的Y_err分布

Figure 5. Error between the simulated displacements of the saddle point (ΔX_BEM, ΔY_BEM) and the target displacements (ΔX_obj, ΔY_obj): (a) X_err distribution of model 2; (b) Y_err distribution of model 2.

DownLoad: Full-Size Img PowerPoint

图 6 鞍点模拟位移量(ΔX_BEM, ΔY_BEM)与目标移动量(ΔX_obj, ΔY_obj)间的误差情况　(a) 模型3的X_err分布; (b) 模型3的Y_err分布

Figure 6. Error between the simulated displacements of the saddle point (ΔX_BEM, ΔY_BEM) and the target displacements (ΔX_obj, ΔY_obj): (a) X_err distribution of model 3; (b) Y_err distribution of model 3.

DownLoad: Full-Size Img PowerPoint

DownLoad: Full-Size Img PowerPoint

表 1 初步拟合1的拟合情况

Table 1. The fitting situation of the preliminary fit 1.

E_XRF0(X, Y) E_XRF1(X, Y) E_XRF2(X, Y) E_YRF0(X, Y) E_YRF1(X, Y) E_YRF2(X, Y)

X阶数 1 2 2 1 2 2
Y阶数 3 3 3 1 3 3
Adj R-sq 0.9979 0.9977 0.9977 0.9992 0.9963 0.9963

DownLoad: CSV

表 2 拟合2的拟合情况

Table 2. The fitting situation of the fit 2.

E_XRF0(X, Y) E_XRF1(X, Y) E_XRF2(X, Y) E_YRF0(X, Y) E_YRF1(X, Y) E_YRF2(X, Y)

X阶数 1 2 2 1 2 2
Y阶数 4 4 4 1 4 4
Adj R-sq 0.9996 0.9997 0.9997 0.9992 0.9994 0.9994

DownLoad: CSV

表 3 拟合3的拟合情况

Table 3. The fitting situation of the fit 3.

E_XRF0(X, Y) E_XRF1(X, Y) E_XRF2(X, Y) E_YRF0(X, Y) E_YRF1(X, Y) E_YRF2(X, Y)

X阶数 5 5 5 5 5 5
Y阶数 5 5 5 5 5 5
Adj R-sq 1.0000 1.0000 1.0000 1.0000 0.9999 0.9999

DownLoad: CSV

map

[1]	Siverns J D, Quraishi Q 2017 Quantum Inf. Process. 16 314 Google Scholar
[2]	Ding X Y, Yu Q, Lu X Q, Wang X H, Huo X M, Qian X 2023 Anal. Chem. 95 2348 Google Scholar
[3]	Papanastasiou D, Kounadis D, Lekkas A, et al. 2022 J. Am. Soc. Mass Spectrom. 33 1990 Google Scholar
[4]	Ozawa A, Davila-Rodriguez J, Bounds J R, Schuessler H A, Hänsch T W, Udem T 2017 Nat. Commun. 8 44 Google Scholar
[5]	Amitrano V, Roggero A, Luchi P, Turro F, Vespucci L, Pederiva F 2023 Phys. Rev. D 107 023007 Google Scholar
[6]	Monroe C, Campbell W C, Duan L M, et al. 2021 Rev. Mod. Phys. 93 025001 Google Scholar
[7]	Niroula P, Shaydulin R, Yalovetzky R, Minssen P, Herman D, Hu S, Pistoia M 2022 Sci. Rep. 12 17171 Google Scholar
[8]	Pogorelov I, Feldker T, Marciniak C D, et al. 2021 PRX Quantum 2 020343 Google Scholar
[9]	Wang P P, Luan C Y, Qiao M, Um M, Zhang J H, Wang Y, Yuan X, Gu M L, Zhang J N, Kim K 2021 Nat. Commun. 12 233 Google Scholar
[10]	Manovitz T, Shapira Y, Gazit L, Akerman N, Ozeri R 2022 PRX Quantum 3 010347 Google Scholar
[11]	Mehta K K, Bruzewicz C D, McConnell R, Ram R J, Sage J M, Chiaverini J 2016 Nature Nanotech. 11 1066 Google Scholar
[12]	Ballance C J, Harty T P, Linke N M, Sepiol M A, Lucas D M 2016 Phys. Rev. Lett. 117 060504 Google Scholar
[13]	Rudolph M S, Toussaint N B, Katabarwa A, Johri S, Peropadre B, Perdomo-Ortiz A 2022 Phys. Rev. X 12 031010 Google Scholar
[14]	范桁 2018 67 120301 Google Scholar Fan H 2018 Acta Physica Sinica 67 120301 Google Scholar
[15]	Murali P, Debroy D M, Brown K R, Martonosi M 2022 Commun. ACM 65 101 Google Scholar
[16]	Pino J M, Dreiling J M, Figgatt C, Gaebler J P, Moses S A, Allman M, Baldwin C, Foss-Feig M, Hayes D, Mayer K 2021 Nature 592 209 Google Scholar
[17]	Ivory M, Setzer W J, Karl N, McGuinness H, DeRose C, Blain M, Stick D, Gehl M, Parazzoli L P 2021 Phys. Rev. X 11 041033 Google Scholar
[18]	Malinowski M, Allcock D T C, Ballance C J 2023 PRX Quantum 4 040313 Google Scholar
[19]	Romaszko Z D, Hong S, Siegele M, Puddy R K, Lebrun-Gallagher F R, Weidt S, Hensinger W K 2020 Nat. Rev. Phys. 2 285 Google Scholar
[20]	Wang Y H, Li Y, Yin Z Q, Zeng B 2018 npj Quantum Inf. 4 46 Google Scholar
[21]	Ryan-Anderson C, Bohnet J G, Lee K, et al. 2021 Phys. Rev. X 11 041058 Google Scholar
[22]	Mehta K K, Zhang C, Malinowski M, Nguyen T L, Stadler M, Home J P 2020 Nature 586 533 Google Scholar
[23]	Bao X Y, Cui J M, Fang D, Chen W B, Wang J, Huang Y F, Li C F, Guo G C 2023 JUSTC 53 0705 Google Scholar
[24]	Van Rynbach A, Maunz P, Kim J 2016 Appl. Phys. Lett. 109 221108 Google Scholar
[25]	Wang Z, Wang B R, Ma Q L, Guo J Y, Li M S, Wang Y, Rao X X, Huang Z Q, Luo L 2020 arXiv: 2004.08845 [quant-ph]
[26]	Holz P C, Auchter S, Stocker G, Valentini M, Lakhmanskiy K, Rössler C, Stampfer P, Sgouridis S, Aschauer E, Colombe Y, Blatt R 2020 Adv. Quantum Technol. 3 2000031 Google Scholar
[27]	Liu Y R, Wang Z, Xiang Z X, Wang Q K, Hu T Y, Wang X 2024 Chip 3 100078 Google Scholar
[28]	Hong S, Lee M, Cheon H, Kim T, Cho D I 2016 Sensors 16 616 Google Scholar
[29]	Read F H, Bowring N J 2011 Nucl. Instr. and Meth. A 645 273 Google Scholar
[30]	House M G 2008 Phys. Rev. A 78 033402 Google Scholar
[31]	Lauprêtre T, Achi B, Groult L, Carry É, Kersalé Y, Delehaye M, Hafiz M A, Lacroûte C 2023 Appl. Phys. B 129 37 Google Scholar
[32]	Zhang X, Ou B, Chen T, Xie Y, Wu W, Chen P 2020 Phys. Scr. 95 045103 Google Scholar
[33]	Zhang C, Mehta K K, Home J P 2022 New J. Phys. 24 073030 Google Scholar
[34]	王晨旭, 贺冉, 李睿睿, 陈炎, 房鼎, 崔金明, 黄运锋, 李传锋, 郭光灿 2022 71 133701 Google Scholar Wang C X, He R, Li R R, Chen Y, Fang D, Cui J M, Huang Y F, Li C F, Guo G C 2022 Acta Phys. Sin. 71 133701 Google Scholar
[35]	Kumph M, Holz P, Langer K, Meraner M, Niedermayr M, Brownnutt M, Blatt R 2016 New J. Phys. 18 023047 Google Scholar
[36]	Dehmelt H G 1968 Adv. At. Mol. Phys. 3 53 Google Scholar
[37]	Niedermayr M, Lakhmanskiy K, Kumph M, Partel S, Edlinger J, Brownnutt M, Blatt R 2014 New J. Phys. 16 113068 Google Scholar
[38]	吴宇恺, 段路明 2023 72 230302 Google Scholar Wu Y K, Duan L M 2023 Acta Phys. Sin. 72 230302 Google Scholar

[1]	Huang Ruo-Tong, Li Jiu-Sheng. Terahertz multibeam modulation reflection-coded metasurface. Acta Physica Sinica, 2023, 72(5): 054203. doi: 10.7498/aps.72.20221962
[2]	Liu Teng, Lu Peng-Fei, Hu Bi-Ying, Wu Hao, Lao Qi-Feng, Bian Ji, Liu Yang, Zhu Feng, Luo Le. Phonon-mediated many-body quantum entanglement and logic gates in ion traps. Acta Physica Sinica, 2022, 71(8): 080301. doi: 10.7498/aps.71.20220360
[3]	Zhang Jing-Yan, Dou Peng-Wei, Zhao Yun-Chi, Zhang Shi-Lei, Liu Jia-Qiang, Qi Jie, Lü Hao-Chang, Liu Ruo-Yang, Yu Guang-Hua, Jiang Yong, Shen Bao-Gen, Wang Shou-Guo. Multi-field manipulation in Hall balance. Acta Physica Sinica, 2021, 70(4): 048501. doi: 10.7498/aps.70.20201799
[4]	Guan Fu-Xin, Dong Shao-Hua, He Qiong, Xiao Shi-Yi, Sun Shu-Lin, Zhou Lei. Scatterings and wavefront manipulations of surface plasmon polaritons. Acta Physica Sinica, 2020, 69(15): 157804. doi: 10.7498/aps.69.20200614
[5]	Zhang Bao-Bao, Zhang Cheng-Yun, Zhang Zheng-Long, Zheng Hai-Rong. Surface plasmon mediated chemical reaction. Acta Physica Sinica, 2019, 68(14): 147102. doi: 10.7498/aps.68.20190345
[6]	Zhou Qiang, Lin Shu-Pei, Zhang Pu, Chen Xue-Wen. Quasinormal mode analysis of extremely localized optical field in body-of-revolution plasmonic structures. Acta Physica Sinica, 2019, 68(14): 147104. doi: 10.7498/aps.68.20190434
[7]	Zhang Shu-He, Liang Zhen, Zhou Jin-Hua. Using quaternions to analyze the trapping force of an ellipsoidal bead. Acta Physica Sinica, 2017, 66(4): 048701. doi: 10.7498/aps.66.048701
[8]	Hu Yang, Wang Qiu-Liang, Li Yi, Zhu Xu-Chen, Niu Chao-Qun. Optimization of magnetic resonance imaging high-order axial shim coils using boundary element method. Acta Physica Sinica, 2016, 65(21): 218301. doi: 10.7498/aps.65.218301
[9]	Huang Fei-Hu, Peng Jian, You Ming-Yang. Analyses of characetristics of air passenger group mobility behaviors. Acta Physica Sinica, 2016, 65(22): 228901. doi: 10.7498/aps.65.228901
[10]	Jiao Yun-Long, Liu Xiao-Jun, Pang Ming-Hua, Liu Kun. Analyses of droplet spreading and the movement of wetting line on a solid surface. Acta Physica Sinica, 2016, 65(1): 016801. doi: 10.7498/aps.65.016801
[11]	Yin Ji-Fu, You Yun-Xiang, Li Wei, Hu Tian-Qun. Numerical analysis for the characteristics of flow control around a circular cylinder with a turbulent boundary layer separation using the electromagnetic force. Acta Physica Sinica, 2014, 63(4): 044701. doi: 10.7498/aps.63.044701
[12]	Zhang Jian, Chen Shu-Ming, Liu Wei. Substrate effect on surface-electrode ion trap and hybrid design for ion trap. Acta Physica Sinica, 2014, 63(6): 060303. doi: 10.7498/aps.63.060303
[13]	Yang Li-Xia, Ma Hui, Shi Wei-Dong, Shi Li-Juan, Yu Ping-Ping. Finite difference time domain analysis on electromagnetic scattering characteristic of plasma thin layer based on surface impedance boundary condition method. Acta Physica Sinica, 2013, 62(3): 034102. doi: 10.7498/aps.62.034102
[14]	Xu Zan-Xin, Wang Yue, Si Hong-Bo, Feng Zhen-Ming. Analysis of urban human mobility behavior based on random matrix theory. Acta Physica Sinica, 2011, 60(4): 040501. doi: 10.7498/aps.60.040501
[15]	Su Dong, Tang Chang-Jian, Liu Pu-Kun. Boundary effect analysis of electromagnetic mode in the beam-ion channel. Acta Physica Sinica, 2007, 56(5): 2802-2807. doi: 10.7498/aps.56.2802
[16]	You Tian-Xue, Yuan Bao-Shan, Li Fang-Zhu. Plasma boundary identification in HL-2A by means of the movable current filaments method. Acta Physica Sinica, 2007, 56(9): 5323-5329. doi: 10.7498/aps.56.5323
[17]	Miao Jiang-Ping, Wu Zong-Han, Sun Cheng-Xiu, Sun Yue-Ming. The self-consistent theoretical study of the effect of surface plasmon and polariton on electronic transport Ⅱ——The calculation and analysis of molecular orbital field in MIM system. Acta Physica Sinica, 2005, 54(5): 2282-2290. doi: 10.7498/aps.54.2282
[18]	LIU HONG-XIANG, WEI HE-LIN, LIU ZU-LI, LIU YAN-HONG, WANG JUN-ZHEN. EFFECT OF THE MAGNETIC MIRROR FIELD ON THE ION ENERGY DISTRIBUTIONS IN A RADIO F REQUENCY PLASMA. Acta Physica Sinica, 2000, 49(9): 1764-1768. doi: 10.7498/aps.49.1764
[19]	GAO KE-LIN, YAN MIN, LUO XUE-LI, ZHU XI-WEN, HUANG GUI-LONG, LI JIAO-MEI, SHI LEI. . Acta Physica Sinica, 1995, 44(1): 43-49. doi: 10.7498/aps.44.43
[20]	ZHU YEI-ZHUNG, LEE TSE-CHING. ANGULAR DISTRIBUTION OF THE FISSION FRAGMENTS AND THE STRUCTURE AT THE SADDLE POINT. Acta Physica Sinica, 1964, 20(10): 1003-1018. doi: 10.7498/aps.20.1003

Catalog

Vol. 74, Issue 4 - 2025-02-20

Metrics

Abstract views: 501
PDF Downloads: 14
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板