-
置信传播(BP)算法作为推断概率图模型的主流算法是求解随机块模型中联合概率分布的重要方法之一. 但现有的方法要么在处理核边结构问题上存在精度不足问题, 要么在理论的推导上存在近似太多, 导致求解过程复杂且难以理解问题, 或两个问题均存在. 当然, 精度不足也是由近似多造成的. 导致理论近似多且推导复杂的主要原因, 是随机块模型推断过程中求解联合概率分布并不是直接套用BP算法, 即处理的图(网络)与概率图模型的图不统一. 因此, 本文利用平均场近似修正联合概率分布, 使其完全匹配BP算法的迭代公式, 这样使得在理论推导上简单易懂. 最后通过实验验证, 该方法是有效的.As a mainstream algorithm for inferring probabilistic graphical models, belief propagation (BP) algorithm is one of the most important methods to solve the joint probability distribution in the stochastic block model. However, existing methods either lead to low accuracy in dealing with the core-periphery structure problem, or the theoretical derivation is difficult to understand due to a large number of approximation, or both exist. Of course, the reason for low accuracy comes from too many approximations. The main reason for many approximations and complex theoretical derivation is that the joint probability distribution in the inference process of the stochastic block model is not directly solved by the BP algorithm, that is, the graph (network) being processed is not consistent with the graph considered in the probabilistic graph model. Therefore, in this paper, a mean-field approximation is developed to modify the joint probability distribution to make the BP algorithm match perfectly, which makes the theoretical derivation easy to understand. Finally, the effectiveness of the proposed method is validated by the experimental results.
-
Keywords:
- stochastic block model /
- belief propagation algorithm /
- joint probability distribution /
- mean-field approximation
[1] 张海峰, 王文旭 2020 69 088906
Google Scholar
Zhang H F, Wang W X 2020 Acta Phys. Sin. 69 088906
Google Scholar
[2] Guimerà R, Mossa S, Turtschi A, Amaral L A N 2005 PNAS 102 7794
Google Scholar
[3] Newman M E J 2006 Phys. Rev. E 74 36104
Google Scholar
[4] Benson A R, Gleich D F, Leskovec J 2016 Science 353 163
Google Scholar
[5] Xiang B B, Bao Z K, Ma C, Zhang X, Chen H S, Zhang H F 2018 Chaos 28 13122
Google Scholar
[6] Newman M E J 2003 SIAM Rev. 45 167
Google Scholar
[7] Leicht E A, Newman M E J 2008 Phys. Rev. Lett. 100 118703
Google Scholar
[8] Newman M E J 2006 Proc. Natl Acad. Sci. U.S.A. 103 8577
Google Scholar
[9] Newman M E J 2012 Nat. Phys. 8 25
Google Scholar
[10] Zhang X, Newman M E J 2015 Phys. Rev. E 92 52808
Google Scholar
[11] Lee D D, Seung H S 1999 Nature 401 788
Google Scholar
[12] 常振超, 陈鸿昶, 刘阳, 于洪涛, 黄瑞阳 2015 64 218901
Google Scholar
Chang Z C, Chen H C, Liu Y, Yu H T, Huang R Y 2015 Acta Phys. Sin. 64 218901
Google Scholar
[13] Shao J, Han Z, Yang Q, Zhou T 2015 Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining Sydney NSW, Australia, August 10–13, 2015 p1075
[14] Gregory S 2010 New J. Phys. 12 103018
Google Scholar
[15] Karrer B, Newman M E J 2011 Phys. Rev. E 83 16107
Google Scholar
[16] Decelle A, Krzakala F, Moore C, ZdeborováL 2011 Phys. Rev. Lett. 107 65701
Google Scholar
[17] Ledwith M 2020 Community development: A critical approach (Bristol: Policy Press) pp1–252
[18] 王兴元, 赵仲祥 2014 63 178901
Google Scholar
Wang X Y, Zhao Z X 2014 Acta Phys. Sin. 63 178901
Google Scholar
[19] Everett M G, Borgatti S P 2000 Social Networks 21 397
Google Scholar
[20] Verma T, Russmann F, Araújo N A M, Nagler J, Herrmann H J 2016 Nat. Commun. 7 10441
Google Scholar
[21] Lee S H, Cucuringu M, Porter M A 2014 Phys. Rev. E 89 32810
Google Scholar
[22] Rombach P, Porter M A, Fowler J H, Mucha P J 2017 SIAM Rev. 59 619
Google Scholar
[23] Kojaku S, Masuda N 2017 Phys. Rev. E 96 52313
Google Scholar
[24] Kojaku S, Masuda N 2018 New J. Phys. 20 43012
Google Scholar
[25] Ma C, Xiang B B, Chen H S, Zhang H F 2020 Chaos 30 23112
Google Scholar
[26] Zhang X, Martin T, Newman M E J 2015 Phys. Rev. E 91 32803
Google Scholar
[27] Della Rossa F, Dercole F, Piccardi C 2013 Sci. Rep. 3 1467
Google Scholar
[28] Ma C, Xiang B B, Chen H S, Small M, Zhang H F 2018 Chaos 28 53121
Google Scholar
[29] 康玲, 项冰冰, 翟素兰, 鲍中奎, 张海峰 2018 67 198901
Google Scholar
Kang L, Xiang B B, Zhai S L, Bao Z K, Zhang H F 2018 Acta Phys. Sin. 67 198901
Google Scholar
[30] Ball B, Karrer B, Newman M E J 2011 Phys. Rev. E 84 36103
Google Scholar
[31] Decelle A, Krzakala F, Moore C, ZdeborováL 2011 Phys. Rev. E 84 66106
Google Scholar
[32] Mugisha S, Zhou H J 2016 Phys. Rev. E 94 12305
Google Scholar
[33] Yedidia J S, Freeman W T, Weiss Y 2005 IEEE Trans. Inf. Theory 51 2282
Google Scholar
[34] Mezard M, Montanari A 2009 Information, Physics, and Computation (Oxford: Oxford University Press) pp304–305
[35] Perotti J I, Tessone C J, Clauset A, Caldarelli G 2018 arXiv: 1806.07005 v1[soc-ph]
[36] Dempster A P, Laird N M, Rubin D B 1977 Journal of the Royal Statistical Society: Series B (Methodological) 39 1
Google Scholar
[37] Tiago P, Peixoto 2019 Advances in Network Clustering and Blockmodeling (New York:Wiley) pp289–332
[38] Zhang P, Moore C 2014 Proc. Natl. Acad. Sci. U.S.A. 111 18144
Google Scholar
[39] Gerlof B 2009 Proceedings of the 21th Biennial GSCL Conference Potsdam, Germany, September 30–October 2 2009 p31
[40] Sokolova M, Laxpalme G 2009 Inf. Process. Manage. 45 427
Google Scholar
-
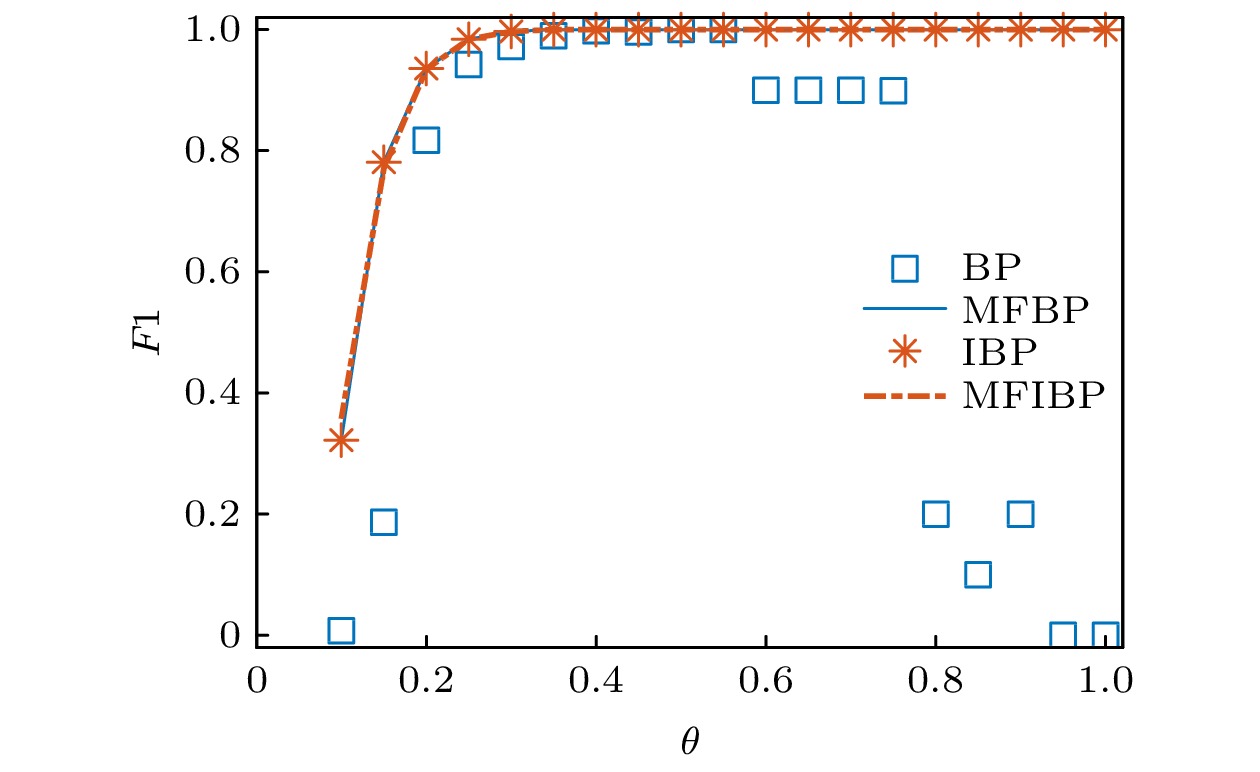
图 1 稀疏基准网络社团结构探测 (a)
$n = 10000$ ,$c = 3$ ,$\gamma = {[0.5,\; 0.5]^{\rm T}}$ ,$\varepsilon^* = 0.27$ ; (b)$n = 200$ ,$c = 10$ ,$\gamma = {[0.5,\; 0.5]^{\rm T}}$ ,$\varepsilon^* = 0.520$ ; (c)$n = 200$ ,$c = 10$ ,$\gamma = {[0.3,\; 0.7]^{\rm T}}$ ; (d)$n = 200$ ,$c = 10$ ,$\gamma = {[1/3,\; 1/3,\; 1/3]^{\rm T}}$ ,$\varepsilon^* = 0.419$ Fig. 1. Community structure detection in sparse benchmark networks: (a)
$n = 10000$ ,$c = 3$ ,$\gamma = {[0.5,\; 0.5]^{\rm T}}$ ,$\varepsilon^* = 0.27$ ; (b)$n = 200$ ,$c = 10$ ,$\gamma = {[0.5,\; 0.5]^{\rm T}}$ ,$\varepsilon^* = 0.520$ ; (c)$n = 200$ ,$c = 10$ ,$\gamma = {[0.3,\; 0.7]^{\rm T}}$ ; (d)$n = 200$ ,$c = 10$ ,$\gamma = {[1/3,\; 1/3, \;1/3]^{\rm T}},$ $\varepsilon^* = 0.419$ 
图 2 稠密基准网络社团结构探测 (a)
$n = 200$ ,$c = 50$ ,$\gamma = {[0.5,\; 0.5]^{\rm T}}$ ,$\varepsilon^* = 0.75$ ; (b)$n = 200$ ,$c = 50$ ,$\gamma = {[0.3, \;0.7]^{\rm T}}$ , (c)$n = 200$ ,$c = 30$ ,$\gamma = {[1/3,\; 1/3,\; 1/3]^{\rm T}}$ ,$\varepsilon^* = 0.599$ Fig. 2. Community structure detection in dense benchmark networks: (a)
$n = 200$ ,$c = 50$ ,$\gamma = {[0.5,\; 0.5]^{\rm T}}$ ,$\varepsilon^* = 0.75$ ; (b)$n = 200$ ,$c = 50$ ,$\gamma = {[0.3,\; 0.7]^{\rm T}}$ ; (c)$n = 200$ ,$c = 30$ ,$\gamma = {[1/3,\; 1/3,\; 1/3]^{\rm T}}$ ,$\varepsilon^* = 0.599$ -
[1] 张海峰, 王文旭 2020 69 088906
Google Scholar
Zhang H F, Wang W X 2020 Acta Phys. Sin. 69 088906
Google Scholar
[2] Guimerà R, Mossa S, Turtschi A, Amaral L A N 2005 PNAS 102 7794
Google Scholar
[3] Newman M E J 2006 Phys. Rev. E 74 36104
Google Scholar
[4] Benson A R, Gleich D F, Leskovec J 2016 Science 353 163
Google Scholar
[5] Xiang B B, Bao Z K, Ma C, Zhang X, Chen H S, Zhang H F 2018 Chaos 28 13122
Google Scholar
[6] Newman M E J 2003 SIAM Rev. 45 167
Google Scholar
[7] Leicht E A, Newman M E J 2008 Phys. Rev. Lett. 100 118703
Google Scholar
[8] Newman M E J 2006 Proc. Natl Acad. Sci. U.S.A. 103 8577
Google Scholar
[9] Newman M E J 2012 Nat. Phys. 8 25
Google Scholar
[10] Zhang X, Newman M E J 2015 Phys. Rev. E 92 52808
Google Scholar
[11] Lee D D, Seung H S 1999 Nature 401 788
Google Scholar
[12] 常振超, 陈鸿昶, 刘阳, 于洪涛, 黄瑞阳 2015 64 218901
Google Scholar
Chang Z C, Chen H C, Liu Y, Yu H T, Huang R Y 2015 Acta Phys. Sin. 64 218901
Google Scholar
[13] Shao J, Han Z, Yang Q, Zhou T 2015 Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining Sydney NSW, Australia, August 10–13, 2015 p1075
[14] Gregory S 2010 New J. Phys. 12 103018
Google Scholar
[15] Karrer B, Newman M E J 2011 Phys. Rev. E 83 16107
Google Scholar
[16] Decelle A, Krzakala F, Moore C, ZdeborováL 2011 Phys. Rev. Lett. 107 65701
Google Scholar
[17] Ledwith M 2020 Community development: A critical approach (Bristol: Policy Press) pp1–252
[18] 王兴元, 赵仲祥 2014 63 178901
Google Scholar
Wang X Y, Zhao Z X 2014 Acta Phys. Sin. 63 178901
Google Scholar
[19] Everett M G, Borgatti S P 2000 Social Networks 21 397
Google Scholar
[20] Verma T, Russmann F, Araújo N A M, Nagler J, Herrmann H J 2016 Nat. Commun. 7 10441
Google Scholar
[21] Lee S H, Cucuringu M, Porter M A 2014 Phys. Rev. E 89 32810
Google Scholar
[22] Rombach P, Porter M A, Fowler J H, Mucha P J 2017 SIAM Rev. 59 619
Google Scholar
[23] Kojaku S, Masuda N 2017 Phys. Rev. E 96 52313
Google Scholar
[24] Kojaku S, Masuda N 2018 New J. Phys. 20 43012
Google Scholar
[25] Ma C, Xiang B B, Chen H S, Zhang H F 2020 Chaos 30 23112
Google Scholar
[26] Zhang X, Martin T, Newman M E J 2015 Phys. Rev. E 91 32803
Google Scholar
[27] Della Rossa F, Dercole F, Piccardi C 2013 Sci. Rep. 3 1467
Google Scholar
[28] Ma C, Xiang B B, Chen H S, Small M, Zhang H F 2018 Chaos 28 53121
Google Scholar
[29] 康玲, 项冰冰, 翟素兰, 鲍中奎, 张海峰 2018 67 198901
Google Scholar
Kang L, Xiang B B, Zhai S L, Bao Z K, Zhang H F 2018 Acta Phys. Sin. 67 198901
Google Scholar
[30] Ball B, Karrer B, Newman M E J 2011 Phys. Rev. E 84 36103
Google Scholar
[31] Decelle A, Krzakala F, Moore C, ZdeborováL 2011 Phys. Rev. E 84 66106
Google Scholar
[32] Mugisha S, Zhou H J 2016 Phys. Rev. E 94 12305
Google Scholar
[33] Yedidia J S, Freeman W T, Weiss Y 2005 IEEE Trans. Inf. Theory 51 2282
Google Scholar
[34] Mezard M, Montanari A 2009 Information, Physics, and Computation (Oxford: Oxford University Press) pp304–305
[35] Perotti J I, Tessone C J, Clauset A, Caldarelli G 2018 arXiv: 1806.07005 v1[soc-ph]
[36] Dempster A P, Laird N M, Rubin D B 1977 Journal of the Royal Statistical Society: Series B (Methodological) 39 1
Google Scholar
[37] Tiago P, Peixoto 2019 Advances in Network Clustering and Blockmodeling (New York:Wiley) pp289–332
[38] Zhang P, Moore C 2014 Proc. Natl. Acad. Sci. U.S.A. 111 18144
Google Scholar
[39] Gerlof B 2009 Proceedings of the 21th Biennial GSCL Conference Potsdam, Germany, September 30–October 2 2009 p31
[40] Sokolova M, Laxpalme G 2009 Inf. Process. Manage. 45 427
Google Scholar
下载:
计量
- 文章访问数: 4421
- PDF下载量: 65
- 被引次数: 0
