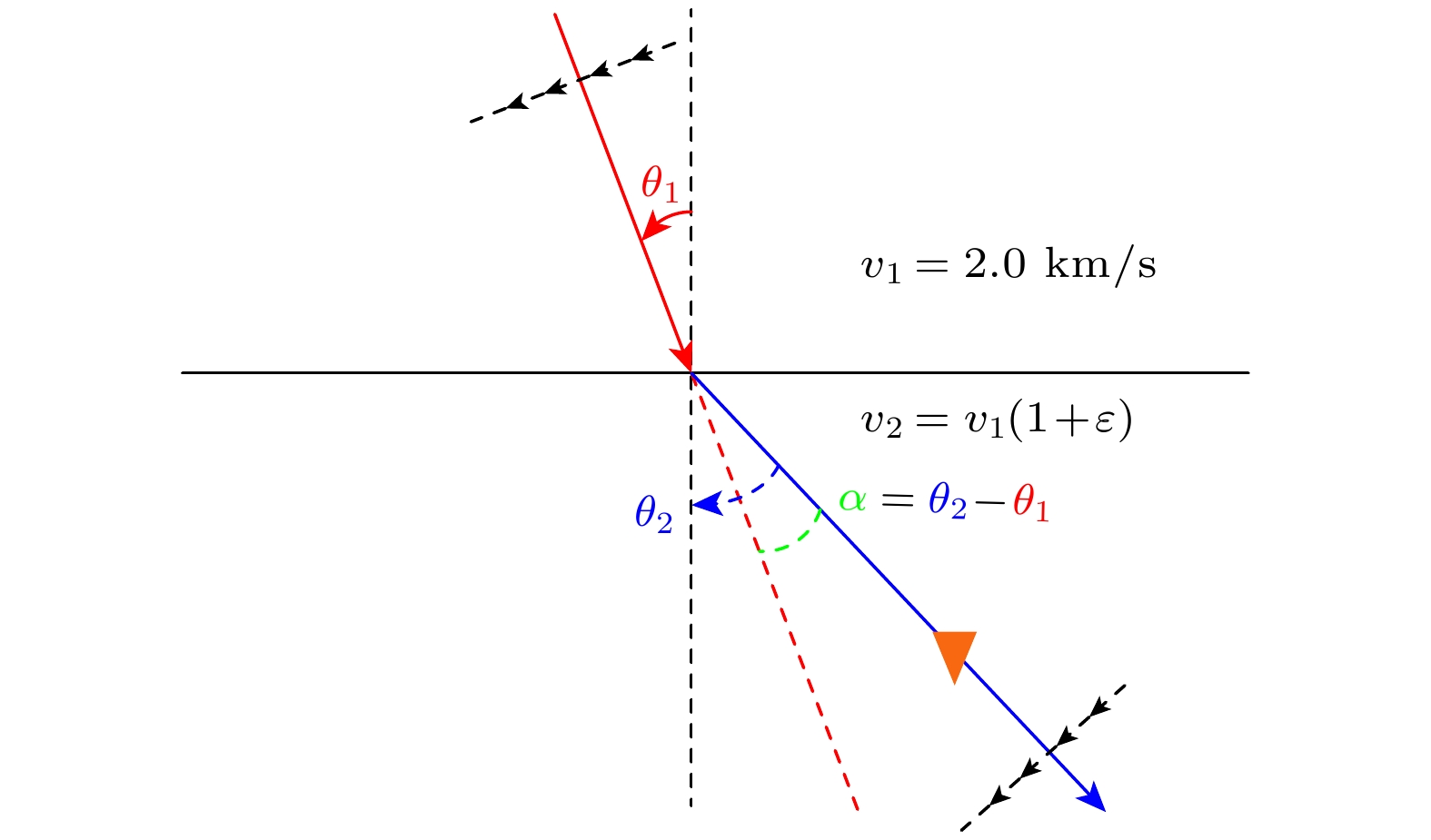
-
传统的波动方程线性化近似理论, 如一阶Born近似或Rytov近似等, 均隐含“弱散射”假设, 因此仅适用于弱扰动模型. 为克服“弱散射”假设的制约并将波动方程线性化近似理论推广至强扰动模型中, 提出了适用于预测前向散射波相位扰动的保相位理论. 通过将标量声波方程Rytov变换得到的非线性Ricatti方程中关于未知解(即散射场复相位)的积分, 在Wentzel-Kramers-Brillouin-Jeffreys (WKBJ)近似下转化为对散射角和模型扰动的积分, 给出了前向散射场相位扰动的显式积分表达. 理论推导表明: 对于一维波传播问题, 保相位理论可以精确预测任意速度扰动模型中前向散射波的相位扰动. 对于小角度前向散射, 保相位理论可以进行线性化近似, 得到广义Rytov近似. 数值实验表明, 对于高维问题, 相比于一阶Rytov近似, 广义Rytov近似可以更好地预测前向小角度散射场的相位扰动, 且适用于强速度扰动模型. 广义Rytov近似拓展了Rytov近似的成立条件和适用范围, 可以直接应用于地震层析成像及医学超声透射成像中, 从而降低层析反问题对初始模型的依赖性并加速反演收敛.The conventional wave-equation linearization methods, such as the first-order Born or Rytov approximation, always implicitly imply a weak-scattering assumption, making it valid only for weak perturbation models. To extend the wave-equation linearization theory to strong perturbation models, we consider a scenario that the reference model is smooth within the scale of the incident wave length, and propose a phase-preserving method which can predict the phase perturbation of forward scattering wave field. First, we introduce the WKBJ approximation to the scattered- and incident wave fields so that the integral of the unknown solution (i.e. the scattered field) in the nonlinear Ricatti integral equation can be replaced by the integral of scattering-angle and model perturbation, yielding an explicit expression of the scattered field. Theoretical derivation shows that the proposed phase-preserving method can accurately predict the phase-perturbation of forward scattered wave field regardless of the strength of velocity perturbations for one-dimensional wave propagation problem. To apply the phase-preserving approximation to the inverse problem, we further consider a scenario of small-angle forward propagation. In this case, the phase-preserving approximation can be linearized by neglecting the influence of scattering angles, leading to a linear relation between the scattered field and the model perturbation, which we refer to as the generalized Rytov approximation. Numerical experiments demonstrate that the generalized Rytov approximation can predict the phase perturbation of the scattered field with higher accuracy for small-angle forward propagation, and is suitable for strong model perturbations. The generalized Rytov approximation extends the validity and the scope of application of the traditional Rytov approximation. In specific application fields such as the seismic traveltime tomography or medical ultrasonic transmission imaging, a new traveltime/phase sensitivity kernel can be derived by replacing the conventional Rytov approximation with the proposed method, which can increase the inversion accuracy and speed up the convergence.
-
Keywords:
- wave-equation linearization /
- phase-preserving approximation /
- forward scattering /
- strong perturbation model
[1] Aki K 1973 J. Geophys. Res. 78 1334
 Google Scholar
Google Scholar
[2] Born M 1926 Z. Phys. 38 803
 Google Scholar
Google Scholar
[3] Newton R G 1961 R. Oehme, Phys. Rev 70 121
[4] Newton R G 1989 Inverse Schrödinger Scattering in Three Dimensions (New York: Springer-Verlag) pp25, 26
[5] Päivärinta L, Erkki S 1991 SIAM J. Math. Anal. 22 480
 Google Scholar
Google Scholar
[6] Wu R S, Zheng Y 2014 Geophys. J. Int. 196 1827
 Google Scholar
Google Scholar
[7] Wu R S, Wang B, Hu C 2015 Inverse Probl. 31 115004
 Google Scholar
Google Scholar
[8] 王本锋, 吴如山, 陈小宏, 陆文凯 2016 地球 59 2257
 Google Scholar
Google Scholar
Wang B F, Wu R S, Chen X H, Lu W K 2016 Chin. J. Geophys. 59 2257
 Google Scholar
Google Scholar
[9] Rytov S M 1937 Izv. Akad. Nauk. SSSR Ser Fiz 2 223 (in Russia)
[10] Chernov L A, Silverman R A, Morse P M 1960 Phys. Today 13 50
 Google Scholar
Google Scholar
[11] Tartarski V L 1971 Jerusalem: Israel Program for Scientific Translations (London: Oldbourne Press) pp218–220
[12] Ishimaru A 1978 Wave Propagation and Scattering in Random Media (Vol. II) (New York: Academic Press) pp376–378
[13] Devaney A J 1984 IEEE T. Geosci. Remote 22 3
 Google Scholar
Google Scholar
[14] Wu R S, Toksöz M N 1987 Geophysics 52 11
 Google Scholar
Google Scholar
[15] Tsihrintzis G A, Devaney A J 2000 IEEE T. Image Process. 9 1560
 Google Scholar
Google Scholar
[16] Wu R S, Flatté S M 1990 Pure Appl. Geophys. 132 175
 Google Scholar
Google Scholar
[17] Montelli R, Nolet G, Dahlen F A, Masters G, Engdahl E R, Hung S H 2004 Science 303 338
 Google Scholar
Google Scholar
[18] Zhou Y, Nolet G, Dahlen F A, Laske G 2006 Geophys. Res. 111 B04304
 Google Scholar
Google Scholar
[19] 刘玉柱, 董良国, 李培明, 王毓炜, 朱金平, 马在田 2009 地球 52 2310
 Google Scholar
Google Scholar
Liu Y Z, Dong L G, Li P M, Wang Y W, Zhu J P, Ma Z T 2009 Chin. J. Geophys. 52 2310
 Google Scholar
Google Scholar
[20] Xu W, Xie X B, Geng J 2015 Pure Appl. Geophys. 172 1409
 Google Scholar
Google Scholar
[21] 冯波, 罗飞, 王华忠 2019 地球 62 2217
 Google Scholar
Google Scholar
Feng B, Luo F, Wang H Z 2019 Chin. J. Geophys. 62 2217
 Google Scholar
Google Scholar
[22] Wu R S 2003 Pure Appl. Geophys. 160 509
 Google Scholar
Google Scholar
[23] Tsihrintzis G A, Devaney A J 2000 IEEE T. Inform. Theory 46 1748
 Google Scholar
Google Scholar
[24] Manning R M 1996 Radiophys. Quant. El. 39 287
 Google Scholar
Google Scholar
[25] Kim B C, Tinin M V 2009 Waves Random Complex 19 284
 Google Scholar
Google Scholar
[26] 汪燚林, 董良国 2021 地球 64 3701
 Google Scholar
Google Scholar
Wang Y L, Dong L G 2021 Chin. J. Geophys. 64 3701
 Google Scholar
Google Scholar
[27] Clayton R W, Stolt R H 1981 Geophysics 46 1559
 Google Scholar
Google Scholar
[28] Flatté S M 1979 Sound Transmission Through a Fluctuating Ocean (London: Cambridge University Press) p165
[29] Snieder R, Lomax A 1996 Geophys. J. Int. 125 796
 Google Scholar
Google Scholar
[30] 郭敦仁 1991 数学物理方法(第二版) (北京: 高等教育出版社) 第361页
Guo D R 1991 Methods of Mathematical Physics (2nd Ed.) (Beijing: Higher Education Press ) p361
[31] 钟万勰, 高强 2005 计算力学学报 22 1
Zhong W X, Gao Q 2005 Chin. J. Comput. Mech. 22 1
-
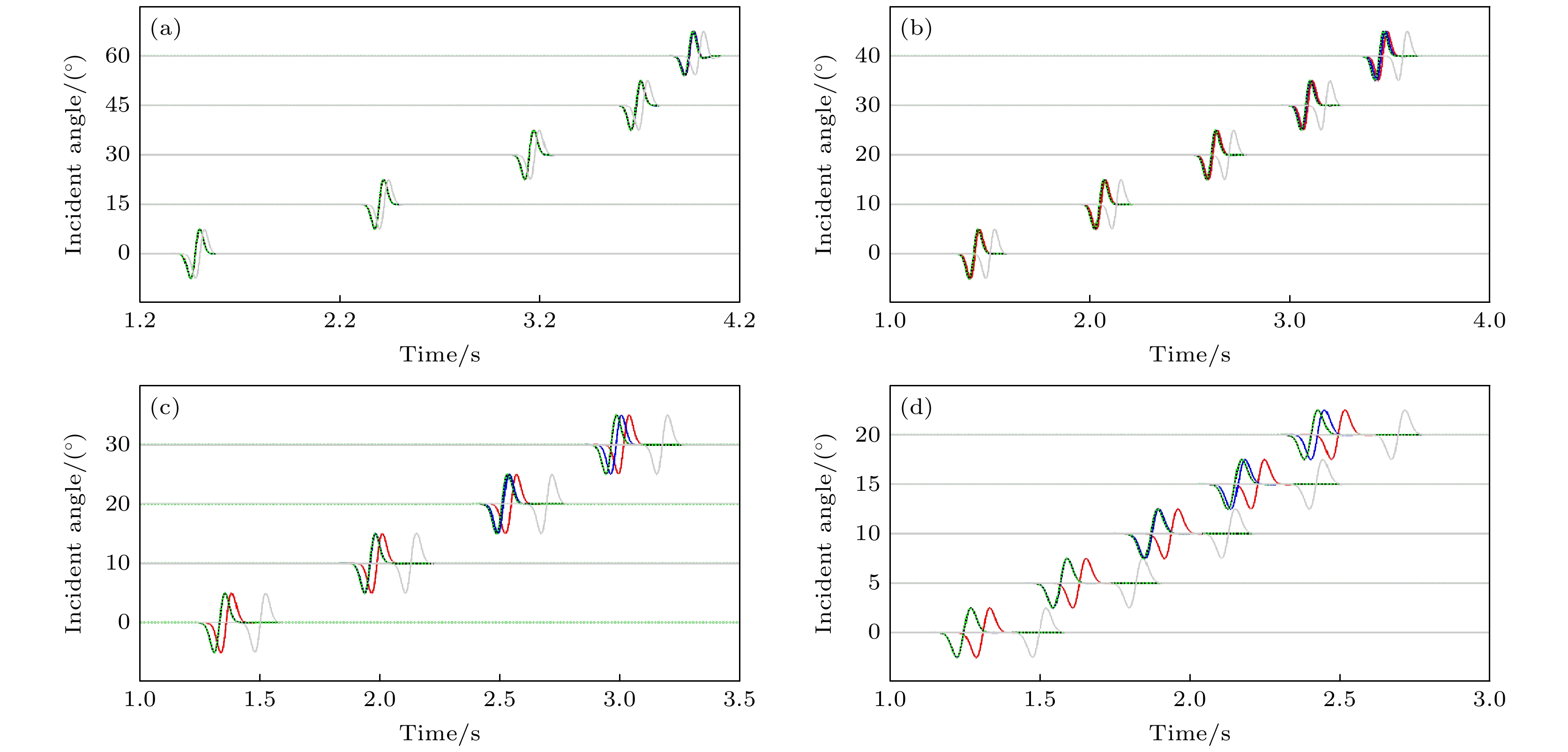
图 3 双层速度模型中地震记录的(振幅归一化)波形对比. (a)—(d)分别代表速度扰动百分比为5%, 20%, 50%和100%. 黑色和灰色曲线分别为真实模型及背景模型(第1层速度)中正演的地震记录, 红色和蓝色曲线分别为一阶Rytov近似和广义Rytov近似得到的地震记录, 绿色虚线为保相位近似解(保留散射角)
Fig. 3. Seismic waveforms calculated using the two-layered model. Panel (a)–(d) stand for velocity models with the velocity percentages of 5%, 20%, 50% and 100%, respectively. The black- and gray-curve are the waveforms in true and background model, respectively; the red- and blue-curve are the first-order and the GRA results, respectively, the green-dotted curve is the phase-preserving solution (keeping the scattering-angle).
-
[1] Aki K 1973 J. Geophys. Res. 78 1334
 Google Scholar
Google Scholar
[2] Born M 1926 Z. Phys. 38 803
 Google Scholar
Google Scholar
[3] Newton R G 1961 R. Oehme, Phys. Rev 70 121
[4] Newton R G 1989 Inverse Schrödinger Scattering in Three Dimensions (New York: Springer-Verlag) pp25, 26
[5] Päivärinta L, Erkki S 1991 SIAM J. Math. Anal. 22 480
 Google Scholar
Google Scholar
[6] Wu R S, Zheng Y 2014 Geophys. J. Int. 196 1827
 Google Scholar
Google Scholar
[7] Wu R S, Wang B, Hu C 2015 Inverse Probl. 31 115004
 Google Scholar
Google Scholar
[8] 王本锋, 吴如山, 陈小宏, 陆文凯 2016 地球 59 2257
 Google Scholar
Google Scholar
Wang B F, Wu R S, Chen X H, Lu W K 2016 Chin. J. Geophys. 59 2257
 Google Scholar
Google Scholar
[9] Rytov S M 1937 Izv. Akad. Nauk. SSSR Ser Fiz 2 223 (in Russia)
[10] Chernov L A, Silverman R A, Morse P M 1960 Phys. Today 13 50
 Google Scholar
Google Scholar
[11] Tartarski V L 1971 Jerusalem: Israel Program for Scientific Translations (London: Oldbourne Press) pp218–220
[12] Ishimaru A 1978 Wave Propagation and Scattering in Random Media (Vol. II) (New York: Academic Press) pp376–378
[13] Devaney A J 1984 IEEE T. Geosci. Remote 22 3
 Google Scholar
Google Scholar
[14] Wu R S, Toksöz M N 1987 Geophysics 52 11
 Google Scholar
Google Scholar
[15] Tsihrintzis G A, Devaney A J 2000 IEEE T. Image Process. 9 1560
 Google Scholar
Google Scholar
[16] Wu R S, Flatté S M 1990 Pure Appl. Geophys. 132 175
 Google Scholar
Google Scholar
[17] Montelli R, Nolet G, Dahlen F A, Masters G, Engdahl E R, Hung S H 2004 Science 303 338
 Google Scholar
Google Scholar
[18] Zhou Y, Nolet G, Dahlen F A, Laske G 2006 Geophys. Res. 111 B04304
 Google Scholar
Google Scholar
[19] 刘玉柱, 董良国, 李培明, 王毓炜, 朱金平, 马在田 2009 地球 52 2310
 Google Scholar
Google Scholar
Liu Y Z, Dong L G, Li P M, Wang Y W, Zhu J P, Ma Z T 2009 Chin. J. Geophys. 52 2310
 Google Scholar
Google Scholar
[20] Xu W, Xie X B, Geng J 2015 Pure Appl. Geophys. 172 1409
 Google Scholar
Google Scholar
[21] 冯波, 罗飞, 王华忠 2019 地球 62 2217
 Google Scholar
Google Scholar
Feng B, Luo F, Wang H Z 2019 Chin. J. Geophys. 62 2217
 Google Scholar
Google Scholar
[22] Wu R S 2003 Pure Appl. Geophys. 160 509
 Google Scholar
Google Scholar
[23] Tsihrintzis G A, Devaney A J 2000 IEEE T. Inform. Theory 46 1748
 Google Scholar
Google Scholar
[24] Manning R M 1996 Radiophys. Quant. El. 39 287
 Google Scholar
Google Scholar
[25] Kim B C, Tinin M V 2009 Waves Random Complex 19 284
 Google Scholar
Google Scholar
[26] 汪燚林, 董良国 2021 地球 64 3701
 Google Scholar
Google Scholar
Wang Y L, Dong L G 2021 Chin. J. Geophys. 64 3701
 Google Scholar
Google Scholar
[27] Clayton R W, Stolt R H 1981 Geophysics 46 1559
 Google Scholar
Google Scholar
[28] Flatté S M 1979 Sound Transmission Through a Fluctuating Ocean (London: Cambridge University Press) p165
[29] Snieder R, Lomax A 1996 Geophys. J. Int. 125 796
 Google Scholar
Google Scholar
[30] 郭敦仁 1991 数学物理方法(第二版) (北京: 高等教育出版社) 第361页
Guo D R 1991 Methods of Mathematical Physics (2nd Ed.) (Beijing: Higher Education Press ) p361
[31] 钟万勰, 高强 2005 计算力学学报 22 1
Zhong W X, Gao Q 2005 Chin. J. Comput. Mech. 22 1
计量
- 文章访问数: 4802
- PDF下载量: 67
- 被引次数: 0













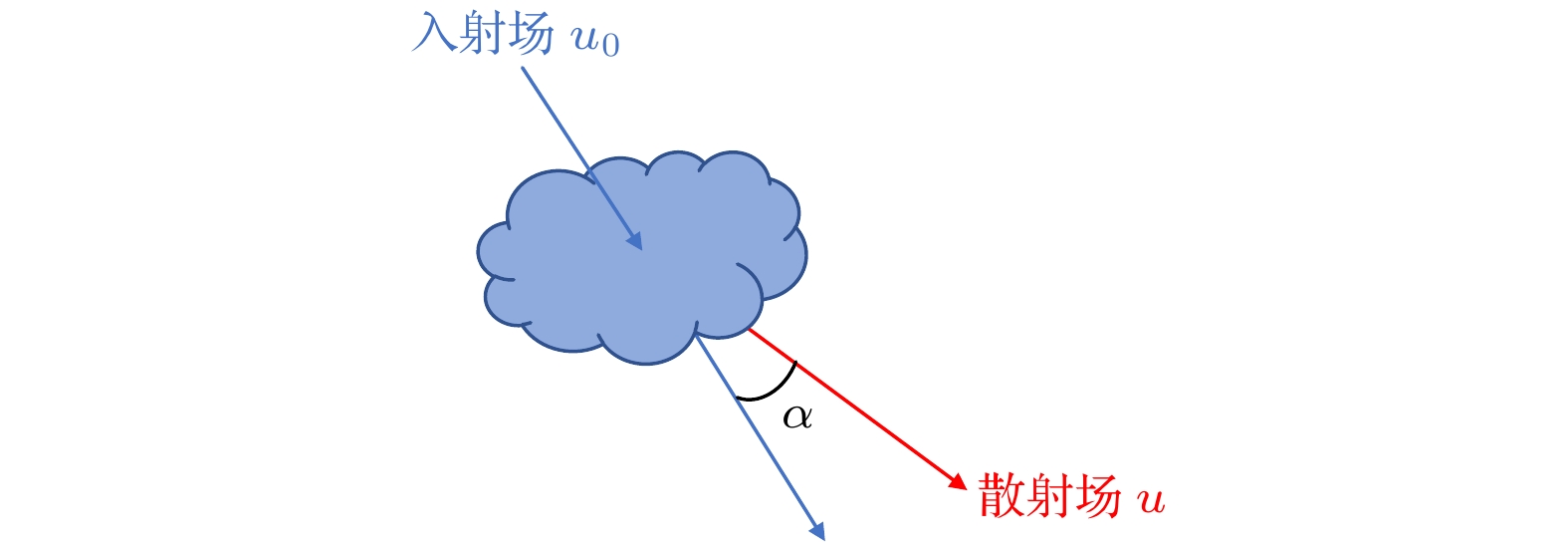
 下载:
下载: