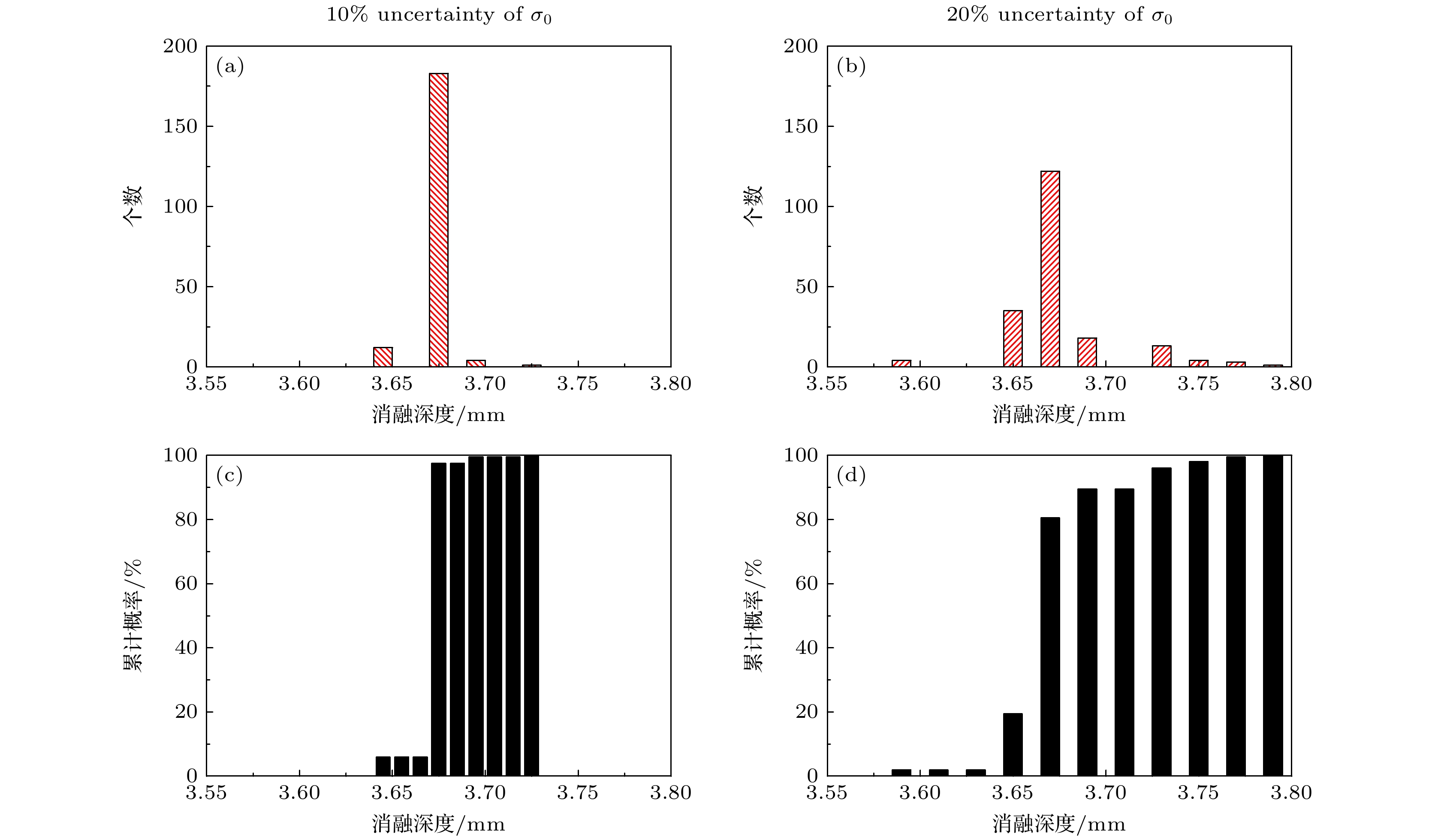
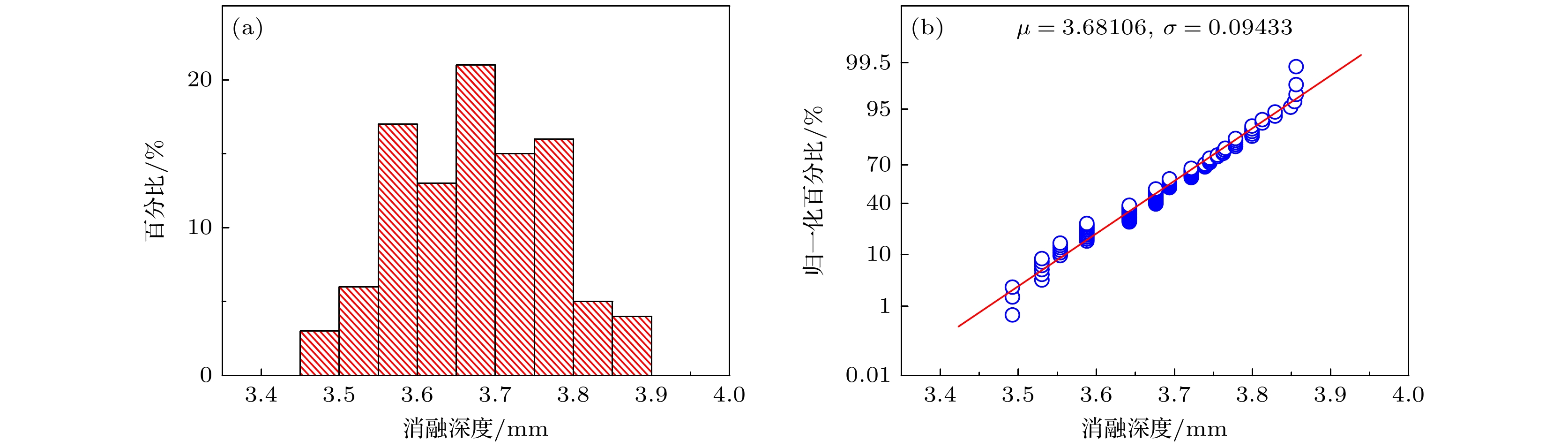
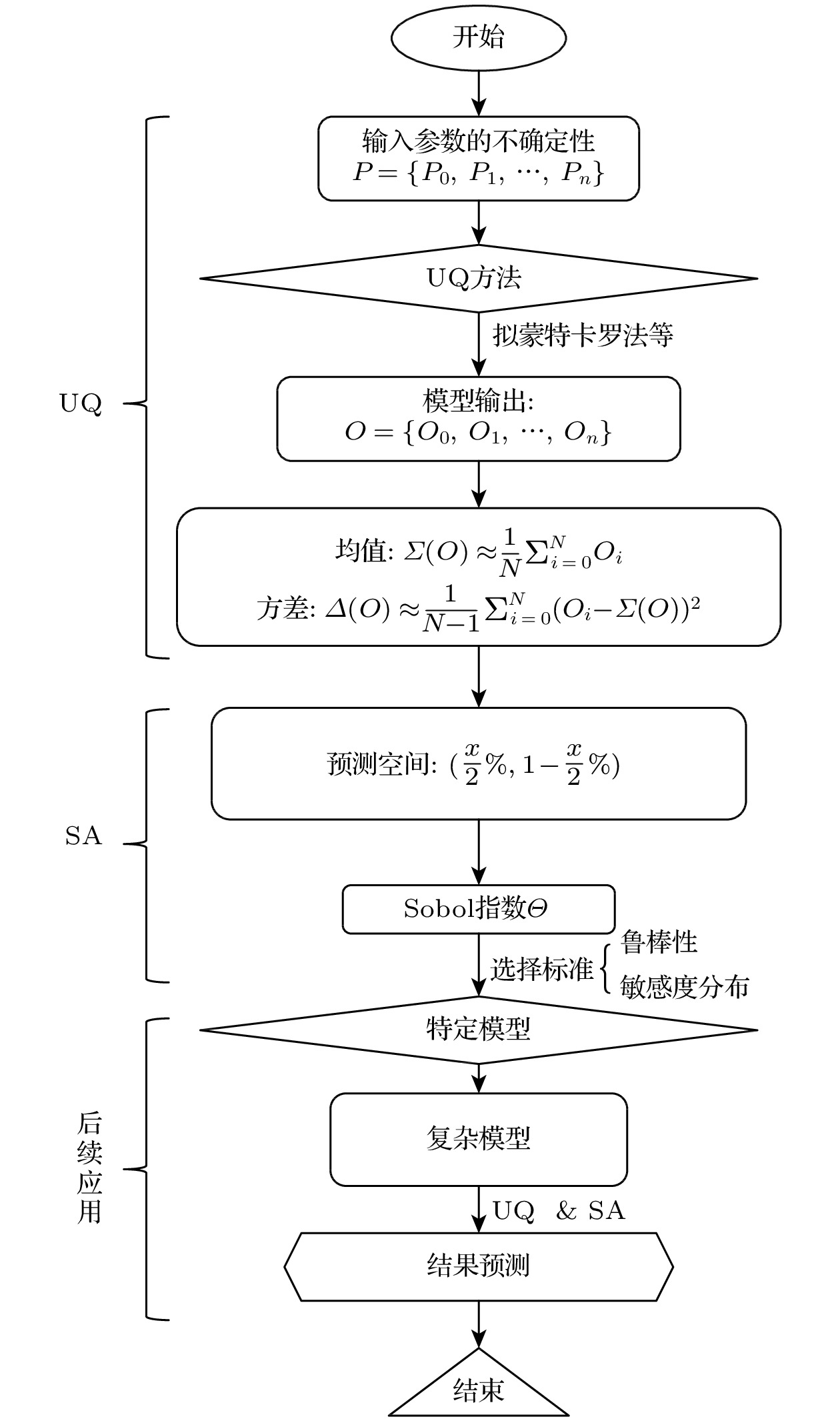
-
Pulsed field ablation (PFA) is a new type of physical energy source in the fields of tumor and atrial fibrillation ablation, which is based on irreversible electroporation with non-thermal, clear ablation boundaries, selective killing, and rapid advantages. The PFA triggers off the changes in the electrical conductivity of ablation zone, which can be described by a step function and used to predict the ablation zone. However, current research does not compare the advantages and disadvantages of different conductivity models, nor does it consider the effects of model parameter change caused by individual differences and errors on the efficacy of PFA. This work is devoted to comparing two commonly used conductivity models (Heaviside model and Gompertz model), and quantifying the influence of model input uncertainty on model output and PFA ablation zone. In this work, we carry out uncertainty quantification and sensitivity analysis to quantify the influence of model parameter uncertainty on model output, clarify the parameter sensitivity distribution, and provide model selection criteria from the perspectives of model complexity, parameter sensitivity distribution, and model robustness. Combined with finite element simulation, the study quantifies the effects of uncertainty in the most sensitive parameters of the conductivity model and ablation threshold on the PFA ablation zone. The results show that different conductivity models exhibit different robustness under the same proportion of variation in parameters. The Heaviside model, which is determined by a single factor, has strong robustness. The uncertainty output of the Gompertz model is jointly determined by multiple sensitivity parameters, making it susceptible to various conditions. The ablation threshold and pre-treatment tissue conductivity are the two most sensitive parameters affecting the assessment of ablation depth. Changes in the ablation threshold result in a Gaussian distribution of ablation depth. The greater the change in pre-treatment tissue conductivity, the greater the change in ablation depth is, which, however, follows a nonlinear proportional relationship. This approach can improve the accuracy and reliability of PFA ablation prediction, and provide a visual and global way to show the influence of input uncertainties on model output and parameter sensitivity ranking, thus effectively improving the accuracy of model prediction, reducing computational costs, and optimizing the selection of candidate models. This strategy can be applied to a variety of mathematical physics and simulation models to enhance model credibility and simplify the models. -
Keywords:
- conductivity model /
- sensitivity analysis /
- electroporation /
- pulsed field ablation
[1] Ivorra A, Al-Sakere B, Rubinsky B, Mir L M 2009 Phys. Med. Biol. 54 5949
Google Scholar
[2] Sel D, Cukjati D, Batiuskaite D, Slivnik T, Mir L M, Miklavcic D 2005 IEEE T. Bio-Med. Eng. 52 816
Google Scholar
[3] Garcia P A, Rossmeisl J H, Davalos R V 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society Guadalajara, Mexico, 30 Auguest–3 September, 2011 pp739–742
[4] Perera-Bel E, Aycock K N, Salameh Z S, Gómez-Barea M, Davalos R V, Ivorra A, Ballester M A G 2022 IEEE T. Bio-Med. Eng. 70 1902
[5] Neal R E, Garcia P A, Robertson J L, Davalos R V 2012 IEEE T. Bio-Med. Eng. 59 1076
Google Scholar
[6] Zhao Y, Bhonsle S, Dong S, Lyu Y, Liu H, Safaai-Jazi A, Davalos R V, Yao C 2018 IEEE T. Bio-Med. Eng. 65 1810
Google Scholar
[7] Shi F, Steuer A, Zhuang J, Kolb J F 2019 IEEE T. Bio-Med. Eng. 66 2010
Google Scholar
[8] 郭雨怡, 石富坤, 王群, 季振宇, 庄杰 2022 71 068701
Google Scholar
Guo Y Y, Shi F K, Wang Q, Ji Z Y, Zhuang J 2022 Acta Phys. Sin. 71 068701
Google Scholar
[9] Shi F, Kolb J F 2020 Biosens. Bioelectron. 157 112149
Google Scholar
[10] Bounik R, Cardes F, Ulusan H, Modena M M, Hierlemann A 2022 BMEF 2022 9857485
[11] Corovic S, Lackovic I, Sustaric P, Sustar T, Rodic T, Miklavcic D 2013 BioMed. Eng. OnLine 12 16
Google Scholar
[12] Zhao Y J, Davalos R V 2020 Appl. Phys. Lett. 117 143702
Google Scholar
[13] 姚陈果, 郑爽, 赵亚军, 刘红梅, 王艺麟, 董守龙 2020 高电压技术 46 1830
Yao C G, Zhen S, Zhao Y Z, Liu H M, Wang Y L, Dong S L 2020 High Voltage Engineering 46 1830 (in Chinese)
[14] Smith R C 2013 Uncertainty Quantification: Theory, Implementation, and Applications (Vol. 12) (Siam)
[15] Lai X, Wang S, Ma S, Xie J, Zheng Y 2020 Electrochimica Acta 330 135239
Google Scholar
[16] Vazquez-Arenas J, Gimenez L E, Fowler M, Han T, Chen S K 2014 Energ. Convers. Manage. 87 472
Google Scholar
[17] Edouard C, Petit M, Forgez C, Bernard J, Revel R 2016 JOPS 325 482
[18] Ye X, Liu S, Yin H, He Q, Xue Z, Lu C, Su S 2021 Front. Cardiovasc. Med. 8
[19] 张家明 陈志坚 2022 临床心血管病杂志 38 851
Zhang J M, Chen Z J 2022 J Clin. Cardiol. 38 851
[20] O’Brien T J, Lorenzo M F, Zhao Y, Neal Ii R E, Robertson J L, Goldberg S N, Davalos R V 2019 Int. J. Hyperther. 36 952
Google Scholar
[21] Lemieux C 2009 Monte Carlo and Quasi-Monte Carlo Sampling (Springer, New York, NY)
[22] Haemmerich D, Schutt D J, Wright A S, Webster J G, Mahvi D M 2009 Physiol. Meas. 30 459
Google Scholar
[23] Sobol′ I M 2001 Math. Comput. Simulat. 55 271
Google Scholar
[24] Oliveira J F, Jorge D C P, Veiga R V, Rodrigues M S, Torquato M F, da Silva N B, Fiaccone R L, Cardim L L, Pereira F A C, de Castro C P, Paiva A S S, Amad A A S, Lima E A B F, Souza D S, Pinho S T R, Ramos P I P, Andrade R F S 2021 Nat. Commun. 12 333
Google Scholar
[25] Kaminska I, Kotulska M, Stecka A, Saczko J, Drag-Zalesinska M, Wysocka T, Choromanska A, Skolucka N, Nowicki R, Marczak J, Kulbacka J 2012 Gen. Physiol. Biophys. 31 19
Google Scholar
[26] Reddy V Y, Koruth J, Jais P, Petru J, Timko F, Skalsky I, Hebeler R, Labrousse L, Barandon L, Kralovec S, Funosako M, Mannuva B B, Sediva L, Neuzil P 2018 JACC: Clin. Electrophy. 4 987
Google Scholar
[27] Belalcazar A 2021 Heart Rhythm 2 560
Google Scholar
[28] Kos B, Zupanic A, Kotnik T, Snoj M, Sersa G, Miklavcic D 2010 J. Membrane Biol. 236 147
Google Scholar
[29] Shi F, Zhuang J, Kolb J F 2019 J. Phys. D 52 495401
Google Scholar
[30] Perera-Bel E, Mercadal B, Garcia-Sanchez T, Ballester M A G, Ivorra A 2021 IEEE T. Bio-Med. Eng. 68 1318
-
图 1 1/6三维PVI脉冲电场消融模型
Figure 1. One-sixth three-dimensional PVI pulsed electric field ablation model.
图 2 H模型和G模型的电导率输出的平均值、标准差和90%预测空间
Figure 2. Mean value, standard deviation, and 90% prediction space of conductivity output of H and G models.
图 3 H模型 和 G 模型的各参数一阶Sobol敏感度指数和平均Sobol指数
Figure 3. First order Sobol sensitivity index and average Sobol index of each parameter of the H and G models.
图 4 三维PVI消融模型的电场分布
Figure 4. Electric field distribution of three-dimensional PVI ablation model.
图 5 改变σ0, 不确定度分别为10% ((a), (c))和20% ((b), (d))时, 消融深度的统计结果
Figure 5. The statistical results of the ablation depth by changing σ0 with uncertainty of 10% ((a), (c)) and 20%((b), (d)).
图 6 消融阈值的均匀分布导致消融深度呈高斯分布
Figure 6. The uniform distribution of the ablation threshold results in a Gaussian distribution of the ablation depth.
图 7 用于多模型评估的UQ和SA示意图
Figure 7. Schematic diagram for UQ and SA for multi-model evaluation.
表 1 不同模型的参数
Table 1. Parameters for different models
参数 模型 Heaviside Gompertz σ0/(S·m–1) 0.23 0.23 α 0.02 0.02 T0/℃ 37 37 T/℃ 40 40 E0/(V·cm–1) 850 — E1/(V·cm–1 ） 1550 — W 0.90 — σm/(S·m–1) — 0.44 Ei/(V·cm–1） — 870 Em/(V·cm–1) — 1038 D — 18 
DownLoad: CSV
-
[1] Ivorra A, Al-Sakere B, Rubinsky B, Mir L M 2009 Phys. Med. Biol. 54 5949
Google Scholar
[2] Sel D, Cukjati D, Batiuskaite D, Slivnik T, Mir L M, Miklavcic D 2005 IEEE T. Bio-Med. Eng. 52 816
Google Scholar
[3] Garcia P A, Rossmeisl J H, Davalos R V 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society Guadalajara, Mexico, 30 Auguest–3 September, 2011 pp739–742
[4] Perera-Bel E, Aycock K N, Salameh Z S, Gómez-Barea M, Davalos R V, Ivorra A, Ballester M A G 2022 IEEE T. Bio-Med. Eng. 70 1902
[5] Neal R E, Garcia P A, Robertson J L, Davalos R V 2012 IEEE T. Bio-Med. Eng. 59 1076
Google Scholar
[6] Zhao Y, Bhonsle S, Dong S, Lyu Y, Liu H, Safaai-Jazi A, Davalos R V, Yao C 2018 IEEE T. Bio-Med. Eng. 65 1810
Google Scholar
[7] Shi F, Steuer A, Zhuang J, Kolb J F 2019 IEEE T. Bio-Med. Eng. 66 2010
Google Scholar
[8] 郭雨怡, 石富坤, 王群, 季振宇, 庄杰 2022 71 068701
Google Scholar
Guo Y Y, Shi F K, Wang Q, Ji Z Y, Zhuang J 2022 Acta Phys. Sin. 71 068701
Google Scholar
[9] Shi F, Kolb J F 2020 Biosens. Bioelectron. 157 112149
Google Scholar
[10] Bounik R, Cardes F, Ulusan H, Modena M M, Hierlemann A 2022 BMEF 2022 9857485
[11] Corovic S, Lackovic I, Sustaric P, Sustar T, Rodic T, Miklavcic D 2013 BioMed. Eng. OnLine 12 16
Google Scholar
[12] Zhao Y J, Davalos R V 2020 Appl. Phys. Lett. 117 143702
Google Scholar
[13] 姚陈果, 郑爽, 赵亚军, 刘红梅, 王艺麟, 董守龙 2020 高电压技术 46 1830
Yao C G, Zhen S, Zhao Y Z, Liu H M, Wang Y L, Dong S L 2020 High Voltage Engineering 46 1830 (in Chinese)
[14] Smith R C 2013 Uncertainty Quantification: Theory, Implementation, and Applications (Vol. 12) (Siam)
[15] Lai X, Wang S, Ma S, Xie J, Zheng Y 2020 Electrochimica Acta 330 135239
Google Scholar
[16] Vazquez-Arenas J, Gimenez L E, Fowler M, Han T, Chen S K 2014 Energ. Convers. Manage. 87 472
Google Scholar
[17] Edouard C, Petit M, Forgez C, Bernard J, Revel R 2016 JOPS 325 482
[18] Ye X, Liu S, Yin H, He Q, Xue Z, Lu C, Su S 2021 Front. Cardiovasc. Med. 8
[19] 张家明 陈志坚 2022 临床心血管病杂志 38 851
Zhang J M, Chen Z J 2022 J Clin. Cardiol. 38 851
[20] O’Brien T J, Lorenzo M F, Zhao Y, Neal Ii R E, Robertson J L, Goldberg S N, Davalos R V 2019 Int. J. Hyperther. 36 952
Google Scholar
[21] Lemieux C 2009 Monte Carlo and Quasi-Monte Carlo Sampling (Springer, New York, NY)
[22] Haemmerich D, Schutt D J, Wright A S, Webster J G, Mahvi D M 2009 Physiol. Meas. 30 459
Google Scholar
[23] Sobol′ I M 2001 Math. Comput. Simulat. 55 271
Google Scholar
[24] Oliveira J F, Jorge D C P, Veiga R V, Rodrigues M S, Torquato M F, da Silva N B, Fiaccone R L, Cardim L L, Pereira F A C, de Castro C P, Paiva A S S, Amad A A S, Lima E A B F, Souza D S, Pinho S T R, Ramos P I P, Andrade R F S 2021 Nat. Commun. 12 333
Google Scholar
[25] Kaminska I, Kotulska M, Stecka A, Saczko J, Drag-Zalesinska M, Wysocka T, Choromanska A, Skolucka N, Nowicki R, Marczak J, Kulbacka J 2012 Gen. Physiol. Biophys. 31 19
Google Scholar
[26] Reddy V Y, Koruth J, Jais P, Petru J, Timko F, Skalsky I, Hebeler R, Labrousse L, Barandon L, Kralovec S, Funosako M, Mannuva B B, Sediva L, Neuzil P 2018 JACC: Clin. Electrophy. 4 987
Google Scholar
[27] Belalcazar A 2021 Heart Rhythm 2 560
Google Scholar
[28] Kos B, Zupanic A, Kotnik T, Snoj M, Sersa G, Miklavcic D 2010 J. Membrane Biol. 236 147
Google Scholar
[29] Shi F, Zhuang J, Kolb J F 2019 J. Phys. D 52 495401
Google Scholar
[30] Perera-Bel E, Mercadal B, Garcia-Sanchez T, Ballester M A G, Ivorra A 2021 IEEE T. Bio-Med. Eng. 68 1318
DownLoad:
Catalog
Metrics
- Abstract views: 3563
- PDF Downloads: 73
- Cited By: 0
