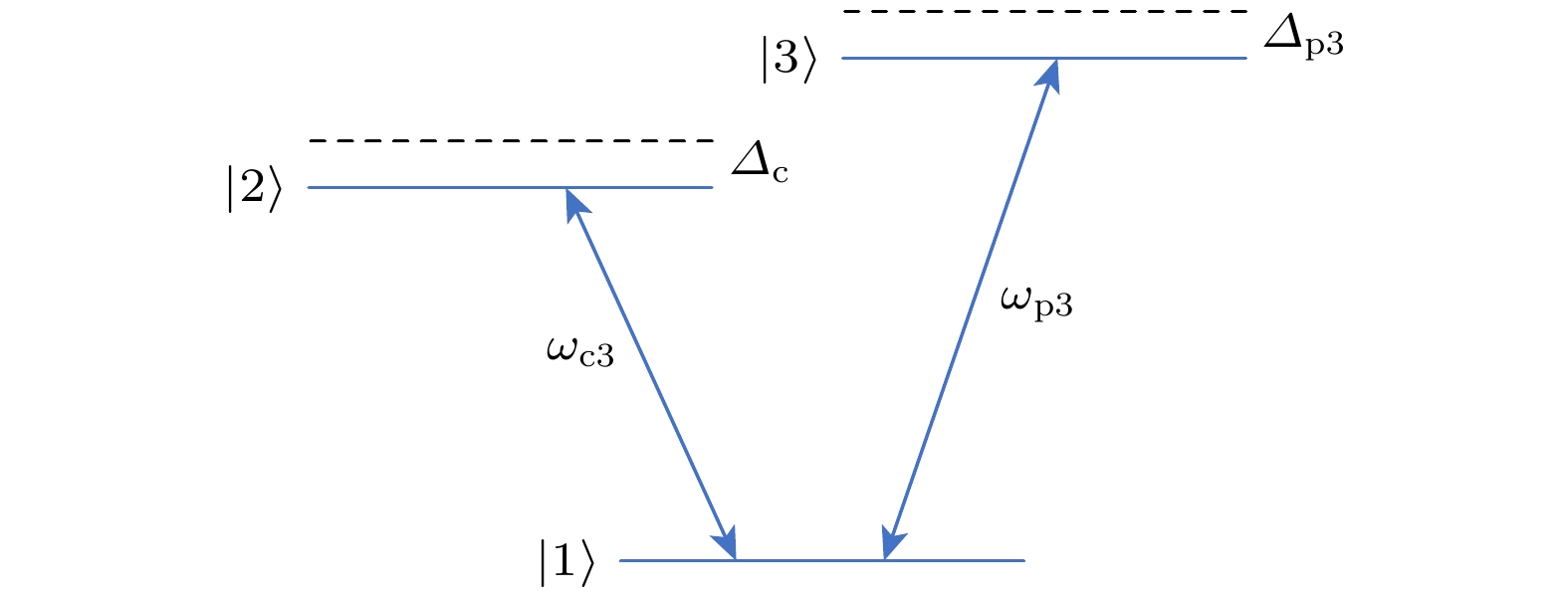
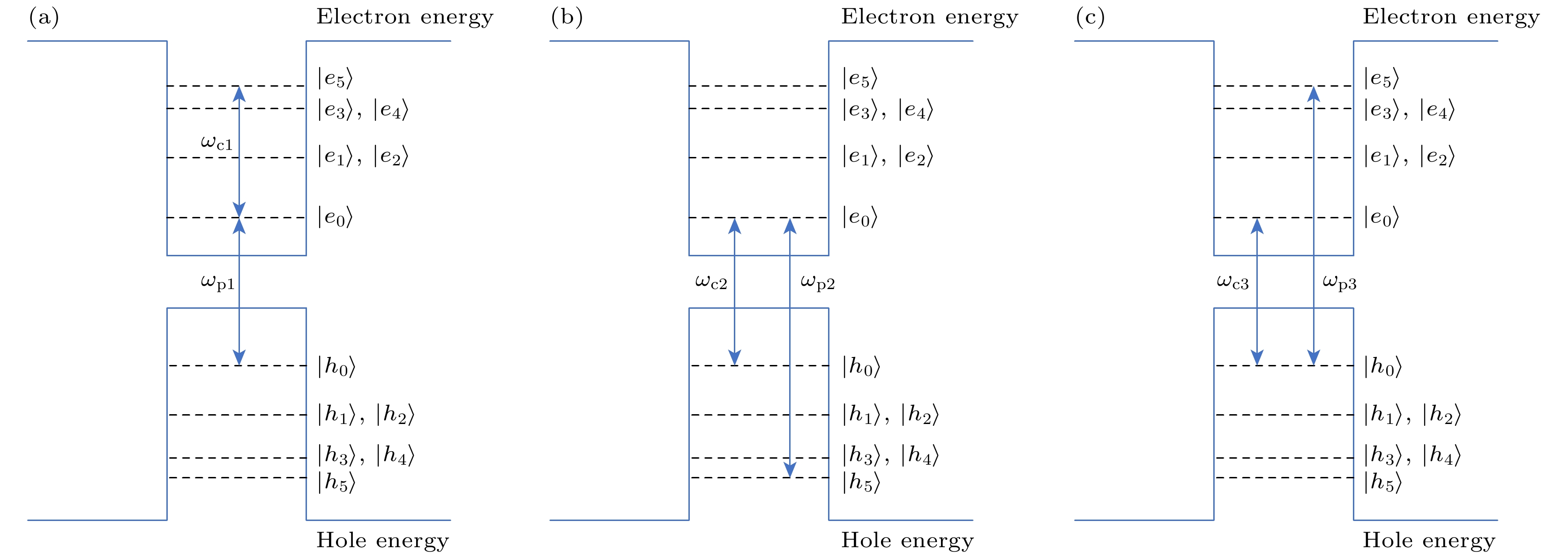
-
Based on the current growth technology of quantum dot in the experiment, considering that the probe fields and control fields at different frequencies are coupled between different energy levels of the InAs/GaAs quantum dot, the ladder-type, Λ-type and V-type energy level configurations can be formed. The linear and nonlinear properties of these energy level configurations of InAs/GaAs quantum dots are studied by using semiclassical theory combined with multiple scale method. It is shown that in the linear case, electromagnetic induction transparency windows can be formed among ladder-type, Λ-type and V-type energy level configurations. And the width of the transparent window increases with the strength of the control pulse increasing. For the nonlinear case, under the current experimental condition, optical solitons can be formed and stored in ladder-type configuration and
$ {{\Lambda }} $ -type energy level configuration. However, optical solitons cannot be formed in the V-type energy level configurations, which is because the nonlinear effect of the system is very weak. Furthermore, it is demonstrated that the fidelity of the storage and retrieval of the optical solitons is higher than that of linear optical pulse and strongly nonlinear optical pulse. Interestingly, it is also found that the amplitude of stored optical solitons in$ {{\Lambda }} $ -type energy level configuration is higher than that in ladder-type energy level configuration. This study provides a theoretical basis for semiconductor quantum dot devices to modulate the amplitude of the stored optical solitons.-
Keywords:
- electromagnetically induced transparency /
- storage and retrieval of optical solitons /
- semiconductor quantum dot
[1] Kivshar Y S, Agrawal G 2003 Optical Solitons: From Fibers to Photonic Crystals (New York: Academic Press)
[2] Dauxois T, Peyrard M 2006 Physics of Solitons (Cambridge: Cambridge University Press)
[3] Wang Y, Ding J W, Wang D L, Liu W M 2020 Chaos 30 123133
Google Scholar
[4] Song W W, Li Q Y, Li Z D, Fu G S 2010 Chin. Phys. B 19 070503
Google Scholar
[5] Zhang X F, Zhang P, He W Q, Lin X X 2011 Chin. Phys. B 20 020307
Google Scholar
[6] Li Z D, Guo Q Q, Guo Y, He P B, Liu W M 2021 Chin. Phys. B 30 107506
Google Scholar
[7] Guo H, Qiu X, Ma Y, Jiang H F, Zhang X F 2021 Chin. Phys. B 30 060310
Google Scholar
[8] Li Z D, Wang Y Y, He P B 2019 Chin. Phys. B 28 010504
Google Scholar
[9] Harris S E 1997 Phys. Today 50 36
[10] Fleischhauer M, Imamoglu A, Marangos J P 2005 Rev. Mod. Phys. 77 633
Google Scholar
[11] Hang C, Huang G X 2008 Phys. Rev. A 77 033830
Google Scholar
[12] Huang G X, Deng L, Payne M G 2005 Phys. Rev. E 72 016617
Google Scholar
[13] Li H J, Huang G X 2008 Phys. Lett. A 372 4127
Google Scholar
[14] Wu Y, Deng L 2004 Phys. Rev. Lett. 93 143904
Google Scholar
[15] Dong Y Y, Wang D L, Wang Y, Ding J W 2018 Phys. Lett. A 382 2006
Google Scholar
[16] Chen Y, Bai Z Y, Huang G X 2014 Phys. Rev. A 89 023835
Google Scholar
[17] Chen Y, Chen Z M, Huang G X 2015 Phys. Rev. A 91 023820
Google Scholar
[18] Shou C, Huang G X 2019 Phys. Rev. A 99 043821
Google Scholar
[19] Chen Z M, Bai Z Y, Li H J, Hang C, Huang G X 2015 Sci. Rep. 5 8211
Google Scholar
[20] 朱天伟, 徐波, 何军, 赵凤瑷, 张春玲, 谢二庆, 刘峰奇, 王占国 2004 53 301
Google Scholar
Zhu T W, Xu B, He J, Zhao F A, Zhang C L, Xie E Q, Liu F Q, Wang Z G 2004 Acta Phys. Sin. 53 301
Google Scholar
[21] Lodahl P, Mahmoodian S, Stobbe S 2015 Rev. Mod. Phys. 87 347
Google Scholar
[22] 谭康伯, 路宏敏, 官乔, 张光硕, 陈冲冲 2018 67 064207
Google Scholar
Tan K B, Lu H M, Guan Q, Zhang G S, Chen C C 2018 Acta Phys. Sin. 67 064207
Google Scholar
[23] 田芃, 黄黎蓉, 费淑萍, 余奕, 潘彬, 徐巍, 黄德修 2010 59 5738
Google Scholar
Tian P, Huang L R, Fei S P, Y Yi, Pan B, Xu W, Huang D X 2010 Acta Phys. Sin. 59 5738
Google Scholar
[24] Hasnain C C J, Cheng P K, Jungho K, Chuang S L 2003 Proc. IEEE 9 1884
Google Scholar
[25] Kraus R M, Lagoudakis P G, Rogach A L, Talapin D V, Weller H, Lupton J M, Feldmann J 2007 Phys. Rev. Lett. 98 017401
Google Scholar
[26] Krenner H J, Pryor C E, He J, Petroff P M 2008 Nano Lett. 8 1750
Google Scholar
[27] Ramsay A J, Boyle S J, Kolodka R S, Oliveira J B B, Szymanska J S, Liu H Y, Hopkinson M, Fox A M, Skolnick M S 2008 Phys. Rev. Lett. 100 197401
Google Scholar
[28] 唐宏, 王登龙, 张蔚曦, 丁建文, 肖思国 2017 66 034202
Google Scholar
Tang H, Wang D L, Zhang W X, Ding J W, Xiao S G 2017 Acta. Phys. Sin. 66 034202
Google Scholar
[29] 杨璇, 王胤, 王登龙, 丁建文 2020 69 174203
Google Scholar
Yang X, Wang Y, Wang D L, Ding J W 2020 Acta Phys. Sin. 69 174203
Google Scholar
[30] Wang Y, Ding J W, Wang D L 2020 Eur. Phys. J. D 74 190
Google Scholar
[31] Zhou S J, Wang D L, Dong Y Y, Bai Z Y, Ding J W 2022 Phys. Lett. A 448 128320
Google Scholar
[32] Yang W X, Chen A X, Lee R K, Wu Y 2011 Phys. Rev. A 84 013835
Google Scholar
[33] 曾宽宏, 王登龙, 佘彦超, 张蔚曦 2013 62 147801
Google Scholar
Zeng K H, Wang D L, She Y C, Zhang W X 2013 Acta. Phys. Sin. 62 147801
Google Scholar
[34] Antón M A, Carreño F, Calderón O G, Melle S 2008 Opt. Commun. 281 3301
Google Scholar
[35] Gerardot B D, Brunner D, Dalgarno P A, Karrai K, Badolato A, Petroff P M, Warburton R J 2009 New J. Phys. 11 013028
Google Scholar
[36] Khaledi N A, Sabaeian M, Sahrai M, Fallahi V 2014 J. Opt. 16 055004
Google Scholar
[37] Ku P C, Hasnain C C J, Chuang S L 2007 J. Phys. D 40 R93
Google Scholar
[38] Khursan A A H, Khakani A M K, Mossawi A K H 2009 Photon. Nanostruct. Fundam. Appl. 7 153
Google Scholar
[39] Abdullah M, Noori F T M, Khursan A A H 2015 Superlattices Microstruct. 82 219
Google Scholar
[40] Houmark J, Nielsen T R, Mørk J, Jauho A P 2009 Phys. Rev. B 79 115420
Google Scholar
-
图 1 半导体量子点的三能级构型机理示意图 (a)梯形; (b)
$ {{\Lambda }} $ 形; (c) V形Figure 1. Schematic diagram of three energy level in the semiconductor quantum dot: (a) Ladder-type; (b)
$ {{\Lambda }} $ -type energy; (c) V-type.
图 2 梯形三能级量子点EIT构型示意图
Figure 2. Schematic diagram of ladder-type three energy level in the quantum dot EIT configuration.
图 3 在不同控制光强
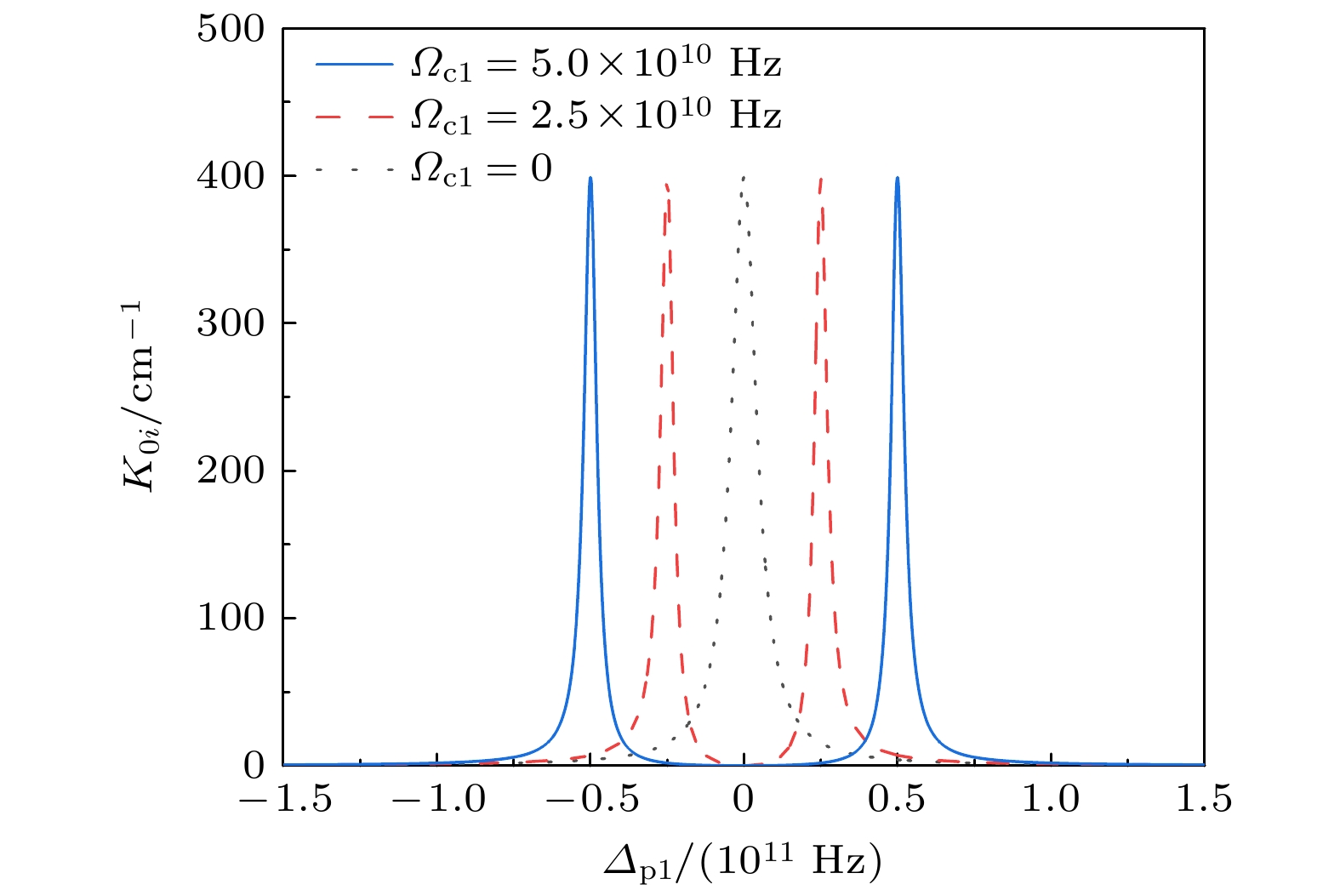
$ {\varOmega }_{{\rm{c}}1} $ 下体系对探测光的吸收谱线图. 图中所用其他参数为${\gamma }_{21}=3.3\;{\rm{μ}}{\rm{e}}{\rm{V}}$ ,${\gamma }_{31}=3.3\times $ $ {10}^{-4}\;{\rm{μ }}{\rm{e}}{\rm{V}}$ ,${\kappa }_{12}=1317{{\rm{c}}{\rm{m}}}^{-1}\;{\rm{μ}}{\rm{e}}{\rm{V}}$ Figure 3. The linear absorption coefficient
$ {K}_{0{\rm{i}}} $ as a function of the detuning${\varDelta }_{{\rm{p}}1}$ with different control fields${\varOmega }_{{\rm{c}}1}$ . Other parameters used are${\gamma }_{21}=3.3\;{\rm{μ}}{\rm{e}}{\rm{V}}$ ,${\gamma }_{31}=3.3\times {10}^{-4}\;{\rm{μ }}{\rm{e}}{\rm{V}}$ , and${\kappa }_{12}=1317\;{{\rm{c}}{\rm{m}}}^{-1}\;{\rm{μ }}{\rm{e}}{\rm{V}}$ , respectively.
图 4 透明窗口区域内光孤子的传播. 光孤子波形
${|{\varOmega }_{{\rm{p}}1}/{U}_{0}|}^{2}$ 随${z}/{L}_{{\rm{D}}}$ 和$ t/{\tau }_{0} $ 的变化情况Figure 4. The propagation of the optical soliton in the rang of the transparency window. Wave shape
${|{\varOmega }_{{\rm{p}}1}/{U}_{0}|}^{2}$ as a function of${z}/{L}_{{\rm{D}}}$ and$ t/{\tau }_{0} $ .
图 5 不同强度的光强下, 探测光
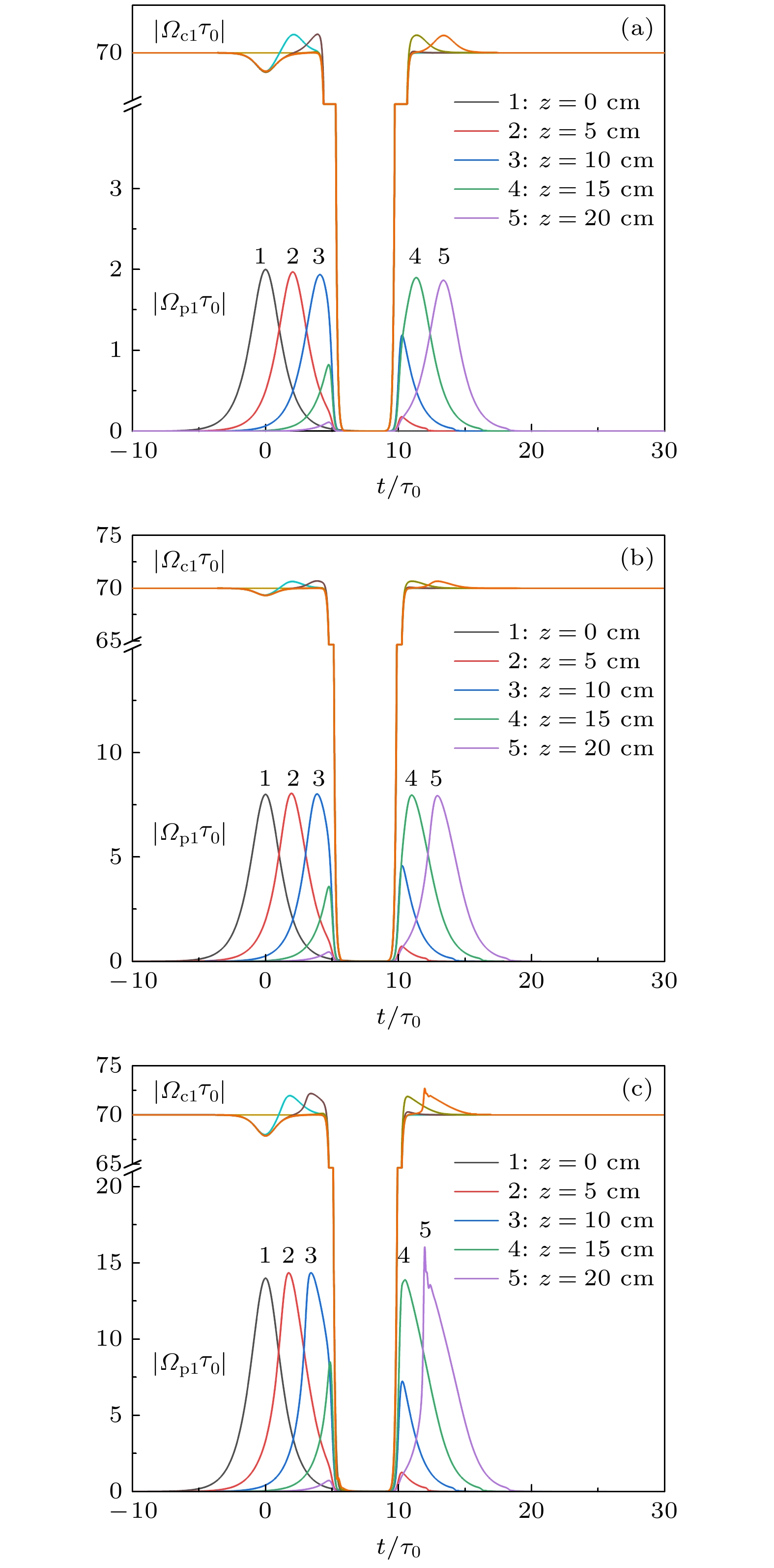
$ \left|{\varOmega }_{{\rm{p}}1}{\tau }_{0}\right| $ 和控制光$ \left|{\varOmega }_{{\rm{c}}1}{\tau }_{0}\right| $ 随时间$ t $ 和传播距离$ {z} $ 的变化情况 (a)弱探测光的存储与读取,$ {\varOmega }_{{\rm{p}}1}(0, t)=2{\rm{s}}{\rm{e}}{\rm{c}}{\rm{h}}\left(t/{\tau }_{0}\right) $ ; (b)光孤子的存储与读取,$ {\varOmega }_{{\rm{p}}1}(0, t)=8{\rm{s}}{\rm{e}}{\rm{c}}{\rm{h}}\left(t/{\tau }_{0}\right) $ ; (c)强探测光的存储与读取,$ {\varOmega }_{{\rm{p}}1}(0, t)=14{\rm{s}}{\rm{e}}{\rm{c}}{\rm{h}}\left(t/{\tau }_{0}\right) $ .$\left|{\varOmega }_{{\rm{c}}1}{\tau }_{0}\right|$ 代表控制光的开、关. 线条1—5分别对应于$z=0, {\rm{ }}5, {\rm{ }}10, {\rm{ }}15, {\rm{ }}20\;{\rm{c}}{\rm{m}}$ Figure 5. Time evolution of
$ \left|{\varOmega }_{{\rm{p}}1}{\tau }_{0}\right| $ and$ \left|{\varOmega }_{c1}{\tau }_{0}\right| $ as functions of z and t for different input light intensities: (a) Storage and retrieval of a weak probe pulse, with${\varOmega }_{{\rm{p}}1}(0, t)= $ $ 2{\rm{s}}{\rm{e}}{\rm{c}}{\rm{h}}\left(t/{\tau }_{0}\right)$ ; (b) storage and retrieval of an optical soliton, with$ {\varOmega }_{{\rm{p}}1}(0, t)=8{\rm{s}}{\rm{e}}{\rm{c}}{\rm{h}}\left(t/{\tau }_{0}\right) $ ; (c) storage and retrieval of a strong probe pulse, with$ {\varOmega }_{{\rm{p}}1}(0, t)=14{\rm{s}}{\rm{e}}{\rm{c}}{\rm{h}}\left(t/{\tau }_{0}\right) $ ;$ \left|{\varOmega }_{{\rm{c}}1}{\tau }_{0}\right| $ represents the switching off and on of the control pulse. Lines 1 to 5 in each panel correspond to$z=0, {\rm{ }}5, $ $ {\rm{ }}10, {\rm{ }}15, {\rm{ }}20\;{\rm{ }}{\rm{c}}{\rm{m}}$ , respectively.
图 6
$ {{\Lambda }} $ 形三能级量子点EIT构型示意图Figure 6. Schematic diagram of
$ {{\Lambda }} $ -type three energy level in the quantum dot EIT configuration.
图 7 在不同强度
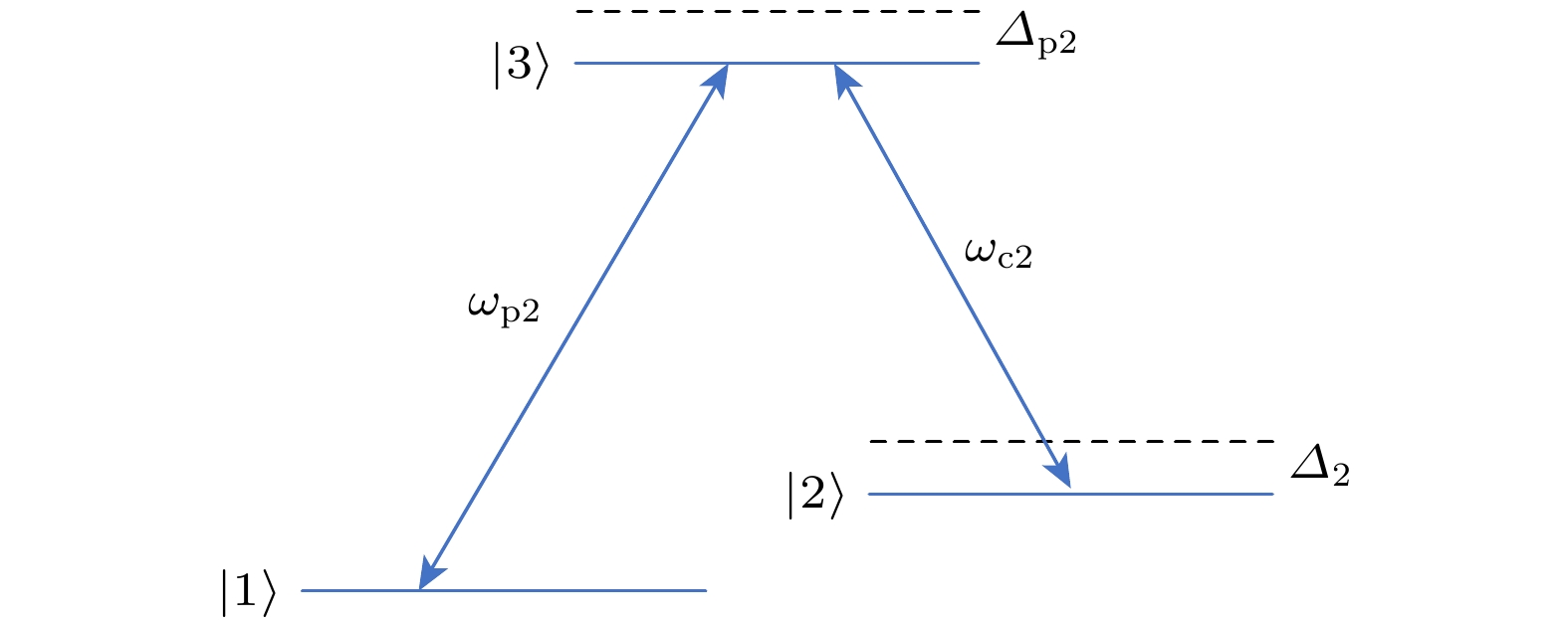
${\varOmega }_{{\rm{c}}2}$ 下体系对探测脉冲的吸收谱线图, 其中${\gamma }_{32}=3.3\;{\rm{μ}}{\rm{e}}{\rm{V}}$ ,${\gamma }_{21}=3.3\times {10}^{-4}\;{\rm{μ }}{\rm{e}}{\rm{V}}$ ,${\gamma }_{13}= $ $ 1976\;{{\rm{c}}{\rm{m}}}^{-1}\;{\rm{μ}}{\rm{e}}{\rm{V}}$ .Figure 7. Linear absorption coefficient
$ {K}_{0{\rm{i}}} $ as a function of the detuning$ {\Delta }_{{\rm{p}}2} $ with different control fields${\varOmega }_{{\rm{c}}2},$ other parameters used are${\gamma }_{32}=3.3\;{\rm{μ}}{\rm{e}}{\rm{V}}$ ,${\gamma }_{21}=3.3\times {10}^{-4}\;{\rm{μ}}{\rm{e}}{\rm{V}}$ , and${\gamma }_{13}=1976\;{{\rm{c}}{\rm{m}}}^{-1}{\rm{μ }}{\rm{e}}{\rm{V}}$ , respectively.
图 8 光孤子的存储与读取,
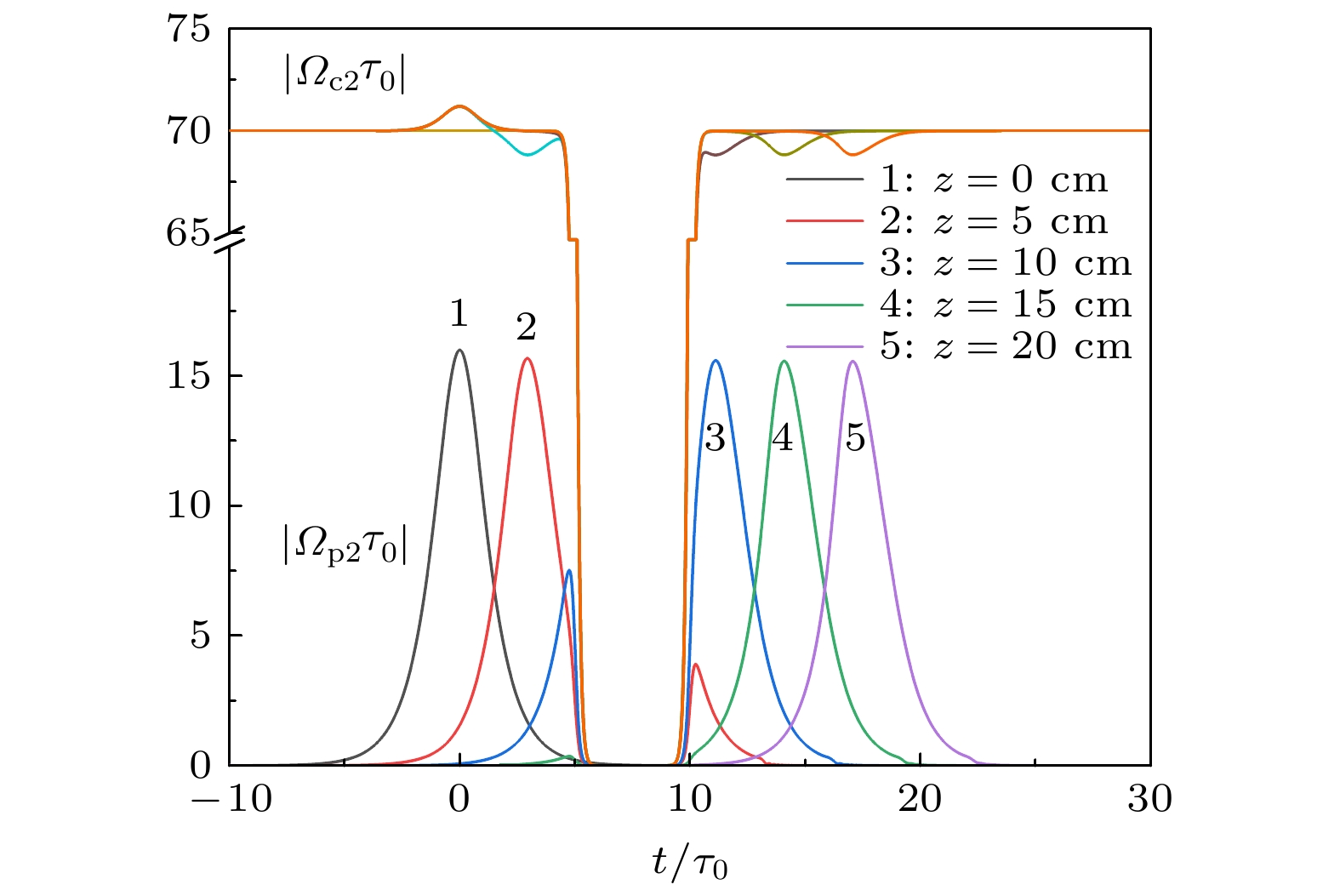
${\varOmega }_{{\rm{p}}2}\left(0, t\right)=16{\rm{sech}}\left(t/{\tau }_{0}\right)$ ,$\left|{\varOmega }_{{\rm{c}}2}{\tau }_{0}\right|$ 代表控制光的开、关, 线条1—5分别对应于$z=0, {\rm{ }}5, $ $ {\rm{ }}10, {\rm{ }}15, {\rm{ }}20\;{\rm{c}}{\rm{m}}$ Figure 8. Storage and retrieval of optical solitons,
${\varOmega }_{{\rm{p}}2}(0, t)=16{\rm{s}}{\rm{e}}{\rm{c}}{\rm{h}}\left(t/{\tau }_{0}\right)$ .$\left|{\varOmega }_{{\rm{c}}2}{\tau }_{0}\right|$ represents the switching off and on of the control pulse. Lines 1 to 5 represent$z=0, {\rm{ }}5, {\rm{ }}10, {\rm{ }}15, {\rm{ }}20\;{\rm{c}}{\rm{m}}$ , respectively.
图 9
$ {\rm{V}} $ 形三能级量子点EIT构型示意图Figure 9. Schematic diagram of
$ {\rm{V}} $ -type three energy level in the quantum dot EIT configuration.
图 10 在不同强度
${\varOmega }_{{\rm{c}}3}$ 下体系对探测光的吸收谱线图, 其中${\gamma }_{21}=3.3\;{\rm{μ }}{\rm{e}}{\rm{V}}$ ,${\gamma }_{32}=3.3\times {10}^{-4}\;{\rm{μ }}{\rm{e}}{\rm{V}}$ ,${\gamma }_{13}= $ $ 1976\;{{\rm{c}}{\rm{m}}}^{-1}\cdot{\rm{μ}}{\rm{e}}{\rm{V}}$ Figure 10. The linear absorption coefficient
$ {K}_{0 i} $ as a function of the detuning${\varDelta }_{{\rm{p}}3}$ with different control fields${\varOmega }_{{\rm{c}}3},$ where${\gamma }_{21}=3.3\;{\rm{μ}}{\rm{e}}{\rm{V}}$ ,${\gamma }_{32}=3.3\times {10}^{-4}\;{\rm{μ}}{\rm{e}}{\rm{V}}$ , and${\gamma }_{13}= $ $ 1976\;{{\rm{c}}{\rm{m}}}^{-1}\cdot{\rm{μ}}{\rm{e}}{\rm{V}}$ , respectively. -
[1] Kivshar Y S, Agrawal G 2003 Optical Solitons: From Fibers to Photonic Crystals (New York: Academic Press)
[2] Dauxois T, Peyrard M 2006 Physics of Solitons (Cambridge: Cambridge University Press)
[3] Wang Y, Ding J W, Wang D L, Liu W M 2020 Chaos 30 123133
Google Scholar
[4] Song W W, Li Q Y, Li Z D, Fu G S 2010 Chin. Phys. B 19 070503
Google Scholar
[5] Zhang X F, Zhang P, He W Q, Lin X X 2011 Chin. Phys. B 20 020307
Google Scholar
[6] Li Z D, Guo Q Q, Guo Y, He P B, Liu W M 2021 Chin. Phys. B 30 107506
Google Scholar
[7] Guo H, Qiu X, Ma Y, Jiang H F, Zhang X F 2021 Chin. Phys. B 30 060310
Google Scholar
[8] Li Z D, Wang Y Y, He P B 2019 Chin. Phys. B 28 010504
Google Scholar
[9] Harris S E 1997 Phys. Today 50 36
[10] Fleischhauer M, Imamoglu A, Marangos J P 2005 Rev. Mod. Phys. 77 633
Google Scholar
[11] Hang C, Huang G X 2008 Phys. Rev. A 77 033830
Google Scholar
[12] Huang G X, Deng L, Payne M G 2005 Phys. Rev. E 72 016617
Google Scholar
[13] Li H J, Huang G X 2008 Phys. Lett. A 372 4127
Google Scholar
[14] Wu Y, Deng L 2004 Phys. Rev. Lett. 93 143904
Google Scholar
[15] Dong Y Y, Wang D L, Wang Y, Ding J W 2018 Phys. Lett. A 382 2006
Google Scholar
[16] Chen Y, Bai Z Y, Huang G X 2014 Phys. Rev. A 89 023835
Google Scholar
[17] Chen Y, Chen Z M, Huang G X 2015 Phys. Rev. A 91 023820
Google Scholar
[18] Shou C, Huang G X 2019 Phys. Rev. A 99 043821
Google Scholar
[19] Chen Z M, Bai Z Y, Li H J, Hang C, Huang G X 2015 Sci. Rep. 5 8211
Google Scholar
[20] 朱天伟, 徐波, 何军, 赵凤瑷, 张春玲, 谢二庆, 刘峰奇, 王占国 2004 53 301
Google Scholar
Zhu T W, Xu B, He J, Zhao F A, Zhang C L, Xie E Q, Liu F Q, Wang Z G 2004 Acta Phys. Sin. 53 301
Google Scholar
[21] Lodahl P, Mahmoodian S, Stobbe S 2015 Rev. Mod. Phys. 87 347
Google Scholar
[22] 谭康伯, 路宏敏, 官乔, 张光硕, 陈冲冲 2018 67 064207
Google Scholar
Tan K B, Lu H M, Guan Q, Zhang G S, Chen C C 2018 Acta Phys. Sin. 67 064207
Google Scholar
[23] 田芃, 黄黎蓉, 费淑萍, 余奕, 潘彬, 徐巍, 黄德修 2010 59 5738
Google Scholar
Tian P, Huang L R, Fei S P, Y Yi, Pan B, Xu W, Huang D X 2010 Acta Phys. Sin. 59 5738
Google Scholar
[24] Hasnain C C J, Cheng P K, Jungho K, Chuang S L 2003 Proc. IEEE 9 1884
Google Scholar
[25] Kraus R M, Lagoudakis P G, Rogach A L, Talapin D V, Weller H, Lupton J M, Feldmann J 2007 Phys. Rev. Lett. 98 017401
Google Scholar
[26] Krenner H J, Pryor C E, He J, Petroff P M 2008 Nano Lett. 8 1750
Google Scholar
[27] Ramsay A J, Boyle S J, Kolodka R S, Oliveira J B B, Szymanska J S, Liu H Y, Hopkinson M, Fox A M, Skolnick M S 2008 Phys. Rev. Lett. 100 197401
Google Scholar
[28] 唐宏, 王登龙, 张蔚曦, 丁建文, 肖思国 2017 66 034202
Google Scholar
Tang H, Wang D L, Zhang W X, Ding J W, Xiao S G 2017 Acta. Phys. Sin. 66 034202
Google Scholar
[29] 杨璇, 王胤, 王登龙, 丁建文 2020 69 174203
Google Scholar
Yang X, Wang Y, Wang D L, Ding J W 2020 Acta Phys. Sin. 69 174203
Google Scholar
[30] Wang Y, Ding J W, Wang D L 2020 Eur. Phys. J. D 74 190
Google Scholar
[31] Zhou S J, Wang D L, Dong Y Y, Bai Z Y, Ding J W 2022 Phys. Lett. A 448 128320
Google Scholar
[32] Yang W X, Chen A X, Lee R K, Wu Y 2011 Phys. Rev. A 84 013835
Google Scholar
[33] 曾宽宏, 王登龙, 佘彦超, 张蔚曦 2013 62 147801
Google Scholar
Zeng K H, Wang D L, She Y C, Zhang W X 2013 Acta. Phys. Sin. 62 147801
Google Scholar
[34] Antón M A, Carreño F, Calderón O G, Melle S 2008 Opt. Commun. 281 3301
Google Scholar
[35] Gerardot B D, Brunner D, Dalgarno P A, Karrai K, Badolato A, Petroff P M, Warburton R J 2009 New J. Phys. 11 013028
Google Scholar
[36] Khaledi N A, Sabaeian M, Sahrai M, Fallahi V 2014 J. Opt. 16 055004
Google Scholar
[37] Ku P C, Hasnain C C J, Chuang S L 2007 J. Phys. D 40 R93
Google Scholar
[38] Khursan A A H, Khakani A M K, Mossawi A K H 2009 Photon. Nanostruct. Fundam. Appl. 7 153
Google Scholar
[39] Abdullah M, Noori F T M, Khursan A A H 2015 Superlattices Microstruct. 82 219
Google Scholar
[40] Houmark J, Nielsen T R, Mørk J, Jauho A P 2009 Phys. Rev. B 79 115420
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 3175
- PDF Downloads: 74
- Cited By: 0
