-
Compared with light, the solitons, which are from the balance between dispersion and nonlinearity of the system, possess high stability and fidelity as the information carries in quantum information processing and transmission, and have gained considerable attention in ultra-cold atomic electromagnetically induced transparent (EIT) media. To date, the EIT models on the three-level ultra-cold atoms realized experimentally, are ladder-, $\Lambda $ -, and V-type mode. Current studies show that the solitons cannot be stored in V-type three-level ultra-cold atomic EIT media but they can be stored in ladder- and$\Lambda $ -type three-level ultra-cold atomic EIT media. It is mainly because the atoms of the V-type system initially are in a excited state, while the atoms of the ladder- and$\Lambda $ -type systems initially are in the ground state. For the practical applications, it is a large challenge to control accurately the solitons stored in the ultra-cold atomic EIT media due to their ultralow temperature and rarefaction. Fortunately, with the maturity of semiconductor quantum technology, quantum dots have extensively application prospect in quantum information processing and transmission. However, the solitons cannot be stored in V-type three level InAs/GaAs quantum dot EIT media either, while it can be stored in ladder-type system and$\Lambda $ -type system.Therefore, herein we propose a V-type three-level nitrogen-vacancy (NV) center EIT model in which a weakprobe field and a strong control field are coupled to different energy levels of NV center in diamond. Subsequently, the linear and nonlinear properties of system are studied by using semiclassical theory combined with multi-scale method. It is shown that when control field is turned on, the linear absorption curve of the system presents an EIT window. And the width of the EIT window increases with the strength of magnetic induction of the control field increasing. In the nonlinear case, the solitons formed can stably propagate over a long distance. Interestingly, the solitons can be stored and retrieved by switching off and on the magnetic field of control field. Moreover, the amplitude of the stored solitons can be modulated by the magnetic induction strength of control field. This result indicates that solitons as information carriers in quantum information processing and transmission of NV center can greatly improve the fidelity of information processing. -
Keywords:
- nitrogen vacancy in diamond /
- storage and retrieval of solitons /
- electromagnetically induced transparency
[1] Haus H A, Wong W S 1996 Rev. Mod. Phys. 68 423
Google Scholar
[2] Wu Y, Deng L 2004 Phys. Rev. Lett. 93 143904
Google Scholar
[3] Huang G, Jiang K, Payne M G, Deng L 2006 Phys. Rev. E 73 056606
Google Scholar
[4] 任波, 佘彦超, 徐小凤, 叶伏秋 2021 70 224205
Google Scholar
Ren B, She Y C, Xu X F, Ye F Q 2021 Acta Phys. Sin. 70 224205
Google Scholar
[5] 高洁, 杭超 2022 71 133202
Google Scholar
Gao J, Hang C 2022 Acta Phys. Sin. 71 133202
Google Scholar
[6] Dong Y Y, Wang D L, Wang Y, Ding J W 2018 Phys. Lett. A 382 2006
Google Scholar
[7] Zhang X F, Yang Q, Zhang J F, Chen X Z, Liu W M 2008 Phys. Rev. A 77 023613
Google Scholar
[8] Wang Y, Ding J W, Wang D L 2020 Eur. Phys. J. D 74 190
Google Scholar
[9] Harris S E 1997 Phys. Today 50 36
[10] Fleischhauer M, Imamoglu A, Marangos J P 2005 Rev. Mod. Phys. 77 633
Google Scholar
[11] Huang G, Deng L, Payne M G 2005 Phys. Rev. E 72 016617
Google Scholar
[12] Hang C, Huang G X 2008 Phys. Rev. A 77 033830
Google Scholar
[13] Shou C, Huang G X 2019 Phys. Rev. A 99 043821
Google Scholar
[14] Bai Z Y, Hang C, Huang G X 2013 Chin. Opt. Lett. 11 012701
Google Scholar
[15] Chen Y, Bai Z Y, Huang G X 2014 Phys. Rev. A 89 023835
Google Scholar
[16] Wu Y, Yang X X 2005 Phys. Rev. A 71 053806
Google Scholar
[17] 王胤, 周驷杰, 陈桥, 邓永和 2023 72 084204
Google Scholar
Wang Y, Zhou S J, Chen Q, Deng Y H 2023 Acta Phys. Sin. 72 084204
Google Scholar
[18] Li P B, Xiang Z L, Rabl P, Nori F 2016 Phys. Rev. Lett. 117 015502
Google Scholar
[19] Doherty M W, Manson N B, Delaney P, Jelezko F, Wrachtrup J, Hollenberg L C L 2013 Phys. Rep. 528 1
Google Scholar
[20] Robledo L, Bernien H, Sar T V D, Hanson R 2011 New J. Phys. 13 025013
Google Scholar
[21] Yang W L, Yin Z Q, Hu Y, Feng M, Du J F 2011 Phys. Rev. A 84 010301
Google Scholar
[22] Lee D, Lee K W, Cady J V, Ovartchaiyapong P, Jayich A C B 2017 J. Opt. 19 033001
Google Scholar
[23] Ghaderi Goran Abad M, Mahmoudi M 2019 Eur. Phys. J. D 73 1
Google Scholar
[24] Yang X Y, Zhang N, Yuan H, Bian G D, Fan P C, Li M X 2019 AIP Adv. 9 075213
Google Scholar
[25] Lü X Y, Xiang Z L, Cui W, You J Q, Nori F 2013 Phys. Rev. A 88 012329
Google Scholar
[26] Grezes C, Julsgaard B, Kubo Y, Stern M, Umeda T, Isoya J, Sumiya H, Abe H, Onoda S, Ohshima T, Jacques V, Esteve J, Vion D, Esteve D, Mølmer K, Bertet P 2014 Phys. Rev. X 4 021049
[27] Dutt M V, Childress L, Jiang L, Togan E, Maze J, Jelezko F, Zibrov A S, Hemmer P R, Lukin M D 2007 Science 316 1312
Google Scholar
[28] Zhang M Q, Zheng A S, Chen Q L, Liu J B 2020 Optik 218 165255
Google Scholar
[29] Liu Y, Raza F, Li K, Ullah H, Zhang Y, Zhang W, Zhao W 2019 J. Opt. Soc. Am. B: Opt. Phys. 36 002727
[30] 吴建冬, 程智, 叶翔宇, 李兆凯, 王鹏飞, 田长麟, 陈宏伟 2022 71 117601
Google Scholar
Wu J D, Cheng Z, Ye X Y, Li Z K, Wang P F, Tian C L, Chen H W 2022 Acta Phys. Sin. 71 117601
Google Scholar
[31] 董杨, 杜博, 张少春, 陈向东, 孙方稳 2018 67 160301
Google Scholar
Dong Y, Du B, Zhang S C, Chen X D, Sun F W 2018 Acta Phys. Sin. 67 160301
Google Scholar
[32] 沈翔, 赵立业, 黄璞, 孔熙, 季鲁敏 2021 70 068501
Google Scholar
Shen X, Zhao L Y, Huang P, Kong X, Ji L M 2021 Acta Phys. Sin. 70 068501
Google Scholar
[33] Wu Y, Yang X X 2007 Appl. Phys. Lett. 91 094104
Google Scholar
[34] Liu J, Liu N, Shan C, Liu T, Li H, Zheng A, Xie X T 2016 Phys. Lett. A 380 2458
Google Scholar
[35] Dong X L, Li P B 2019 Phys. Rev. A 100 043825
Google Scholar
[36] Shou C, Huang G 2021 Front. Phys. 9 594680
Google Scholar
[37] Dong Y Y, Zheng X J, Wang D L, Ding J W 2021 Opt. Express 29 5367
Google Scholar
[38] Mu Y, Qin L, Shi Z Y, Huang G X 2021 Phys. Rev. A 103 043709
Google Scholar
[39] Xu Y B, Bai Z Y, Huang G X 2020 Phys. Rev. A 101 053859
Google Scholar
[40] Santori C, Fattal D, Spillane S M, Fiorentino M, Beausoleil R G, Greentree A D, Olivero P, Draganski M, Rabeau J R, Reichart P, Gibson B C, Rubanov S, Jamieson D N, Prawer S 2006 Opt. Express 14 7986
Google Scholar
[41] Liu D Q, Liu G Q, Chang Y C, Pan X Y 2014 Physica B 432 84
Google Scholar
[42] El-Ella H A R, Ahmadi S, Wojciechowski A M, Huck A, Andersen U L 2017 Opt. Express 25 14809
Google Scholar
[43] Ahmadi S, El-Ella H A R, Wojciechowski A M, Gehring T, Hansen J O B, Huck A, Andersen U L 2018 Phys. Rev. B 97 024105
Google Scholar
-
图 2 不同控制场磁感应强度${B_{\text{c}}}$下, 线性吸收特性${K_{{\text{0 i}}}}$随失谐量${\varDelta _{\text{p}}}$的变化情况. 图中参数为${\varGamma _{31}} = 0.35{\text{ MHz}}$, ${\varGamma _{21}} = 0.11{\text{ MHz}}$, $ {\gamma _{21}} = {\gamma _{31}} = 44{\text{ MHz}} $, ${\gamma _{32}} = 0.5{\text{ MHz}}$, ${\varDelta _{\text{c}}} = 1{\text{ MHz}}$, $ {k_{13}} = 2.3 \times {10^{10}}{\text{ cm}} \cdot {{\text{s}}^{ - 1}} $
Figure 2. Linear absorption coefficient ${K_{{\text{0 i}}}}$ as a function of the detuning ${\varDelta _{\text{p}}}$ with different magnetic induction strength ${B_{\text{c}}}$ of the control field. Parameters used are ${\varGamma _{31}} = 0.35{\text{ MHz}}$, ${\varGamma _{21}} = 0.11{\text{ MHz}}$, $ {\gamma _{21}} = {\gamma _{31}} = 44{\text{ MHz}} $, ${\gamma _{32}} = 0.5{\text{ MHz}}$, ${\varDelta _{\text{c}}} = 1{\text{ MHz}}$, $ {k_{13}} = 2.3 \times {10^{10}}{\text{ cm}} \cdot {{\text{s}}^{ - 1}} $.
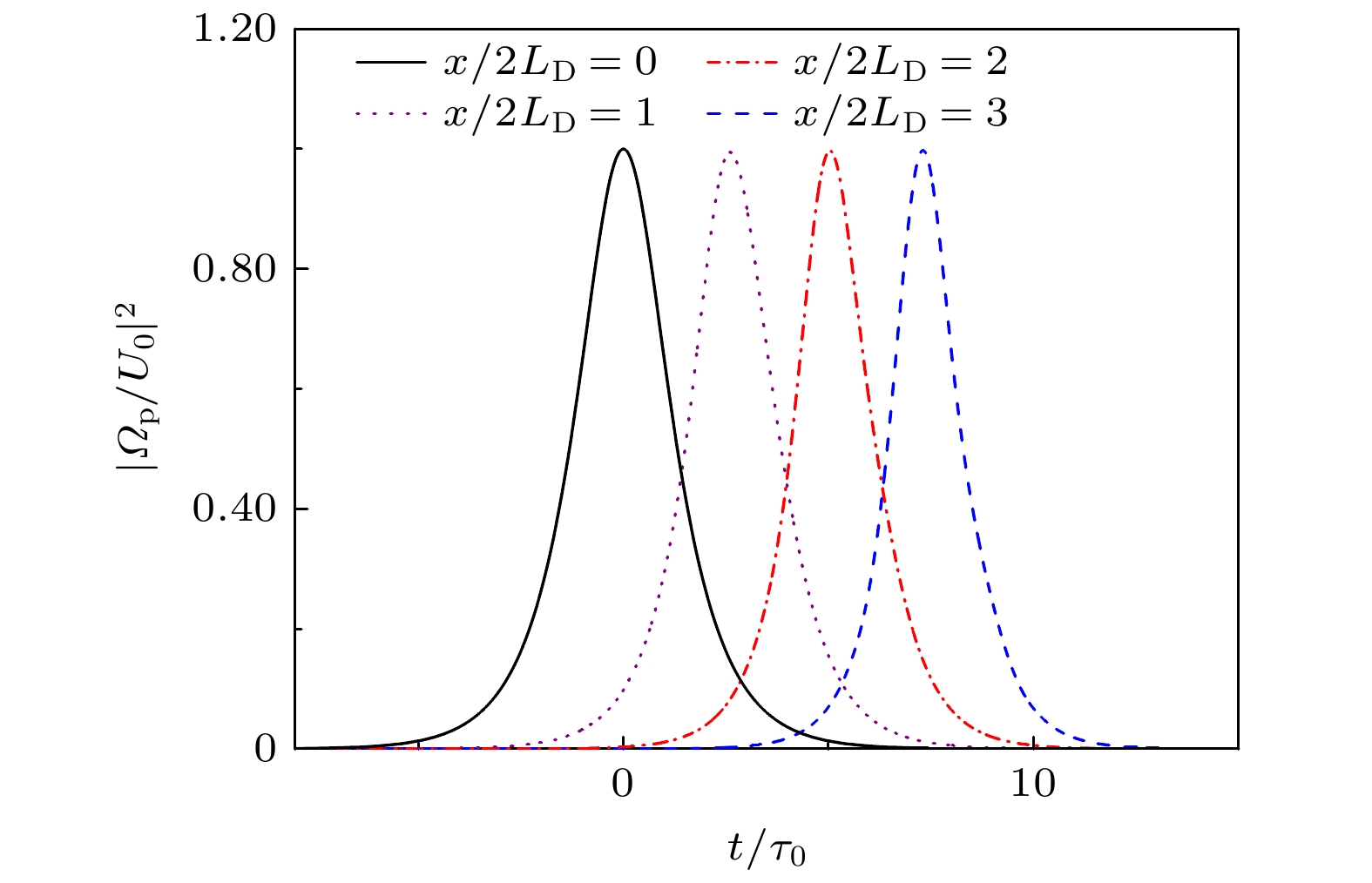
图 3 孤子的传播稳定性分析. 参数为$|{\varDelta _{\text{p}}}{\tau _0}| = 42.5$, $|{\varDelta _{\text{p}}}{\tau _0}| = 41.1$, $|{\varOmega _{\text{c}}}{\tau _0}| = 45$, ${\tau _0} = 7 \times {10^{ - 8}}\;{\text{s}}$, 其余参数与图2一致
Figure 3. Analysis of the propagation stability of solitons. Parameters used are $|{\varDelta _{\text{p}}}{\tau _0}| = 42.5$, $|{\varDelta _{\text{p}}}{\tau _0}| = 41.1$, $|{\varOmega _{\text{c}}}{\tau _0}| = $$ 45$, ${\tau _0} = 7 \times {10^{ - 8}}\;{\text{s}}$, other parameters used are the same as in Fig. 2.
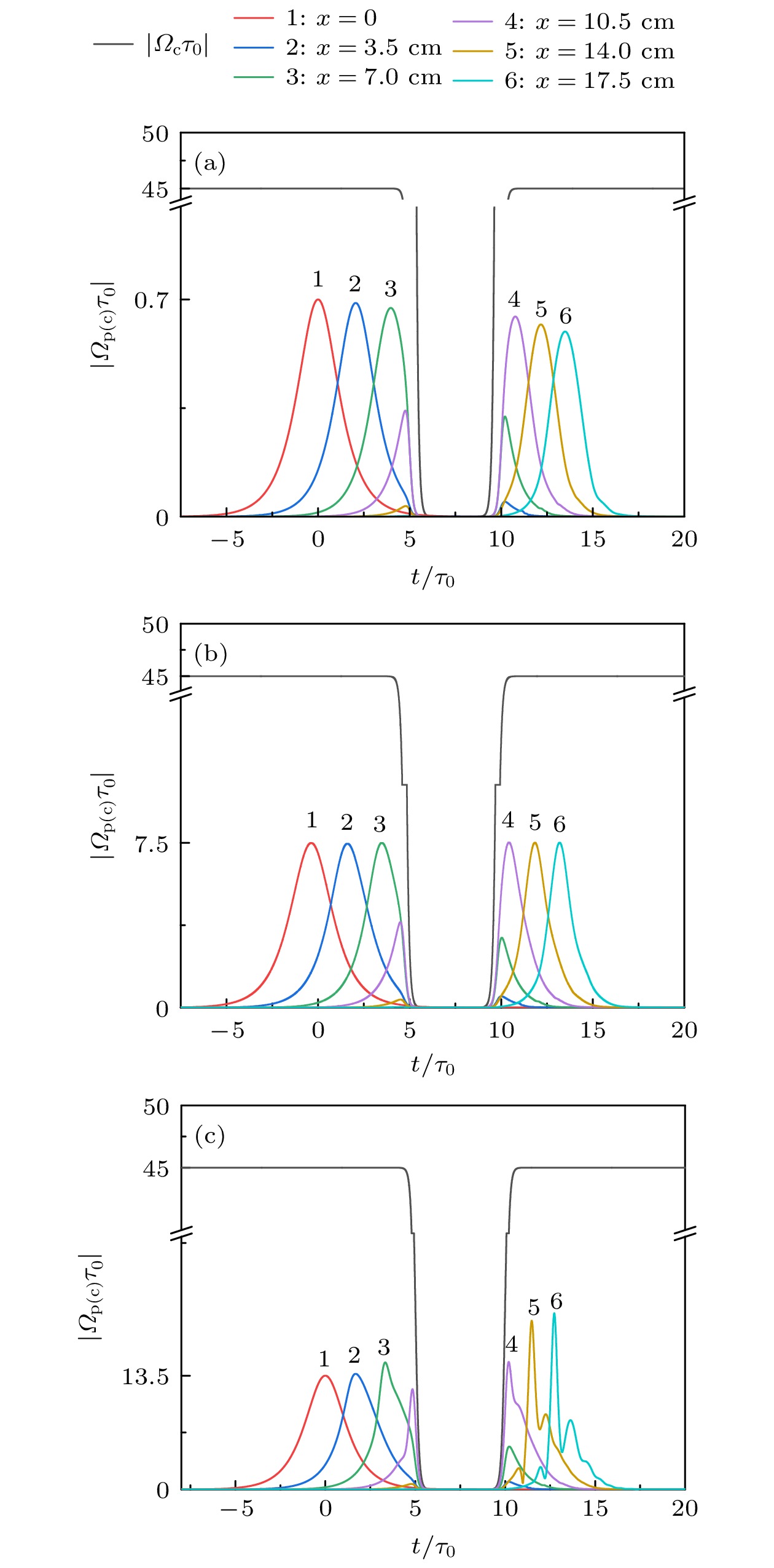
图 4 探测场的存储与读取 (a) 弱探测脉冲的存储与读取; (b) 孤子的存储与读取; (c)强探测脉冲的存储与读取. 图中使用的参数${T_{\text{s}}}/{\tau _0} = 0.2$, ${T_{{\text{on}}}}/{\tau _0} = 5$, ${T_{{\text{off}}}}/{\tau _0} = 10$, 其他参数与图3相同
Figure 4. Storage and retrieval of probe field: (a) Storage and retrieval of a weak probe pulse; (b) storage and retrieval of a soliton pulse; (c) storage and retrieval of a strong probe pulse. Parameters used are ${T_{\text{s}}}/{\tau _0} = 0.2$, ${T_{{\text{on}}}}/{\tau _0} = 5$, ${T_{{\text{off}}}}/{\tau _0} = 10$, other parameters used are the same as in Fig. 3.
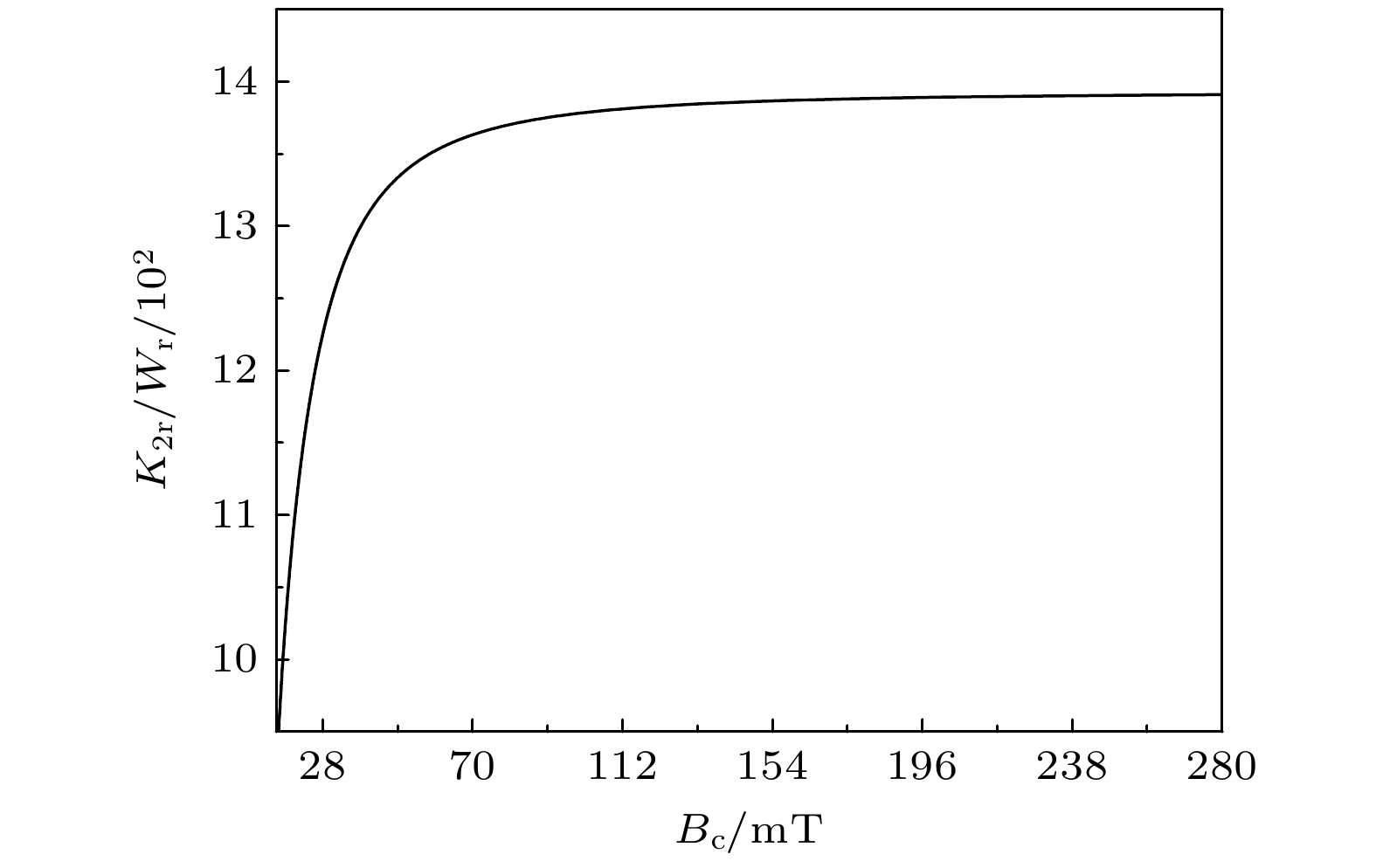
图 5 ${\varDelta _{\text{p}}} = 600$ MHz时, 存取孤子的振幅随控制场磁感应强度${B_{\text{c}}}$的变化. 其余参数与图2一致
Figure 5. Amplitude of the storgae and retrieval of soliton as a function of control fields magnetic induction strength ${B_{\text{c}}}$ at ${\varDelta _{\text{p}}} = 600$MHz. Other parameters used are the same as in Fig. 2.
-
[1] Haus H A, Wong W S 1996 Rev. Mod. Phys. 68 423
Google Scholar
[2] Wu Y, Deng L 2004 Phys. Rev. Lett. 93 143904
Google Scholar
[3] Huang G, Jiang K, Payne M G, Deng L 2006 Phys. Rev. E 73 056606
Google Scholar
[4] 任波, 佘彦超, 徐小凤, 叶伏秋 2021 70 224205
Google Scholar
Ren B, She Y C, Xu X F, Ye F Q 2021 Acta Phys. Sin. 70 224205
Google Scholar
[5] 高洁, 杭超 2022 71 133202
Google Scholar
Gao J, Hang C 2022 Acta Phys. Sin. 71 133202
Google Scholar
[6] Dong Y Y, Wang D L, Wang Y, Ding J W 2018 Phys. Lett. A 382 2006
Google Scholar
[7] Zhang X F, Yang Q, Zhang J F, Chen X Z, Liu W M 2008 Phys. Rev. A 77 023613
Google Scholar
[8] Wang Y, Ding J W, Wang D L 2020 Eur. Phys. J. D 74 190
Google Scholar
[9] Harris S E 1997 Phys. Today 50 36
[10] Fleischhauer M, Imamoglu A, Marangos J P 2005 Rev. Mod. Phys. 77 633
Google Scholar
[11] Huang G, Deng L, Payne M G 2005 Phys. Rev. E 72 016617
Google Scholar
[12] Hang C, Huang G X 2008 Phys. Rev. A 77 033830
Google Scholar
[13] Shou C, Huang G X 2019 Phys. Rev. A 99 043821
Google Scholar
[14] Bai Z Y, Hang C, Huang G X 2013 Chin. Opt. Lett. 11 012701
Google Scholar
[15] Chen Y, Bai Z Y, Huang G X 2014 Phys. Rev. A 89 023835
Google Scholar
[16] Wu Y, Yang X X 2005 Phys. Rev. A 71 053806
Google Scholar
[17] 王胤, 周驷杰, 陈桥, 邓永和 2023 72 084204
Google Scholar
Wang Y, Zhou S J, Chen Q, Deng Y H 2023 Acta Phys. Sin. 72 084204
Google Scholar
[18] Li P B, Xiang Z L, Rabl P, Nori F 2016 Phys. Rev. Lett. 117 015502
Google Scholar
[19] Doherty M W, Manson N B, Delaney P, Jelezko F, Wrachtrup J, Hollenberg L C L 2013 Phys. Rep. 528 1
Google Scholar
[20] Robledo L, Bernien H, Sar T V D, Hanson R 2011 New J. Phys. 13 025013
Google Scholar
[21] Yang W L, Yin Z Q, Hu Y, Feng M, Du J F 2011 Phys. Rev. A 84 010301
Google Scholar
[22] Lee D, Lee K W, Cady J V, Ovartchaiyapong P, Jayich A C B 2017 J. Opt. 19 033001
Google Scholar
[23] Ghaderi Goran Abad M, Mahmoudi M 2019 Eur. Phys. J. D 73 1
Google Scholar
[24] Yang X Y, Zhang N, Yuan H, Bian G D, Fan P C, Li M X 2019 AIP Adv. 9 075213
Google Scholar
[25] Lü X Y, Xiang Z L, Cui W, You J Q, Nori F 2013 Phys. Rev. A 88 012329
Google Scholar
[26] Grezes C, Julsgaard B, Kubo Y, Stern M, Umeda T, Isoya J, Sumiya H, Abe H, Onoda S, Ohshima T, Jacques V, Esteve J, Vion D, Esteve D, Mølmer K, Bertet P 2014 Phys. Rev. X 4 021049
[27] Dutt M V, Childress L, Jiang L, Togan E, Maze J, Jelezko F, Zibrov A S, Hemmer P R, Lukin M D 2007 Science 316 1312
Google Scholar
[28] Zhang M Q, Zheng A S, Chen Q L, Liu J B 2020 Optik 218 165255
Google Scholar
[29] Liu Y, Raza F, Li K, Ullah H, Zhang Y, Zhang W, Zhao W 2019 J. Opt. Soc. Am. B: Opt. Phys. 36 002727
[30] 吴建冬, 程智, 叶翔宇, 李兆凯, 王鹏飞, 田长麟, 陈宏伟 2022 71 117601
Google Scholar
Wu J D, Cheng Z, Ye X Y, Li Z K, Wang P F, Tian C L, Chen H W 2022 Acta Phys. Sin. 71 117601
Google Scholar
[31] 董杨, 杜博, 张少春, 陈向东, 孙方稳 2018 67 160301
Google Scholar
Dong Y, Du B, Zhang S C, Chen X D, Sun F W 2018 Acta Phys. Sin. 67 160301
Google Scholar
[32] 沈翔, 赵立业, 黄璞, 孔熙, 季鲁敏 2021 70 068501
Google Scholar
Shen X, Zhao L Y, Huang P, Kong X, Ji L M 2021 Acta Phys. Sin. 70 068501
Google Scholar
[33] Wu Y, Yang X X 2007 Appl. Phys. Lett. 91 094104
Google Scholar
[34] Liu J, Liu N, Shan C, Liu T, Li H, Zheng A, Xie X T 2016 Phys. Lett. A 380 2458
Google Scholar
[35] Dong X L, Li P B 2019 Phys. Rev. A 100 043825
Google Scholar
[36] Shou C, Huang G 2021 Front. Phys. 9 594680
Google Scholar
[37] Dong Y Y, Zheng X J, Wang D L, Ding J W 2021 Opt. Express 29 5367
Google Scholar
[38] Mu Y, Qin L, Shi Z Y, Huang G X 2021 Phys. Rev. A 103 043709
Google Scholar
[39] Xu Y B, Bai Z Y, Huang G X 2020 Phys. Rev. A 101 053859
Google Scholar
[40] Santori C, Fattal D, Spillane S M, Fiorentino M, Beausoleil R G, Greentree A D, Olivero P, Draganski M, Rabeau J R, Reichart P, Gibson B C, Rubanov S, Jamieson D N, Prawer S 2006 Opt. Express 14 7986
Google Scholar
[41] Liu D Q, Liu G Q, Chang Y C, Pan X Y 2014 Physica B 432 84
Google Scholar
[42] El-Ella H A R, Ahmadi S, Wojciechowski A M, Huck A, Andersen U L 2017 Opt. Express 25 14809
Google Scholar
[43] Ahmadi S, El-Ella H A R, Wojciechowski A M, Gehring T, Hansen J O B, Huck A, Andersen U L 2018 Phys. Rev. B 97 024105
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 1403
- PDF Downloads: 55
- Cited By: 0
