-
Gaussian boson sampling is one of the main promising approaches to realizing the quantum computational advantage, which also offers potential applications such as in dense subgraphs problem and quantum chemistry. However, the inevitable noise in experiment may weaken the quantum advantage of Gaussian boson sampling. Photon loss and photon partial indistinguishability are two major sources of noise. Their influence on the complexity of Gaussian boson sampling has been extensively studied in previous work. However, the phase noise of the input light source, a noise which is suitable for tailored for Gaussian boson sampling, has not been studied so far. Here, we investigate the phase noise of the input light source in Gaussian boson sampling through numerical simulation. We use the Monte Carlo method to calculate the output probability distribution under phase noise approximately. It is found that the phase noise of the light source can cause the input state to change from a Gaussian state into a non-Gaussian mixed state. For a given phase noise level, the fidelity of the non-Gaussian mixed state and the noise-free ideal state decreases monotonically as the mean photon number of input increases. Meanwhile, owing to the phase noise the deviation of the output probability distribution gradually increases with the number of detected photons increasing. Furthermore, the phase noise results in the capability of heavy sample generation (HOG), significantly decreasing. Finally, it is found that Gaussian boson sampling with photon loss is more tolerant to phase noise than the lossless case given that the mean photon number of input is the same. Our study is helpful in suppressing the phase noise in large-scale Gaussian boson sampling experiments.
[1] Harrow A W, Montanaro A 2017 Nature 549 203
Google Scholar
[2] Aaronson S, Arkhipov A 2011 Proceedings of the Forty-third Annual ACM Symposium on Theory of Computing New York, USA, June 6, 2011 p333
[3] Broome M A, Fedrizzi A, Rahimi-Keshari S, Dove J, Aaronson S, Ralph T C, White A G 2013 Science 339 794
Google Scholar
[4] Spring J B, Metcalf B J, Humphreys P C, Kolthammer W S, Jin X M, Barbieri M, Datta A, Thomas-Peter N, Langford N K, Kundys D, Gates J C, Smith B J, Smith P G R, Walmsley I A 2013 Science 339 798
Google Scholar
[5] Crespi A, Osellame R, Ramponi R, Brod D J, Galvão E F, Spagnolo N, Vitelli C, Maiorino E, Mataloni P, Sciarrino F 2013 Nat. Photonics 7 545
Google Scholar
[6] Wang H, He Y, Li Y H, Su Z E, Li B, Huang H L, Ding X, Chen M C, Liu C, Qin J, Li J P, He Y M, Schneider C, Kamp M, Peng C Z, Höfling S, Lu C Y, Pan J W 2017 Nat. Photonics 11 361
Google Scholar
[7] He Y, Ding X, Su Z E, Huang H L, Qin J, Wang C, Unsleber S, Chen C, Wang H, He Y M, Wang X L, Zhang W J, Chen S J, Schneider C, Kamp M, You L X, Wang Z, Höfling S, Lu C Y, Pan J W 2017 Phys. Rev. Lett. 118 190501
Google Scholar
[8] Wang H, Li W, Jiang X, He Y M, Li Y H, Ding X, Chen M C, Qin J, Peng C Z, Schneider C, Kamp M, Zhang W J, Li H, You L X, Wang Z, Dowling J P, Höfling S, Lu C Y, Pan J W 2018 Phys. Rev. Lett. 120 230502
Google Scholar
[9] Zhong H S, Peng L C, Li Y, Hu Y, Li W, Qin J, Wu D, Zhang W, Li H, Zhang L, Wang Z, You L, Jiang X, Li L, Liu N L, Dowling J P, Lu C Y, Pan J W 2019 Sci. Bull. 64 511
Google Scholar
[10] Wang H, Qin J, Ding X, Chen M C, Chen S, You X, He Y M, Jiang X, You L, Wang Z, Schneider C, Renema J J, Höfling S, Lu C Y, Pan J W 2019 Phys. Rev. Lett. 123 250503
Google Scholar
[11] Walschaers M, Kuipers J, Urbina J D, Mayer K, Tichy M C, Richter K, Buchleitner A 2016 New J. Phys. 18 032001
Google Scholar
[12] Spagnolo N, Vitelli C, Bentivegna M, Brod D J, Crespi A, Flamini F, Giacomini S, Milani G, Ramponi R, Mataloni P, Osellame R, Galvão E F, Sciarrino F 2014 Nat. Photonics 8 615
Google Scholar
[13] Aaronson S, Brod D J 2016 Phys. Rev. A 93 012335
Google Scholar
[14] Renema J J, Menssen A, Clements W R, Triginer G, Kolthammer W S, Walmsley I A 2018 Phys. Rev. Lett. 120 220502
Google Scholar
[15] Shchesnovich V S 2019 Phys. Rev. A 100 012340
Google Scholar
[16] Qi H, Brod D J, Quesada N, García-Patrón R 2020 Phys. Rev. Lett. 124 100502
Google Scholar
[17] Lund A P, Laing A, Rahimi-Keshari S, Rudolph T, O’Brien J L, Ralph T C 2014 Phys. Rev. Lett. 113 100502
Google Scholar
[18] Hamilton C S, Kruse R, Sansoni L, Barkhofen S, Silberhorn C, Jex I 2017 Phys. Rev. Lett. 119 170501
Google Scholar
[19] Deshpande A, Mehta A, Vincent T, Quesada N, Hinsche M, Ioannou M, Madsen L, Lavoie J, Qi H, Eisert J, Hangleiter D, Fefferman B, Dhand I 2022 Sci. Adv. 8 eabi7894
Google Scholar
[20] Zhong H S, Wang H, Deng Y H, Chen M C, Peng L C, Luo Y H, Qin J, Wu D, Ding X, Hu Y, Hu P, Yang X Y, Zhang W J, Li H, Li Y, Jiang X, Gan L, Yang G, You L, Wang Z, Li L, Liu N L, Lu C Y, Pan J W 2020 Science 370 1460
Google Scholar
[21] Zhong H S, Deng Y H, Qin J, Wang H, Chen M C, Peng L C, Luo Y H, Wu D, Gong S Q, Su H, Hu Y, Hu P, Yang X Y, Zhang W J, Li H, Li Y, Jiang X, Gan L, Yang G, You L, Wang Z, Li L, Liu N L, Renema J J, Lu C Y, Pan J W 2021 Phys. Rev. Lett. 127 180502
Google Scholar
[22] Madsen L S, Laudenbach F, Askarani M Falamarzi, Rortais F, Vincent T, Bulmer J F F, Miatto F M, Neuhaus L, Helt L G, Collins M J, Lita A E, Gerrits T, Nam S W, Vaidya V D, Menotti M, Dhand I, Vernon Z, Quesada N, Lavoie J 2022 Nature 606 75
Google Scholar
[23] Bulmer J F F, Bell B A, Chadwick R S, Jones A E, Moise D, Rigazzi A, Thorbecke J, Haus U U, Van Vaerenbergh T, Patel R B, Walmsley I A, Laing A 2022 Sci. Adv. 8 eabl9236
Google Scholar
[24] Oh C, Lim Y, Fefferman B, Jiang L 2022 Phys. Rev. Lett. 128 190501
Google Scholar
[25] Mandel L 1986 Phys. Scr. 1986 34
Google Scholar
[26] Campos R A, Saleh B E, Teich M C 1989 Phys. Rev. A 40 1371
Google Scholar
[27] Arrazola J M, Bromley T R 2018 Phys. Rev. Lett. 121 030503
Google Scholar
[28] Banchi L, Fingerhuth M, Babej T, Ing C, Arrazola J M 2020 Sci. Adv. 6 eaax1950
Google Scholar
-
图 1 不同相位噪声下单模压缩真空态的Wigner函数
Figure 1. Wigner function of single-mode squeezed vacuum state under different phase noise
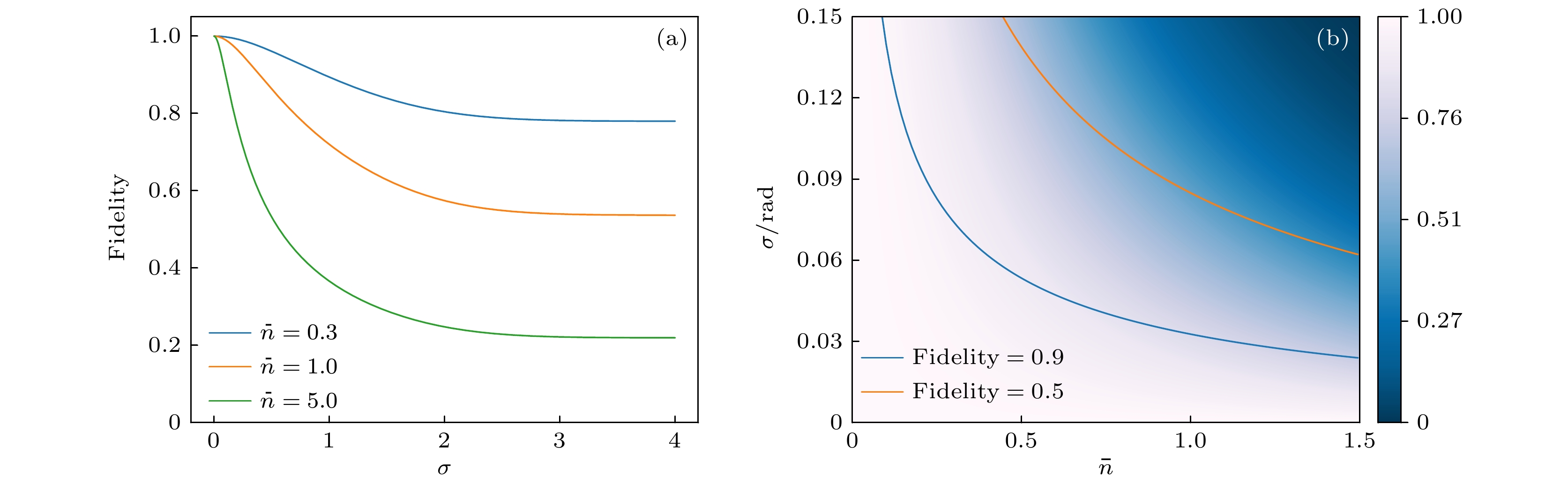
图 2 相位噪声压缩态和理想态的保真度 (a)不同单模平均光子数
$ \bar{n} $ 下保真度随噪声大小σ的变化; (b)输入压缩态个数$ K = 100 $ 时, 总保真度随$ \bar{n} $ 和σ的变化Figure 2. Fidelity between squeezed state under phase noise and the ideal state: (a) Fidelity as a function of phase noise level σ under different single-mode mean photon number
$ \bar{n} $ ; (b) when the number of input squeezed states is$ K = 100 $ , the total fidelity as a function of$ \bar{n} $ and σ.
图 3 相位噪声对输出概率分布的影响 (a)不同相位噪声下, 噪声输出分布和理想分布的海林格距离随探测光子数的变化, 图中每个点代表10个随机干涉网络结果的均值; (b)光子数
$ k = 8 $ 时, 典型的相位噪声下样本概率和理想样本概率(蓝色曲线)的相对误差的对数曲线(浅红色), 红色曲线为浅红色曲线的步长为15的移动平均值, 相位噪声$ \sigma = 0.8 $ ; (c)$ \Delta {\rm HOG} $ 随相位噪声大小的变化; 图(a)—(c)采用的参数为输入压缩态个数$ K = 5 $ , 单模平均光子数$ \bar{n} = 1 $ , 模式数$ m = 9 $ Figure 3. Effect of phase noise on output probability distribution: (a) Hellinger distance of phase noisy distribution and ideal distribution as a function of total detected photon number k under different noise level, each point is the mean result of 10 random choosed interferometer; (b) logarithmic curve (light red) of relative error of noisy sample probability and ideal sample probability (blue curve), the red curve is the 15-point moving mean of light red curve, phase noise
$ \sigma = 0.8 $ ; (c)$ \Delta {\rm HOG} $ as a function of phase noise. In panels (a)−(c), the number of input squeezed states is$ K = 5 $ , the single-mode mean photon number is$ \bar{n} = 1 $ , the mode number is$ m = 9 $ 
图 4 光子损失的影响, 保持输入平均光子数
$ \bar{n} = 1 $ 不变 (a)不同光子损耗η下保真度和相位噪声大小的关系; (b)在相位噪声$ \sigma = 0.8 $ 时, 比较有光子损失$ \eta = 0.7 $ 情形(蓝色点)和无光子损失(红色点)下噪声分布和理想分布的海林格距离, 可以看出有损耗时海林格距离显著降低了Figure 4. The effect of photon loss. Keeping the mean photon number
$ \bar{n} = 1 $ unchanged: (a) Relationship between fidelity and phase noise under different photon losses; (b) for$ \sigma = 0.8 $ , comparing the Hellinger distance of phase noisy distribution and the ideal distribution with photon loss$ \eta = 0.7 $ (blue point) and without photon loss (red point). The Hellinger distance is significantly lower with the photon loss case -
[1] Harrow A W, Montanaro A 2017 Nature 549 203
Google Scholar
[2] Aaronson S, Arkhipov A 2011 Proceedings of the Forty-third Annual ACM Symposium on Theory of Computing New York, USA, June 6, 2011 p333
[3] Broome M A, Fedrizzi A, Rahimi-Keshari S, Dove J, Aaronson S, Ralph T C, White A G 2013 Science 339 794
Google Scholar
[4] Spring J B, Metcalf B J, Humphreys P C, Kolthammer W S, Jin X M, Barbieri M, Datta A, Thomas-Peter N, Langford N K, Kundys D, Gates J C, Smith B J, Smith P G R, Walmsley I A 2013 Science 339 798
Google Scholar
[5] Crespi A, Osellame R, Ramponi R, Brod D J, Galvão E F, Spagnolo N, Vitelli C, Maiorino E, Mataloni P, Sciarrino F 2013 Nat. Photonics 7 545
Google Scholar
[6] Wang H, He Y, Li Y H, Su Z E, Li B, Huang H L, Ding X, Chen M C, Liu C, Qin J, Li J P, He Y M, Schneider C, Kamp M, Peng C Z, Höfling S, Lu C Y, Pan J W 2017 Nat. Photonics 11 361
Google Scholar
[7] He Y, Ding X, Su Z E, Huang H L, Qin J, Wang C, Unsleber S, Chen C, Wang H, He Y M, Wang X L, Zhang W J, Chen S J, Schneider C, Kamp M, You L X, Wang Z, Höfling S, Lu C Y, Pan J W 2017 Phys. Rev. Lett. 118 190501
Google Scholar
[8] Wang H, Li W, Jiang X, He Y M, Li Y H, Ding X, Chen M C, Qin J, Peng C Z, Schneider C, Kamp M, Zhang W J, Li H, You L X, Wang Z, Dowling J P, Höfling S, Lu C Y, Pan J W 2018 Phys. Rev. Lett. 120 230502
Google Scholar
[9] Zhong H S, Peng L C, Li Y, Hu Y, Li W, Qin J, Wu D, Zhang W, Li H, Zhang L, Wang Z, You L, Jiang X, Li L, Liu N L, Dowling J P, Lu C Y, Pan J W 2019 Sci. Bull. 64 511
Google Scholar
[10] Wang H, Qin J, Ding X, Chen M C, Chen S, You X, He Y M, Jiang X, You L, Wang Z, Schneider C, Renema J J, Höfling S, Lu C Y, Pan J W 2019 Phys. Rev. Lett. 123 250503
Google Scholar
[11] Walschaers M, Kuipers J, Urbina J D, Mayer K, Tichy M C, Richter K, Buchleitner A 2016 New J. Phys. 18 032001
Google Scholar
[12] Spagnolo N, Vitelli C, Bentivegna M, Brod D J, Crespi A, Flamini F, Giacomini S, Milani G, Ramponi R, Mataloni P, Osellame R, Galvão E F, Sciarrino F 2014 Nat. Photonics 8 615
Google Scholar
[13] Aaronson S, Brod D J 2016 Phys. Rev. A 93 012335
Google Scholar
[14] Renema J J, Menssen A, Clements W R, Triginer G, Kolthammer W S, Walmsley I A 2018 Phys. Rev. Lett. 120 220502
Google Scholar
[15] Shchesnovich V S 2019 Phys. Rev. A 100 012340
Google Scholar
[16] Qi H, Brod D J, Quesada N, García-Patrón R 2020 Phys. Rev. Lett. 124 100502
Google Scholar
[17] Lund A P, Laing A, Rahimi-Keshari S, Rudolph T, O’Brien J L, Ralph T C 2014 Phys. Rev. Lett. 113 100502
Google Scholar
[18] Hamilton C S, Kruse R, Sansoni L, Barkhofen S, Silberhorn C, Jex I 2017 Phys. Rev. Lett. 119 170501
Google Scholar
[19] Deshpande A, Mehta A, Vincent T, Quesada N, Hinsche M, Ioannou M, Madsen L, Lavoie J, Qi H, Eisert J, Hangleiter D, Fefferman B, Dhand I 2022 Sci. Adv. 8 eabi7894
Google Scholar
[20] Zhong H S, Wang H, Deng Y H, Chen M C, Peng L C, Luo Y H, Qin J, Wu D, Ding X, Hu Y, Hu P, Yang X Y, Zhang W J, Li H, Li Y, Jiang X, Gan L, Yang G, You L, Wang Z, Li L, Liu N L, Lu C Y, Pan J W 2020 Science 370 1460
Google Scholar
[21] Zhong H S, Deng Y H, Qin J, Wang H, Chen M C, Peng L C, Luo Y H, Wu D, Gong S Q, Su H, Hu Y, Hu P, Yang X Y, Zhang W J, Li H, Li Y, Jiang X, Gan L, Yang G, You L, Wang Z, Li L, Liu N L, Renema J J, Lu C Y, Pan J W 2021 Phys. Rev. Lett. 127 180502
Google Scholar
[22] Madsen L S, Laudenbach F, Askarani M Falamarzi, Rortais F, Vincent T, Bulmer J F F, Miatto F M, Neuhaus L, Helt L G, Collins M J, Lita A E, Gerrits T, Nam S W, Vaidya V D, Menotti M, Dhand I, Vernon Z, Quesada N, Lavoie J 2022 Nature 606 75
Google Scholar
[23] Bulmer J F F, Bell B A, Chadwick R S, Jones A E, Moise D, Rigazzi A, Thorbecke J, Haus U U, Van Vaerenbergh T, Patel R B, Walmsley I A, Laing A 2022 Sci. Adv. 8 eabl9236
Google Scholar
[24] Oh C, Lim Y, Fefferman B, Jiang L 2022 Phys. Rev. Lett. 128 190501
Google Scholar
[25] Mandel L 1986 Phys. Scr. 1986 34
Google Scholar
[26] Campos R A, Saleh B E, Teich M C 1989 Phys. Rev. A 40 1371
Google Scholar
[27] Arrazola J M, Bromley T R 2018 Phys. Rev. Lett. 121 030503
Google Scholar
[28] Banchi L, Fingerhuth M, Babej T, Ing C, Arrazola J M 2020 Sci. Adv. 6 eaax1950
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 3838
- PDF Downloads: 100
- Cited By: 0
