-
Like internet, connecting quantum computers together to build a full quantum network will enhance the ability to process quantum information. On-chip quantum memories can possess the essential functionalities in building a quantum network, including synchronizing a large number of quantum computers and implementing long-distance quantum communication. However, owning mainly to the constraints imposed by the micro-photonic structures themselves, on-chip quantum memories cannot satisfy the requirement for constructing the full quantum network for the incompatibility of their memory property and integration property. We here propose to build an on-chip quantum memory by using spatial-phase-mismatching effect in photonic crystal cavities. In this scenario, not only is the large orbital angular momentum of photonic crystal cavities utilized to realize photon-echo type memory, but also the light-matter enhancement of a photonic cavity is used to achieve a high-efficiency quantum storage.
-
Keywords:
- quantum memory /
- photon echo /
- photonic crystal cavity /
- spatial-phase-mismatching
[1] Lvovsky A I, Sanders B C, Tittel W 2009 Nat. Photonics 3 706
Google Scholar
[2] Sangouard N, Simon C, Riedmatten H D, Gisin N 2011 Rev. Mod. Phys. 83 33
Google Scholar
[3] Heshami K, England D G, Humphreys P C, Bustard P J, Acosta V M, Nunn J, Sussman B J 2016 J. Mod. Opt. 63 2005
Google Scholar
[4] Simon C 2017 Nat. Photonics 11 678
Google Scholar
[5] Kimble H J 2008 Nature 453 1023
Google Scholar
[6] Bussieres F, Sangouard N, Afzelius M, Riedmatten H D, Tittel W 2013 J. Mod. Opt. 60 1519
Google Scholar
[7] Saglamyurek E, Sinclair N, Jin J, Slater J A, Oblak D, Bussieres F, George M, Ricken R, Sohler W, Tittel W 2011 Nature 469 512
Google Scholar
[8] Liu C, Zhu T X, Su M X, Ma Y Z, Zhou Z Q, Li C F, Guo G C 2020 Phys. Rev. Lett. 125 260504
Google Scholar
[9] Liu C, Zhou Z Q, Zhu T X, Zheng L, Jin M, Liu X, Li P Y, Huang J Y, Ma Y, Tu T, Yang T S, Li C F, Guo G C 2020 Optica 7 192
[10] Zhong T, Kindem J M, Bartholomew J G, Rochman J, Craiciu I, Miyazono E, Bettinelli M, Cavalli E, Verma V, Nam S W, Marsili F, Shaw M D, Beyer A D, Faraon A 2017 Science 357 1392
Google Scholar
[11] Craiciu I, Lei M, Rochman J, Bartholomew J G, Faraon A 2021 Optica 8 114
[12] Hétet G, Longdell J J, Alexander A L, Lam P K, Sellars M J 2008 Phys. Rev. Lett. 100 23601
Google Scholar
[13] Moiseev S A, Kröll S 2001 Phys. Rev. Lett. 87 173601
[14] Kraus B, Tittel W, Gisin N, Nilsson M, Kröll S, Cirac J I Phys. Rev. A 73 020302
[15] Alexander A L, Longdell J J, Sellars M J, Manson N B 2006 Phys. Rev. Lett. 96 043602
Google Scholar
[16] Riedmatten H D, AfZelius M, Staudt M U, Simon C, Gisin N 2008 Nature 456 07607
[17] Mcauslan D L, Ledingham P M, Naylor W R, Beavan S E, Longdell J J 2011 Phys. Rev. A 84 022309
Google Scholar
[18] Afzelius M, Simon C, Riedmatten H De, Gisin N 2009 Phys. Rev. A 79 052329
Google Scholar
[19] Chanelière T, Hétet G 2015 Opt. Lett. 40 1294
Google Scholar
[20] McDonald H C 2016 Ph. D. Dissertation (Otago: University of Otago)
[21] Ma Y Z, Jin M, Chen D L, Zhou Z Q, Li C F, Guo G C 2021 Nat. Commun. 12 4378
Google Scholar
[22] Damon V, Bonarota M, Louchet-Chauvet A, Chaneliere T, Le Gouët J L 2011 New J. Phys. 13 093031
Google Scholar
[23] Dajczgewand J, Le Gouët J L, Louchet-Chauvet A, Chanelière T 2014 Opt. Lett. 39 2711
Google Scholar
[24] Fu Y, Wang M F, Zheng Y Z 2014 Opt. Commun. 321 162
Google Scholar
[25] Fan S, Villeneuve P R, Joannopoulos J D, Haus H A 1998 Opt. Express 3 4
[26] Afzelius1 M, Simon C 2010 Phys. Rev. A 82 022310
[27] Wang J, Sciarrino F, Laing A, Thompson M G 2020 Nat. Photonics 14 273
Google Scholar
[28] Zhong T, Goldner P 2019 Nanophotonics 8 2003
Google Scholar
[29] Hughes M A, Panjwani N A, Urdampilleta M, Homewood K P, Murdin B, Carey J D 2021 Appl. Phys. Lett. 118 194001
Google Scholar
[30] Yin C, Rancic M, Boo G G, Stavrias N, McCallum J C, Sellars M J, Rogge S 2013 Nature 497 91
Google Scholar
-
图 1 双
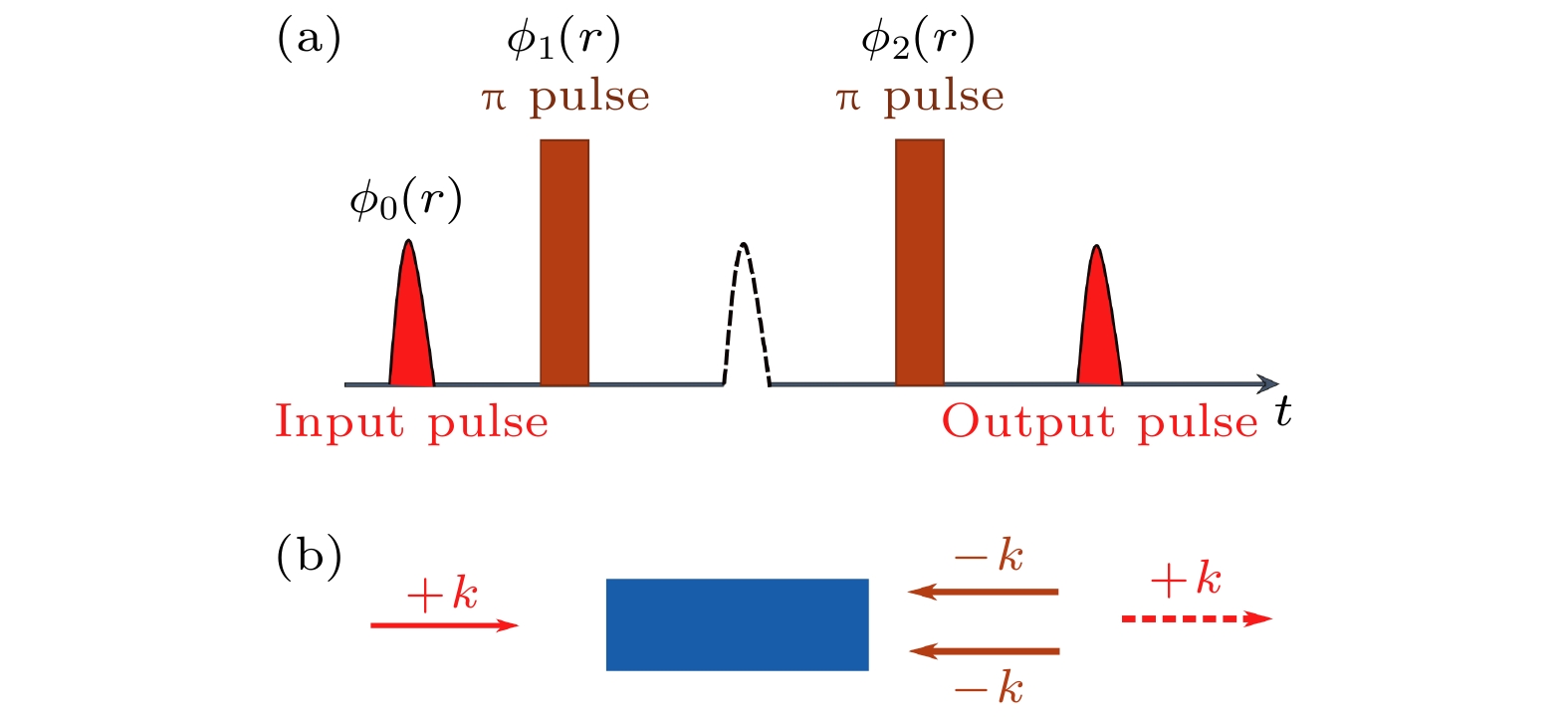
$ \pi $ 脉冲作用下的光子回波静默和再现操作 (a)双$ \pi $ 脉冲光子回波技术的脉冲序列, 输入信号光的空间相位分布为$ \phi_0(r) $ , 第一个$ \pi $ 脉冲对应的空间相位分布为$ \phi_1(r) $ , 并且$ \phi_1(r) \neq \phi_0(r) $ , 第二个$ \pi $ 脉冲对应的空间相位分布为$ \phi_2(r) $ ; (b)在自由空间的ROSE存储技术中,$ \phi_1(r) \neq \phi_0(r) $ 可通过控制脉冲光和控制脉冲的入射方向来实现. 例如, 图中的信号脉冲从左侧入射$ \phi_0 = {\rm{i}} k r $ ,$ \pi $ 脉冲从右侧入射$ \phi_1 = \phi_2 = -{\rm{ i }}k r $ Figure 1. The silence and revival of two-
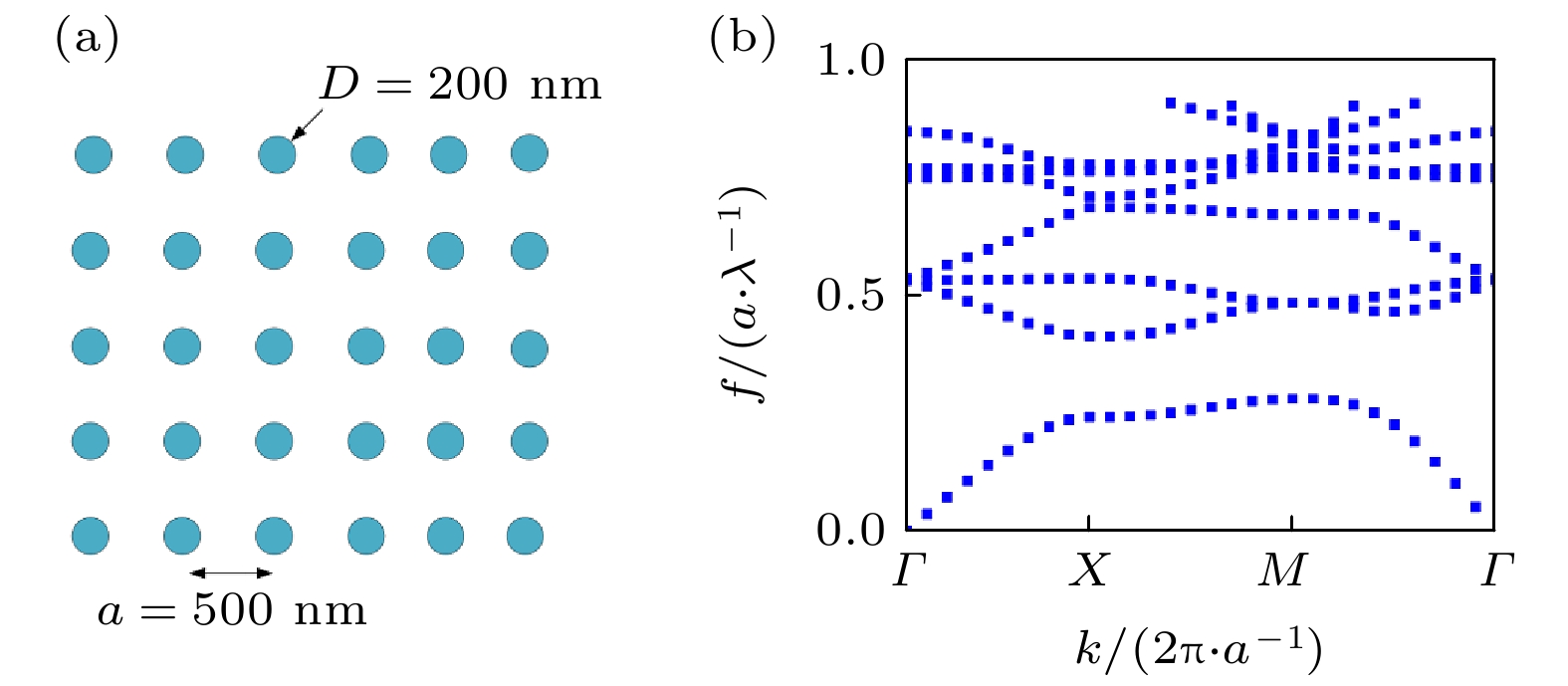
$ \pi $ -pulse photon echo: (a) Pulse sequence of two-$ \pi $ -pulse photon echo. The phase distribution of the input pulse is$ \phi_0(r) $ , that of the first$ \pi $ pulse is$ \phi_1(r) $ , where$ \phi_1(r) \neq \phi_0(r) $ , and that of the second$ \pi $ pulse is$ \phi_2(r) $ . (b) In free space ROSE,$ \phi_1(r) $ differs from$ \phi_0(r) $ due to the different propagating directions of the signal pluse and the$ \pi $ pulses. In panel (b), the signal pulse incoming from the left has$ \phi_0 = {\rm{i}} k r $ , and the$ \pi $ pulses incoming from the right have$ \phi_1 = \phi_2 = -{\rm{ i}} k r $ .
图 2 拟采用的光子晶体结构 (a)光子晶体结构, 光子晶体为正方晶格结构, 周期为500 nm, 其中蓝色柱子为掺铒的硅材料, 直径
$ D = 200 $ nm; (b)计算得到的光子晶体能带图, 带隙在$1.21 — 1.78\;\text{µ} {\rm{m}}$ 范围内Figure 2. Photonic crystal: (a) Structurre of the photonic crystal. The photonic crystal has a square lattice, whose period is 500 nm. The circles stands for the silicon pillars with a diameter of
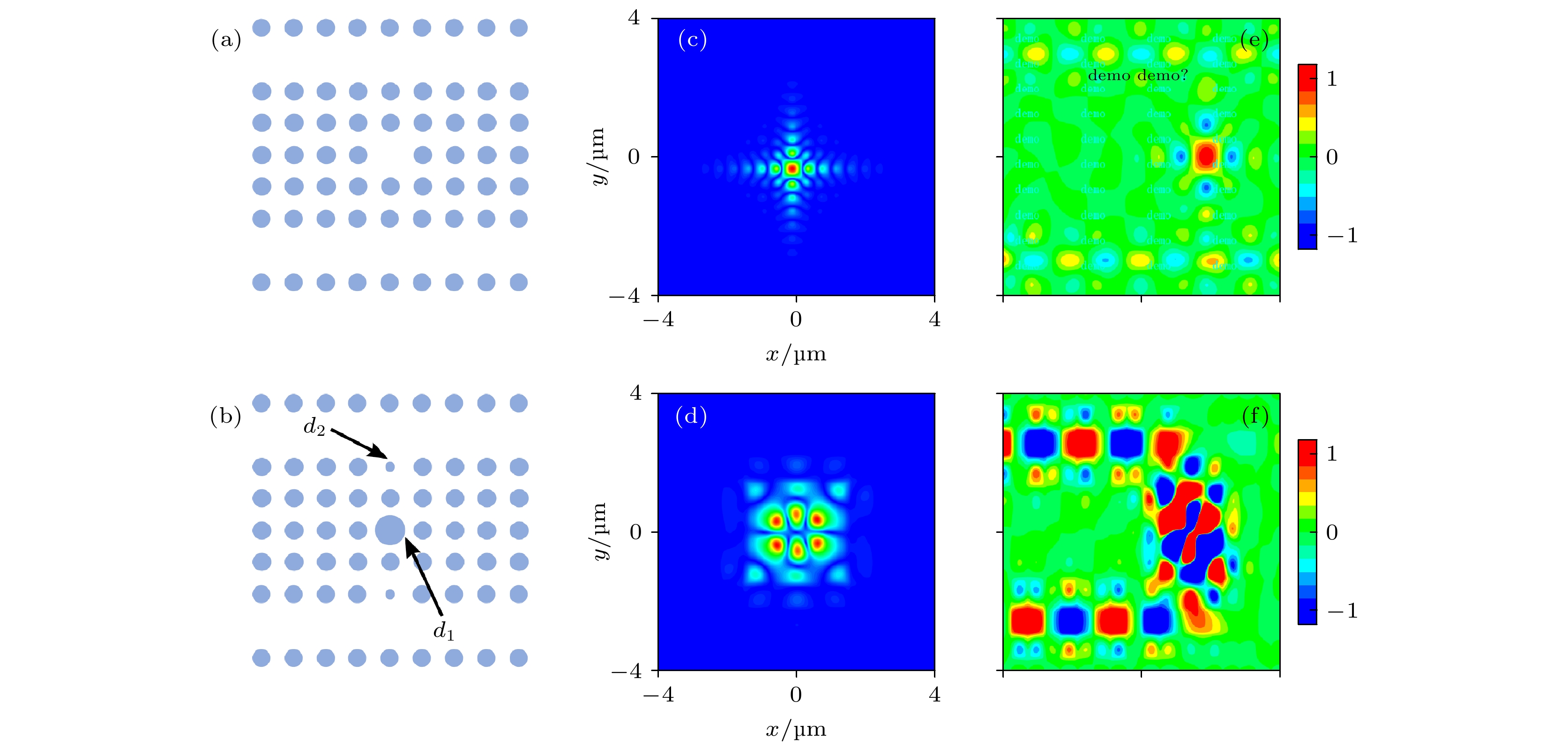
$ D = 200 $ nm. (b) Energy band of the photonic crystal in panel (a), showing a bandgap within 1.21–1.78$\;\text{µ} {\rm{m}}$ 
图 3 两种不同的光子晶体微腔. 单极子谐振模式 (a)在光子晶体中去掉一个硅柱子可以形成一个缺陷态微腔. 这样一种腔支持单极子的谐振模式, 如图(c)所示. 入射光从左上方的光子晶体波导入射耦合到光子晶体腔中, 如图(e)所示. 由于单极子谐振模式是一种类似于驻波的谐振模式, 因此无法通过调节阻抗匹配实现100%的单端输出. 六极子谐振模式: (b)把光子晶体中间的硅柱子直径增加为
$ d_1 = 700 $ nm, 并且将边沿的一个硅柱子直径减小为$ d_2 = 150 $ nm, 可以形成另一种光学微腔. 这样一种光学腔支持六极子的谐振模式, 其场分布如图(d)所示. 当入射光同样从左上方的光子晶体波导耦合到光子晶体腔时, 如图(f)所示, 六单极子谐振模式类似于一个顺时针旋转的回音壁模式, 可以通过调节阻抗匹配实现能量接近100%地从左下角的端口输出Figure 3. Two photonic-crystal cavities. Monopole resonace: (a) Removing a rod in the photonic crystal forms a defect cavity. One of the resonances of the structure (a) is a monopole resonance, the field distribution of which is shown in panel (c). Such a monopole mode is analogous to standing-wave resonance, and has a constant phase in space. This means that single-port output to one end of the waveguides can not be realized bu tuning the waveguide-cavity coupling, as shown in panel (e). Hexapole resonance: (b) By increasing the diameter of the central rod to 700 nm and reducing the rods at the edge to
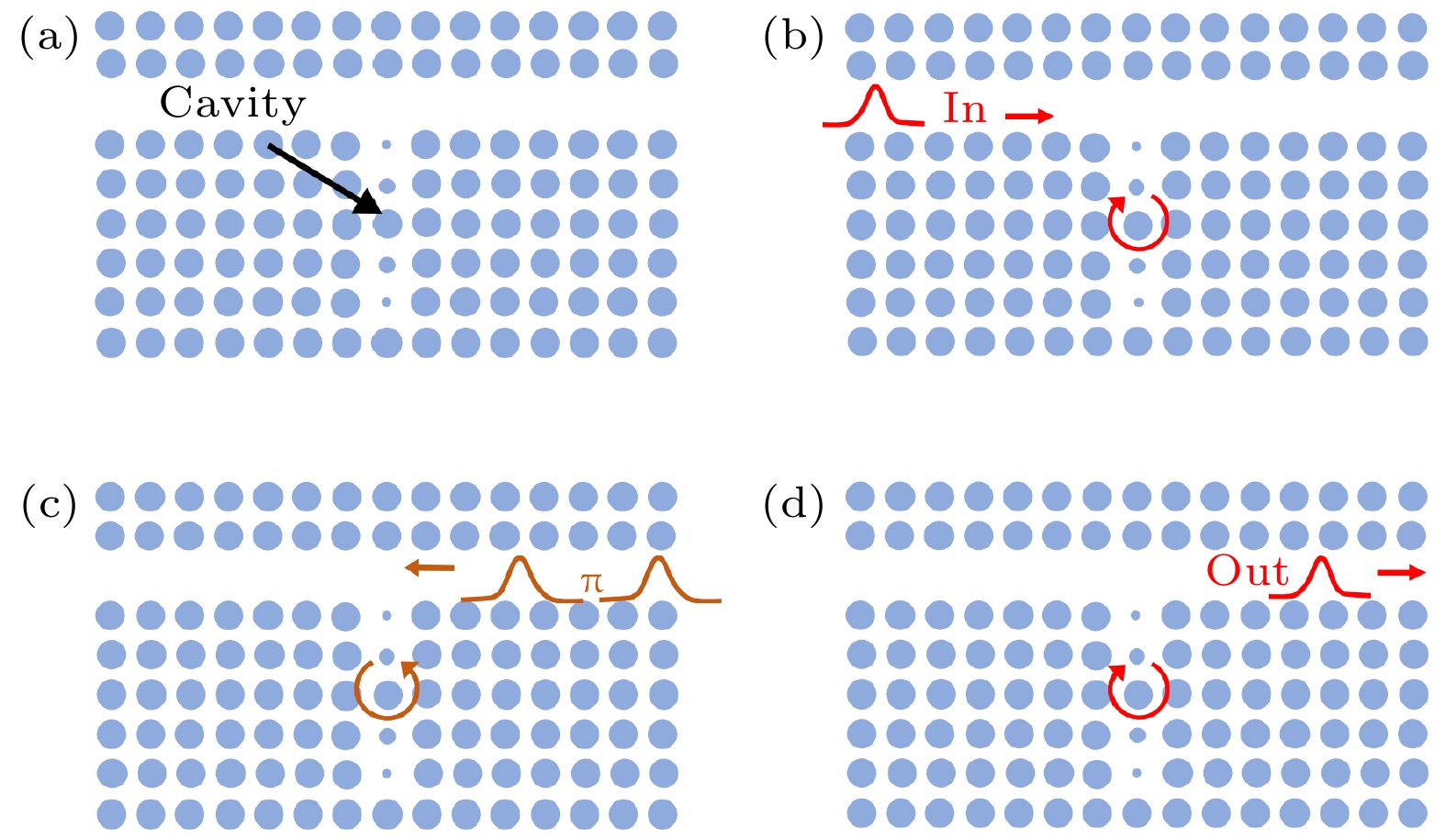
$ d_2 = 150 $ nm, one can make another kind of cavity that supports hexapole resonance. The field distribution is shown in panel (d). In such a structure the coupling between waveguides and the cavity are impedance matched, as shown in panel (f), therefore one can transfer the input light to the down-right port with an efficiency close to 100%
图 4 基于光子晶体微腔的ROSE回波量子存储 (a)用于ROSE存储的光子晶体结构; (b)信号光脉冲从左侧入射, 如图 3(d)所示, 可以在原子系统中激发出一种
$ \phi_0(r) $ 为“顺时针”旋转的集体极化; (c)控制$ \pi $ 脉冲从右侧入射, 因此其激发的腔模具有的相位分布$ \phi_1(r) $ 为“逆时针”旋转方向; (d) 当第二个控制$ \pi $ 脉冲也从右侧入射后, 根据(13)式和(15)式, 原子系统的集体激发再次具有$ \phi_0(r) $ 的相位分布, 在$ t = 2 t_2 - 2 t_1 + t_0 $ 时刻会向右边的端口外辐射出一个光子回波Figure 4. Protocol of ROSE quantum memory based on photonic crystal structures: (a) One photonic crystal structure that is suitable for ROSE technique; (b) a signal pulse is input from the left, and the collective atomic polarization thus has a “clockwise” spatial phase distribution
$ \phi_0(r) $ ; (c) control$ \pi $ pulses are input from the right, therefore have a “anti-clockwise” spatial phase distribution$ \phi_1(r) $ ; (d) after the second$ \pi $ pulse, according the Eqs. (13) and (15), the collective atomic polarization has a phase distribution of$ \phi_0(r) $ and then emit a photon echo to the right port -
[1] Lvovsky A I, Sanders B C, Tittel W 2009 Nat. Photonics 3 706
Google Scholar
[2] Sangouard N, Simon C, Riedmatten H D, Gisin N 2011 Rev. Mod. Phys. 83 33
Google Scholar
[3] Heshami K, England D G, Humphreys P C, Bustard P J, Acosta V M, Nunn J, Sussman B J 2016 J. Mod. Opt. 63 2005
Google Scholar
[4] Simon C 2017 Nat. Photonics 11 678
Google Scholar
[5] Kimble H J 2008 Nature 453 1023
Google Scholar
[6] Bussieres F, Sangouard N, Afzelius M, Riedmatten H D, Tittel W 2013 J. Mod. Opt. 60 1519
Google Scholar
[7] Saglamyurek E, Sinclair N, Jin J, Slater J A, Oblak D, Bussieres F, George M, Ricken R, Sohler W, Tittel W 2011 Nature 469 512
Google Scholar
[8] Liu C, Zhu T X, Su M X, Ma Y Z, Zhou Z Q, Li C F, Guo G C 2020 Phys. Rev. Lett. 125 260504
Google Scholar
[9] Liu C, Zhou Z Q, Zhu T X, Zheng L, Jin M, Liu X, Li P Y, Huang J Y, Ma Y, Tu T, Yang T S, Li C F, Guo G C 2020 Optica 7 192
[10] Zhong T, Kindem J M, Bartholomew J G, Rochman J, Craiciu I, Miyazono E, Bettinelli M, Cavalli E, Verma V, Nam S W, Marsili F, Shaw M D, Beyer A D, Faraon A 2017 Science 357 1392
Google Scholar
[11] Craiciu I, Lei M, Rochman J, Bartholomew J G, Faraon A 2021 Optica 8 114
[12] Hétet G, Longdell J J, Alexander A L, Lam P K, Sellars M J 2008 Phys. Rev. Lett. 100 23601
Google Scholar
[13] Moiseev S A, Kröll S 2001 Phys. Rev. Lett. 87 173601
[14] Kraus B, Tittel W, Gisin N, Nilsson M, Kröll S, Cirac J I Phys. Rev. A 73 020302
[15] Alexander A L, Longdell J J, Sellars M J, Manson N B 2006 Phys. Rev. Lett. 96 043602
Google Scholar
[16] Riedmatten H D, AfZelius M, Staudt M U, Simon C, Gisin N 2008 Nature 456 07607
[17] Mcauslan D L, Ledingham P M, Naylor W R, Beavan S E, Longdell J J 2011 Phys. Rev. A 84 022309
Google Scholar
[18] Afzelius M, Simon C, Riedmatten H De, Gisin N 2009 Phys. Rev. A 79 052329
Google Scholar
[19] Chanelière T, Hétet G 2015 Opt. Lett. 40 1294
Google Scholar
[20] McDonald H C 2016 Ph. D. Dissertation (Otago: University of Otago)
[21] Ma Y Z, Jin M, Chen D L, Zhou Z Q, Li C F, Guo G C 2021 Nat. Commun. 12 4378
Google Scholar
[22] Damon V, Bonarota M, Louchet-Chauvet A, Chaneliere T, Le Gouët J L 2011 New J. Phys. 13 093031
Google Scholar
[23] Dajczgewand J, Le Gouët J L, Louchet-Chauvet A, Chanelière T 2014 Opt. Lett. 39 2711
Google Scholar
[24] Fu Y, Wang M F, Zheng Y Z 2014 Opt. Commun. 321 162
Google Scholar
[25] Fan S, Villeneuve P R, Joannopoulos J D, Haus H A 1998 Opt. Express 3 4
[26] Afzelius1 M, Simon C 2010 Phys. Rev. A 82 022310
[27] Wang J, Sciarrino F, Laing A, Thompson M G 2020 Nat. Photonics 14 273
Google Scholar
[28] Zhong T, Goldner P 2019 Nanophotonics 8 2003
Google Scholar
[29] Hughes M A, Panjwani N A, Urdampilleta M, Homewood K P, Murdin B, Carey J D 2021 Appl. Phys. Lett. 118 194001
Google Scholar
[30] Yin C, Rancic M, Boo G G, Stavrias N, McCallum J C, Sellars M J, Rogge S 2013 Nature 497 91
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4448
- PDF Downloads: 135
- Cited By: 0
