非厄米系统的量子模拟新进展

高雪儿; 李代莉; 刘志航; 郑超

doi:10.7498/aps.71.20221825

摘要

量子模拟利用可控性好的量子系统模拟和研究可控性差或尚不能获得的量子系统, 是量子信息科学的主要研究内容之一. 量子模拟可通过量子计算机、量子信息处理器或小型量子设备实现. 非厄米系统近二十年来受到广泛关注, 一方面是因为非厄米量子理论可作为传统厄米量子力学理论的补充和延拓, 且与开放或耗散系统联系紧密. 另一方面, 可构造具有新奇非厄米性质的量子或经典系统, 具有提高精密测量精度等应用价值. 与厄米情况相比, 非厄米量子系统的时间演化不具有幺正性, 对其开展量子模拟研究具有一定的挑战. 本文介绍了非厄米系统量子模拟理论与实验新进展. 理论方面主要介绍了基于酉算子线性组合算法, 简单梳理了各个工作的优势和局限性, 并简要介绍了量子随机行走、嵌入式和空间拓展等量子模拟理论; 实验方面简要介绍了利用核磁共振量子系统、量子光学以及利用经典系统模拟非厄米量子系统的实验. 一方面, 这些新进展结合了量子模拟与非厄米领域的研究, 推动了非厄米系统本身的理论、实验和应用发展, 另一方面拓展了量子模拟和量子计算机的可应用范围.

关键词:

Abstract

Quantum simulation is one of the main contents of quantum information science, aiming to simulate and investigate poorly controllable or unobtainable quantum systems by using controllable quantum systems. Quantum simulation can be implemented in quantum computers, quantum simulators, and small quantum devices. Non-Hermitian systems have aroused research interest increasingly in recent two decades. On one hand, non-Hermitian quantum theories can be seen as the complex extensions of the conventional quantum mechanics, and are closely related to open systems and dissipative systems. On the other hand, both quantum systems and classical systems can be constructed as non-Hermitian systems with novel properties, which can be used to improve the precision of precise measurements. However, a non-Hermitian system is more difficult to simulate than a Hermitian system in that the time evolution of it is no longer unitary. In this review, we introduce recent research progress of quantum simulations of non-Hermitian systems. We mainly introduce theoretical researches to simulate typical non-Hermitian quantum systems by using the linear combinations of unitaries, briefly showing the advantages and limitations of each proposal, and we briefly mention other theoretical simulation methods, such as quantum random walk, space embedded and dilation. Moreover, we briefly introduce the experimental quantum simulations of non-Hermitian systems and novel phenomena in nuclear magnetic resonance, quantum optics and photonics, classical systems, etc. The recent progress of the combinations of quantum simulation and non-Hermitian physics has promoted the development of the non-Hermitian theories, experiments and applications, and expand the scope of application of quantum simulations and quantum computers.

Keywords:

作者及机构信息

北方工业大学理学院, 北京　100144

通信作者: 郑超, czheng@ncut.edu.cn

基金项目: 国家自然科学基金(批准号: 12175002, 11705004)、北京市自然科学基金(批准号: 1222020)和北京市教委优秀青年人才培育计划资助的课题

Authors and contacts

College of Science, North China Universty of Technology, Beijing 100144, China

Corresponding author: Zheng Chao, czheng@ncut.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 12175002, 11705004), the Natural Science Foundation of Beijing, China (Grant No. 1222020), and the Development of Talents Project for Outstanding Young Scholars of Beijing Municipal Institutions, China

文章全文 : translate this paragraph

参考文献

[1]	Pauli W 1943 Rev. Mod. Phys. 15 175 Google Scholar
[2]	Dirac P A M 1942 Proc. R. Soc. London, Ser. A 180 980 Google Scholar
[3]	Lee T D, Wick G C 1969 Nucl. Phys. B 9 209 Google Scholar
[4]	Ding P Z, Yi W 2022 Chin. Phys. B 31 010309 Google Scholar
[5]	Gamow G 1928 Zeitschrift für Physik 51 204 Google Scholar
[6]	Moiseyev N 2011 Non-Hermitian Quantum Mechanics (Cambridge: Cambridge University Press) pp211–247
[7]	Breuer H P, Petruccione F 2002 The Theory of Open Quantum Systems (10th Anniversary Ed.) (Oxford: Oxford University Press) pp421–431
[8]	Barreiro J T, Müller M, Schindler P, Nigg D, Monz T, Chwalla M, Hennrich M, Roos C F, Zoller P, Blatt R 2011 Nature 470 486 Google Scholar
[9]	Hu Z, Xia R, Kais S A 2020 Sci. Rep. 10 3301 Google Scholar
[10]	Del Re L, Rost B, Kemper A F, Freericks J K 2020 Phys. Rev. B 102 125112 Google Scholar
[11]	Viyuela O, Rivas A, Gasparinetti S, Wallraff A, Filipp S, Martin-Delgado M A 2018 npj Quantum Inf. 4 10 Google Scholar
[12]	Schlimgen A W, Head-Marsden K, Sager L M, Narang P, Mazziotti D A 2021 Phys. Rev. Lett. 127 270503 Google Scholar
[13]	Del Re L, Rost B, Foss-Feig M, Kemper A F, Freericks J K 2022 arXiv: 2204.12400[quant-ph]
[14]	Zheng C 2021 Sci. Rep. 11 3960 Google Scholar
[15]	陈曾军, 宁西京 2003 52 2683 Google Scholar Chen Z J, Ning X J 2003 Acta Phys. Sin. 52 2683 Google Scholar
[16]	Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243 Google Scholar
[17]	Bender C M, Brody D C, Jones H F 2004 Phys. Rev. D 70 025001 Google Scholar
[18]	Bender C M, Brody D C, Jones H F 2002 Phys. Rev. Lett. 89 270401 Google Scholar
[19]	Bender C M 2007 Rep. Prog. Phys. 70 947 Google Scholar
[20]	Mostafazadeh A 2002 J. Math. Phys. 43 205 Google Scholar
[21]	Mostafazadeh A 1998 J. Math. Phys. 39 4499 Google Scholar
[22]	Mostafazadeh A 2002 J. Math. Phys. 43 2814 Google Scholar
[23]	Mostafazadeh A 2002 Nucl. Phys. B 640 419 Google Scholar
[24]	Mostafazadeh A 2004 J. Math. Phys. 45 932 Google Scholar
[25]	Deutsch M 1985 Proc. R. Soc. London Ser. A 400 97 Google Scholar
[26]	Jin L, Song Z 2009 Phys. Rev. A 80 052107 Google Scholar
[27]	唐原江, 梁超, 刘永椿 2022 71 171101 Google Scholar Tang Y J, Liang C, Liu Y C 2022 Acta Phys. Sin. 71 171101 Google Scholar
[28]	张禧征, 王鹏, 张坤亮, 杨学敏, 宋智 2022 71 174501 Google Scholar Zhang, X Z, Wang P, Zhang K L, Yang X M, Song Z 2022 Acta Phys. Sin. 71 174501 Google Scholar
[29]	Kato T 1966 Perturbation Theory for Linear Operators (Berlin: Springer-Verlag) pp64–516
[30]	Heiss W D 2012 J. Phys. A: Math. Theor. 45 444016 Google Scholar
[31]	Regensburger A, Bersch C, Miri M A, Onishchukov G, Christodoulides D N, Peschel U 2012 Nature 488 167 Google Scholar
[32]	Hodaei H, Hassan A U, Wittek S, Garcia-Gracia H, El-Ganainy R, Christodoulides D N, Khajavikhan M 2017 Nature 548 187 Google Scholar
[33]	Rüter C E, Makris K G, El-Ganainy R, Christodoulides D N, Segev M, Kip D 2010 Nat. Phys. 6 192 Google Scholar
[34]	Wimmer M, Miri M A, Christodoulides D N, Peschel U 2015 Sci. Rep. 5 17760 Google Scholar
[35]	Feng L, Xu Y L, Fegadolli W S, Lu M H, Oliveira J E B, Almeida V R, Chen Y F, Scherer A 2013 Nat. Mater. 12 108 Google Scholar
[36]	Xu H, Mason D, Jiang L, Harris J G E 2016 Nature 537 80 Google Scholar
[37]	Yao R Z, Lee C, Podolskiy V, Guo W 2018 Laser Photonics Rev. 13 1800154 Google Scholar
[38]	Zheng C, Li D 2022 Sci. Rep. 12 2824 Google Scholar
[39]	Li D, Zheng C 2022 Entropy 2 4 Google Scholar
[40]	李丽娟, 明飞, 宋学科, 叶柳, 王栋 2022 71 070302 Google Scholar Li L J, Ming F, Song X K, Wang D 2022 Acta Phys. Sin. 71 070302 Google Scholar
[41]	Feynman R P 1982 Int. J. Theor. Phys. 21 467 Google Scholar
[42]	Greiner M, Mandel O, Esslinger T, Hansch T W, Bloch I 2002 Nature 415 39 Google Scholar
[43]	Gerritsma R, Kirchmair G, Zahringer F, Solano E, Blatt R, Roos C F 2010 Nature 463 68 Google Scholar
[44]	Pearson J, Feng G R, Zheng C, Long G L 2016 Sci. China Phys. Mech. Astron. 59 120312 Google Scholar
[45]	Sheng Y B, Zhou L 2017 Sci. Bull. 62 1025 Google Scholar
[46]	Georgescu I M, Ashhab S, Nori F 2014 Nature 86 153 Google Scholar
[47]	Zheng C, Hao L, Long G L 2013 Philol. Trans. R. Soc. A 371 20120053 Google Scholar
[48]	Gao T, Estrecho E, Bliokh K Y, Liew T C H, Fraser M D, Brodbeck S, Kamp M, Schneider C, Hofling S, Yamamoto Y 2015 Nature 526 554 Google Scholar
[49]	Zheng C, Wei S 2018 Int. J. Theor. Phys. 57 2203 Google Scholar
[50]	Wang H, Wei S, Zheng C, Kong X, Wen J, Nie X, Li J, Lu D, Xin T 2020 Phys. Rev. A 102 012610 Google Scholar
[51]	Zheng C 2018 EPL 123 40002 Google Scholar
[52]	Wen J, Zheng C, Kong X, Wei S, Xin T, Long G 2019 Phys. Rev. A 99 062122 Google Scholar
[53]	Li C, Wang P, Jin L, Song Z 2021 J. Phys. Commun. 5 105011 Google Scholar
[54]	Jin L 2022 Chin. Phys. Lett. 39 037302 Google Scholar
[55]	Zheng C 2019 EPL 126 30005 Google Scholar
[56]	Wen J, Qin G, Zheng C, Wei S, Kong X, Xin T, Long G 2020 npj Quantum Inf. 6 28 Google Scholar
[57]	Zheng C 2022 Chin. Phys. B 31 100301 Google Scholar
[58]	Joglekar Y N, Saxena A 2011 Phys. Rev. A 83 050101 Google Scholar
[59]	Valle G D, Longhi S 2013 Phys. Rev. A 87 022119 Google Scholar
[60]	Faisal F H M, Moloney J V 1981 J. Phys. B 14 3603 Google Scholar
[61]	Zhang S, Jin L, Song Z 2022 Chin. Phys. B 31 010312 Google Scholar
[62]	Jin L, Song Z 2010 Phys. Rev. A 81 032109 Google Scholar
[63]	胡洲, 曾招云, 唐佳, 罗小兵 2022 71 074207 Google Scholar Hu Z, Zeng Z Y, Tang J, Luo X B 2022 Acta Phys. Sin. 71 074207 Google Scholar
[64]	Cannata F, Junker G, Trost J 1998 Phys. Lett. A 246 219 Google Scholar
[65]	Chuang Y L, Ziauddin, Lee R K 2018 Opt. Express 26 17 Google Scholar
[66]	Benioff P 1980 J. Stat. Phys. 22 563 Google Scholar
[67]	Shor P W 1994 Proceeding of the 35th IEEE Symposium on Foundations of Computer Science Santa Fe, New Mexico, USA, November 20–22, 1994 p124
[68]	Grover L K 1996 Proceedings of the Twenty-eighth Annual ACM Aymposium on Theory of Computing Philadelphia, USA, July 1, 1996 p212
[69]	范桁 2018 67 120301 Google Scholar Fan H 2018 Acta Phys. Sin 67 120301 Google Scholar
[70]	Garcia-Perez G, Rossi M A C, Maniscalco S 2020 npj Quantum Inf. 6 1 Google Scholar
[71]	Wei S J, Ruan D, Long G L 2016 Sci. Rep. 6 30727 Google Scholar
[72]	Long G L 2006 Commun. Theor. Phys. 45 825 Google Scholar
[73]	Long G L 2011 Int. J. Theor. Phys. 50 1305 Google Scholar
[74]	Motta M, Sun C, Tan A T K, O’Rourke M J, Ye E, Minnich A J, Brandao F G S L, Chan G K L 2020 Nat. Phys. 16 205 Google Scholar
[75]	Kamakari H, Sun S N, Motta M, Minnich A J 2022 PRX Quantum 3 010320 Google Scholar
[76]	Endo S, Sun J, Li Y, Benjamin S C, Yuan X 2020 Phys. Rev. Lett. 125 010501 Google Scholar
[77]	Head-Marsden K, Krastanov S, Mazziotti D A, Narang P 2021 Phys. Rev. Res. 3 013182 Google Scholar
[78]	Hu Z, Head-Marsden K, Mazziotti D A, Narang P, Kais S 2022 Quantum 6 726 Google Scholar
[79]	Gudder S 2007 Quantum Inf. Process. 6 37 Google Scholar
[80]	Long G L, Liu Y 2008 Commun. Theor. Phys. 50 1303 Google Scholar
[81]	Long G L, Liu Y, Wang C 2009 Commun. Theor. Phys. 51 65 Google Scholar
[82]	Long G L 2007 Quantum Inf. Process. 6 49 Google Scholar
[83]	Cao H X, Long G L, Guo Z H 2013 Int. J. Theor. Phys. 52 1 Google Scholar
[84]	Cui J X, Zhou T, Long G L 2012 Quantum Inf. Process. 11 317 Google Scholar
[85]	Nielsen M A, Chuang I L 2002 Am. J. Phys. 70 558 Google Scholar
[86]	Penrose R 1971 Quantum Theory and Beyond (Cambridge: Cambridge University Press) pp151–180
[87]	Wen J W, Zheng C, Ye Z D, Xin T, Long G L 2021 Phys. Rev. Res. 3 013256 Google Scholar
[88]	Li X G, Zheng C, Gao J C, Long G L 2022 Phys. Rev. A 105 032405 Google Scholar
[89]	Shao C, Li Y, Li H 2019 J. Syst. Sci. Complex 32 375 Google Scholar
[90]	Günther N, Samsonov B F 2008 Phys. Rev. Lett. 101 230404 Google Scholar
[91]	Xiao L, Zhan X, Bian Z H, Wang K K, Zhang X, Wang X P, Li J, Mochizuki K, Kim D, Kawakami N, Yi W, Obuse H, Sanders B C, Xue P 2017 Nat. Phys. 13 1117 Google Scholar
[92]	Choi Y, Hahn C, Yoon J, Song S 2018 Nat. Commun. 9 2182 Google Scholar
[93]	Ge L, Tureci H E 2013 Phys. Rev. A 88 053810 Google Scholar
[94]	Yang F, Liu Y C, You L 2017 Phys. Rev. A 96 053845 Google Scholar
[95]	Li Y, Peng Y G, Han L, Miri M A, Li W, Xiao M, Zhu X F, Zhao J, Alu A, Fan S, Qiu C W 2019 Science 364 170 Google Scholar
[96]	Xu H S, Jin L 2021 Phys. Rev. A 104 012218 Google Scholar
[97]	Gao P, Sun Y, Liu X, Wang T, Wang C 2019 IEEE Access 7 107874 Google Scholar
[98]	Longhi S, Pinotti E 2019 EPL 125 10006 Google Scholar
[99]	Zheng C 2021 EPL 136 30002 Google Scholar
[100]	Zheng C 2022 Entropy 24 867 Google Scholar
[101]	Zheng C, Tian J, Li D L, Wen J W, Wei S J, Li Y S 2020 Entropy 22 812 Google Scholar
[102]	Gao W C, Zheng C, Liu L, Wang T J, Wang C 2021 Opt. Express 29 517 Google Scholar
[103]	Aharonov Y, Davidovich L, Zagury N 1993 Phys. Rev. A 48 1687 Google Scholar
[104]	Farhi E, Gutmann S 1998 Phys. Rev. A 58 915 Google Scholar
[105]	Watrous J 2001 J. Comput. Syst. Sci. 62 376 Google Scholar
[106]	Xue P, Zhang R, Qin H, Zhan X, Bian Z H, Li J, Sanders B C 2015 Phys. Rev. Lett. 114 140502 Google Scholar
[107]	Casanova J, Sabín C, León J, Egusquiza I L, Gerritsma R, Roos C F, García-Ripoll J J, Solano E 2011 Phys. Rev. X 1 021018 Google Scholar
[108]	Candia R D, Mejia B, Castillo H, Pedernales J S, Casanova J, Solano E 2013 Phys. Rev. Lett. 111 240502 Google Scholar
[109]	Alvarez-Rodriguez U, Casanova J, Lamata L, Solano E 2013 Phys. Rev. Lett. 111 090503 Google Scholar
[110]	Zhang X, Shen Y, Zhang J, Casanova J, Lamata L, Solano E, Yung M H, Zhang J N, Kim K 2015 Nat. Commun. 6 7917 Google Scholar
[111]	Keil R, Noh C, Rai A, Stützer S, Nolte S, Angelakis D G, Szameit A 2015 Optica 2 454 Google Scholar
[112]	Pedernales J S, Candia R D, Schindler P, Monz T, Hennrich M, Casanova J, Solano E 2014 Phys. Rev. A 90 012327 Google Scholar
[113]	Huang M, Kumar A, Wu J 2018 Phys. Lett. A 382 2578 Google Scholar
[114]	黄旻怡 2018 博士学位论文 (杭州: 浙江大学) Huang M 2018 Ph. D. Dissertation (Hang zhou: Zhejiang University) (in Chines)
[115]	Beneduci R 2020 J. Phys.: Conf. Ser. 1638 012006 Google Scholar
[116]	Bender C M, Brody D C, Jones H F, Meister B K 2007 Phys. Rev. Lett. 98 040403 Google Scholar
[117]	Holevo A S 1982 Probabilistic and Statistical Aspects of Quantum Theory (Amsterdam: North-Holland) pp127–140
[118]	孔祥宇, 朱垣晔, 闻经纬, 辛涛, 李可仁, 龙桂鲁 2018 68 220301 Google Scholar Kong X Y, Zhu Y Y, Wen J W, Xin T, Li K R, Long G L 2018 Acta Opt. Sin. 68 220301 Google Scholar
[119]	Long G L, Qin W, Yang Z, Li J L 2018 Sci. China: Phys. Mech. Astron. 61 030311 Google Scholar
[120]	Xin T, Li H, Wang B X, Long G L 2015 Phys. Rev. A 92 022126 Google Scholar
[121]	Peng X, Du J, Suter D 2005 Phys. Rev. A 71 012307 Google Scholar
[122]	Zhang J, Peng X, Rajendran N, Suter D 2008 Phys. Rev. Lett. 100 100501 Google Scholar
[123]	Feng G R, Lu Y, Hao L, Zhang F H, Long G L 2013 Sci. Rep. 3 2232 Google Scholar
[124]	Gunther N, Samsonov B F 2008 Phys. Rev. A 78 042115 Google Scholar
[125]	O’Neill P 2013 Dev. Growth Differ. 55 188 Google Scholar
[126]	Wiltschko W, Wiltschko R 1972 Science 176 62 Google Scholar
[127]	Ritz T, Thalau P, Phillips J B, Wiltschko R, Wiltschko W 2004 Nature 429 177 Google Scholar
[128]	Thalau P, Ritz T, Stapput K, Wiltschko R, Wiltschko W 2005 Naturwissenschaften 92 86 Google Scholar
[129]	Biskup T, Schleicher E, Okafuji A, Link G, Hitomi K, Getzoff E D, Weber S 2009 Angew. Chem. Int. Ed. 48 404 Google Scholar
[130]	Wiltschko W, Stapput K, Thalau P, Wiltschko R 2006 Naturwissenschaften 93 300 Google Scholar
[131]	Vandersypen L M K, Chuang I L 2005 Rev. Mod. Phys. 76 1037 Google Scholar
[132]	Han M, Huang W, Ma Y 2007 Int. J. Mod. Phys. D 16 1397 Google Scholar
[133]	Li K, Li Y N, Han M X, Lu S R, Zhou J, Ruan D, Long G L, Wan Y D, Lu D W, Zeng B, Laflamme R 2019 Commun. Phys. 2 122 Google Scholar
[134]	Rovelli C, Vidotto F 2014 Covariant Loop Quantum Gravity: An Elementary Introduction to Quantum Gravity and Spinfoam Theory. Cambridge Monographs on Mathematical Physics (Cambridge: Cambridge University Press) pp3–27
[135]	Perez A 2013 Living Rev. Rel. 16 3 Google Scholar
[136]	Tennant D A, Perring T G, Cowley R A, Nagler S E 1993 Phys. Rev. Lett. 70 4003 Google Scholar
[137]	Tennant D A, Cowley R A, Nagler S E, Tsvelik A M 1995 Phys. Rev. B 52 13368 Google Scholar
[138]	Liao Y A, Rittner A S C, Paprotta T, Li W, Partridge G B, Hulet R F, Baur S K, Mueller E J 2010 Nature 467 567 Google Scholar
[139]	Zheng C, Song S Y, Li J L, Long G L 2013 J. Opt. Soc. Am. B 30 1688 Google Scholar
[140]	Hu S W, Xue K, Ge M L 2008 Phys. Rev. A 78 022319 Google Scholar
[141]	Peterson J P S, Batalhão T B, Herrera M, Souza A M, Sarthour R S, Oliveira I S, Serra R M 2019 Phys. Rev. Lett. 123 240601 Google Scholar
[142]	Klatzow J, Becker J N, Ledingham P M, Weinzetl C, Kaczmarek K T, Saunders D J, Nunn J, Walmsley I A, Uzdin R, Poem E 2019 Phys. Rev. Lett. 122 110601 Google Scholar
[143]	Nielsen M A, Chuang I L 2011 Quantum Computation and Quantum Information (10th Ed.) (New York: Cambridge University Press) pp416–561
[144]	Salles A, de Melo F, Almeida M P, Hor-Meyll M, Walborn S P, Souto Ribeiro P H, Davidovich L 2008 Phys. Rev. A 78 022322 Google Scholar
[145]	Passos M H M, Santos Alan C, Sarandy Marcelo S, Huguenin J A O 2019 Phys. Rev. A 100 022113 Google Scholar
[146]	Xiao L, Wang K K, Zhan X, Bian Z H, Kawabata K, Ueda M, Yi W, Xue P 2019 Phys. Rev. Lett. 123 230401 Google Scholar
[147]	Lima G, Vargas A, Neves L, Guzmán R, Saavedra C 2009 Opt. Express 17 10688 Google Scholar
[148]	Machado P, Matoso A A, Barros M R, Neves L, Pádua S 2019 Phys. Rev. A 99 063839 Google Scholar
[149]	de Assis P L, Carvalho M A D, Berruezo L P, Ferraz J, Santos I F, Sciarrino F, Pádua S 2011 Opt. Express 19 3715 Google Scholar
[150]	Baldijão R D, Borges G F, Marques B, Solís-Prosser M A, Neves L, Pádua S 2017 Phys. Rev. A 96 032329 Google Scholar
[151]	Borges G F, Baldijão R D, CondáJ G L, Cabral J S, Marques B, Terra Cunha M, Cabello A, Pádua S 2018 Phys. Rev. A 97 022301 Google Scholar
[152]	Cardoso A C, CondéJ G L, Marques B, Cabral J S, Pádua S 2021 Phys. Rev. A 103 013722 Google Scholar
[153]	Maraviglia N, Yard P, Wakefield R, Carolan J, Sparrow C, Chakhmakhchyan L, Harrold C, Hashimoto T, Matsuda N, Harter A K, Joglekar Y N, Laing A 2022 Phys. Rev. Res. 4 013051 Google Scholar
[154]	Schindler J, Li A, Zheng M C, Ellis F M, Kottos T 2011 Phys. Rev. A 84 040101 Google Scholar
[155]	Lin Z, Schindler J, Ellis F M, Kottos T 2012 Phys. Rev. A 85 050101 Google Scholar
[156]	傅廷, 王宇飞, 王学友, 陈静瑄, 周旭彦, 郑婉华 2021 中国激光 48 1201005 Google Scholar Fu T, Wang Y F, Wang X Y, Chen J X, Zhou X Y, Zheng W H 2021 Chinese Journal of Lasers 48 1201005 Google Scholar
[157]	El-Ganainy R, Makris K G, Christodoulides D N, Musslimani Z H 2007 Opt. Lett. 32 002632 Google Scholar
[158]	Miri M, LiKamWa P, Christodoulides D N 2012 Opt. Lett. 37 000764 Google Scholar
[159]	Hodaei H, Miri M, Heinrich M, Christodoulides D N, Khajavikhan M 2014 SPIE Process. 9162 91621Q Google Scholar
[160]	Feng L, Wong Z J, Ma R M, Wang Y, Zhang X 2014 Science 346 972 Google Scholar
[161]	Gu Z Y, Zhang N, Lyu Q, Li M, Xiao S M, Song Q H 2016 Laser Photonics Rev. 10 588 Google Scholar
[162]	Miao P, Zhang Z, Sun J, Walasik W, Longhi S, Litchinitser N M, Feng L 2016 Science 353 464 Google Scholar
[163]	Zhang Z F, Qiao X D, Midya B, Liu K, Sun J B, Wu T W, Liu W J, Agarwal R, Jornet J M, Longhi S, Litchinitser N M, Feng L 2020 Science 368 760 Google Scholar
[164]	Xu H S, Jin L 2022 Phys. Rev. Res. 4 L032015 Google Scholar
[165]	Jin L, Song Z 2018 Phys. Rev. Lett. 121 073901 Google Scholar
[166]	成恩宏, 郎利君 2022 71 160301 Google Scholar Chen E H, Lang L J 2022 Acta Phys. Sin. 71 160301 Google Scholar

施引文献

图 1 PT对称和PPH系统的参数空间($ w, s, \theta $ 和$ v, u, \theta $, 设置$ r = 2 $)　(a) PT对称系统; (b) PPH系统^[38]

Fig. 1. Parameter spaces of PT-symmetric and P-pseudo-Hermitian systems ($ w, s, \theta $ and $ v, u, \theta $ with setting $ r = 2 $): (a) PT-symmetric systems; (b) PPH systems^[38]

下载: 全尺寸图片幻灯片

图 2 APT和APPH系统的参数空间($ w, s, \theta $和$ v, u, \theta $, 设置$ r = 2 $)　(a) APT系统; (b) APPH 系统^[38]

Fig. 2. Parameter spaces of APT-symmetric and anti-P-pseudo-Hermitian systems ($ w, s, \theta $ and $ v, u, \theta $ with setting $ r = 2 $): (a) APT-symmetric systems; (b) APPH systems^[38]

下载: 全尺寸图片幻灯片

图 3 广义PT对称二能级量子系统的量子线路^[51]

Fig. 3. Quantum circuit for a general PT-symmetric two-level system^[51]

下载: 全尺寸图片幻灯片

图 4 由辅助qutrit和辅助qudit构造广义PT对称二能级量子系统的电路图　(a)辅助qutrit; (b)辅助qudit^[51]

Fig. 4. Quantum circuit for a general PT-symmetric two-level system by ancillary qutrit or ancillary qudit: (a) Ancillary qutrit; (b) ancillary qudit^[51]

下载: 全尺寸图片幻灯片

图 5 模拟处于任意相的PT反对称二能级系统的量子线路^[55]

Fig. 5. Quantum circuit for a generalized APT-symmetric two-level system in arbitrary phase^[55]

下载: 全尺寸图片幻灯片

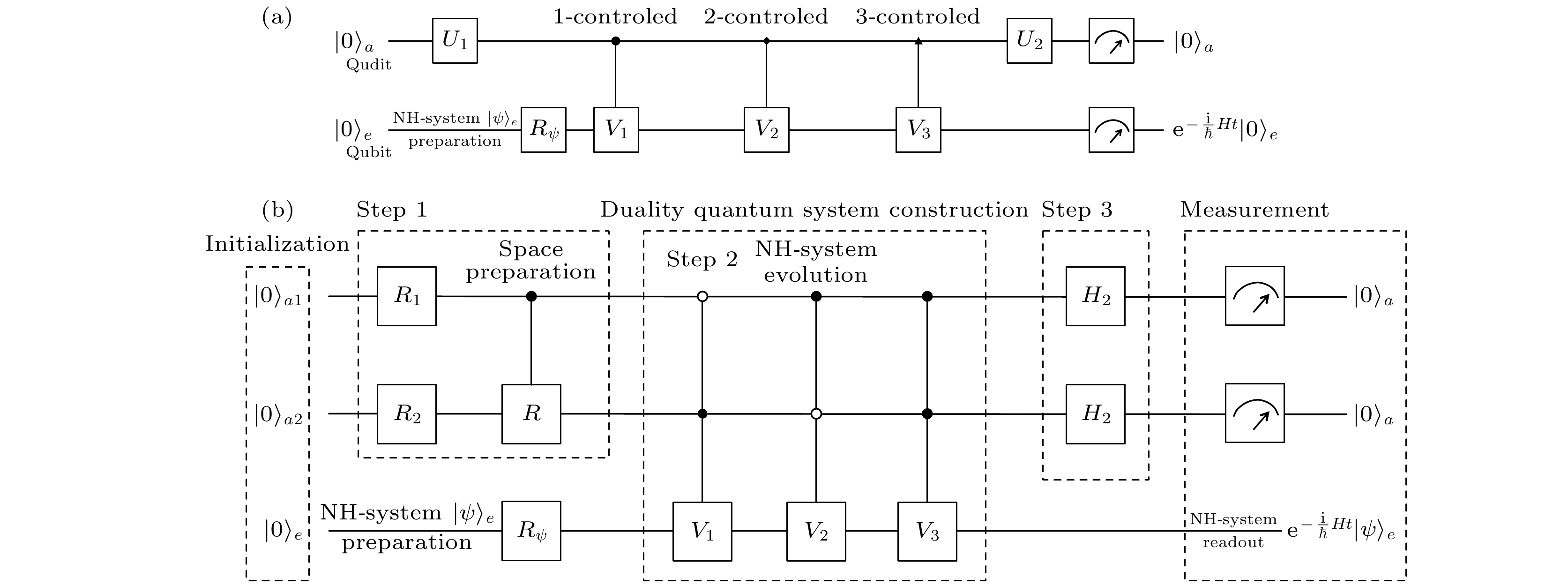
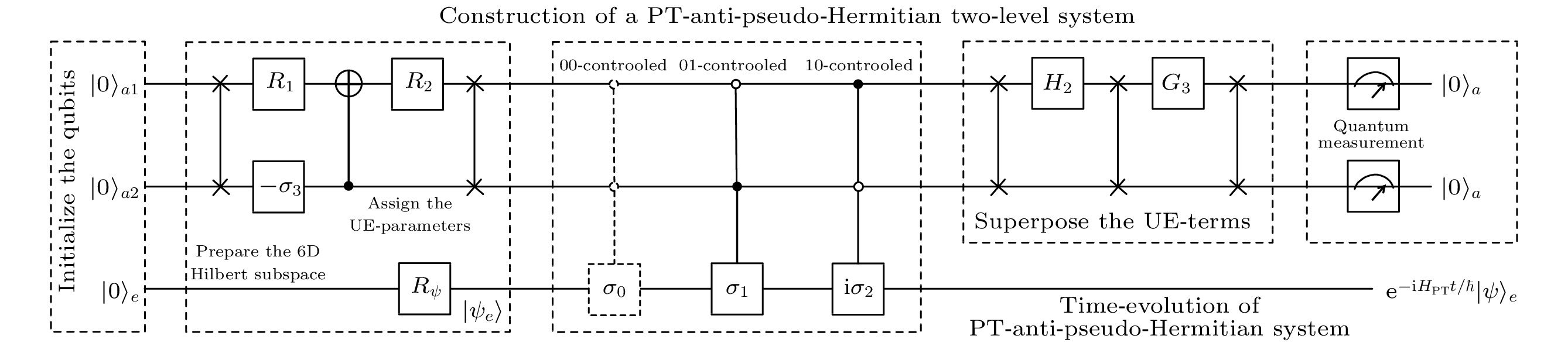
图 6 量子计算机的流程图和量子线路图　(a)模拟广义APT系统的流程图; (b)模拟广义APT系统的线路图; (c)第一次测量之后的初始化和空间准备的量子线路图; (d)第二次测量之后的量子线路图^[55]

Fig. 6. Flow chart and quantum circuit for a qubit computer: (a) Flow chart of quantum simulation of the generalized APT-symmetric system; (b) quantum circuit to simulate the evolution of the generalized APT-symmetric system; (c) quantum circuit for space preparation and initialization after the first measurement; (d) quantum circuit for initialization after the second measurement^[55]

下载: 全尺寸图片幻灯片

图 7 Qubit-qudit混合量子线路(由一个工作量子比特和四维辅助量子比特组成的混合系统)^[99]

Fig. 7. Qubit-qudit hybrid quantum circuit (The hybrid system consists of a work qubit and a four-dimensional ancillary qudit)^[99]

下载: 全尺寸图片幻灯片

图 8 三量子比特线路(由一个工作比特和两个辅助量子比特子系统构成)^[99]

Fig. 8. Three-qubit quantum circuit(consists of a work qubit and a two-qubit ancillary subsystems)^[99]

下载: 全尺寸图片幻灯片

图 9 (a) qubit-qutrit混合量子计算机的线路图; (b)三比特量子计算机的量子线路图^[101]

Fig. 9. (a) Quantum circuit for a qubit-qutrit hybrid computer; (b) quantum circuit designed for a quantum computer of three qubits^[101]

下载: 全尺寸图片幻灯片

图 10 (a) qubit-qudit混合量子计算机的线路图; (b)六维子空间中三量子比特量子计算机的线路图^[101]

Fig. 10. (a) Quantum circuit for a qubit-qudit hybrid computer; (b) quantum circuit designed for a quantum computer of three qubits using the full Hilbert space^[101]

下载: 全尺寸图片幻灯片

图 11 模拟T-APH二能级系统的三量子比特线路图^[57]

Fig. 11. Three-qubit quantum circuit to simulate a T-anti-pseudo-Hermitian two-level system^[57]

下载: 全尺寸图片幻灯片

图 12 模拟PT-APH二能级系统的三量子比特线路图^[57]

Fig. 12. Three-qubit quantum circuit to simulate a general PT-anti-pseudo-Hermitian two-level system^[57]

下载: 全尺寸图片幻灯片

图 13 由制备、演化和检测三个模块组成的实验装置^[102]

Fig. 13. Experimental configuration includes three modules: the preparation module, the evolution and the detection part^[102]

下载: 全尺寸图片幻灯片

图 14 可区分性测量的信息流实验结果^[56]

Fig. 14. Experimental results of information flow measured by distinguishability^[56]

下载: 全尺寸图片幻灯片

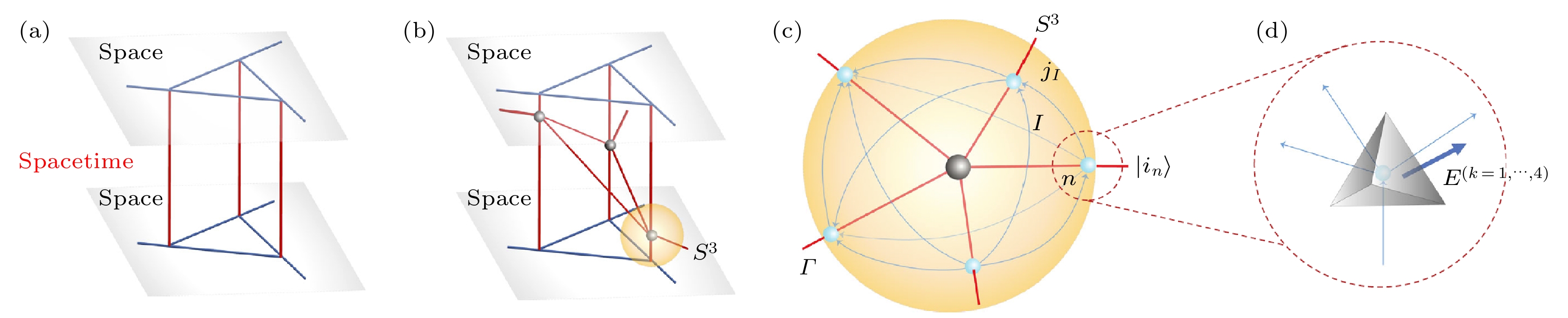
图 15 量子时空和四面体　(a)静态四维(4D) 量子时空; (b)五价点的动态量子时空; (c) S ³ 的局域结构; (d)量子几何四面体^[133]

Fig. 15. Quantum spacetime and tetrahedra: (a) A static 4D quantum spacetime; (b) a dynamical quantum spacetime with a number of five valent vertices; (c) the local structure of S ³; (d) quantum geometrical tetrahedra^[133]

下载: 全尺寸图片幻灯片

图 16 实验制备量子态在Bloch 球上的对应和相关经典的四面体^[133]

Fig. 16. Experimentally prepared states on the Bloch sphere and their corresponding classical tetrahedra^[133]

下载: 全尺寸图片幻灯片

图 17 LCU模拟YBE的简图^[49]

Fig. 17. Schematic illustration of the LCU simulation of the YBE by quantum optics system and a nuclear magnetic resonance quantum system^[49]

下载: 全尺寸图片幻灯片

图 18 用于准备和实现在三模平行高斯光束状态下的算符的实验装置^[152]

Fig. 18. Experimental setup used to prepare and to implement the operations on a three-path parallel Gaussian beam state^[152]

下载: 全尺寸图片幻灯片

map

[1]	Pauli W 1943 Rev. Mod. Phys. 15 175 Google Scholar
[2]	Dirac P A M 1942 Proc. R. Soc. London, Ser. A 180 980 Google Scholar
[3]	Lee T D, Wick G C 1969 Nucl. Phys. B 9 209 Google Scholar
[4]	Ding P Z, Yi W 2022 Chin. Phys. B 31 010309 Google Scholar
[5]	Gamow G 1928 Zeitschrift für Physik 51 204 Google Scholar
[6]	Moiseyev N 2011 Non-Hermitian Quantum Mechanics (Cambridge: Cambridge University Press) pp211–247
[7]	Breuer H P, Petruccione F 2002 The Theory of Open Quantum Systems (10th Anniversary Ed.) (Oxford: Oxford University Press) pp421–431
[8]	Barreiro J T, Müller M, Schindler P, Nigg D, Monz T, Chwalla M, Hennrich M, Roos C F, Zoller P, Blatt R 2011 Nature 470 486 Google Scholar
[9]	Hu Z, Xia R, Kais S A 2020 Sci. Rep. 10 3301 Google Scholar
[10]	Del Re L, Rost B, Kemper A F, Freericks J K 2020 Phys. Rev. B 102 125112 Google Scholar
[11]	Viyuela O, Rivas A, Gasparinetti S, Wallraff A, Filipp S, Martin-Delgado M A 2018 npj Quantum Inf. 4 10 Google Scholar
[12]	Schlimgen A W, Head-Marsden K, Sager L M, Narang P, Mazziotti D A 2021 Phys. Rev. Lett. 127 270503 Google Scholar
[13]	Del Re L, Rost B, Foss-Feig M, Kemper A F, Freericks J K 2022 arXiv: 2204.12400[quant-ph]
[14]	Zheng C 2021 Sci. Rep. 11 3960 Google Scholar
[15]	陈曾军, 宁西京 2003 52 2683 Google Scholar Chen Z J, Ning X J 2003 Acta Phys. Sin. 52 2683 Google Scholar
[16]	Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243 Google Scholar
[17]	Bender C M, Brody D C, Jones H F 2004 Phys. Rev. D 70 025001 Google Scholar
[18]	Bender C M, Brody D C, Jones H F 2002 Phys. Rev. Lett. 89 270401 Google Scholar
[19]	Bender C M 2007 Rep. Prog. Phys. 70 947 Google Scholar
[20]	Mostafazadeh A 2002 J. Math. Phys. 43 205 Google Scholar
[21]	Mostafazadeh A 1998 J. Math. Phys. 39 4499 Google Scholar
[22]	Mostafazadeh A 2002 J. Math. Phys. 43 2814 Google Scholar
[23]	Mostafazadeh A 2002 Nucl. Phys. B 640 419 Google Scholar
[24]	Mostafazadeh A 2004 J. Math. Phys. 45 932 Google Scholar
[25]	Deutsch M 1985 Proc. R. Soc. London Ser. A 400 97 Google Scholar
[26]	Jin L, Song Z 2009 Phys. Rev. A 80 052107 Google Scholar
[27]	唐原江, 梁超, 刘永椿 2022 71 171101 Google Scholar Tang Y J, Liang C, Liu Y C 2022 Acta Phys. Sin. 71 171101 Google Scholar
[28]	张禧征, 王鹏, 张坤亮, 杨学敏, 宋智 2022 71 174501 Google Scholar Zhang, X Z, Wang P, Zhang K L, Yang X M, Song Z 2022 Acta Phys. Sin. 71 174501 Google Scholar
[29]	Kato T 1966 Perturbation Theory for Linear Operators (Berlin: Springer-Verlag) pp64–516
[30]	Heiss W D 2012 J. Phys. A: Math. Theor. 45 444016 Google Scholar
[31]	Regensburger A, Bersch C, Miri M A, Onishchukov G, Christodoulides D N, Peschel U 2012 Nature 488 167 Google Scholar
[32]	Hodaei H, Hassan A U, Wittek S, Garcia-Gracia H, El-Ganainy R, Christodoulides D N, Khajavikhan M 2017 Nature 548 187 Google Scholar
[33]	Rüter C E, Makris K G, El-Ganainy R, Christodoulides D N, Segev M, Kip D 2010 Nat. Phys. 6 192 Google Scholar
[34]	Wimmer M, Miri M A, Christodoulides D N, Peschel U 2015 Sci. Rep. 5 17760 Google Scholar
[35]	Feng L, Xu Y L, Fegadolli W S, Lu M H, Oliveira J E B, Almeida V R, Chen Y F, Scherer A 2013 Nat. Mater. 12 108 Google Scholar
[36]	Xu H, Mason D, Jiang L, Harris J G E 2016 Nature 537 80 Google Scholar
[37]	Yao R Z, Lee C, Podolskiy V, Guo W 2018 Laser Photonics Rev. 13 1800154 Google Scholar
[38]	Zheng C, Li D 2022 Sci. Rep. 12 2824 Google Scholar
[39]	Li D, Zheng C 2022 Entropy 2 4 Google Scholar
[40]	李丽娟, 明飞, 宋学科, 叶柳, 王栋 2022 71 070302 Google Scholar Li L J, Ming F, Song X K, Wang D 2022 Acta Phys. Sin. 71 070302 Google Scholar
[41]	Feynman R P 1982 Int. J. Theor. Phys. 21 467 Google Scholar
[42]	Greiner M, Mandel O, Esslinger T, Hansch T W, Bloch I 2002 Nature 415 39 Google Scholar
[43]	Gerritsma R, Kirchmair G, Zahringer F, Solano E, Blatt R, Roos C F 2010 Nature 463 68 Google Scholar
[44]	Pearson J, Feng G R, Zheng C, Long G L 2016 Sci. China Phys. Mech. Astron. 59 120312 Google Scholar
[45]	Sheng Y B, Zhou L 2017 Sci. Bull. 62 1025 Google Scholar
[46]	Georgescu I M, Ashhab S, Nori F 2014 Nature 86 153 Google Scholar
[47]	Zheng C, Hao L, Long G L 2013 Philol. Trans. R. Soc. A 371 20120053 Google Scholar
[48]	Gao T, Estrecho E, Bliokh K Y, Liew T C H, Fraser M D, Brodbeck S, Kamp M, Schneider C, Hofling S, Yamamoto Y 2015 Nature 526 554 Google Scholar
[49]	Zheng C, Wei S 2018 Int. J. Theor. Phys. 57 2203 Google Scholar
[50]	Wang H, Wei S, Zheng C, Kong X, Wen J, Nie X, Li J, Lu D, Xin T 2020 Phys. Rev. A 102 012610 Google Scholar
[51]	Zheng C 2018 EPL 123 40002 Google Scholar
[52]	Wen J, Zheng C, Kong X, Wei S, Xin T, Long G 2019 Phys. Rev. A 99 062122 Google Scholar
[53]	Li C, Wang P, Jin L, Song Z 2021 J. Phys. Commun. 5 105011 Google Scholar
[54]	Jin L 2022 Chin. Phys. Lett. 39 037302 Google Scholar
[55]	Zheng C 2019 EPL 126 30005 Google Scholar
[56]	Wen J, Qin G, Zheng C, Wei S, Kong X, Xin T, Long G 2020 npj Quantum Inf. 6 28 Google Scholar
[57]	Zheng C 2022 Chin. Phys. B 31 100301 Google Scholar
[58]	Joglekar Y N, Saxena A 2011 Phys. Rev. A 83 050101 Google Scholar
[59]	Valle G D, Longhi S 2013 Phys. Rev. A 87 022119 Google Scholar
[60]	Faisal F H M, Moloney J V 1981 J. Phys. B 14 3603 Google Scholar
[61]	Zhang S, Jin L, Song Z 2022 Chin. Phys. B 31 010312 Google Scholar
[62]	Jin L, Song Z 2010 Phys. Rev. A 81 032109 Google Scholar
[63]	胡洲, 曾招云, 唐佳, 罗小兵 2022 71 074207 Google Scholar Hu Z, Zeng Z Y, Tang J, Luo X B 2022 Acta Phys. Sin. 71 074207 Google Scholar
[64]	Cannata F, Junker G, Trost J 1998 Phys. Lett. A 246 219 Google Scholar
[65]	Chuang Y L, Ziauddin, Lee R K 2018 Opt. Express 26 17 Google Scholar
[66]	Benioff P 1980 J. Stat. Phys. 22 563 Google Scholar
[67]	Shor P W 1994 Proceeding of the 35th IEEE Symposium on Foundations of Computer Science Santa Fe, New Mexico, USA, November 20–22, 1994 p124
[68]	Grover L K 1996 Proceedings of the Twenty-eighth Annual ACM Aymposium on Theory of Computing Philadelphia, USA, July 1, 1996 p212
[69]	范桁 2018 67 120301 Google Scholar Fan H 2018 Acta Phys. Sin 67 120301 Google Scholar
[70]	Garcia-Perez G, Rossi M A C, Maniscalco S 2020 npj Quantum Inf. 6 1 Google Scholar
[71]	Wei S J, Ruan D, Long G L 2016 Sci. Rep. 6 30727 Google Scholar
[72]	Long G L 2006 Commun. Theor. Phys. 45 825 Google Scholar
[73]	Long G L 2011 Int. J. Theor. Phys. 50 1305 Google Scholar
[74]	Motta M, Sun C, Tan A T K, O’Rourke M J, Ye E, Minnich A J, Brandao F G S L, Chan G K L 2020 Nat. Phys. 16 205 Google Scholar
[75]	Kamakari H, Sun S N, Motta M, Minnich A J 2022 PRX Quantum 3 010320 Google Scholar
[76]	Endo S, Sun J, Li Y, Benjamin S C, Yuan X 2020 Phys. Rev. Lett. 125 010501 Google Scholar
[77]	Head-Marsden K, Krastanov S, Mazziotti D A, Narang P 2021 Phys. Rev. Res. 3 013182 Google Scholar
[78]	Hu Z, Head-Marsden K, Mazziotti D A, Narang P, Kais S 2022 Quantum 6 726 Google Scholar
[79]	Gudder S 2007 Quantum Inf. Process. 6 37 Google Scholar
[80]	Long G L, Liu Y 2008 Commun. Theor. Phys. 50 1303 Google Scholar
[81]	Long G L, Liu Y, Wang C 2009 Commun. Theor. Phys. 51 65 Google Scholar
[82]	Long G L 2007 Quantum Inf. Process. 6 49 Google Scholar
[83]	Cao H X, Long G L, Guo Z H 2013 Int. J. Theor. Phys. 52 1 Google Scholar
[84]	Cui J X, Zhou T, Long G L 2012 Quantum Inf. Process. 11 317 Google Scholar
[85]	Nielsen M A, Chuang I L 2002 Am. J. Phys. 70 558 Google Scholar
[86]	Penrose R 1971 Quantum Theory and Beyond (Cambridge: Cambridge University Press) pp151–180
[87]	Wen J W, Zheng C, Ye Z D, Xin T, Long G L 2021 Phys. Rev. Res. 3 013256 Google Scholar
[88]	Li X G, Zheng C, Gao J C, Long G L 2022 Phys. Rev. A 105 032405 Google Scholar
[89]	Shao C, Li Y, Li H 2019 J. Syst. Sci. Complex 32 375 Google Scholar
[90]	Günther N, Samsonov B F 2008 Phys. Rev. Lett. 101 230404 Google Scholar
[91]	Xiao L, Zhan X, Bian Z H, Wang K K, Zhang X, Wang X P, Li J, Mochizuki K, Kim D, Kawakami N, Yi W, Obuse H, Sanders B C, Xue P 2017 Nat. Phys. 13 1117 Google Scholar
[92]	Choi Y, Hahn C, Yoon J, Song S 2018 Nat. Commun. 9 2182 Google Scholar
[93]	Ge L, Tureci H E 2013 Phys. Rev. A 88 053810 Google Scholar
[94]	Yang F, Liu Y C, You L 2017 Phys. Rev. A 96 053845 Google Scholar
[95]	Li Y, Peng Y G, Han L, Miri M A, Li W, Xiao M, Zhu X F, Zhao J, Alu A, Fan S, Qiu C W 2019 Science 364 170 Google Scholar
[96]	Xu H S, Jin L 2021 Phys. Rev. A 104 012218 Google Scholar
[97]	Gao P, Sun Y, Liu X, Wang T, Wang C 2019 IEEE Access 7 107874 Google Scholar
[98]	Longhi S, Pinotti E 2019 EPL 125 10006 Google Scholar
[99]	Zheng C 2021 EPL 136 30002 Google Scholar
[100]	Zheng C 2022 Entropy 24 867 Google Scholar
[101]	Zheng C, Tian J, Li D L, Wen J W, Wei S J, Li Y S 2020 Entropy 22 812 Google Scholar
[102]	Gao W C, Zheng C, Liu L, Wang T J, Wang C 2021 Opt. Express 29 517 Google Scholar
[103]	Aharonov Y, Davidovich L, Zagury N 1993 Phys. Rev. A 48 1687 Google Scholar
[104]	Farhi E, Gutmann S 1998 Phys. Rev. A 58 915 Google Scholar
[105]	Watrous J 2001 J. Comput. Syst. Sci. 62 376 Google Scholar
[106]	Xue P, Zhang R, Qin H, Zhan X, Bian Z H, Li J, Sanders B C 2015 Phys. Rev. Lett. 114 140502 Google Scholar
[107]	Casanova J, Sabín C, León J, Egusquiza I L, Gerritsma R, Roos C F, García-Ripoll J J, Solano E 2011 Phys. Rev. X 1 021018 Google Scholar
[108]	Candia R D, Mejia B, Castillo H, Pedernales J S, Casanova J, Solano E 2013 Phys. Rev. Lett. 111 240502 Google Scholar
[109]	Alvarez-Rodriguez U, Casanova J, Lamata L, Solano E 2013 Phys. Rev. Lett. 111 090503 Google Scholar
[110]	Zhang X, Shen Y, Zhang J, Casanova J, Lamata L, Solano E, Yung M H, Zhang J N, Kim K 2015 Nat. Commun. 6 7917 Google Scholar
[111]	Keil R, Noh C, Rai A, Stützer S, Nolte S, Angelakis D G, Szameit A 2015 Optica 2 454 Google Scholar
[112]	Pedernales J S, Candia R D, Schindler P, Monz T, Hennrich M, Casanova J, Solano E 2014 Phys. Rev. A 90 012327 Google Scholar
[113]	Huang M, Kumar A, Wu J 2018 Phys. Lett. A 382 2578 Google Scholar
[114]	黄旻怡 2018 博士学位论文 (杭州: 浙江大学) Huang M 2018 Ph. D. Dissertation (Hang zhou: Zhejiang University) (in Chines)
[115]	Beneduci R 2020 J. Phys.: Conf. Ser. 1638 012006 Google Scholar
[116]	Bender C M, Brody D C, Jones H F, Meister B K 2007 Phys. Rev. Lett. 98 040403 Google Scholar
[117]	Holevo A S 1982 Probabilistic and Statistical Aspects of Quantum Theory (Amsterdam: North-Holland) pp127–140
[118]	孔祥宇, 朱垣晔, 闻经纬, 辛涛, 李可仁, 龙桂鲁 2018 68 220301 Google Scholar Kong X Y, Zhu Y Y, Wen J W, Xin T, Li K R, Long G L 2018 Acta Opt. Sin. 68 220301 Google Scholar
[119]	Long G L, Qin W, Yang Z, Li J L 2018 Sci. China: Phys. Mech. Astron. 61 030311 Google Scholar
[120]	Xin T, Li H, Wang B X, Long G L 2015 Phys. Rev. A 92 022126 Google Scholar
[121]	Peng X, Du J, Suter D 2005 Phys. Rev. A 71 012307 Google Scholar
[122]	Zhang J, Peng X, Rajendran N, Suter D 2008 Phys. Rev. Lett. 100 100501 Google Scholar
[123]	Feng G R, Lu Y, Hao L, Zhang F H, Long G L 2013 Sci. Rep. 3 2232 Google Scholar
[124]	Gunther N, Samsonov B F 2008 Phys. Rev. A 78 042115 Google Scholar
[125]	O’Neill P 2013 Dev. Growth Differ. 55 188 Google Scholar
[126]	Wiltschko W, Wiltschko R 1972 Science 176 62 Google Scholar
[127]	Ritz T, Thalau P, Phillips J B, Wiltschko R, Wiltschko W 2004 Nature 429 177 Google Scholar
[128]	Thalau P, Ritz T, Stapput K, Wiltschko R, Wiltschko W 2005 Naturwissenschaften 92 86 Google Scholar
[129]	Biskup T, Schleicher E, Okafuji A, Link G, Hitomi K, Getzoff E D, Weber S 2009 Angew. Chem. Int. Ed. 48 404 Google Scholar
[130]	Wiltschko W, Stapput K, Thalau P, Wiltschko R 2006 Naturwissenschaften 93 300 Google Scholar
[131]	Vandersypen L M K, Chuang I L 2005 Rev. Mod. Phys. 76 1037 Google Scholar
[132]	Han M, Huang W, Ma Y 2007 Int. J. Mod. Phys. D 16 1397 Google Scholar
[133]	Li K, Li Y N, Han M X, Lu S R, Zhou J, Ruan D, Long G L, Wan Y D, Lu D W, Zeng B, Laflamme R 2019 Commun. Phys. 2 122 Google Scholar
[134]	Rovelli C, Vidotto F 2014 Covariant Loop Quantum Gravity: An Elementary Introduction to Quantum Gravity and Spinfoam Theory. Cambridge Monographs on Mathematical Physics (Cambridge: Cambridge University Press) pp3–27
[135]	Perez A 2013 Living Rev. Rel. 16 3 Google Scholar
[136]	Tennant D A, Perring T G, Cowley R A, Nagler S E 1993 Phys. Rev. Lett. 70 4003 Google Scholar
[137]	Tennant D A, Cowley R A, Nagler S E, Tsvelik A M 1995 Phys. Rev. B 52 13368 Google Scholar
[138]	Liao Y A, Rittner A S C, Paprotta T, Li W, Partridge G B, Hulet R F, Baur S K, Mueller E J 2010 Nature 467 567 Google Scholar
[139]	Zheng C, Song S Y, Li J L, Long G L 2013 J. Opt. Soc. Am. B 30 1688 Google Scholar
[140]	Hu S W, Xue K, Ge M L 2008 Phys. Rev. A 78 022319 Google Scholar
[141]	Peterson J P S, Batalhão T B, Herrera M, Souza A M, Sarthour R S, Oliveira I S, Serra R M 2019 Phys. Rev. Lett. 123 240601 Google Scholar
[142]	Klatzow J, Becker J N, Ledingham P M, Weinzetl C, Kaczmarek K T, Saunders D J, Nunn J, Walmsley I A, Uzdin R, Poem E 2019 Phys. Rev. Lett. 122 110601 Google Scholar
[143]	Nielsen M A, Chuang I L 2011 Quantum Computation and Quantum Information (10th Ed.) (New York: Cambridge University Press) pp416–561
[144]	Salles A, de Melo F, Almeida M P, Hor-Meyll M, Walborn S P, Souto Ribeiro P H, Davidovich L 2008 Phys. Rev. A 78 022322 Google Scholar
[145]	Passos M H M, Santos Alan C, Sarandy Marcelo S, Huguenin J A O 2019 Phys. Rev. A 100 022113 Google Scholar
[146]	Xiao L, Wang K K, Zhan X, Bian Z H, Kawabata K, Ueda M, Yi W, Xue P 2019 Phys. Rev. Lett. 123 230401 Google Scholar
[147]	Lima G, Vargas A, Neves L, Guzmán R, Saavedra C 2009 Opt. Express 17 10688 Google Scholar
[148]	Machado P, Matoso A A, Barros M R, Neves L, Pádua S 2019 Phys. Rev. A 99 063839 Google Scholar
[149]	de Assis P L, Carvalho M A D, Berruezo L P, Ferraz J, Santos I F, Sciarrino F, Pádua S 2011 Opt. Express 19 3715 Google Scholar
[150]	Baldijão R D, Borges G F, Marques B, Solís-Prosser M A, Neves L, Pádua S 2017 Phys. Rev. A 96 032329 Google Scholar
[151]	Borges G F, Baldijão R D, CondáJ G L, Cabral J S, Marques B, Terra Cunha M, Cabello A, Pádua S 2018 Phys. Rev. A 97 022301 Google Scholar
[152]	Cardoso A C, CondéJ G L, Marques B, Cabral J S, Pádua S 2021 Phys. Rev. A 103 013722 Google Scholar
[153]	Maraviglia N, Yard P, Wakefield R, Carolan J, Sparrow C, Chakhmakhchyan L, Harrold C, Hashimoto T, Matsuda N, Harter A K, Joglekar Y N, Laing A 2022 Phys. Rev. Res. 4 013051 Google Scholar
[154]	Schindler J, Li A, Zheng M C, Ellis F M, Kottos T 2011 Phys. Rev. A 84 040101 Google Scholar
[155]	Lin Z, Schindler J, Ellis F M, Kottos T 2012 Phys. Rev. A 85 050101 Google Scholar
[156]	傅廷, 王宇飞, 王学友, 陈静瑄, 周旭彦, 郑婉华 2021 中国激光 48 1201005 Google Scholar Fu T, Wang Y F, Wang X Y, Chen J X, Zhou X Y, Zheng W H 2021 Chinese Journal of Lasers 48 1201005 Google Scholar
[157]	El-Ganainy R, Makris K G, Christodoulides D N, Musslimani Z H 2007 Opt. Lett. 32 002632 Google Scholar
[158]	Miri M, LiKamWa P, Christodoulides D N 2012 Opt. Lett. 37 000764 Google Scholar
[159]	Hodaei H, Miri M, Heinrich M, Christodoulides D N, Khajavikhan M 2014 SPIE Process. 9162 91621Q Google Scholar
[160]	Feng L, Wong Z J, Ma R M, Wang Y, Zhang X 2014 Science 346 972 Google Scholar
[161]	Gu Z Y, Zhang N, Lyu Q, Li M, Xiao S M, Song Q H 2016 Laser Photonics Rev. 10 588 Google Scholar
[162]	Miao P, Zhang Z, Sun J, Walasik W, Longhi S, Litchinitser N M, Feng L 2016 Science 353 464 Google Scholar
[163]	Zhang Z F, Qiao X D, Midya B, Liu K, Sun J B, Wu T W, Liu W J, Agarwal R, Jornet J M, Longhi S, Litchinitser N M, Feng L 2020 Science 368 760 Google Scholar
[164]	Xu H S, Jin L 2022 Phys. Rev. Res. 4 L032015 Google Scholar
[165]	Jin L, Song Z 2018 Phys. Rev. Lett. 121 073901 Google Scholar
[166]	成恩宏, 郎利君 2022 71 160301 Google Scholar Chen E H, Lang L J 2022 Acta Phys. Sin. 71 160301 Google Scholar

[1]	刘辉, 陆展鹏, 徐志浩. 一维非厄米十字晶格中的退局域-局域转变. , 2024, 73(13): 137201. doi: 10.7498/aps.73.20240510
[2]	李竞, 丁海涛, 张丹伟. 非厄米哈密顿量中的量子Fisher信息与参数估计. , 2023, 72(20): 200601. doi: 10.7498/aps.72.20230862
[3]	徐达, 王逸璞, 李铁夫, 游建强. 微波驱动下超导量子比特与磁振子的相干耦合. , 2022, 71(15): 150302. doi: 10.7498/aps.71.20220260
[4]	王晨旭, 贺冉, 李睿睿, 陈炎, 房鼎, 崔金明, 黄运锋, 李传锋, 郭光灿. 量子计算与量子模拟中离子阱结构研究进展. , 2022, 71(13): 133701. doi: 10.7498/aps.71.20220224
[5]	罗雨晨, 李晓鹏. 相互作用费米子的量子模拟. , 2022, 71(22): 226701. doi: 10.7498/aps.71.20221756
[6]	陈阳, 张天炀, 郭光灿, 任希锋. 基于集成光芯片的量子模拟研究进展. , 2022, 71(24): 244207. doi: 10.7498/aps.71.20221938
[7]	侯博, 曾琦波. 非厄米镶嵌型二聚化晶格. , 2022, 71(13): 130302. doi: 10.7498/aps.71.20220890
[8]	祝可嘉, 郭志伟, 陈鸿. 实验观测非厄米系统奇异点的手性翻转现象. , 2022, 71(13): 131101. doi: 10.7498/aps.71.20220842
[9]	成恩宏, 郎利君. 非互易Aubry-André 模型的经典电路模拟. , 2022, 71(16): 160301. doi: 10.7498/aps.71.20220219
[10]	孙思彤, 丁应星, 刘伍明. 基于线性与非线性干涉仪的量子精密测量研究进展. , 2022, 71(13): 130701. doi: 10.7498/aps.71.20220425
[11]	张禧征, 王鹏, 张坤亮, 杨学敏, 宋智. 非厄米临界动力学及其在量子多体系统中的应用. , 2022, 71(17): 174501. doi: 10.7498/aps.71.20220914
[12]	林键, 叶梦, 朱家纬, 李晓鹏. 机器学习辅助绝热量子算法设计. , 2021, 70(14): 140306. doi: 10.7498/aps.70.20210831
[13]	鹿博, 王大军. 超冷极性分子. , 2019, 68(4): 043301. doi: 10.7498/aps.68.20182274
[14]	朱燕清, 张丹伟, 朱诗亮. 用光晶格模拟狄拉克、外尔和麦克斯韦方程. , 2019, 68(4): 046701. doi: 10.7498/aps.68.20181929
[15]	赵兴东, 张莹莹, 刘伍明. 光晶格中超冷原子系统的磁激发. , 2019, 68(4): 043703. doi: 10.7498/aps.68.20190153
[16]	孔祥宇, 朱垣晔, 闻经纬, 辛涛, 李可仁, 龙桂鲁. 核磁共振量子信息处理研究的新进展. , 2018, 67(22): 220301. doi: 10.7498/aps.67.20180754
[17]	赵士平, 刘玉玺, 郑东宁. 新型超导量子比特及量子物理问题的研究. , 2018, 67(22): 228501. doi: 10.7498/aps.67.20180845
[18]	喻祥敏, 谭新生, 于海峰, 于扬. 利用超导量子电路模拟拓扑量子材料. , 2018, 67(22): 220302. doi: 10.7498/aps.67.20181857
[19]	范桁. 量子计算与量子模拟. , 2018, 67(12): 120301. doi: 10.7498/aps.67.20180710
[20]	赖云忠, 梁九卿. 哈密顿算符是SU(1,1)和SU(2)算子含时线性组合量子系统的时间演变及厄密不变量. , 1996, 45(5): 738-746. doi: 10.7498/aps.45.738

计量

文章访问数: 6908
PDF下载量: 342
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

非厄米系统的量子模拟新进展