-
We theoretically study the band structure, tunneling dynamics, and tunneling probability of tunable spin-orbit-coupled Bose-Einstein condensates under the periodic driving of Raman coupling. The time-independent Floquet Hamiltonian is obtained in the high-frequency approximation. It is found that the periodic driving can effectively tune spin-orbit coupling and nonlinear interaction. The system is mapped to a standard nonlinear two-level model, and the critical condition for the appearance of the loop in energy band structure and the width of the loop are obtained analytically. When the interspecies atomic interaction is equal to the intraspecies atomic interaction, there is no loop. However, when the intraspecies atomic interaction is smaller (larger) than the interspecies atomic interaction, the loop appears in the lower (upper) energy band. In this case, both spin-orbit coupling and Raman coupling will suppress the appearance of loop. In particular, the critical condition for the appearance of loop structure can be controlled by adjusting external driving. We also study the tunneling dynamics of Bose-Einstein condensate with tunable spin-orbit coupling. More importantly, by tuning the periodic driving, the tunneling dynamics of the system and the location of nonlinear Landau-Zener tunneling can be controlled. We also find that the spin components of the system can be reversed. Finally, the Landau-Zener tunneling probability of the system is calculated. The research shows that the periodic driving can effectively change the tunneling probability of the system.
-
Keywords:
- Bose-Einstein condensates /
- tunable spin-orbit coupling /
- nonlinear band structure /
- Landau-Zener tunneling
[1] Goldman N, Juzeliunas G, Öhberg P, Spielman I B 2014 Rep. Prog. Phys. 77 126401
Google Scholar
[2] Zhai H 2015 Rep. Prog. Phys. 78 026001
Google Scholar
[3] Zhang S, Jo G B 2019 J. Phys. Chem. Solids 128 75
Google Scholar
[4] Lin Y J, Jiménez-García K, Spielman I B 2011 Nature 471 83
[5] Wang C, Gao C, Jian C M, Zhai H 2010 Phys. Rev. Lett. 105 160403
Google Scholar
[6] Li Y, Pitaevskii L P, Stringari S 2012 Phys. Rev. Lett. 108 225301
Google Scholar
[7] Ho T L, Zhang S 2011 Phys. Rev. Lett. 107 150403
Google Scholar
[8] Jian C M, Zhai H 2011 Phys. Rev. B 84 060508
Google Scholar
[9] Zhou X F, Zhou J, Wu C 2011 Phys. Rev. A 84 063624
Google Scholar
[10] Xu Y, Mao L, Wu B, Zhang C 2014 Phys. Rev. Lett. 113 130404
Google Scholar
[11] Xu X Q, Han J H 2011 Phys. Rev. Lett. 107 200401
Google Scholar
[12] Radic J, Sedrakyan T A, Spielman I B, Galitski V 2011 Phys. Rev. A 84 063604
Google Scholar
[13] Xu P, Yi S, Zhang W 2019 Phys. Rev. Lett. 123 073001
Google Scholar
[14] van der Bijl E, Duine R A 2011 Phys. Rev. Lett. 107 195302
Google Scholar
[15] Grass T, Saha K, Sengupta K, Lewenstein M 2011 Phys. Rev. A 84 053632
Google Scholar
[16] Li Y, Martone G I, Pitaevski L P, Stringari S 2013 Phys. Rev. Lett. 110 235302
Google Scholar
[17] Li S, Wang H, Li F, Cui X, Liu B 2020 Phys. Rev. A 102 033328
Google Scholar
[18] Zhang Y, Mao L, Zhang C 2012 Phys. Rev. Lett. 108 035302
Google Scholar
[19] Zhang D W, Xue Z Y, Yan H, Wang Z D, Zhu S L 2012 Phys. Rev. A 85 013628
[20] Wu C J, Mondragon-Shem I, Zhou X F 2011 Chin. Phys. Lett. 28 097102
Google Scholar
[21] Sinha S, Nath R, Santos L 2011 Phys. Rev. Lett. 107 270401
Google Scholar
[22] Zhang J Y, Ji S C, Chen Z, Zhang L, Du Z D, Yan B, Pan G S, Zhao B, Deng Y J, Zhai H, Chen S, Pan J W 2012 Phys. Rev. Lett. 109 115301
Google Scholar
[23] Zheng W, Yu Z Q, Cui X, Zhai H 2013 J. Phys. B: At. Mol. Opt. Phys. 46 134007
Google Scholar
[24] Ji S C, Zhang L, Xu X T, Wu Z, Deng Y, Chen S, Pan J W 2015 Phys. Rev. Lett. 114 105301
Google Scholar
[25] Olson A J, Wang S J, Niffenegger R J, Li C H, Greene C H, Chen Y P 2014 Phys. Rev. A 90 013616
Google Scholar
[26] Xiong B, Zheng J H, Wang D W 2015 Phys. Rev. A 91 063602
Google Scholar
[27] Llorente J M G, Plata J 2016 Phys. Rev. A 94 053605
Google Scholar
[28] Wu H, Wang B Q, An J H 2021 Phys. Rev. B 103 L041115
Google Scholar
[29] Jiménez-García K, LeBlanc L J, Williams R A, Beeler M C, Qu C, Gong M, Zhang C, Spielman I B 2015 Phys. Rev. Lett. 114 125301
Google Scholar
[30] Zhang Y, Chen G, Zhang C 2013 Sci. Rep. 3 1937
Google Scholar
[31] Li J R, Lee J, Huang W, Burchesky S, Shteynas B, Top F C, Jamison A O, Ketterle W 2017 Nature 543 91
Google Scholar
[32] Yao J, Zhang S 2014 Phys. Rev. A 90 023608
Google Scholar
[33] Olson A J, Blasing D B, Qu C, Li C H, Niffenegger R J, Zhang C, Chen Y P 2017 Phys. Rev. A 95 043623
[34] Gomez Llorente J M, Plata J 2016 Phys. Rev. A 93 063633
Google Scholar
[35] Abdullaev F Kh, Salerno M 2018 Phys. Rev. A 98 053606
Google Scholar
[36] Liang J C, Zhang Y C, Jiao C, Zhang A X, Xue J K 2021 Phys. Rev. E 103 022204
[37] Zhang Y, Mossman M E, Busch T, Engels P, Zhang C 2016 Front. Phys. 11 118103
Google Scholar
[38] Liu J, Fu L, Ou B Y, Chen S G, Choi D I, Wu B, Niu Q 2002 Phys. Rev. A 66 023404
Google Scholar
[39] Zhang Y, Gui Z, Chen Y 2019 Phys. Rev. A 99 023616
Google Scholar
[40] 刘杰 2009 玻色-爱因斯坦凝聚体动力学: 非线性隧穿、相干及不稳定性 (北京: 科学出版社) 第40—50页
Liu J 2009 Dynamics of Bose-Einstein Condensates: Nonlinear Tunneling, Coherence, and Instability (Beijing: Science Press) pp40–50 (in Chinese)
[41] Wu B, Qian N 2003 New J. Phys. 5 104
Google Scholar
-
图 1 动量空间中不同相互作用关系下的能带结构 (a1), (a2)
$g=0.0<g_{12}=0.7$ ; (b1), (b2)$g=g_{12}=0.7$ ; (c1), (c2)$g= $ $ 1.5 > g_{12}=0.7$ Figure 1. Energy band structure in momentum space under different interactions: (a1), (a2)
$g=0.0<g_{12}=0.7$ ; (b1), (b2)$g=g_{12}= $ $ 0.7$ ; (c1), (c2)$g=1.5>g_{12}=0.7$ 
图 2 不同周期驱动强度下能带出现loop结构的临界拉曼耦合
$\varOmega_{0}$ 随种内原子间相互作用的变化规律.$g_{12}=0.7$ . 图中“Loop down”表示loop出现在下能带, “Loop up”表示loop出现在上能带Figure 2. Critical Raman coupling
$\varOmega_{0}$ as a function of intraspecies atomic interaction for different periodic driving strength with$g_{12}=0.7$ . “Loop down” means that the loop appears in lower band, while “Loop up” means that the loop appears in upper band
图 3 不同种内原子间相互作用下出现loop的临界拉曼耦合
$\varOmega_{0}$ 随周期驱动强度$\chi$ 的变化规律 (a)$g<g_{12}$ ; (b)$g>g_{12}$ .$g_{12}=0.7$ . 图中“Loop down”表示loop出现在下能带, “Loop up”表示loop出现在上能带Figure 3. Critical Raman coupling
$\varOmega_{0}$ as a function of periodic driving strength for different intraspecies atomic interaction: (a)$g<g_{12}$ ; (b)$g>g_{12}$ . The other parameters are$g_{12}=0.7$ . “Loop down” means that the loop appears in lower band, while “Loop up” means that the loop appears in upper band
图 4 (a1), (a2)
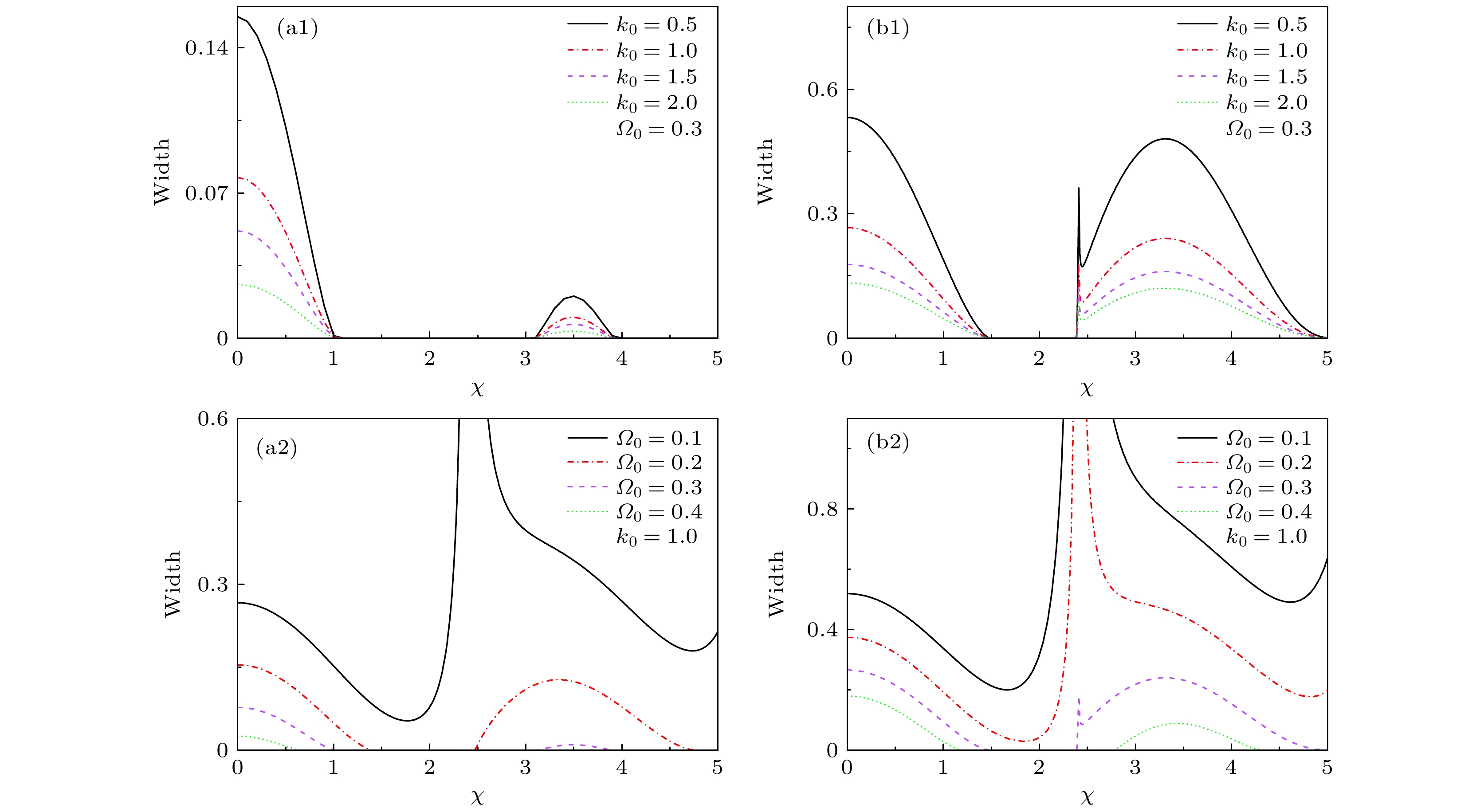
$g<g_{12}$ ($g=0.2< g_{12}=0.7$ )时不同自旋-轨道耦合强度$k_{0}$ 下loop宽度随$\chi$ 的变化规律($\varOmega_{0}=0.3$ ); (b1), (b2)$g> $ $ g_{12}$ ($g=1.5> g_{12}=0.7$ )时不同拉曼耦合$\varOmega_{0}$ 下loop宽度随$\chi$ 的变化规律($k_{0}=1$ )Figure 4. (a1), (a2) Loop width as a function of
$\chi$ for various spin-orbit coupled strength$k_{0}$ when$g<g_{12}$ ($ g=0.2< g_{12}=0.7$ ) with$\varOmega_{0}=0.3$ ; (b1), (b2) loop width as a function of$\chi$ for various Raman coupling$\varOmega_{0}$ when$g>g_{12}$ ($ g=1.5> g_{12}=0.7 $ ) with$k_{0}=1$ .
图 5 (a1)—(e1)存在loop结构时的能带结构, 原子最初制备在系统的上 (下) 能带用正方形(圆)标记; (a2)—(e2)原子初始制备在上能带中时对应的非线性朗道-齐纳隧穿动力学; (a3)—(e3)原子初始制备在下能带中时对应的非线性朗道-齐纳隧穿动力学. 第一行至第四行分别取
$\chi=0$ , 1, 2, 3, 4.$k_{0}=1$ ,$\varOmega_{0}=0.3$ ,$g=1.5$ ,$g_{12}=0.7$ ,$\alpha=0.0001$ Figure 5. (a1)−(e1) Energy band structure. The Bose-Einstein condensates are initially prepared in the lower (upper) band of the system labeled by the square (circle). (a2)−(e2) The corresponding nonlinear Landau-Zener tunneling dynamics when the atomics are initially prepared in the upper band. (a3)−(e3) The corresponding nonlinear Landau-Zener tunneling dynamics when the atomics are initially prepared in the lower band. From the first row to the fourth row:
$\chi=0, 1, 2, 3, 4$ , respectively. The other parameters are$k_{0}=1, \varOmega_{0}=0.3, g=1.5, g_{12}=0.7, \alpha=0.0001$ 
图 6 不同周期驱动强度
$\chi$ 下朗道-齐纳隧穿率随(a)自旋-轨道耦合强度$k_{0}$ 和(b)拉曼耦合$\varOmega_{0}$ 的变化规律 (a)$\varOmega_{0}=0.03$ ; (b)$k_{0}= $ $ 1.0$ . 不同形状的符号代表方程 (12) 给出的理论值, 不同的线条代表从方程 (8) 得到的数值解.$g=g_{12}=0.02$ ,$\alpha=0.001$ Figure 6. The Landau-Zener tunneling probabilities as a function of (a) the spin-orbit coupling strength
$k_{0}$ and (b) Raman coupling$\varOmega_{0}$ for various periodic driving strength$\chi$ : (a)$\varOmega_{0}=0.03$ ; (b)$k_{0}=1.0$ . The different symbols represent the theoretical values given by Eq. (12) and different lines represent the results obtained by Eq. (8). The other parameters are$g=g_{12}=0.02, \alpha=0.001$ 
图 7 不同周期驱动强度下非线性朗道-齐纳隧穿率随(a)拉曼耦合
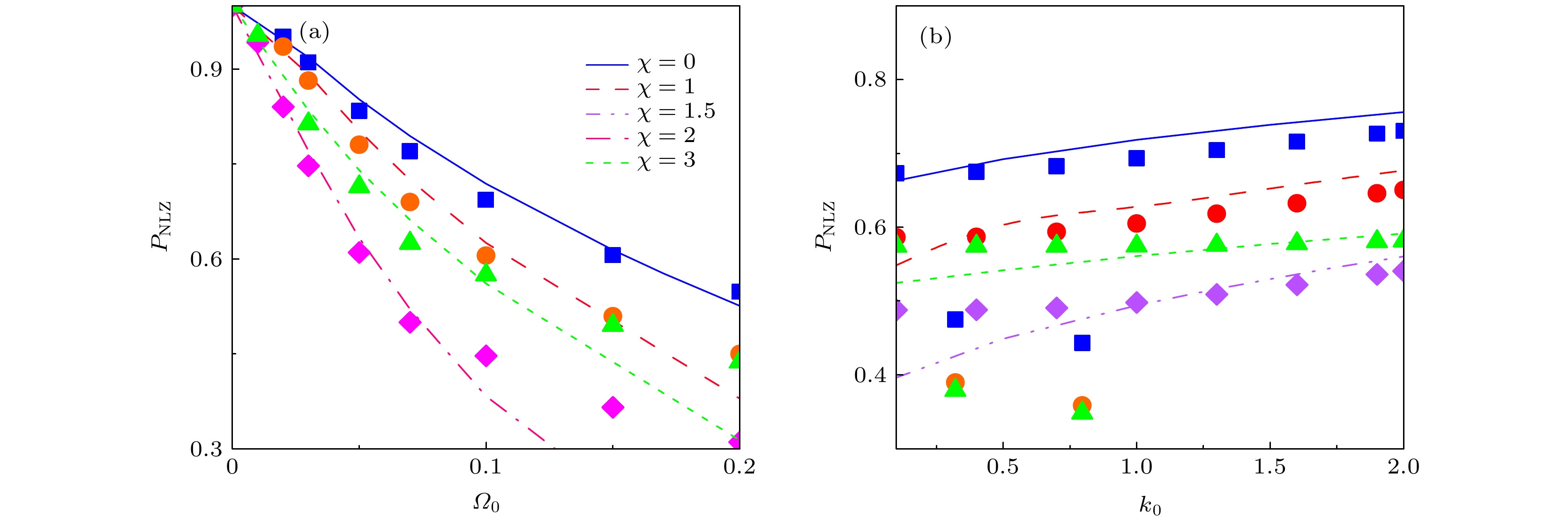
$\varOmega_{0}$ 和(b)自旋-轨道耦合强度$k_{0}$ 的变化规律 (a)$k_{0}=1$ ; (b)$\varOmega_{0}=0.1$ . 不同形状的符号代表方程 (14) 给出的理论值, 不同的线条代表从方程 (8) 得到的数值解.$g=1.5>g_{12}=0.7$ ,$\alpha=0.005$ Figure 7. The nonlinear Landau-Zener tunneling probabilities as a function of (a) Raman coupling
$\varOmega_{0}$ and (b) the spin-orbit coupling strength$k_{0}$ for various periodic driving strength$\chi$ . (a)$k_{0}=1$ , (b)$\varOmega_{0}=0.1$ . The different symbols represent the theoretical values given by Eq. (14) and different lines represent the results obtained by Eq. (8). The other parameters are$g=1.5 > $ $ g_{12}=0.7, \;\alpha=0.005$ -
[1] Goldman N, Juzeliunas G, Öhberg P, Spielman I B 2014 Rep. Prog. Phys. 77 126401
Google Scholar
[2] Zhai H 2015 Rep. Prog. Phys. 78 026001
Google Scholar
[3] Zhang S, Jo G B 2019 J. Phys. Chem. Solids 128 75
Google Scholar
[4] Lin Y J, Jiménez-García K, Spielman I B 2011 Nature 471 83
[5] Wang C, Gao C, Jian C M, Zhai H 2010 Phys. Rev. Lett. 105 160403
Google Scholar
[6] Li Y, Pitaevskii L P, Stringari S 2012 Phys. Rev. Lett. 108 225301
Google Scholar
[7] Ho T L, Zhang S 2011 Phys. Rev. Lett. 107 150403
Google Scholar
[8] Jian C M, Zhai H 2011 Phys. Rev. B 84 060508
Google Scholar
[9] Zhou X F, Zhou J, Wu C 2011 Phys. Rev. A 84 063624
Google Scholar
[10] Xu Y, Mao L, Wu B, Zhang C 2014 Phys. Rev. Lett. 113 130404
Google Scholar
[11] Xu X Q, Han J H 2011 Phys. Rev. Lett. 107 200401
Google Scholar
[12] Radic J, Sedrakyan T A, Spielman I B, Galitski V 2011 Phys. Rev. A 84 063604
Google Scholar
[13] Xu P, Yi S, Zhang W 2019 Phys. Rev. Lett. 123 073001
Google Scholar
[14] van der Bijl E, Duine R A 2011 Phys. Rev. Lett. 107 195302
Google Scholar
[15] Grass T, Saha K, Sengupta K, Lewenstein M 2011 Phys. Rev. A 84 053632
Google Scholar
[16] Li Y, Martone G I, Pitaevski L P, Stringari S 2013 Phys. Rev. Lett. 110 235302
Google Scholar
[17] Li S, Wang H, Li F, Cui X, Liu B 2020 Phys. Rev. A 102 033328
Google Scholar
[18] Zhang Y, Mao L, Zhang C 2012 Phys. Rev. Lett. 108 035302
Google Scholar
[19] Zhang D W, Xue Z Y, Yan H, Wang Z D, Zhu S L 2012 Phys. Rev. A 85 013628
[20] Wu C J, Mondragon-Shem I, Zhou X F 2011 Chin. Phys. Lett. 28 097102
Google Scholar
[21] Sinha S, Nath R, Santos L 2011 Phys. Rev. Lett. 107 270401
Google Scholar
[22] Zhang J Y, Ji S C, Chen Z, Zhang L, Du Z D, Yan B, Pan G S, Zhao B, Deng Y J, Zhai H, Chen S, Pan J W 2012 Phys. Rev. Lett. 109 115301
Google Scholar
[23] Zheng W, Yu Z Q, Cui X, Zhai H 2013 J. Phys. B: At. Mol. Opt. Phys. 46 134007
Google Scholar
[24] Ji S C, Zhang L, Xu X T, Wu Z, Deng Y, Chen S, Pan J W 2015 Phys. Rev. Lett. 114 105301
Google Scholar
[25] Olson A J, Wang S J, Niffenegger R J, Li C H, Greene C H, Chen Y P 2014 Phys. Rev. A 90 013616
Google Scholar
[26] Xiong B, Zheng J H, Wang D W 2015 Phys. Rev. A 91 063602
Google Scholar
[27] Llorente J M G, Plata J 2016 Phys. Rev. A 94 053605
Google Scholar
[28] Wu H, Wang B Q, An J H 2021 Phys. Rev. B 103 L041115
Google Scholar
[29] Jiménez-García K, LeBlanc L J, Williams R A, Beeler M C, Qu C, Gong M, Zhang C, Spielman I B 2015 Phys. Rev. Lett. 114 125301
Google Scholar
[30] Zhang Y, Chen G, Zhang C 2013 Sci. Rep. 3 1937
Google Scholar
[31] Li J R, Lee J, Huang W, Burchesky S, Shteynas B, Top F C, Jamison A O, Ketterle W 2017 Nature 543 91
Google Scholar
[32] Yao J, Zhang S 2014 Phys. Rev. A 90 023608
Google Scholar
[33] Olson A J, Blasing D B, Qu C, Li C H, Niffenegger R J, Zhang C, Chen Y P 2017 Phys. Rev. A 95 043623
[34] Gomez Llorente J M, Plata J 2016 Phys. Rev. A 93 063633
Google Scholar
[35] Abdullaev F Kh, Salerno M 2018 Phys. Rev. A 98 053606
Google Scholar
[36] Liang J C, Zhang Y C, Jiao C, Zhang A X, Xue J K 2021 Phys. Rev. E 103 022204
[37] Zhang Y, Mossman M E, Busch T, Engels P, Zhang C 2016 Front. Phys. 11 118103
Google Scholar
[38] Liu J, Fu L, Ou B Y, Chen S G, Choi D I, Wu B, Niu Q 2002 Phys. Rev. A 66 023404
Google Scholar
[39] Zhang Y, Gui Z, Chen Y 2019 Phys. Rev. A 99 023616
Google Scholar
[40] 刘杰 2009 玻色-爱因斯坦凝聚体动力学: 非线性隧穿、相干及不稳定性 (北京: 科学出版社) 第40—50页
Liu J 2009 Dynamics of Bose-Einstein Condensates: Nonlinear Tunneling, Coherence, and Instability (Beijing: Science Press) pp40–50 (in Chinese)
[41] Wu B, Qian N 2003 New J. Phys. 5 104
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4168
- PDF Downloads: 114
- Cited By: 0
