-
The physical properties and dynamics of molecules can be studied by the interaction between electromagnetic field and molecular system. The continuous development of terahertz technology provides a terahertz source capable of generating a sub-picosecond directional intense electric field. The generated intense-field terahertz wave has the same electric field intensity as the molecular local electric field environment, and on a sub-picosecond time scale of the directional electric field there can happen many ultrafast physical and chemical reactions. At present, the interaction between terahertz waves and molecules is limited mainly to the resonance interaction, that is, the molecules transition at different vibrational levels, caused through dipole interaction. In this work, based on the density functional theory calculation and the finite difference time domain solution method of Schrödinger equation, the intense non-resonance effect of intense terahertz wave electric field on hydrogen molecules is studied. The results show that under the action of intense terahertz wave sub-picosecond directional intense electric field, hydrogen molecule will produce an induced dipole moment. This dipole interacts with the external terahertz field, resulting in the fluctuation of proton probability density distribution and the change of vibration energy level population. Based on the non-resonant interaction between non-polar diatomic molecule hydrogen and intense terahertz wave, a unique way of producing the interaction between electromagnetic waves and molecules is displayed in this work, which is a method of studying the dynamics of non-polar molecules and molecules with weak polarity in intense terahertz field.
-
Keywords:
- hydrogen molecule /
- terahertz wave /
- non-resonance /
- induce dipole moment
[1] Stapelfeldt H 2003 Eur. Phys. J. D 26 15
Google Scholar
[2] Sakai H, Safvan C P, Larsen J J, Hilligsoe K M, Hald K, Stapelfeldt H 1999 J. Chem. Phys. 110 10235
Google Scholar
[3] Wunderlich C, Figger H, Hänsch T W 1996 Chem. Phys. Lett. 256 43
Google Scholar
[4] Ohmura H, Saito N, Morishita T 2014 Phys. Rev. A 89 013405
Google Scholar
[5] Trump C, Rottke H, Wittmann M, Korn G, Sandner W, Lein M, Engel V 2000 Phys. Rev. A 62 063402
Google Scholar
[6] Rottke H, Trump C, Wittmann M, et al. 2002 Phys. Rev. Lett. 89 013001
Google Scholar
[7] Kling M F, Siedschlag C, Znakovskaya I, Verhoef A J, Zherebtsov S, Krausz F, Lezius M, Vrakking M J J 2008 Mol. Phys. 106 455
Google Scholar
[8] Förster J, Vanne Y V, Saenz A 2014 Phys. Rev. A 90 053424
[9] Zhang X C, Shkurinov A, Zhang Y 2017 Nat. Photonics 11 16
Google Scholar
[10] Hafez H A, Chai X, Ibrahim A, Mondal S, Férachou D, Ropagnol X, Ozaki T 2016 J. Opt. 18 093004
Google Scholar
[11] Shaik S, Mandal D, Ramanan R 2016 Nat. Chem. 8 1091
Google Scholar
[12] Zeng Y, Zhou C, Song L, Lu X, Li Z, Ding Y, Bai Y, Xu Y, Leng Y, Tian Y, Liu J, Li R, Xu Z 2020 45th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz) Buffalo, New York, USA, November 8–13 2020 p1
[13] Kampfrath T, Tanaka K, Nelson K A 2013 Nat. Photonics 7 680
Google Scholar
[14] Salumbides E J, Dickenson G D, Ivanov T I, Ubachs W 2011 Phys. Rev. Lett. 107 043005
Google Scholar
[15] Dickenson G D, Niu M L, Salumbides E J, Komasa J, Eikema K S, Pachucki K, Ubachs W 2013 Phys. Rev. Lett. 110 193601
Google Scholar
[16] Liu J J, Salumbides E J, Hollenstein U, Koelemeij J C J, Eikema K S E, Ubachs W, Merkt F 2009 J. Chem. Phys. 130 174306
Google Scholar
[17] Saenz A 2000 Phys. Rev. A 61 051402
[18] Puchalski M, Komasa J, Pachucki K 2017 Phys. Rev. A 95 052506
Google Scholar
[19] Šmydke J, Ajay J, Remacle F, Levine R D 2017 Electronic and Nuclear Dynamics for a Non-Equilibrium Electronic State: The Ultrafast Pumping of N2 // Tadjer A, Pavlov R, Maruani J, Brändas E J, Delgado-Barrio G 2017 Quantum Systems in Physics, Chemistry, and Biology: Advances in Concepts and Applications (Vol. 30) (Cham: Springer International Publishing AG) p195
[20] Calvert C R, Bryan W A, Newell W R, Williams I D 2010 Phys. Rep. 491 1
Google Scholar
[21] Neese F 2011 Wiley Interdiscip. Rev. Comput. Mol. Sci. 2 73
Google Scholar
[22] Becerril R, Guzman F S, Rendon-Romero A, Valdez-Alvarado S 2008 Rev. Mex. Fis. E 54 120
[23] Wang K C, Yang L X, Wang S M, Guo L H, Ma J L, Tang J C, Bo W F, Wu Z, Zeng B Q, Gong Y B 2020 Phys. Chem. Chem. Phys. 22 9316
Google Scholar
[24] Neese F 2017 Wiley Interdiscip. Rev. Comput. Mol. Sci. 8 1
Google Scholar
[25] Stephens P J, Devlin F J, Chabalowski C F, Frisch M J 1994 J. Phys. Chem. 98 11623
Google Scholar
[26] Weigend F, Ahlrichs R 2005 Phys. Chem. Chem. Phys. 7 3297
Google Scholar
[27] Goerigk L, Grimme S 2011 J. Chem. Theory Comput. 7 291
Google Scholar
[28] Caldeweyher E, Bannwarth C, Grimme S 2017 J. Chem. Phys. 147 034112
Google Scholar
[29] Caldeweyher E, Ehlert S, Hansen A, Neugebauer H, Spicher S, Bannwarth C, Grimme S 2019 J. Chem. Phys. 150 154122
Google Scholar
[30] Cohen-Tannoudji C, Diu B, Laloë F 2019 Quantum Mechanics, Volume 1: Basic Concepts, Tools, and Applications (Vol. 1, 2nd Ed.) (New Jersey: John Wiley & Sons) p529
[31] Valkunas L, Abramavicius D, Mancal T 2013 Molecular Excitation Dynamics and Relaxation: Quantum Theory and Spectroscopy (New Jersey: John Wiley & Sons) p280
[32] Swope W C, Andersen H C, Berens P H, Wilson K R 1982 J. Chem. Phys. 76 637
Google Scholar
[33] 刘成卜, 邓从豪 1985 山东大学学报(自然科学版) 2 104
Liu C B, Deng C H 1985 Journal of Shandong University (Natural Science Edition) 2 104
-
图 1 氢分子的计算模型(球体表示氢原子), 两个氢核的连线平行于z轴
Figure 1. Calculation model of hydrogen molecules (spheres represent hydrogen atoms), two hydrogen nuclei are parallel to the z axis.
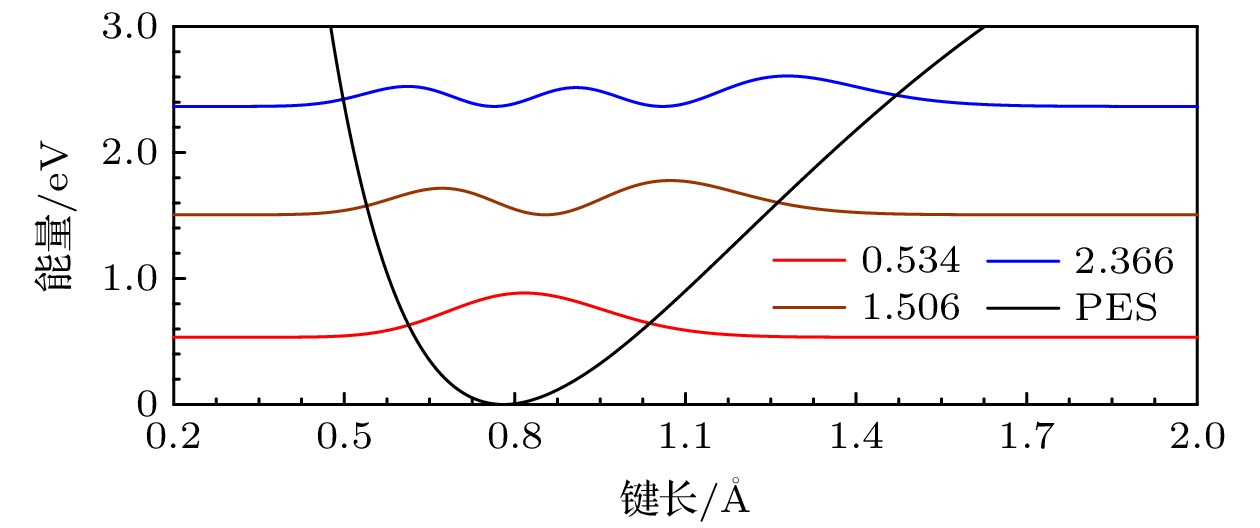
图 2 无外加电场时氢分子势能面(黑色曲线)及各能级概率密度分布曲线(彩色曲线), 氢分子的前3个本征振动模式由3条彩色曲线表示, 图例的数字代表氢分子每个本征模的能量E, 这里将势能面最低点设置为0
Figure 2. Without external electric field, the potential energy surface of hydrogen molecule (black curve) and the probability density distribution curve of each energy level (color curves). The first three eigen vibration modes of hydrogen molecule are represented by three color curves, the number in the legend represents the energy of each eigenmode of the hydrogen molecule, and the lowest point of potential energy surface is set to 0.
图 3 氢分子的势能面随外加电场强度与键长的变化图. 这幅图是用三次样条插值方法绘制, 颜色块代表能量, 单位是eV. 在电场强度增加至45 GV/m附近时, 最小势能点发生移动, 新的最小势能点出现在2.8 Å附近. 为了更清楚地展示势能面, 大于5 eV的体系势能用深红色表示
Figure 3. Variation of potential energy surface of hydrogen molecule with applied electric field intensity and bond length. This map is drawn by cubic spline interpolation method. The color block represents energy in eV. When the electric field intensity increases to 45 GV/m, the minimum potential energy point moves, and the new minimum energy point appears near 2.8 Å. In order to show the potential energy surface more clearly, the potential energy of the system greater than 5 eV is expressed in dark red.
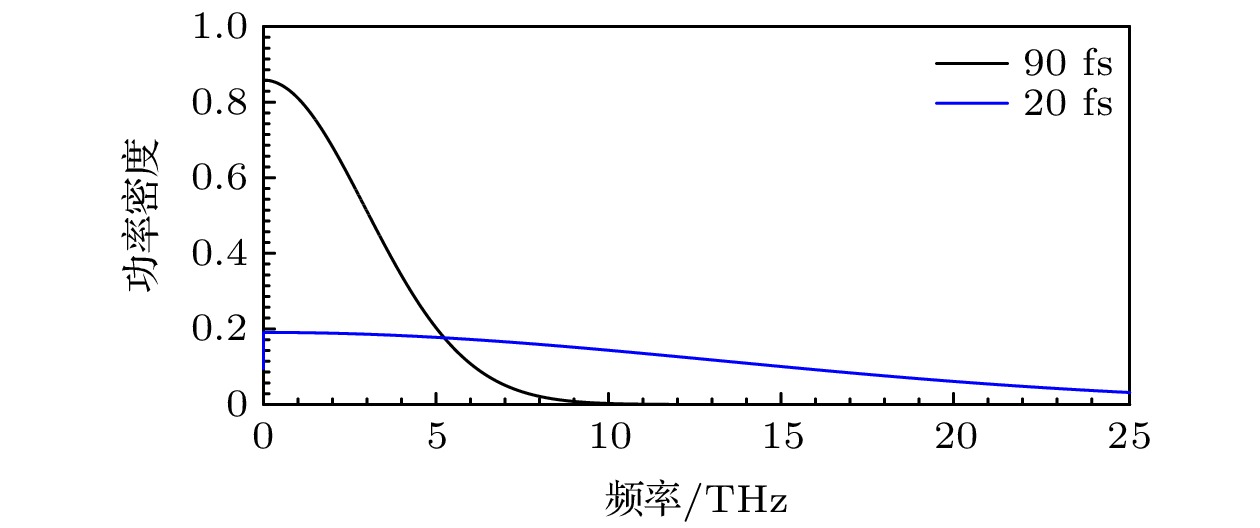
图 4 本文计算所使用的4个太赫兹高斯脉冲场的波形图, 幅值分别为35 GV/m (红色、紫色线)和60 GV/m (蓝色、黑色线), 脉宽分别为90 fs (红色、蓝色线)和20 fs (紫色、黑色线)
Figure 4. Waveforms of four THz pulse fields are calculated, the amplitudes are 35 GV/m (red, purple lines), 60 GV/m (blue, black lines), pulse width are 90 fs (red, blue lines), 20 fs (purple, black lines).
图 5 脉宽为90与20 fs的太赫兹脉冲波经傅里叶变换后的频谱图, 纵轴代表归一化的功率密度
Figure 5. Spectrum of THz pulse waves with 90 fs and 20 fs pulse width after fast Fourier transform. The longitudinal axis represents normalized power density.
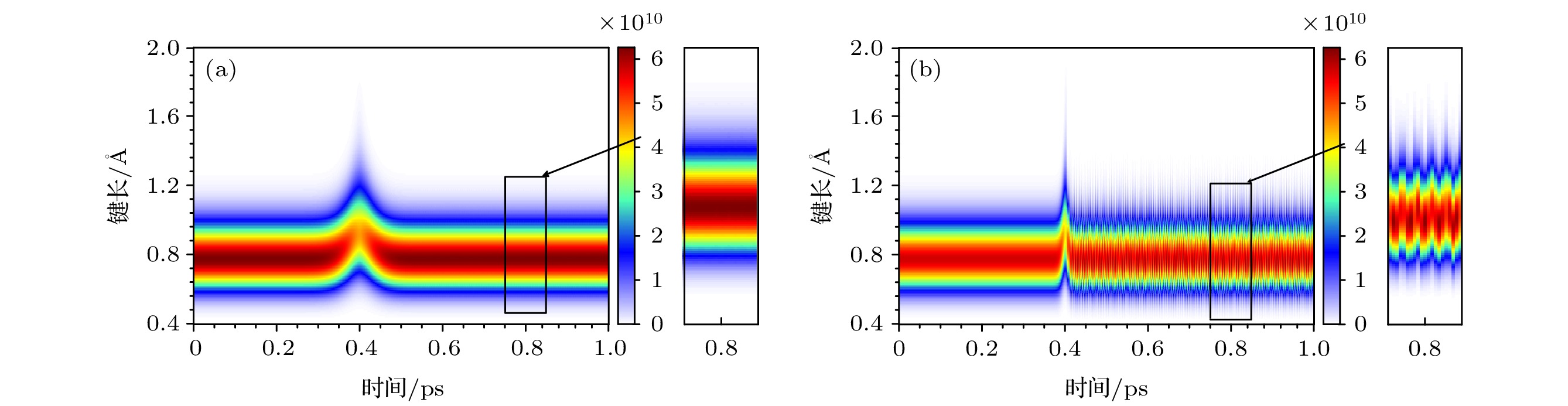
图 6 氢分子在幅值为35 GV/m的z方向高斯定向强场作用下质子概率密度分布的演化图, 施加的高斯脉冲电场的脉宽分别为(a) 90 fs与(b) 20 fs, 高斯脉冲中心设置在0.4 ps, 颜色条代表质子概率密度
Figure 6. Evolution diagram of proton probability density distribution of hydrogen molecule under the action of Gaussian directional intense field in z direction with amplitude of 35 GV/m. The pulse widths of applied Gaussian pulse electric field are (a) 90 fs and (b) 20 fs, respectively. The Gaussian pulse center is set at 0.4 ps, and the color strip represents the proton probability density.
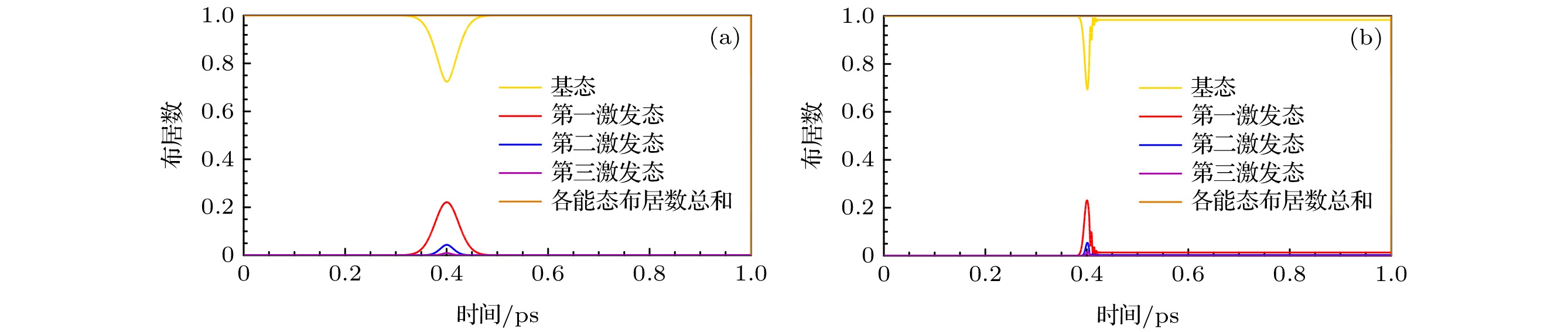
图 7 氢分子在幅值为35 GV/m的z方向高斯定向强场作用下能级布居数分布的演化图, 施加的高斯脉冲电场的脉宽分别为(a) 90 fs与(b) 20 fs, 高斯脉冲中心设置在0.4 ps, 不同颜色的曲线代表不同能级的布居数
Figure 7. Evolution diagram of the energy level population distribution of hydrogen molecule under the action of the Gaussian directional intense field in the z direction with the amplitude of 35 GV/m. The pulse widths of the applied Gaussian pulse electric field are (a) 90 fs and (b) 20 fs, respectively. The Gaussian pulse center is set at 0.4 ps. Curves of different colors represent populations of different energy levels.
图 8 氢分子在幅值为60 GV/m的z方向高斯定向强场作用下质子概率密度分布的演化图, 施加的高斯脉冲电场的脉宽分别为(a) 90 fs与(b) 20 fs, 高斯脉冲中心设置在0.4 ps, 颜色条代表质子概率密度
Figure 8. Evolution diagram of proton probability density distribution of hydrogen molecule under the action of Gaussian directional intense field in z direction with amplitude of 60 GV/m. The pulse widths of applied Gaussian pulse electric field are (a) 90 fs and (b) 20 fs, respectively. The Gaussian pulse center is set at 0.4 ps, and the color strip represents the proton probability density.
图 9 氢分子在幅值为60 GV/m的z方向高斯定向强场作用下能级布居数分布的演化图, 施加的高斯脉冲电场的脉宽分别为(a) 90 fs与(b) 20 fs, 高斯脉冲中心设置在0.4 ps, 不同颜色的曲线代表不同能级的布居数
Figure 9. Evolution diagram of the energy level population distribution of hydrogen molecule under the action of the Gaussian directional strong field in the z direction with the amplitude of 60 GV/m. The pulse widths of the applied Gaussian pulse electric field are (a) 90 fs and (b) 20 fs, respectively. The Gaussian pulse center is set at 0.4 ps. Curves of different colors represent populations of different energy levels
-
[1] Stapelfeldt H 2003 Eur. Phys. J. D 26 15
Google Scholar
[2] Sakai H, Safvan C P, Larsen J J, Hilligsoe K M, Hald K, Stapelfeldt H 1999 J. Chem. Phys. 110 10235
Google Scholar
[3] Wunderlich C, Figger H, Hänsch T W 1996 Chem. Phys. Lett. 256 43
Google Scholar
[4] Ohmura H, Saito N, Morishita T 2014 Phys. Rev. A 89 013405
Google Scholar
[5] Trump C, Rottke H, Wittmann M, Korn G, Sandner W, Lein M, Engel V 2000 Phys. Rev. A 62 063402
Google Scholar
[6] Rottke H, Trump C, Wittmann M, et al. 2002 Phys. Rev. Lett. 89 013001
Google Scholar
[7] Kling M F, Siedschlag C, Znakovskaya I, Verhoef A J, Zherebtsov S, Krausz F, Lezius M, Vrakking M J J 2008 Mol. Phys. 106 455
Google Scholar
[8] Förster J, Vanne Y V, Saenz A 2014 Phys. Rev. A 90 053424
[9] Zhang X C, Shkurinov A, Zhang Y 2017 Nat. Photonics 11 16
Google Scholar
[10] Hafez H A, Chai X, Ibrahim A, Mondal S, Férachou D, Ropagnol X, Ozaki T 2016 J. Opt. 18 093004
Google Scholar
[11] Shaik S, Mandal D, Ramanan R 2016 Nat. Chem. 8 1091
Google Scholar
[12] Zeng Y, Zhou C, Song L, Lu X, Li Z, Ding Y, Bai Y, Xu Y, Leng Y, Tian Y, Liu J, Li R, Xu Z 2020 45th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz) Buffalo, New York, USA, November 8–13 2020 p1
[13] Kampfrath T, Tanaka K, Nelson K A 2013 Nat. Photonics 7 680
Google Scholar
[14] Salumbides E J, Dickenson G D, Ivanov T I, Ubachs W 2011 Phys. Rev. Lett. 107 043005
Google Scholar
[15] Dickenson G D, Niu M L, Salumbides E J, Komasa J, Eikema K S, Pachucki K, Ubachs W 2013 Phys. Rev. Lett. 110 193601
Google Scholar
[16] Liu J J, Salumbides E J, Hollenstein U, Koelemeij J C J, Eikema K S E, Ubachs W, Merkt F 2009 J. Chem. Phys. 130 174306
Google Scholar
[17] Saenz A 2000 Phys. Rev. A 61 051402
[18] Puchalski M, Komasa J, Pachucki K 2017 Phys. Rev. A 95 052506
Google Scholar
[19] Šmydke J, Ajay J, Remacle F, Levine R D 2017 Electronic and Nuclear Dynamics for a Non-Equilibrium Electronic State: The Ultrafast Pumping of N2 // Tadjer A, Pavlov R, Maruani J, Brändas E J, Delgado-Barrio G 2017 Quantum Systems in Physics, Chemistry, and Biology: Advances in Concepts and Applications (Vol. 30) (Cham: Springer International Publishing AG) p195
[20] Calvert C R, Bryan W A, Newell W R, Williams I D 2010 Phys. Rep. 491 1
Google Scholar
[21] Neese F 2011 Wiley Interdiscip. Rev. Comput. Mol. Sci. 2 73
Google Scholar
[22] Becerril R, Guzman F S, Rendon-Romero A, Valdez-Alvarado S 2008 Rev. Mex. Fis. E 54 120
[23] Wang K C, Yang L X, Wang S M, Guo L H, Ma J L, Tang J C, Bo W F, Wu Z, Zeng B Q, Gong Y B 2020 Phys. Chem. Chem. Phys. 22 9316
Google Scholar
[24] Neese F 2017 Wiley Interdiscip. Rev. Comput. Mol. Sci. 8 1
Google Scholar
[25] Stephens P J, Devlin F J, Chabalowski C F, Frisch M J 1994 J. Phys. Chem. 98 11623
Google Scholar
[26] Weigend F, Ahlrichs R 2005 Phys. Chem. Chem. Phys. 7 3297
Google Scholar
[27] Goerigk L, Grimme S 2011 J. Chem. Theory Comput. 7 291
Google Scholar
[28] Caldeweyher E, Bannwarth C, Grimme S 2017 J. Chem. Phys. 147 034112
Google Scholar
[29] Caldeweyher E, Ehlert S, Hansen A, Neugebauer H, Spicher S, Bannwarth C, Grimme S 2019 J. Chem. Phys. 150 154122
Google Scholar
[30] Cohen-Tannoudji C, Diu B, Laloë F 2019 Quantum Mechanics, Volume 1: Basic Concepts, Tools, and Applications (Vol. 1, 2nd Ed.) (New Jersey: John Wiley & Sons) p529
[31] Valkunas L, Abramavicius D, Mancal T 2013 Molecular Excitation Dynamics and Relaxation: Quantum Theory and Spectroscopy (New Jersey: John Wiley & Sons) p280
[32] Swope W C, Andersen H C, Berens P H, Wilson K R 1982 J. Chem. Phys. 76 637
Google Scholar
[33] 刘成卜, 邓从豪 1985 山东大学学报(自然科学版) 2 104
Liu C B, Deng C H 1985 Journal of Shandong University (Natural Science Edition) 2 104
DownLoad:
Catalog
Metrics
- Abstract views: 5642
- PDF Downloads: 125
- Cited By: 0
