-
Owing to the low energy density of sound energy in nature, it is difficult to realize the local enhancement effect of sound field in air. Therefore, it is of great significance to explore new physical mechanisms and methods to achieve sound field enhancement. In recent years, artificial Mie resonance structure as a kind of acoustic metamaterial has attracted considerable attention, which has a variety of resonant modes, such as monopolar, dipolar, quadrupolar and higher multipolar modes. Compared with local resonance, acoustic Mie resonance mode has strong acoustic interaction, which can effectively enhance the acoustic field by the coupling of the Mie resonance. In this paper, we design an acoustic metamaterial composed of multiple-cavity unit cells, which is capable of realizing sound field enhancement. The multiple-cavity unit is circular in external shape and it is composed of a circular central cavity and twelve resonators. The twelve resonators are evenly distributed around the circular central cavity, with three resonators combined into a group. This exotic function arises from the compound monopole Mie resonance introduced by mutual coupling between the system structure and the monopole Mie resonance of each unit cell. Symmetric and asymmetric metamaterials are constructed by arranging several multiple-cavity unit cells in different forms. These two kinds of metamaterials can be used to achieve sound field enhancement with different effects. The results show that due to the symmetry of metamaterial structure, the symmetric metamaterials with square, circle, rectangle and regular hexagon shapes can realize the sound field enhancement, which is independent of the direction of incident wave. However, for the asymmetric metamaterial with equilateral triangle shape, the sound intensity in the center of the system varies with incident direction, which indicates that the designed asymmetric metamaterial has a strong dependence on the direction of incident wave. These two kinds of metamaterials constructed in this research can possess a number of potential applications such as in sound insulation, acoustic sensor, noise location, acoustic communication and asymmetric acoustic device. These two kinds of metamaterials constructed in this research can possess a number of potential applications such as in sound insulation.
-
Keywords:
- Mie resonance /
- symmetric metamaterial /
- asymmetric metamaterial /
- sound field enhancement
[1] Liu Z Y, Zhang X X, Mao Y W, Zhu Y Y, Yang Z Y, Chan C T, Sheng P 2000 Science 289 1734
Google Scholar
[2] Fang N, Xi D, Xu J, Ambati M, Srituravanich W, Sun C, Zhang X 2006 Nat. Mater. 5 452
Google Scholar
[3] Yang Z, Mei J, Yang M, Chan N H, Sheng P 2008 Phys. Rev. Lett. 101 204301
Google Scholar
[4] Liang Z, Li J 2012 Phys. Rev. Lett. 108 114301
Google Scholar
[5] Ma G, Sheng P 2016 Sci. Adv. 2 e1501595
Google Scholar
[6] Cummer S A, Christensen J, Alu A 2016 Nat. Rev. Mater. 1 16001
Google Scholar
[7] Liu F, Phipps A, Horowitz S, Ngo K, Cattafesta L, Nishida T, Sheplak M, 2008 J. Acoust. Soc. Am. 123 1983
Google Scholar
[8] Li B, Laviage J A, You J H, Kim Y J 2013 Appl. Acoust. 74 1271
Google Scholar
[9] Li B, You J H, Kim Y J 2013 Smart Mater. Struct. 22 055013
Google Scholar
[10] Yuan M, Cao Z, Luo J, Zhang J, Chang C 2017 Sensor. Actuat. A-Phys. 264 84
Google Scholar
[11] Yuan M, Cao Z, Luo J, Pang Z 2018 AIP Adv. 8 085012
Google Scholar
[12] Song K, Lee S H, Kim K, Hur S, Kim J 2014 Sci. Rep. 4 4165
Google Scholar
[13] Zhu X, Liang B, Kan W, Peng Y, Cheng J 2016 Phys. Rev. Appl. 5 054015
Google Scholar
[14] Zhao J, Zhang L, Wu Y 2017 J. Acoust. Soc. Am. 142 4990010
Google Scholar
[15] Shen C, Li J F, Jia Z T, Xie Y B, Cummer S A 2019 Phys. Rev. B 99 134306
Google Scholar
[16] Li J F, Shen C, Zhu X H, Xie Y B, Cummer S A 2019 Phys. Rev. B 99 144311
Google Scholar
[17] Fu Y Y, Shen C, Cao Y Y, Gao L, Chen H Y, Chan C T, Cummer S A, Xu Y D 2019 Nat. Commun. 10 2326
Google Scholar
[18] Jin M, Liang B, Yang J, Yang J, Cheng J C 2019 Sci. Rep. 9 11152
Google Scholar
[19] Liang B, Yuan B, Cheng J C 2009 Phys. Rev. Lett. 103 104301
Google Scholar
[20] Liu F M, Huang X Q, Chan C T 2012 Appl. Phys. Lett. 100 071911
Google Scholar
[21] Jing Y, Xu J, Fang N X 2012 Phys. Lett. A 376 2834
Google Scholar
[22] Li Y, Liang B, Gu Z M, Zou X Y, Cheng J C 2013 Appl. Phys. Lett. 103 053505
Google Scholar
[23] Shen C, Xie Y B, Li J F, Cummer S A, Yun J 2016 Appl. Phys. Lett. 108 223502
Google Scholar
[24] Song X P, Chen T N, Zhu J, Ding W, Liang Q X, Wang X P 2020 Phys. Lett. A 384 126419
Google Scholar
[25] Lu G X, Ding E L, Wang Y Y, Peng X Y, Cui J, Liu X Z, Liu X J 2017 Appl. Phys. Lett. 110 123507
Google Scholar
[26] Vladimir F, Muralidhar A, Sun C, Zhang X 2007 Phys. Rev. B 76 144302
Google Scholar
[27] Gao W T, Xia J P, Sun H X, Yuan S Q, Ge Y, Liu X J 2019 Appl. Phys. Express 12 044002
Google Scholar
-
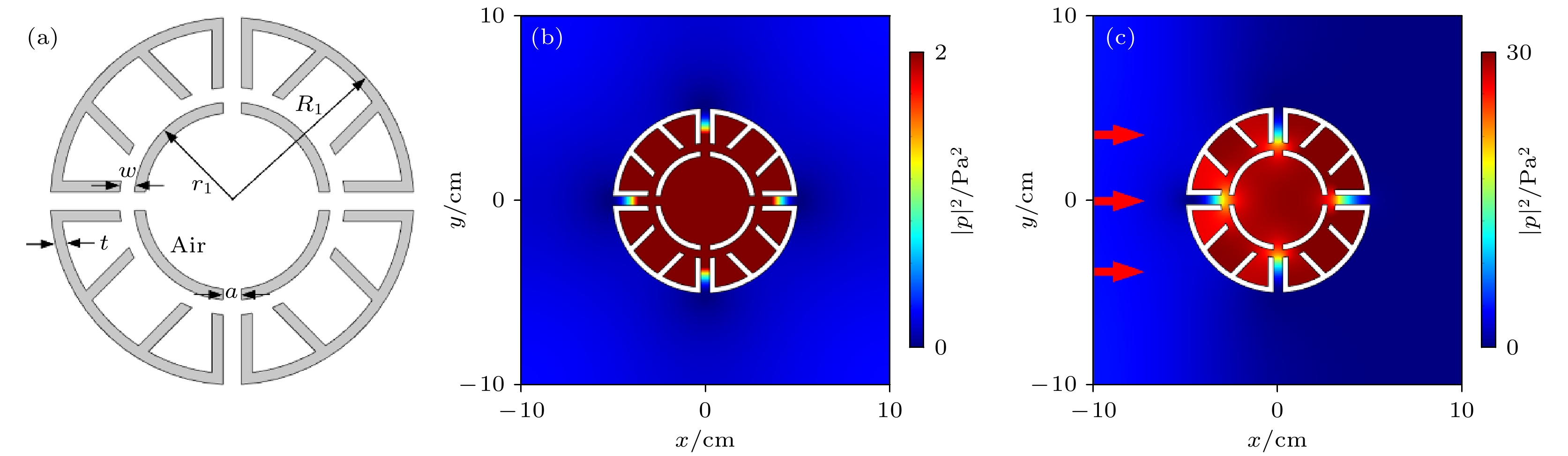
图 1 (a)多腔型基本单元的结构示意图; (b)特征频率为672 Hz时, 基本单元在单极子Mie共振模式下的声强分布图; (c)当频率为672 Hz的声波从结构左侧垂直入射时, 多腔型基本单元的声强分布图
Figure 1. (a) Structural diagram of multiple-cavity unit; (b) sound intensity distribution of the unit in monopole Mie resonance mode at the characteristic frequency of 672 Hz; (c) sound intensity distribution of the unit when the sound wave with frequency of 672 Hz is normally incident from the left side.
图 2 (a)由8个多腔型基本单元组成的正方形系统示意图; (b)特征频率为669 Hz时, 正方形系统在复合单极子Mie共振模式下的声强分布图
Figure 2. (a) Schematic diagram of a square system composed of eight multiple-cavity units; (b) sound intensity distribution of the square system in the compound monopole Mie resonance mode at the characteristic frequency of 669 Hz.
图 3 声波从(a)左侧和(b)右侧垂直入射到8个多腔型基本单元组成的正方形系统时的声强分布图; (c)声波从左侧垂直入射到由8个硬边界圆形结构组成的系统时的声强分布
Figure 3. Sound intensity distributions of the square system composed of eight multiple-cavity units when the sound wave is normally incident from (a) the left side and (b) the right side, respectively; (c) sound intensity distribution of the system composed of eight hard boundary circular structures when the sound wave is normally incident from the left side.
图 4 由多腔型基本单元组成的(a)圆形、(b)矩形和(c)正六边形对称型超构材料的结构示意图; 在复合单极子Mie共振模式下, (d)圆形超构材料、(e)矩形超构材料和(f)正六边形超构材料的声强分布图, 对应的工作频率分别为648, 629, 621 Hz
Figure 4. Schematic diagram of the (a) circular, (b) rectangular and (c) regular hexagonal symmetric metamaterials composed of multiple-cavity units. Sound intensity distributions of the (d) circular metamaterial, (e) rectangular metamaterial and (f) regular hexagonal metamaterial under the compound monopole Mie resonance mode with the working frequencies of 648, 629 and 621 Hz, respectively.
图 5 (a) 6个多腔型基本单元组成的等边三角形非对称型超构材料的结构示意图; (b) 当频率为637 Hz的声波从结构左侧垂直入射时, 非对称超构材料的声强分布图; (c) 非对称超构材料内部点A处的声强随入射声波角度的变化情况; (d) 当频率为637 Hz的声波从结构右侧垂直入射时, 非对称超构材料的声强分布图
Figure 5. (a) Structural diagram of the equilateral triangular asymmetric metamaterial composed of six multiple-cavity units; (b) sound intensity distribution of the asymmetric metamaterial when the sound wave with frequency of 637 Hz is normally incident from the left side; (c) acoustic intensity curve at the center point A of the asymmetric metamaterial with different angles of incident wave; (d) sound intensity distribution of the asymmetric metamaterial when the sound wave is normally incident from the right side with frequency of 637 Hz.
-
[1] Liu Z Y, Zhang X X, Mao Y W, Zhu Y Y, Yang Z Y, Chan C T, Sheng P 2000 Science 289 1734
Google Scholar
[2] Fang N, Xi D, Xu J, Ambati M, Srituravanich W, Sun C, Zhang X 2006 Nat. Mater. 5 452
Google Scholar
[3] Yang Z, Mei J, Yang M, Chan N H, Sheng P 2008 Phys. Rev. Lett. 101 204301
Google Scholar
[4] Liang Z, Li J 2012 Phys. Rev. Lett. 108 114301
Google Scholar
[5] Ma G, Sheng P 2016 Sci. Adv. 2 e1501595
Google Scholar
[6] Cummer S A, Christensen J, Alu A 2016 Nat. Rev. Mater. 1 16001
Google Scholar
[7] Liu F, Phipps A, Horowitz S, Ngo K, Cattafesta L, Nishida T, Sheplak M, 2008 J. Acoust. Soc. Am. 123 1983
Google Scholar
[8] Li B, Laviage J A, You J H, Kim Y J 2013 Appl. Acoust. 74 1271
Google Scholar
[9] Li B, You J H, Kim Y J 2013 Smart Mater. Struct. 22 055013
Google Scholar
[10] Yuan M, Cao Z, Luo J, Zhang J, Chang C 2017 Sensor. Actuat. A-Phys. 264 84
Google Scholar
[11] Yuan M, Cao Z, Luo J, Pang Z 2018 AIP Adv. 8 085012
Google Scholar
[12] Song K, Lee S H, Kim K, Hur S, Kim J 2014 Sci. Rep. 4 4165
Google Scholar
[13] Zhu X, Liang B, Kan W, Peng Y, Cheng J 2016 Phys. Rev. Appl. 5 054015
Google Scholar
[14] Zhao J, Zhang L, Wu Y 2017 J. Acoust. Soc. Am. 142 4990010
Google Scholar
[15] Shen C, Li J F, Jia Z T, Xie Y B, Cummer S A 2019 Phys. Rev. B 99 134306
Google Scholar
[16] Li J F, Shen C, Zhu X H, Xie Y B, Cummer S A 2019 Phys. Rev. B 99 144311
Google Scholar
[17] Fu Y Y, Shen C, Cao Y Y, Gao L, Chen H Y, Chan C T, Cummer S A, Xu Y D 2019 Nat. Commun. 10 2326
Google Scholar
[18] Jin M, Liang B, Yang J, Yang J, Cheng J C 2019 Sci. Rep. 9 11152
Google Scholar
[19] Liang B, Yuan B, Cheng J C 2009 Phys. Rev. Lett. 103 104301
Google Scholar
[20] Liu F M, Huang X Q, Chan C T 2012 Appl. Phys. Lett. 100 071911
Google Scholar
[21] Jing Y, Xu J, Fang N X 2012 Phys. Lett. A 376 2834
Google Scholar
[22] Li Y, Liang B, Gu Z M, Zou X Y, Cheng J C 2013 Appl. Phys. Lett. 103 053505
Google Scholar
[23] Shen C, Xie Y B, Li J F, Cummer S A, Yun J 2016 Appl. Phys. Lett. 108 223502
Google Scholar
[24] Song X P, Chen T N, Zhu J, Ding W, Liang Q X, Wang X P 2020 Phys. Lett. A 384 126419
Google Scholar
[25] Lu G X, Ding E L, Wang Y Y, Peng X Y, Cui J, Liu X Z, Liu X J 2017 Appl. Phys. Lett. 110 123507
Google Scholar
[26] Vladimir F, Muralidhar A, Sun C, Zhang X 2007 Phys. Rev. B 76 144302
Google Scholar
[27] Gao W T, Xia J P, Sun H X, Yuan S Q, Ge Y, Liu X J 2019 Appl. Phys. Express 12 044002
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 5523
- PDF Downloads: 154
- Cited By: 0
