-
In this paper, we numerically investigate the late-time growth of high-Reynolds-number single-mode Rayleigh-Taylor instability in a long pipe by using an advanced phase-field lattice Boltzmann multiphase method. We mainly analyze the influence of surface tension on interfacial dynamic behavior and the development of the bubble front and spike front. The numerical experiments indicate that increasing surface tension can significantly reduce the complexity of formed interfacial structure and also prevents the breakup of phase interfaces. The interface patterns in the instability process cannot always preserve the symmetric property under the extremely small surface tension, but they do maintain the symmetries with respect to the middle line as the surface tension is increased. We also report that the bubble amplitude first increases then decreases with the surface tension. There are no obvious differences between the curves of spike amplitudes for low surface tensions. However, when the surface tension increases to a critical value, it can slow down the spike growth significantly. When the surface tension is lower than the critical value, the development of the high-Reynolds-number Rayleigh-Taylor instability can be divided into four different stages, i.e. the linear growth, saturated velocity growth, reacceleration, and chaotic mixing. The bubble and spike velocities at the second stage show good agreement with those from the modified potential flow theory that takes the surface tension effect into account. After that, the bubble front and spike front are accelerated due to the formation of Kelvin-Helmholtz vortices in the interfacial region. At the late time, the bubble velocity and spike velocity become unstable and slightly fluctuate over time. To determine the nature of the late-time growth, we also measure the bubble and spike normalized accelerations at various interfacial tensions and Atwood numbers. It is found that both the spike and bubble growth rates first increase then decrease with the surface tension in general. Finally, we deduce a theoretical formula for the critical surface tension, below which the Rayleigh-Taylor instability takes place and above which tension it does not occur. It is shown that the critical surface tension increases with the Atwood number and also the numerical predictions by the lattice Boltzmann method are also in accord well with the theoretical results.
-
Keywords:
- Rayleigh-Taylor instability /
- lattice Boltzmann method /
- surface tension /
- late-time growth /
- critical value
[1] Zhou Y 2017 Phys. Rep. 720–722 1
Google Scholar
[2] Rayleigh L 1883 Proc. London Math. Soc. 14 170
[3] Taylor G I 1950 Proc. R. Soc. London, Ser. A 201 192
Google Scholar
[4] Lewis D J 1950 Proc. R. Soc. London, Ser. A 202 81
Google Scholar
[5] Sharp D H 1984 Physica D 12 3
Google Scholar
[6] Waddell J T, Niederhaus C E, Jacobs J W 2001 Phys. Fluids 13 1263
Google Scholar
[7] Glimm J, Li X L, Lin A D 2002 Acta Math. Appl. Sin. 18 1
[8] Wilkinson J P, Jacobs J W 2007 Phys. Fluids 19 124102
Google Scholar
[9] Goncharov V N 2002 Phys. Rev. Lett. 88 134502
Google Scholar
[10] Ramaprabhu P, Dimonte G, Woodward P, Fryer C, Rockefeller G, Muthuraman K, Lin P H, Jayaral J 2012 Phys. Fluids 24 074107
Google Scholar
[11] Wei T, Livescu D 2012 Phys. Rev. E 86 046405
Google Scholar
[12] Lai H L, Xu A G, Zhang G, Gan Y B, Jun Y, Succi S 2016 Phys. Rev. E 94 023106
Google Scholar
[13] Liang H, Shi B C, Guo Z L, Chai Z H 2014 Phys. Rev. E 89 053320
Google Scholar
[14] Liang H, Li Q X, Shi B C, Chai Z H 2016 Phys. Rev. E 93 033113
Google Scholar
[15] 胡晓亮, 梁宏, 王会利 2020 69 044701
Google Scholar
Hu X L, Liang H, Wang H L 2020 Acta Phys. Sin. 69 044701
Google Scholar
[16] Sohn S I, Baek S 2017 Phys. Lett. A 381 3812
Google Scholar
[17] Cherfils C, Mikaelian K O 1996 Phys. Fluids 8 522
Google Scholar
[18] Dimonte G, Schneider M 2000 Phys. Fluids 12 304
Google Scholar
[19] Garnier J, Cherfils-Clérouin C, Holstein P A 2003 Phys. Rev. E 68 036401
Google Scholar
[20] Chertkov M, Kolokolov I, Lebedev V 2005 Phys. Rev. E 71 055301(R
Google Scholar
[21] Daly B J 1969 Phys. Fluids 12 1340
Google Scholar
[22] Zhang R Y, He X Y, Chen S Y 2000 Comput. Phys. Commun. 129 121
Google Scholar
[23] Young Y N, Ham F E 2006 J. Turbul. 7 71
Google Scholar
[24] Sohn S I 2009 Phys. Rev. E 80 055302(R
Google Scholar
[25] 夏同军, 董永强, 曹义刚 2013 62 214702
Google Scholar
Xia T J, Dong Y Q, Cao Y G 2013 Acta Phys. Sin. 62 214702
Google Scholar
[26] Zufiria J A 1988 Phys. Fluids 31 440
Google Scholar
[27] Li M J, Zhu Q F, Li G B 2016 Appl. Math. Mech. 37 1607
Google Scholar
[28] Guo H Y, Wang L F, Ye W H, Wu J F, Zhang W Y 2017 Chin. Phys. Lett. 34 045201
Google Scholar
[29] Guo Z L, Shu C 2013 Lattice Boltzmann Method and its Applications in Engineering (Singapore: World Scientific), pp239–284
[30] Wang H L, Yuan X L, Liang H, Chai Z H, Shi B C 2019 Capillarity 2 33
Google Scholar
[31] Liang H, Xu J R, Chen J X, Wang H L, Chai Z H, Shi B C 2018 Phys. Rev. E 97 033309
Google Scholar
[32] Liang H, Hu X L, Huang X F, Xu J R 2019 Phys. Fluids 31 112104
Google Scholar
[33] Jacqmin D 1999 J. Comput. Phys. 155 96
Google Scholar
[34] Wei Y K, Wang Z D, Dou H S, Qian Y H 2017 Comput. Fluids 156 97
Google Scholar
[35] Wei Y K, Yang H, Lin Z, Wang Z D, Qian Y H 2018 Appl. Math. Comput. 339 556
[36] Lallemand P, Luo L S 2000 Phys. Rev. E 61 6546
Google Scholar
[37] Chai Z H, Shi B C, Lu J H, Guo Z L 2010 Comput. Fluids 39 2069
Google Scholar
[38] Liang H, Shi B C, Chai Z H 2016 Phys. Rev. E 93 013308
Google Scholar
[39] He X, Zou Q, Luo L S, Dembo M 1997 J. Stat. Phys. 87 115
Google Scholar
[40] Bian X, Aluie H, Zhao D X, Zhang H S, Livescu D 2020 Physica D 403 132250
Google Scholar
[41] Cabot W H, Cook A W 2006 Nat. Phys. 2 562
Google Scholar
-
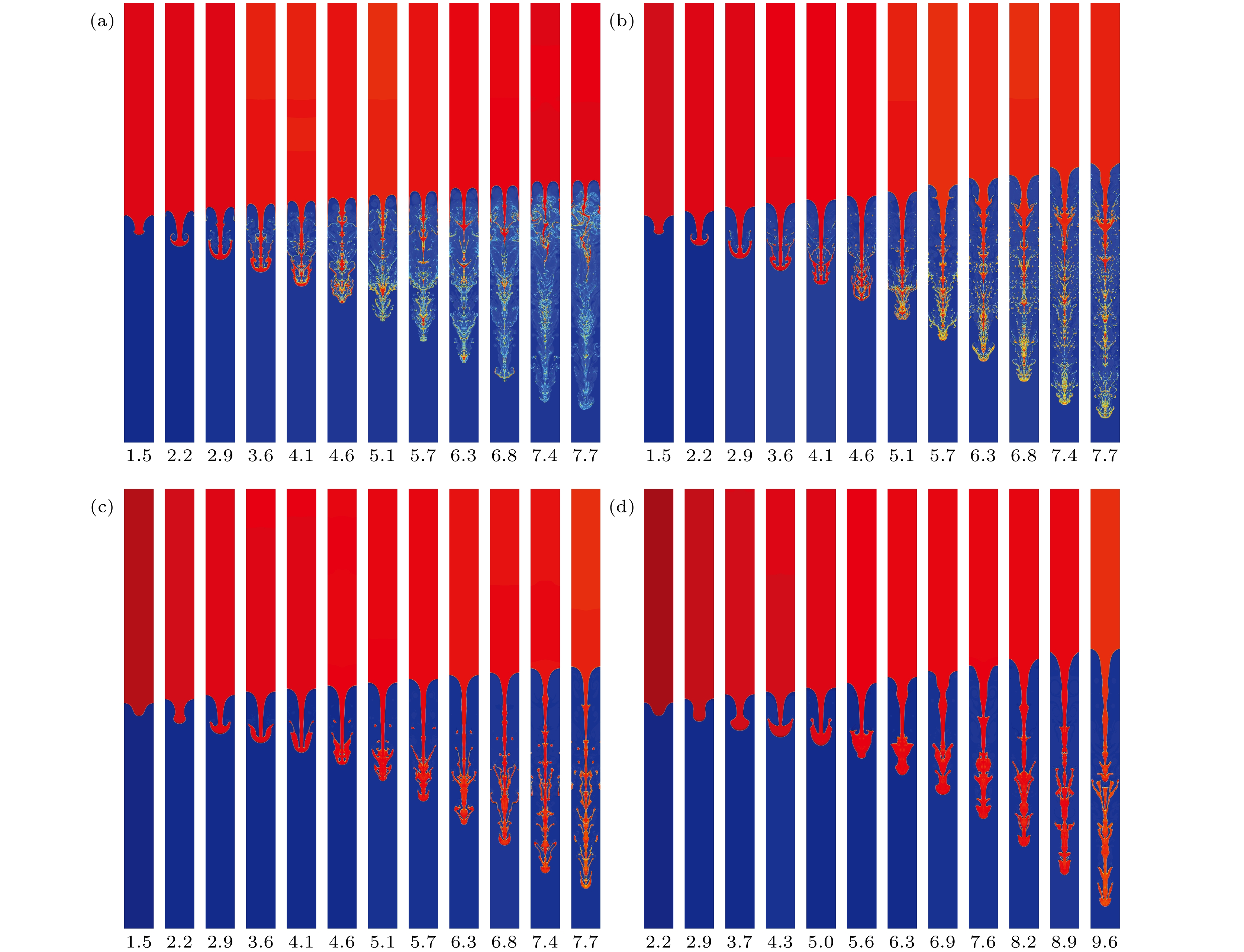
图 1
$ Re = 10^4 $ ,$ A_t = 0.7 $ 时, 表面张力对高雷诺数非混相RT不稳定相界面演化的影响 (a)$ \sigma = 5\times10^{-6} $ ; (b)$\sigma = $ $ 5\times10^{-4}$ ; (c)$ \sigma = 5\times10^{-3} $ ; (d)$ \sigma = 1\times10^{-2} $ Figure 1. Effect of the surface tension on the evolution of phase interface in the immiscible RT instability with
$ Re = 10^4 $ ,$ A_t = 0.7 $ : (a)$ \sigma = 5\times10^{-6} $ ; (b)$ \sigma = 5\times10^{-4} $ ; (c)$ \sigma = 5\times10^{-3} $ ; (d)$ \sigma = 1\times10^{-2} $ .
图 2 表面张力对随时间变化的气泡和尖钉振幅的影响
Figure 2. Influence of surface tension on the time variations of bubble and spike amplitudes.
图 3 表面张力对随时间演化的气泡和尖钉增长速度的影响. 蓝色和虚线分别表示势能模型预测气泡与尖钉速度在
$ \sigma = 5\times10^{-3} $ 和$ \sigma = 1\times10^{-2} $ 时的解析解Figure 3. Influence of surface tension on the time evolutions of bubble and spike growth velocities. The blue and yellow dotted lines represent the analytical solutions of the bubble and spike velocities from potential flow model at
$ \sigma = 5\times10^{-3} $ and$ \sigma = 1\times10^{-2} $ .
图 4 不同Atwood数下气泡与尖钉的后期增长率系数
$ \alpha_{\rm {b, s}} $ 随表面张力的变化Figure 4. Variations of bubble and spike late-time growth coefficients
$ \alpha_{\rm {b, s}} $ with respect to the surface tension under different Atwood numbers
图 5 不同 Atwood 数下的临界表面张力
Figure 5. Critical surface tensions at various Atwood numbers.
-
[1] Zhou Y 2017 Phys. Rep. 720–722 1
Google Scholar
[2] Rayleigh L 1883 Proc. London Math. Soc. 14 170
[3] Taylor G I 1950 Proc. R. Soc. London, Ser. A 201 192
Google Scholar
[4] Lewis D J 1950 Proc. R. Soc. London, Ser. A 202 81
Google Scholar
[5] Sharp D H 1984 Physica D 12 3
Google Scholar
[6] Waddell J T, Niederhaus C E, Jacobs J W 2001 Phys. Fluids 13 1263
Google Scholar
[7] Glimm J, Li X L, Lin A D 2002 Acta Math. Appl. Sin. 18 1
[8] Wilkinson J P, Jacobs J W 2007 Phys. Fluids 19 124102
Google Scholar
[9] Goncharov V N 2002 Phys. Rev. Lett. 88 134502
Google Scholar
[10] Ramaprabhu P, Dimonte G, Woodward P, Fryer C, Rockefeller G, Muthuraman K, Lin P H, Jayaral J 2012 Phys. Fluids 24 074107
Google Scholar
[11] Wei T, Livescu D 2012 Phys. Rev. E 86 046405
Google Scholar
[12] Lai H L, Xu A G, Zhang G, Gan Y B, Jun Y, Succi S 2016 Phys. Rev. E 94 023106
Google Scholar
[13] Liang H, Shi B C, Guo Z L, Chai Z H 2014 Phys. Rev. E 89 053320
Google Scholar
[14] Liang H, Li Q X, Shi B C, Chai Z H 2016 Phys. Rev. E 93 033113
Google Scholar
[15] 胡晓亮, 梁宏, 王会利 2020 69 044701
Google Scholar
Hu X L, Liang H, Wang H L 2020 Acta Phys. Sin. 69 044701
Google Scholar
[16] Sohn S I, Baek S 2017 Phys. Lett. A 381 3812
Google Scholar
[17] Cherfils C, Mikaelian K O 1996 Phys. Fluids 8 522
Google Scholar
[18] Dimonte G, Schneider M 2000 Phys. Fluids 12 304
Google Scholar
[19] Garnier J, Cherfils-Clérouin C, Holstein P A 2003 Phys. Rev. E 68 036401
Google Scholar
[20] Chertkov M, Kolokolov I, Lebedev V 2005 Phys. Rev. E 71 055301(R
Google Scholar
[21] Daly B J 1969 Phys. Fluids 12 1340
Google Scholar
[22] Zhang R Y, He X Y, Chen S Y 2000 Comput. Phys. Commun. 129 121
Google Scholar
[23] Young Y N, Ham F E 2006 J. Turbul. 7 71
Google Scholar
[24] Sohn S I 2009 Phys. Rev. E 80 055302(R
Google Scholar
[25] 夏同军, 董永强, 曹义刚 2013 62 214702
Google Scholar
Xia T J, Dong Y Q, Cao Y G 2013 Acta Phys. Sin. 62 214702
Google Scholar
[26] Zufiria J A 1988 Phys. Fluids 31 440
Google Scholar
[27] Li M J, Zhu Q F, Li G B 2016 Appl. Math. Mech. 37 1607
Google Scholar
[28] Guo H Y, Wang L F, Ye W H, Wu J F, Zhang W Y 2017 Chin. Phys. Lett. 34 045201
Google Scholar
[29] Guo Z L, Shu C 2013 Lattice Boltzmann Method and its Applications in Engineering (Singapore: World Scientific), pp239–284
[30] Wang H L, Yuan X L, Liang H, Chai Z H, Shi B C 2019 Capillarity 2 33
Google Scholar
[31] Liang H, Xu J R, Chen J X, Wang H L, Chai Z H, Shi B C 2018 Phys. Rev. E 97 033309
Google Scholar
[32] Liang H, Hu X L, Huang X F, Xu J R 2019 Phys. Fluids 31 112104
Google Scholar
[33] Jacqmin D 1999 J. Comput. Phys. 155 96
Google Scholar
[34] Wei Y K, Wang Z D, Dou H S, Qian Y H 2017 Comput. Fluids 156 97
Google Scholar
[35] Wei Y K, Yang H, Lin Z, Wang Z D, Qian Y H 2018 Appl. Math. Comput. 339 556
[36] Lallemand P, Luo L S 2000 Phys. Rev. E 61 6546
Google Scholar
[37] Chai Z H, Shi B C, Lu J H, Guo Z L 2010 Comput. Fluids 39 2069
Google Scholar
[38] Liang H, Shi B C, Chai Z H 2016 Phys. Rev. E 93 013308
Google Scholar
[39] He X, Zou Q, Luo L S, Dembo M 1997 J. Stat. Phys. 87 115
Google Scholar
[40] Bian X, Aluie H, Zhao D X, Zhang H S, Livescu D 2020 Physica D 403 132250
Google Scholar
[41] Cabot W H, Cook A W 2006 Nat. Phys. 2 562
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 5264
- PDF Downloads: 108
- Cited By: 0
