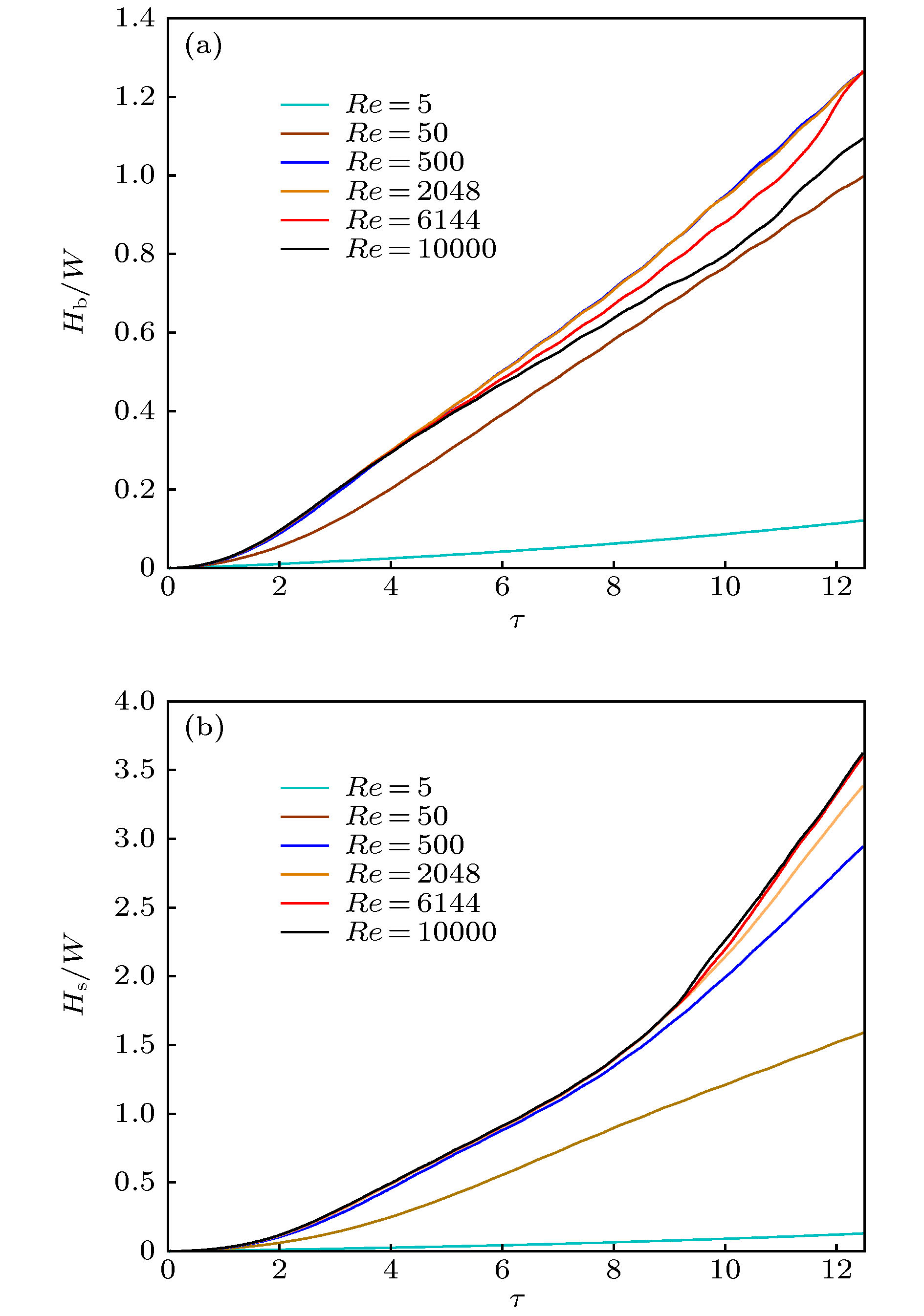
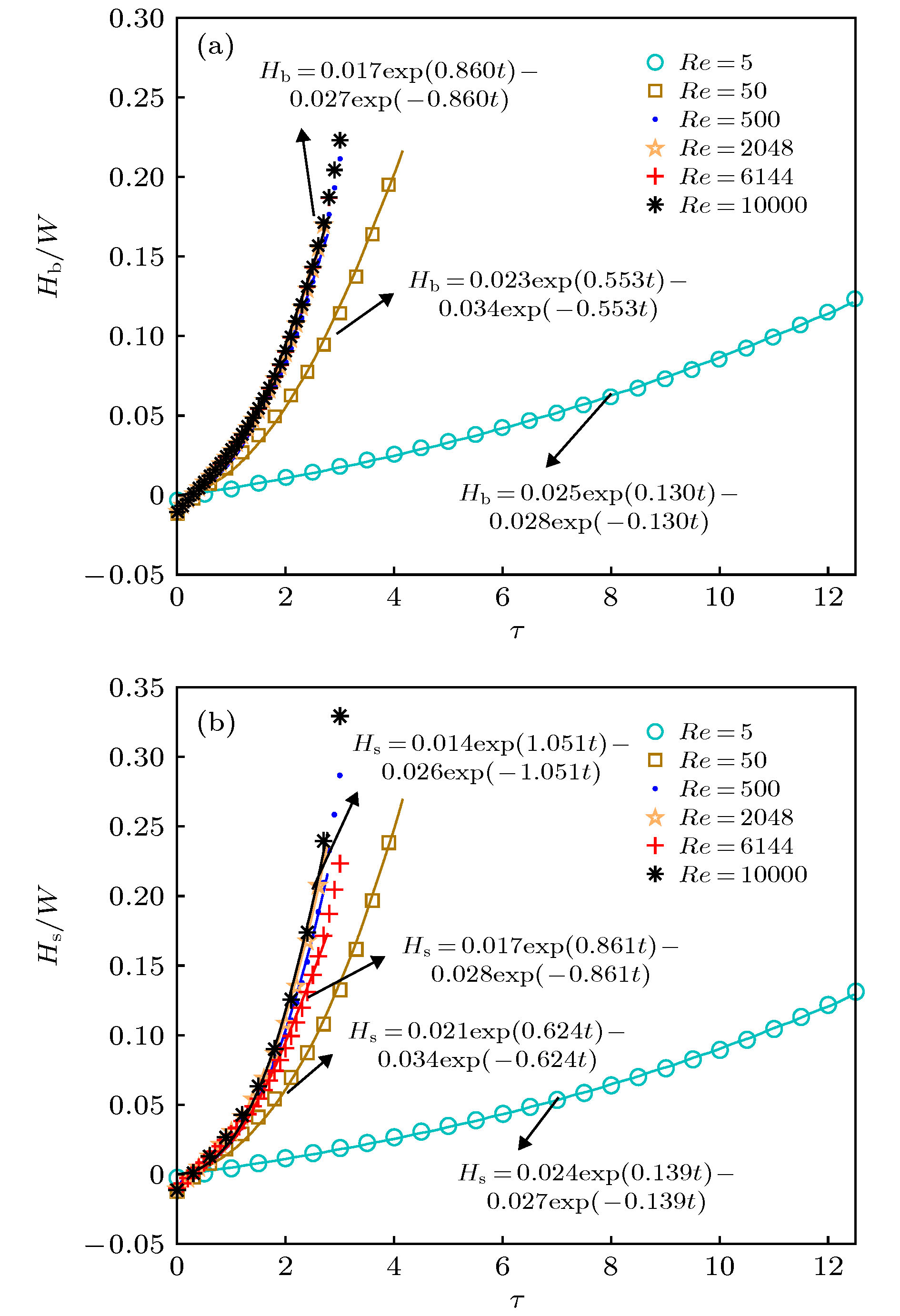
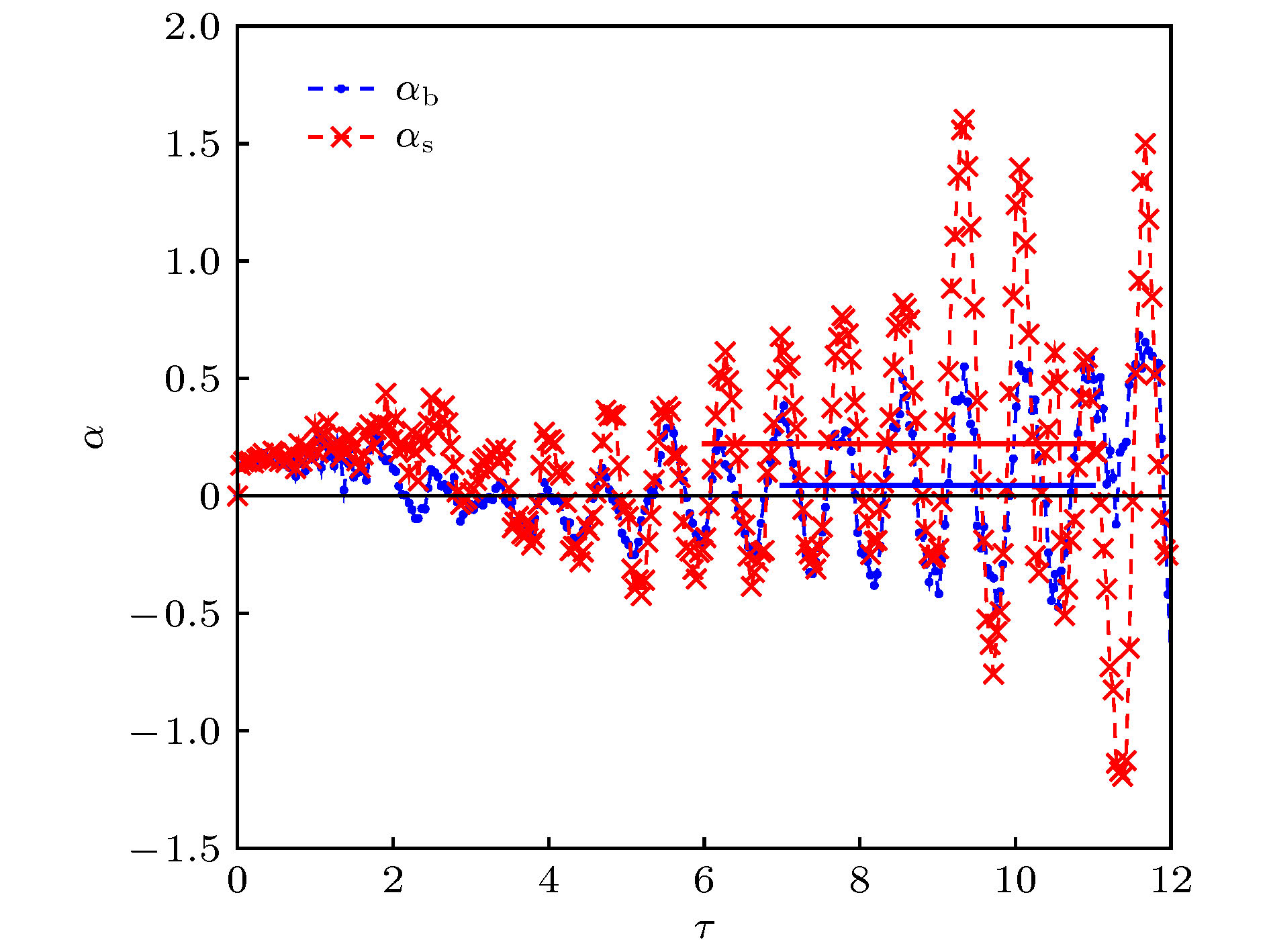
-
本文采用相场格子Boltzmann方法研究了竖直微通道内中等Atwoods数流体的单模Rayleigh-Taylor不稳定性问题, 系统分析了雷诺数对相界面动力学行为以及扰动在各发展阶段演化规律的影响. 数值结果表明高雷诺数条件下, 不稳定性界面扰动的增长经历了四个不同的发展阶段, 包括线性增长阶段、饱和速度阶段、重加速阶段及混沌混合阶段. 在线性增长阶段, 我们计算获得的气泡与尖钉振幅符合线性稳定性理论, 并且线性增长率随着雷诺数的增加而增大. 在第二个阶段, 我们观察到气泡与尖钉将以恒定的速度增长, 获得的尖钉饱和速度略高于Goncharov经典势能模型的解析解[Phys. Rev. Lett. 2002 88 134502], 这归因于系统中产生了多个尺度的旋涡, 而涡之间的相互作用促进了尖钉的增长. 随着横向速度和纵向速度的差异扩大, 气泡和尖钉界面演化诱导产生的Kelvin–Helmholtz不稳定性逐渐增强, 从而流体混合区域出现许多不同层次的涡结构, 加速了气泡与尖钉振幅的演化速度, 并在演化后期阶段, 导致界面发生多层次卷起、剧烈变形、混沌破裂等行为, 最终形成了非常复杂的拓扑结构. 此外, 我们还统计了演化后期气泡与尖钉的无量纲加速度, 发现气泡和尖钉的振幅在后期呈现二次增长规律, 其增长率系数分别为0.045与0.233. 而在低雷诺条件下, 重流体在不稳定性后期以尖钉的形式向下运动而轻流体以气泡的形式向上升起. 在整个演化过程中, 界面变得足够光滑, 气泡与尖钉在后期的演化速度接近于常数, 未观察到后期的重加速与混沌混合阶段.
-
关键词:
- 格子Boltzmann方法 /
- Rayleigh-Taylor不稳定性 /
- 相场方法 /
- 雷诺数 /
- 二次增长
In this paper, an advanced phase-field lattice Boltzmann method based on the multiple-relaxation-time collision model is used to simulate the immiscible single-mode Rayleigh-Taylor instability with a moderate Atwoods number in a long tube, and we systematically analyze the effect of the Reynolds number on the interfacial dynamics and the late-time development stages of interface disturbance. The highest Reynolds number in the current simulation reaches up to 10000. The numerical results show that the Reynolds number significantly affects the development of the instability. For high Reynolds numbers, the instability undergoes a sequence of different growth stages, which include the linear growth, saturated velocity growth, reacceleration, and chaotic mixing stages. In the linear growth stage, the developments of the bubble and spike conform to the classical linear growth theory, and it is shown that the growth rate increases with the Reynolds number. In the second stage, the bubble and spike evolve with the constant velocities, and the numerical prediction for spike velocity is found to be slightly larger than the solution of the potential flow theory proposed by Goncharov [Phys. Rev. Lett. 2002 88 134502], which can be attributed to the formation of vortices in the proximity of the spike tip. In addition, it is found that increasing the Reynolds number reduces the bubble saturated velocity, which then is smaller than the solution of the potential model. The nonlinear evolutions of the bubble and spike induce the Kelvin–Helmholtz instability, producing many vortex structures with different scales. Due to the interactions among the vortices, the instability eventually enters into the chaotic mixing stage, where the interfaces undergo the roll-up at multiple layers, sharp deformation, and chaotic breakup, forming a very complicated topology structure. Furthermore, we also measured the bubble and spike accelerations and find that the dimensionless values fluctuates around the constants of 0.045 and 0.233, indicating a mean quadratic growth. And for low Reynolds numbers, the heavy fluid will fall down in the form of the spike, and the interface in the whole process becomes very smooth without the appearances of the roll-up and vortices. The late-time evolutional stages such as the reacceleration and chaotic mixing cannot also be observed.-
Keywords:
- Lattice Boltzmann method /
- Rayleigh-Taylor instability /
- phase field /
- Reynolds number /
- quadratic growth
[1] Remington B A, Drake R P, Ryutov D D 2006 Rev. Mod. Phys. 78 755
Google Scholar
[2] Whitehead J A, Luther D S 1975 J. Geophys. Res. 80 705
Google Scholar
[3] Lindl J D, Amendt P, Berger R L, et al. 2004 Phys. Plasmas 11 339
Google Scholar
[4] Zhou C T, Yu M Y, He X T 2007 J. Appl. Phys. 101 103302
Google Scholar
[5] Rayleigh L 1883 Proc. London Math. Soc. 14 170
[6] Taylor G I 1950 Proc. R. Soc. London 201 192
Google Scholar
[7] Mitchner M, Landshoff R K M 1964 Phys. Fluids 7 862
Google Scholar
[8] Chandrasekhar S 1961 Hydrodynamic and Hydromagnetic Stability (Oxford: Oxford University Press) pp1−653
[9] Menikoff R, Mjolsness R C, Sharp D H, Zemach C 1977 Phys. Fluids 20 2000
Google Scholar
[10] Lewis D J 1950 Proc. R. Soc. London Ser. A 202 81
Google Scholar
[11] Sharp D H 1984 Physica D 12 3
Google Scholar
[12] Zhou Y 2017 Phys. Rep. 720−722 1
Google Scholar
[13] Zhou Y 2017 Phys. Rep. 723−725 1
Google Scholar
[14] Wei Y K, Wang Z D, Dou H S, Qian Y H 2017 Comput. Fluids 156 97
Google Scholar
[15] 李德梅, 赖惠林, 许爱国, 等 2018 67 080501
Google Scholar
Li D, Lai H, Xu A, et al. 2018 Acta Phys. Sin. 67 080501
Google Scholar
[16] Waddell J T, Niederhaus C E, Jacobs J W 2001 Phys. Fluids 13 1263
Google Scholar
[17] Goncharov V N 2002 Phys. Rev. Lett. 88 134502
Google Scholar
[18] Wilkinson J P, Jacobs J W 2007 Phys. Fluids 19 124102
Google Scholar
[19] He X Y, Zhang R Y, Chen S Y, Doolen G D 1999 Phys. Fluids 11 1143
Google Scholar
[20] Glimm J, Li X L, Lin A D 2002 Acta Math. Appl. Sin. 18 1
[21] Celani A, Mazzino A, Ginanneschi P M, Vozella L 2009 J. Fluid Mech. 622 115
Google Scholar
[22] Ramaprabhu P, Dimonte G, Woodward P, et al. 2012 Phys. Fluids 24 074107
Google Scholar
[23] Wei T, Livescu D 2012 Phys. Rev. E 86 046405
Google Scholar
[24] Liang H, Shi B C, Guo Z L, Chai Z H 2014 Phys. Rev. E 89 053320
Google Scholar
[25] Liang H, Li Q X, Shi B C, Chai Z H 2016 Phys. Rev. E 93 033113
Google Scholar
[26] Hu Z X, Zhang Y S, Tian B L, He Z W, Li L 2019 Phys. Fluids 31 104108
Google Scholar
[27] 郭照立, 郑楚光, 格子Boltzmann方法的原理及应用(北京: 科学出版社) 第1—250页
Guo Z L, Zheng C G 2009 Theory and Applications of Lattice Boltzmann Method (Beijing: Science Press) pp1−250 (in Chinese)
[28] Liang H, Chai Z H, Shi B C, Guo Z L, Zhang T 2014 Phys. Rev. E 90 063311
Google Scholar
[29] Liang H, Li Y, Chen J X, Xu J R 2019 Int. J. Heat Mass Tranfer 130 1189
Google Scholar
[30] Liang H, Shi B C, Chai Z H 2016 Phys. Rev. E 93 013308
Google Scholar
[31] Liang H, Xu J R, Chen J X, Chai Z H, Shi B C 2019 Appl. Math. Model. 73 487
Google Scholar
[32] 娄钦, 李涛, 杨茉 2018 67 234701
Google Scholar
Lou Q, Li T, Yang M 2018 Acta Phys. Sin. 67 234701
Google Scholar
[33] 臧晨强, 娄钦 2017 66 134701
Google Scholar
Zang C Q, Lou Q 2017 Acta Phys. Sin. 66 134701
Google Scholar
[34] 梁宏, 柴振华, 施保昌 2016 65 204701
Google Scholar
Liang H, Chai Z H, Shi B C 2016 Acta Phys. Sin. 65 204701
Google Scholar
[35] Liang H, Liu H H, Chai Z H, Shi B C 2019 Phys. Rev. E 99 063306
Google Scholar
[36] Lallemand P, Luo LS 2000 Phys. Rev. E 61 6546
[37] Wei Y K, Wang Z D, Yang J F, Dou H S, Qian Y H 2015 Comput. Fluids 118 167
Google Scholar
[38] Wei Y K, Yang H, Lin Z, Wang Z D, Qian Y H 2018 Appl. Math. Comput. 339 556
[39] Liang H, Xu J R, Chen J X, Wang H L, Chai Z H, Shi B C 2018 Phys. Rev. E 97 033309
Google Scholar
[40] Abarzhi S I, Gorobets A, Sreenivasan K R 2005 Phys. Fluids 17 081705
Google Scholar
[41] Sreenivasan K R 1984 Phys. Fluids 27 1048
Google Scholar
-
图 1 雷诺数对非混相RT不稳定性中相界面演化图案的影响 (a)
$ Re = 10000 $ ; (b)$ Re = 2048 $ ; (c)$ Re = 50 $ ; (d)$ Re = 5 $ Fig. 1. The effect of the Reynolds number on the evolution of interfacial patterns in the immiscible RT instability: (a)
$ Re = 10000 $ ; (b)$ Re = 2048 $ ; (c)$ Re = 50 $ ; (d)$ Re = 5 $ .
图 2 雷诺数对无量纲化的气泡与尖钉随时间演化振幅的影响
Fig. 2. The effect of the Reynolds number on the dimensionless bubble and spike amplitudes.
图 3 雷诺数对无量纲化的气泡和尖钉演化速度的影响
Fig. 3. The effect of the Reynolds number on the dimensionless bubble and spike velocities.
图 4 不同雷诺数下, 气泡和尖钉振幅在初始阶段的演化曲线, 其中数据点是统计结果, 实线则是拟合结果
Fig. 4. The curves of the early-time bubble and spike amplitudes with different Reynolds numbers, where the data points and solid lines are the statistical and fitting results.
图 5 高雷诺数下, 气泡和尖钉的无量纲加速度演化曲线, 红色和蓝色实线分别为0.045和0.233
Fig. 5. The curves of dimensionless bubble and spike accelerations at a high Reynolds number, and the red and blue solid lines are 0.045 and 0.233.
-
[1] Remington B A, Drake R P, Ryutov D D 2006 Rev. Mod. Phys. 78 755
Google Scholar
[2] Whitehead J A, Luther D S 1975 J. Geophys. Res. 80 705
Google Scholar
[3] Lindl J D, Amendt P, Berger R L, et al. 2004 Phys. Plasmas 11 339
Google Scholar
[4] Zhou C T, Yu M Y, He X T 2007 J. Appl. Phys. 101 103302
Google Scholar
[5] Rayleigh L 1883 Proc. London Math. Soc. 14 170
[6] Taylor G I 1950 Proc. R. Soc. London 201 192
Google Scholar
[7] Mitchner M, Landshoff R K M 1964 Phys. Fluids 7 862
Google Scholar
[8] Chandrasekhar S 1961 Hydrodynamic and Hydromagnetic Stability (Oxford: Oxford University Press) pp1−653
[9] Menikoff R, Mjolsness R C, Sharp D H, Zemach C 1977 Phys. Fluids 20 2000
Google Scholar
[10] Lewis D J 1950 Proc. R. Soc. London Ser. A 202 81
Google Scholar
[11] Sharp D H 1984 Physica D 12 3
Google Scholar
[12] Zhou Y 2017 Phys. Rep. 720−722 1
Google Scholar
[13] Zhou Y 2017 Phys. Rep. 723−725 1
Google Scholar
[14] Wei Y K, Wang Z D, Dou H S, Qian Y H 2017 Comput. Fluids 156 97
Google Scholar
[15] 李德梅, 赖惠林, 许爱国, 等 2018 67 080501
Google Scholar
Li D, Lai H, Xu A, et al. 2018 Acta Phys. Sin. 67 080501
Google Scholar
[16] Waddell J T, Niederhaus C E, Jacobs J W 2001 Phys. Fluids 13 1263
Google Scholar
[17] Goncharov V N 2002 Phys. Rev. Lett. 88 134502
Google Scholar
[18] Wilkinson J P, Jacobs J W 2007 Phys. Fluids 19 124102
Google Scholar
[19] He X Y, Zhang R Y, Chen S Y, Doolen G D 1999 Phys. Fluids 11 1143
Google Scholar
[20] Glimm J, Li X L, Lin A D 2002 Acta Math. Appl. Sin. 18 1
[21] Celani A, Mazzino A, Ginanneschi P M, Vozella L 2009 J. Fluid Mech. 622 115
Google Scholar
[22] Ramaprabhu P, Dimonte G, Woodward P, et al. 2012 Phys. Fluids 24 074107
Google Scholar
[23] Wei T, Livescu D 2012 Phys. Rev. E 86 046405
Google Scholar
[24] Liang H, Shi B C, Guo Z L, Chai Z H 2014 Phys. Rev. E 89 053320
Google Scholar
[25] Liang H, Li Q X, Shi B C, Chai Z H 2016 Phys. Rev. E 93 033113
Google Scholar
[26] Hu Z X, Zhang Y S, Tian B L, He Z W, Li L 2019 Phys. Fluids 31 104108
Google Scholar
[27] 郭照立, 郑楚光, 格子Boltzmann方法的原理及应用(北京: 科学出版社) 第1—250页
Guo Z L, Zheng C G 2009 Theory and Applications of Lattice Boltzmann Method (Beijing: Science Press) pp1−250 (in Chinese)
[28] Liang H, Chai Z H, Shi B C, Guo Z L, Zhang T 2014 Phys. Rev. E 90 063311
Google Scholar
[29] Liang H, Li Y, Chen J X, Xu J R 2019 Int. J. Heat Mass Tranfer 130 1189
Google Scholar
[30] Liang H, Shi B C, Chai Z H 2016 Phys. Rev. E 93 013308
Google Scholar
[31] Liang H, Xu J R, Chen J X, Chai Z H, Shi B C 2019 Appl. Math. Model. 73 487
Google Scholar
[32] 娄钦, 李涛, 杨茉 2018 67 234701
Google Scholar
Lou Q, Li T, Yang M 2018 Acta Phys. Sin. 67 234701
Google Scholar
[33] 臧晨强, 娄钦 2017 66 134701
Google Scholar
Zang C Q, Lou Q 2017 Acta Phys. Sin. 66 134701
Google Scholar
[34] 梁宏, 柴振华, 施保昌 2016 65 204701
Google Scholar
Liang H, Chai Z H, Shi B C 2016 Acta Phys. Sin. 65 204701
Google Scholar
[35] Liang H, Liu H H, Chai Z H, Shi B C 2019 Phys. Rev. E 99 063306
Google Scholar
[36] Lallemand P, Luo LS 2000 Phys. Rev. E 61 6546
[37] Wei Y K, Wang Z D, Yang J F, Dou H S, Qian Y H 2015 Comput. Fluids 118 167
Google Scholar
[38] Wei Y K, Yang H, Lin Z, Wang Z D, Qian Y H 2018 Appl. Math. Comput. 339 556
[39] Liang H, Xu J R, Chen J X, Wang H L, Chai Z H, Shi B C 2018 Phys. Rev. E 97 033309
Google Scholar
[40] Abarzhi S I, Gorobets A, Sreenivasan K R 2005 Phys. Fluids 17 081705
Google Scholar
[41] Sreenivasan K R 1984 Phys. Fluids 27 1048
Google Scholar
下载:
计量
- 文章访问数: 7884
- PDF下载量: 124
- 被引次数: 0
