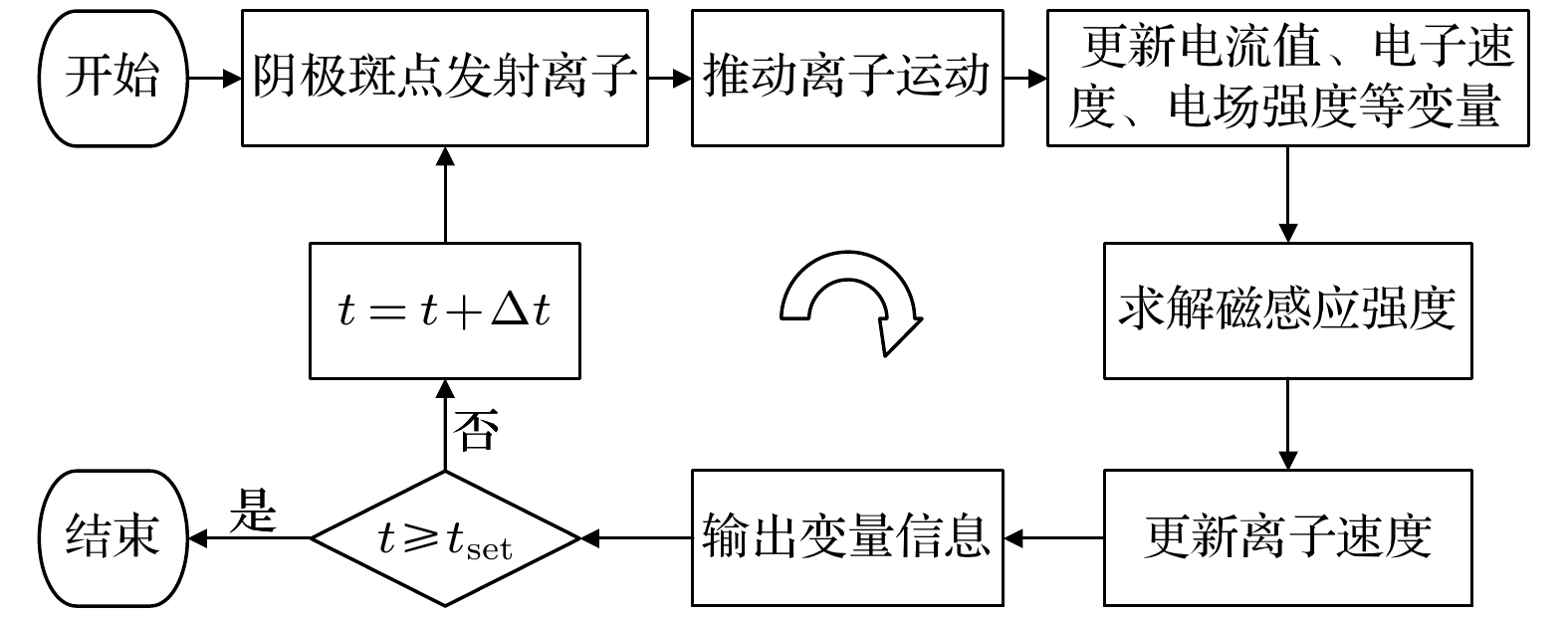
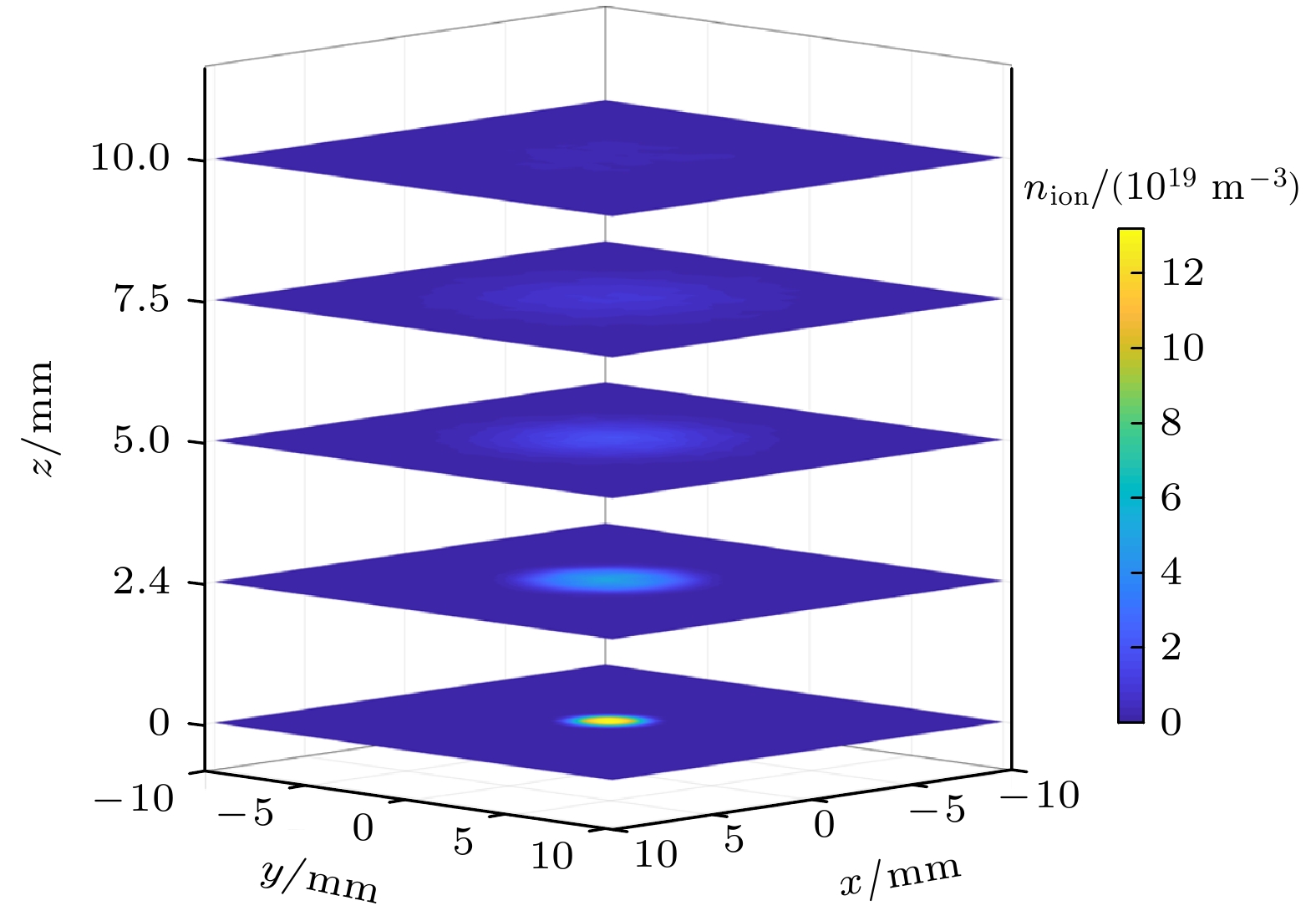
-
Vacuum arc is a special metal vapor discharge phenomenon, because its discharge medium totally comes from the evaporation and ionization of electrode materials. In the case of low current, the vacuum arc is completely composed of plasma jets emitted from discrete cathode spots on the cathode surface and the current carried by each spot depends on the cathode material. When the arc current exceeds a certain value, a certain number of cathode spot plasma jets will appear. Vacuum arcs play a very important role in some industrial applications such as vacuum circuit breakers, vacuum coatings and electric thrusters. As an important plasma control method, the external axial magnetic field (AMF) has an important influence on the macroscopic morphology and microscopic parameter distribution of the vacuum arc. Various studies of vacuum arc under AMF have been carried out and some progress has been made. However, the existing literature about the simulation research of vacuum arc is mostly concentrated in the case of large current, and less attention is paid to the case of small current. The reason is that the traditional methods, magneto-hydrodynamics or particle-in-cell, are limited by either accuracy or efficiency, and cannot be effectively applied to the low current vacuum arc plasma jet simulations. In this paper, we develop a fully three-dimensional hybrid plasma simulation algorithm to study the single cathode spot vacuum arc plasma jet under AMF. In this model, ions are modelled as particles while electrons are treated as massless fluid, and the self-generated magnetic field is also considered. To simplify the condition, the cathode spot in our model only exists as a plasma jet source, thus the detailed mechanism of producing plasmas is neglected. And the movement of the cathode spot is not considered either. The results show that the single cathode spot plasma jet diffuses into the interelectrode in a cone shape after leaving the cathode spot, and the ion density drops rapidly from cathode to anode. Under the simulation conditions in this paper (I ≤ 150 A), the self-generated magnetic field will not have a significant influence on the plasma jet itself in the case of low current. The external AMF has a compressive effect on the diffusion of the vacuum arc plasma jet. Under the AMF, the radial movement of the ions is suppressed, and the decrease of the ion radial velocity leads to a smaller diffusion radius of the jet. This compression effect of the AMF on the plasma jet is related to both the intensity of the external AMF and the magnitude of the arc current. In the case of a constant arc current magnitude, the compression effect gradually increases as the value of the AMF intensity gradually increases; in the case of a constant value of the external AMF, the compression effect gradually decreases as the current gradually becomes larger.
-
Keywords:
- vacuum arc /
- plasma jet /
- hybrid model /
- axial magnetic field
[1] Beilis I I 2001 IEEE Trans. Plasma Sci. 29 657
Google Scholar
[2] 王建华, 耿英三, 刘志远, 闫静 2017 高压电器 53 1
Google Scholar
Wang J H, Geng Y S, Liu Z Y, Yan J 2017 High Volt. Appar. 53 1
Google Scholar
[3] Sanders D M, Anders A 2000 Surf. Coat. Technol. 133 78
Google Scholar
[4] Geng J Y, Chen Y C, Sun S R, Huang W D, Wang H X 2020 Plasma Sci. Technol. 22 094012
Google Scholar
[5] Keidar M, Zhuang T, Shashurin A, Teel G, Chiu D, Lukas J, Haque S, Brieda L 2014 Plasma Phys. Controlled Fusion 57 014005
Google Scholar
[6] 王立军, 贾申利, 杨泽, 史宗谦 2017 高压电器 3 22
Google Scholar
Wang L J, Jia S L, Yang Z, Shi Z Q 2017 High Volt. Appar. 3 22
Google Scholar
[7] Rondeel W G J 1975 J. Phys. D: Appl. Phys. 8 934
Google Scholar
[8] Keidar M, Schulman M B 2001 IEEE Trans. Plasma Sci. 29 684
Google Scholar
[9] 王立军, 贾申利, 史宗谦, 荣命哲 2005 中国电机工程学报 25 113
Google Scholar
Wang L J, Jia S L, Shi Z Q, Rong M Z 2005 Chin. Soc. for Elec. Eng. 25 113
Google Scholar
[10] Jia S L, Zhang L, Wang L J, Chen B, Shi Z Q, Sun W 2011 IEEE Trans. Plasma Sci. 39 3233
Google Scholar
[11] Wang C, Shi Z Q, Wu B Z, Gao Z P, Jia S L, Wang L J 2016 J. Phys. D: Appl. Phys. 49 135203
Google Scholar
[12] 李晗蔚, 孙安邦, 张幸, 姚聪伟, 常正实, 张冠军 2018 4 143
Google Scholar
Li H W, Sun A B, Zhang X, Yao C W, Chang Z S, Zhang G J 2018 Acta Phys. Sin. 4 143
Google Scholar
[13] Shmelev D L, Uimanov I V 2015 IEEE Trans. Plasma Sci. 43 2261
Google Scholar
[14] Shmelev D L, Oreshkin V I, Uimanov I V 2019 IEEE Trans. Plasma Sci. 47 3478
Google Scholar
[15] Li C, Ebert U, Hundsdorfer W 2010 J. Comput. Phys. 229 200
Google Scholar
[16] Arai K, Takahashi S, Morimiya O, Niwa Y 2003 IEEE Trans. Plasma Sci. 31 929
Google Scholar
[17] Kutzner J, Miller H C 1992 J. Phys. D: Appl. Phys. 25 686
Google Scholar
[18] Winske D, Omidi N 1991 Hybrid Codes: Methods and Applications (New Mexico: Los Alamos National Lab.) pp103−160
[19] Beilis I I, Keidar M, Boxman R L, Goldsmith S 1998 J. Appl. Phys. 83 709
Google Scholar
[20] Tóth G 2000 J. Comput. Phys. 161 605
Google Scholar
[21] Harned D S 1982 J. Comput. Phys. 47 452
Google Scholar
[22] Schade E, Shmelev D L 2003 IEEE Trans. Plasma Sci. 31 890
Google Scholar
[23] Kutzner J, Miller H C 1989 IEEE Trans. Plasma Sci. 17 688
Google Scholar
-
图 1 物理模型示意图
Figure 1. The schematic of physical model.
图 2 程序执行步骤
Figure 2. Execution steps of the program.
图 3 三维空间离子数密度分布
Figure 3. The distribution of ion number density in 3D space.
图 4 (a) 轴向电流密度分布; (b)自生磁感应强度分布 I = 30 A, Bz = 0 mT
Figure 4. (a) The distribution of axial current density; (b) the distribution of self-generated azimuthal magnetic field I = 30 A, Bz = 0 mT
图 5 在I= 30 A时不同外施纵磁条件下离子数密度分布 (a) Bz = 0 mT; (b) Bz = 25 mT; (c) Bz = 50 mT; (d) Bz = 75 mT
Figure 5. Ion number density distributions under different external AMFs at I= 30 A: (a) Bz = 0 mT; (b) Bz = 25 mT; (c) Bz = 50 mT; (d) Bz = 75 mT.
图 6 不同外施纵磁条件下轴线上离子数密度变化
Figure 6. Ion number density distributions along the axis under different external AMFs.
图 7 不同外施磁场条件下离子沿x方向速度在x-z平面的相空间分布
Figure 7. Phase diagram of ion velocity along x-direction in x-z plane under different external AMFs.
图 8 在Bz = 75 mT时不同电弧电流条件下离子数密度分布 (a) I = 30 A; (b) I = 60 A; (c) I = 90 A; (d) I = 120 A
Figure 8. Ion number density distributions with different arc currents at Bz = 75 mT: (a) I = 30 A; (b) I = 60 A; (c) I = 90 A; (d) I = 120 A.
图 9 轴线上阳极处离子数密度与阴极处离子数密度的比值
Figure 9. The ratios of the ion number density at the anode to that at the cathode on the axis.
-
[1] Beilis I I 2001 IEEE Trans. Plasma Sci. 29 657
Google Scholar
[2] 王建华, 耿英三, 刘志远, 闫静 2017 高压电器 53 1
Google Scholar
Wang J H, Geng Y S, Liu Z Y, Yan J 2017 High Volt. Appar. 53 1
Google Scholar
[3] Sanders D M, Anders A 2000 Surf. Coat. Technol. 133 78
Google Scholar
[4] Geng J Y, Chen Y C, Sun S R, Huang W D, Wang H X 2020 Plasma Sci. Technol. 22 094012
Google Scholar
[5] Keidar M, Zhuang T, Shashurin A, Teel G, Chiu D, Lukas J, Haque S, Brieda L 2014 Plasma Phys. Controlled Fusion 57 014005
Google Scholar
[6] 王立军, 贾申利, 杨泽, 史宗谦 2017 高压电器 3 22
Google Scholar
Wang L J, Jia S L, Yang Z, Shi Z Q 2017 High Volt. Appar. 3 22
Google Scholar
[7] Rondeel W G J 1975 J. Phys. D: Appl. Phys. 8 934
Google Scholar
[8] Keidar M, Schulman M B 2001 IEEE Trans. Plasma Sci. 29 684
Google Scholar
[9] 王立军, 贾申利, 史宗谦, 荣命哲 2005 中国电机工程学报 25 113
Google Scholar
Wang L J, Jia S L, Shi Z Q, Rong M Z 2005 Chin. Soc. for Elec. Eng. 25 113
Google Scholar
[10] Jia S L, Zhang L, Wang L J, Chen B, Shi Z Q, Sun W 2011 IEEE Trans. Plasma Sci. 39 3233
Google Scholar
[11] Wang C, Shi Z Q, Wu B Z, Gao Z P, Jia S L, Wang L J 2016 J. Phys. D: Appl. Phys. 49 135203
Google Scholar
[12] 李晗蔚, 孙安邦, 张幸, 姚聪伟, 常正实, 张冠军 2018 4 143
Google Scholar
Li H W, Sun A B, Zhang X, Yao C W, Chang Z S, Zhang G J 2018 Acta Phys. Sin. 4 143
Google Scholar
[13] Shmelev D L, Uimanov I V 2015 IEEE Trans. Plasma Sci. 43 2261
Google Scholar
[14] Shmelev D L, Oreshkin V I, Uimanov I V 2019 IEEE Trans. Plasma Sci. 47 3478
Google Scholar
[15] Li C, Ebert U, Hundsdorfer W 2010 J. Comput. Phys. 229 200
Google Scholar
[16] Arai K, Takahashi S, Morimiya O, Niwa Y 2003 IEEE Trans. Plasma Sci. 31 929
Google Scholar
[17] Kutzner J, Miller H C 1992 J. Phys. D: Appl. Phys. 25 686
Google Scholar
[18] Winske D, Omidi N 1991 Hybrid Codes: Methods and Applications (New Mexico: Los Alamos National Lab.) pp103−160
[19] Beilis I I, Keidar M, Boxman R L, Goldsmith S 1998 J. Appl. Phys. 83 709
Google Scholar
[20] Tóth G 2000 J. Comput. Phys. 161 605
Google Scholar
[21] Harned D S 1982 J. Comput. Phys. 47 452
Google Scholar
[22] Schade E, Shmelev D L 2003 IEEE Trans. Plasma Sci. 31 890
Google Scholar
[23] Kutzner J, Miller H C 1989 IEEE Trans. Plasma Sci. 17 688
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 5690
- PDF Downloads: 134
- Cited By: 0
