激波与轻质气柱作用过程的磁场抑制特性

张升博; 张焕好; 张军; 毛勇建; 陈志华; 石启陈; 郑纯

doi:10.7498/aps.73.20231916

摘要

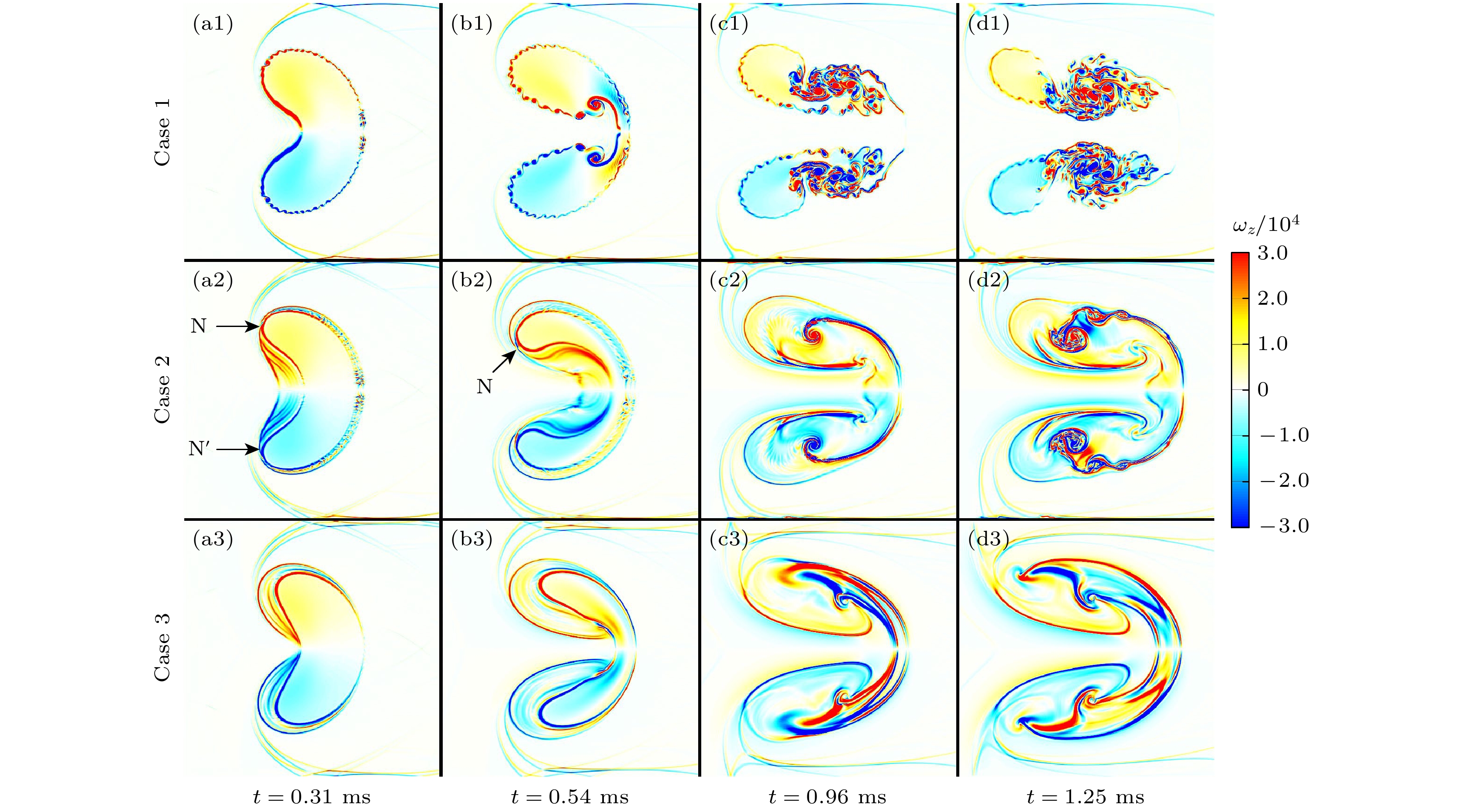
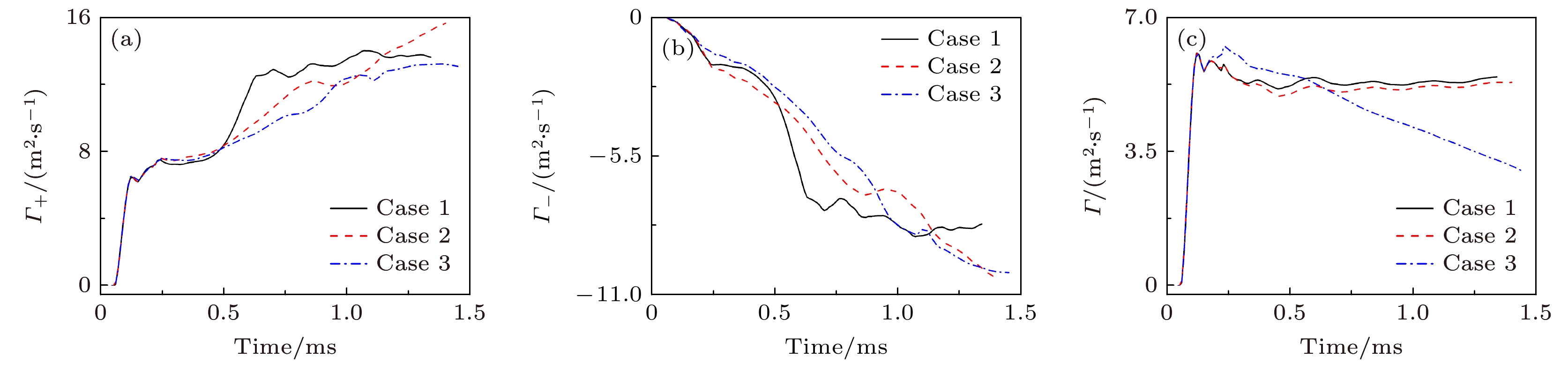
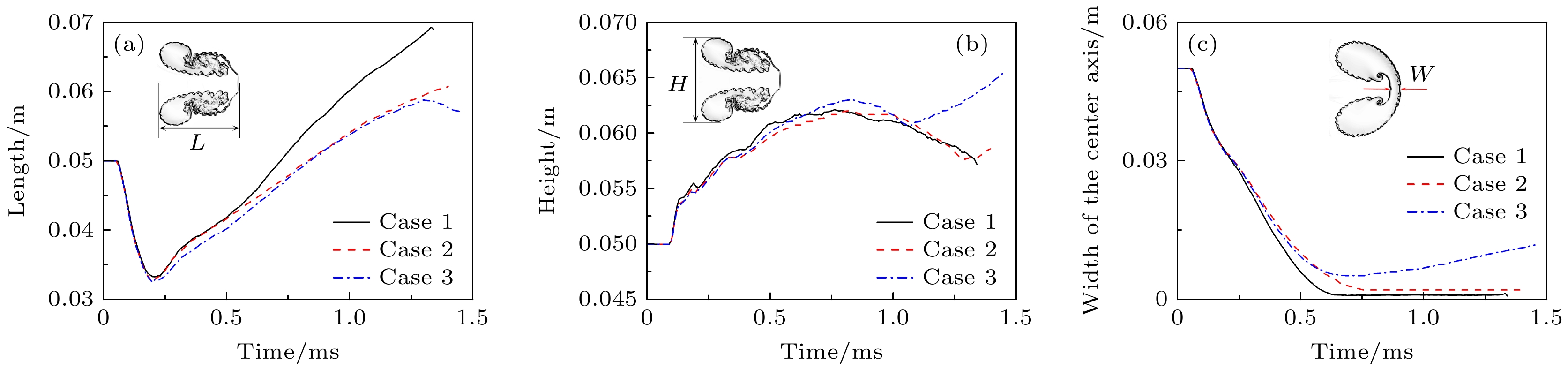
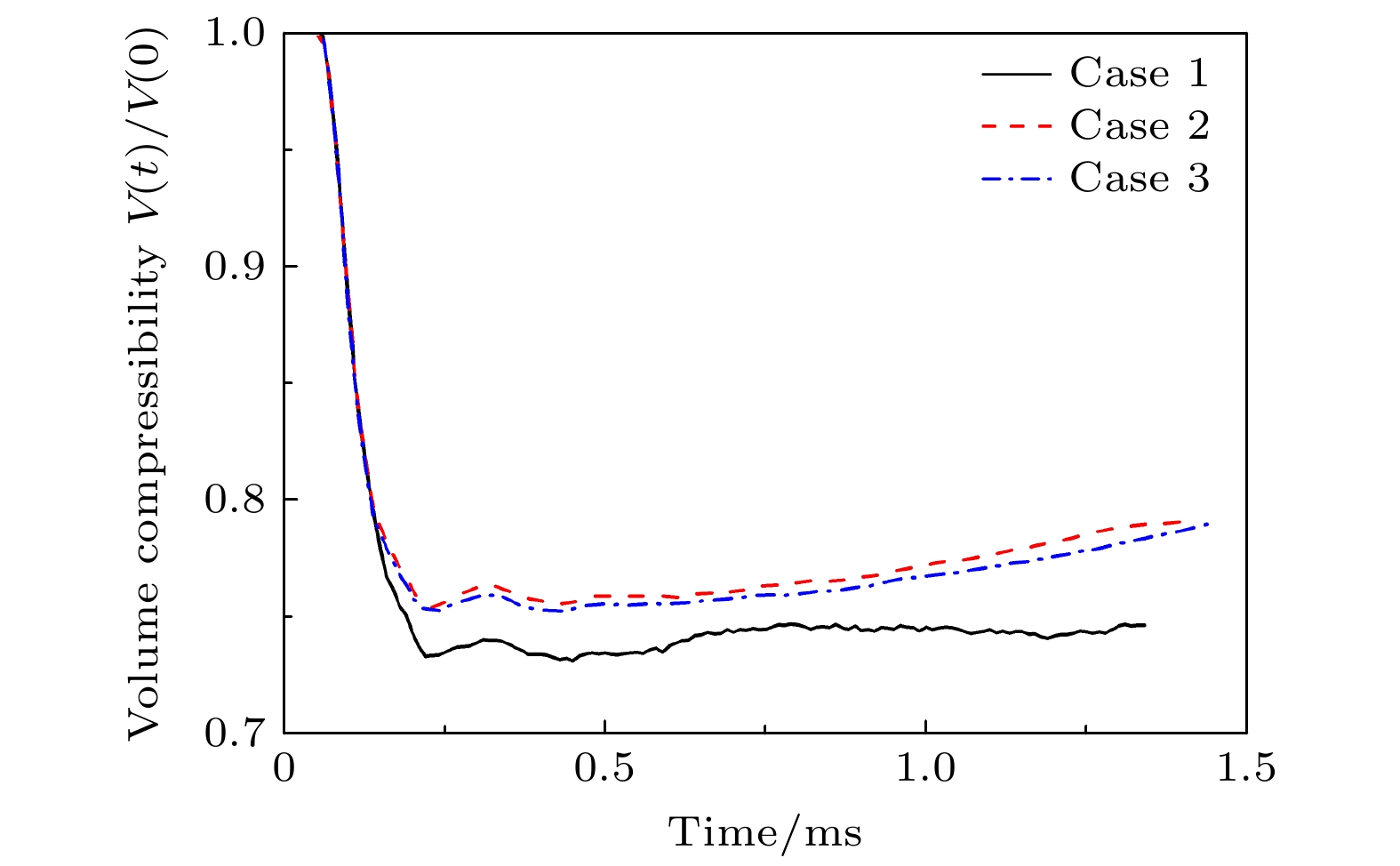
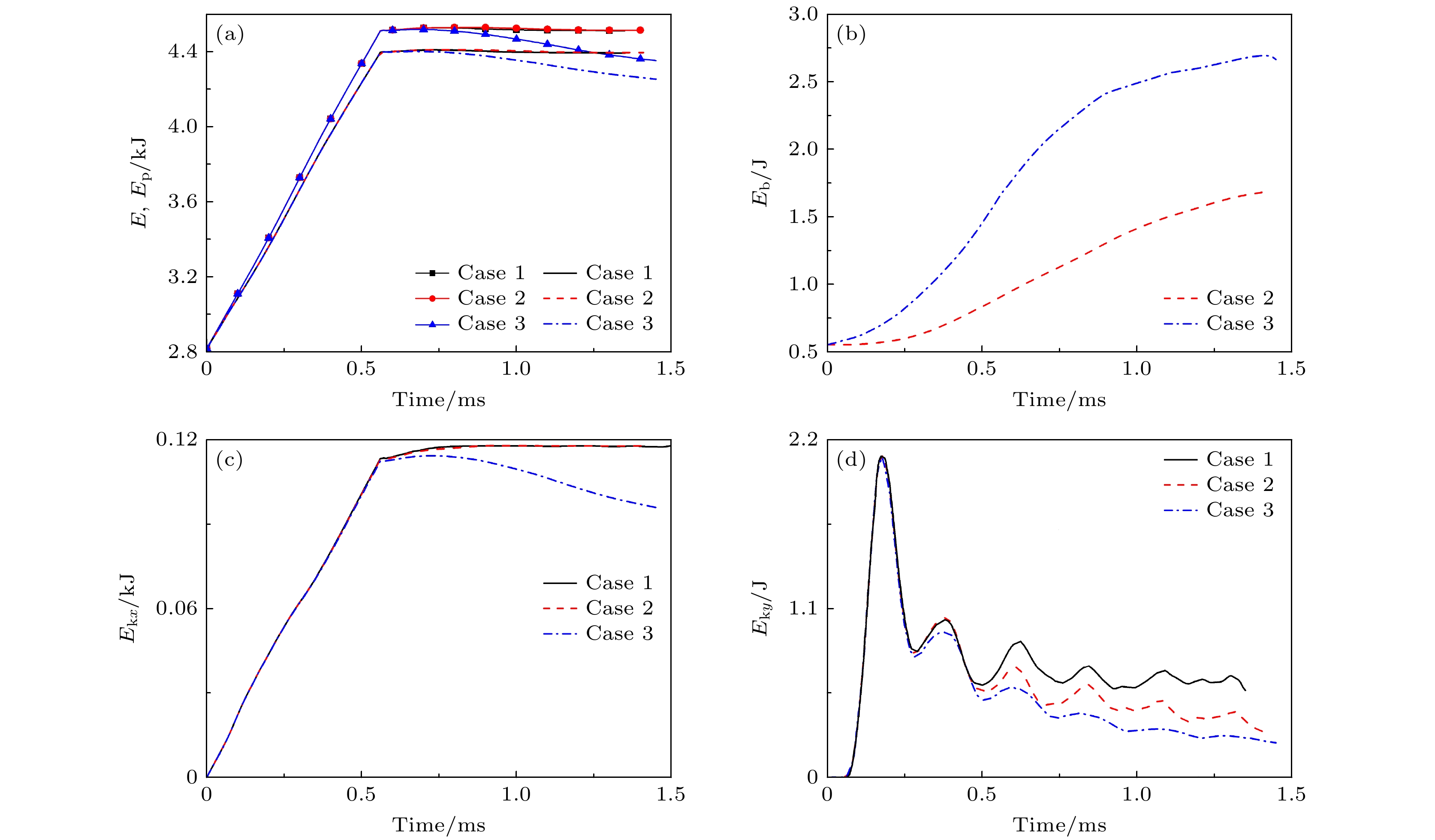
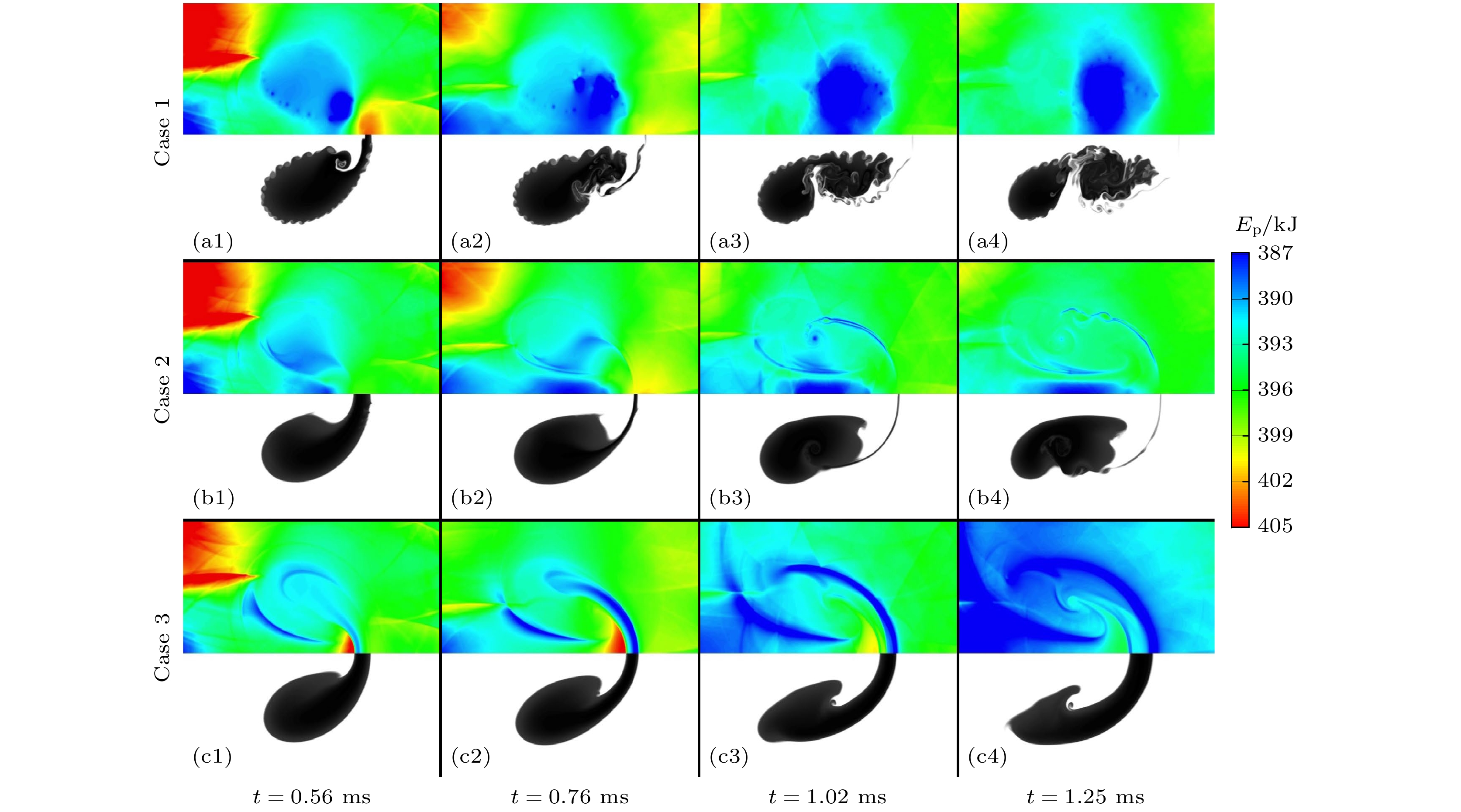
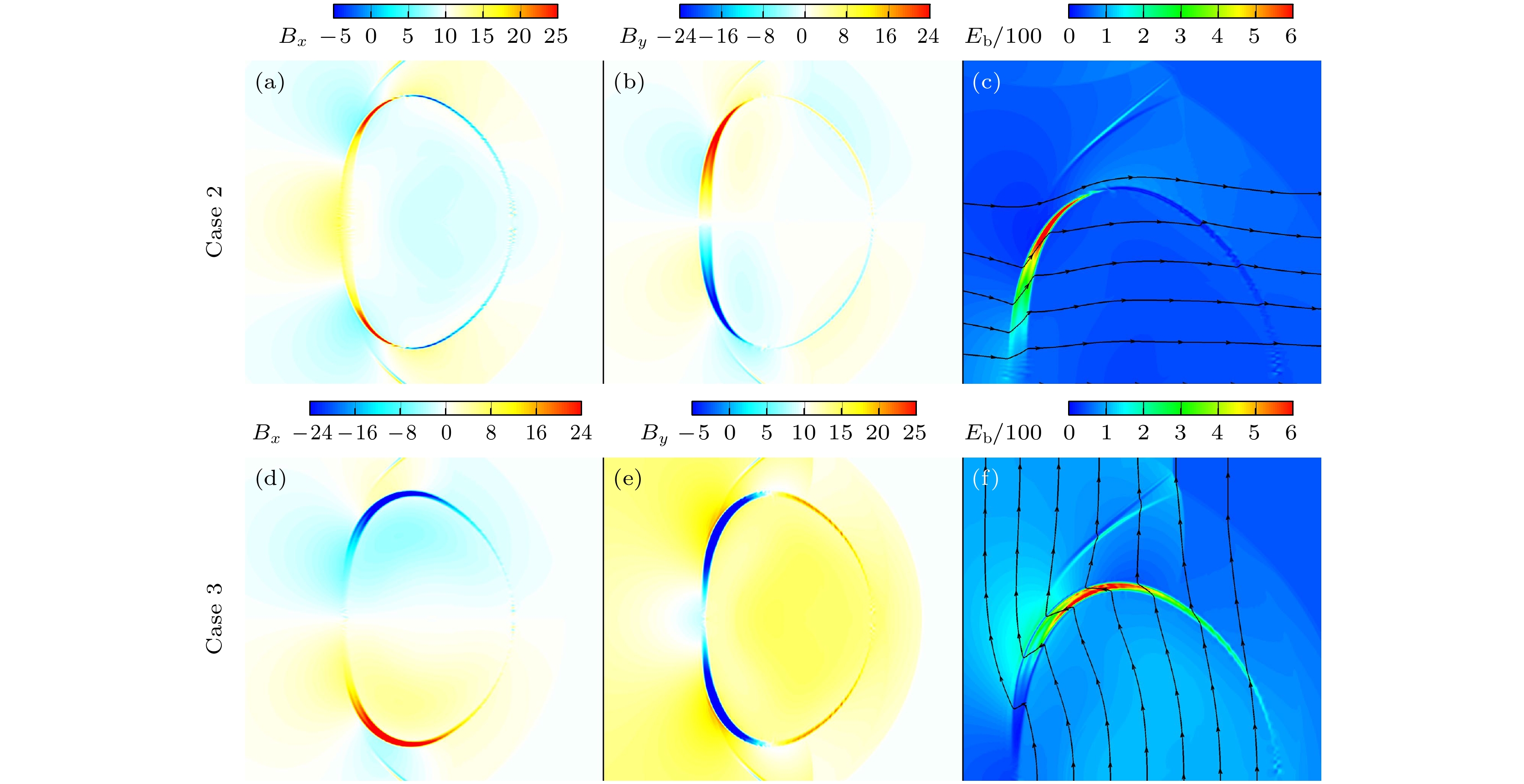
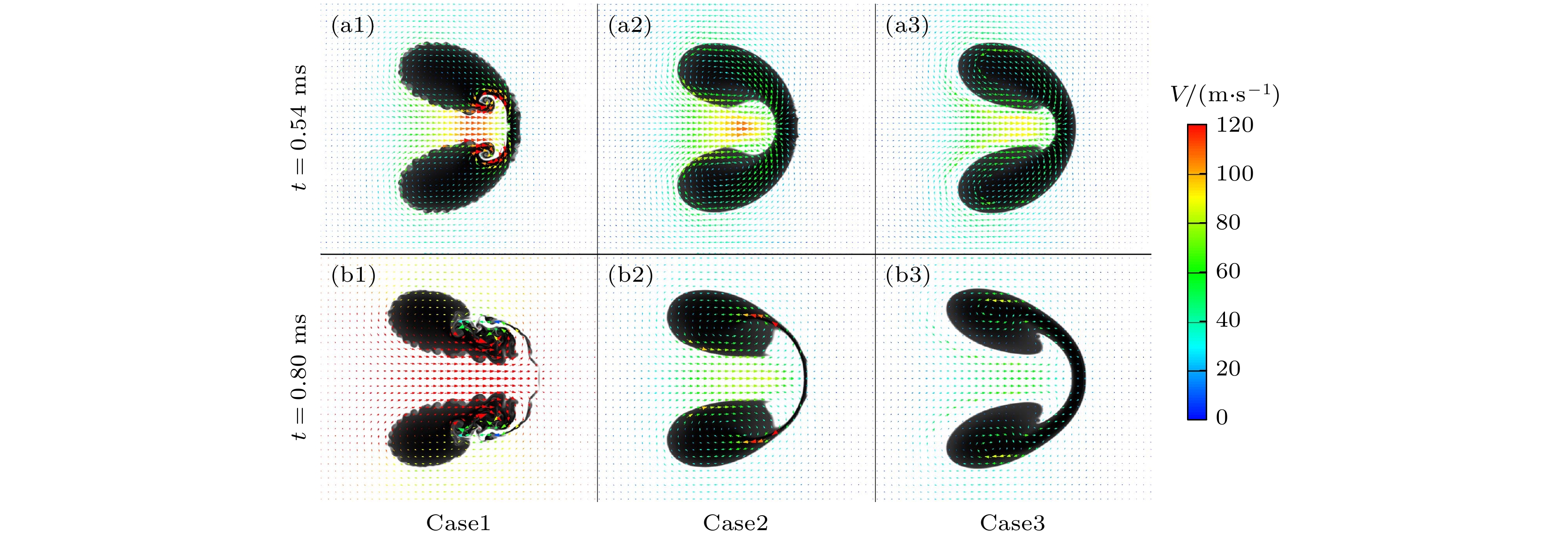
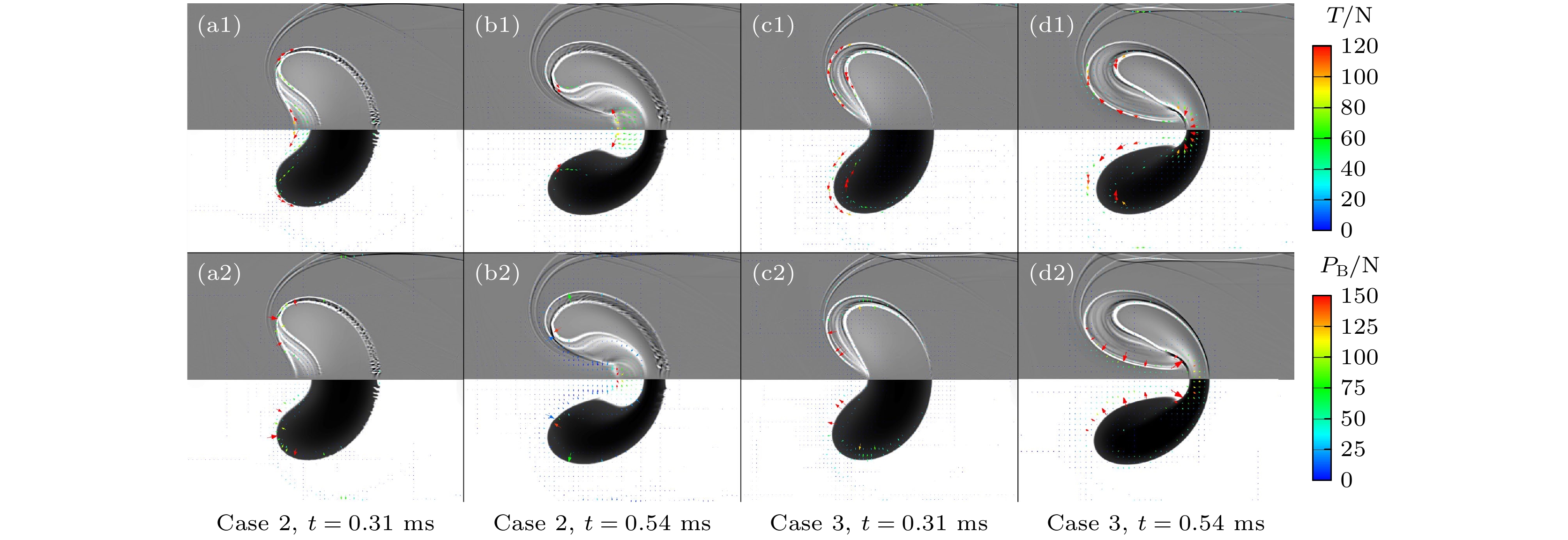
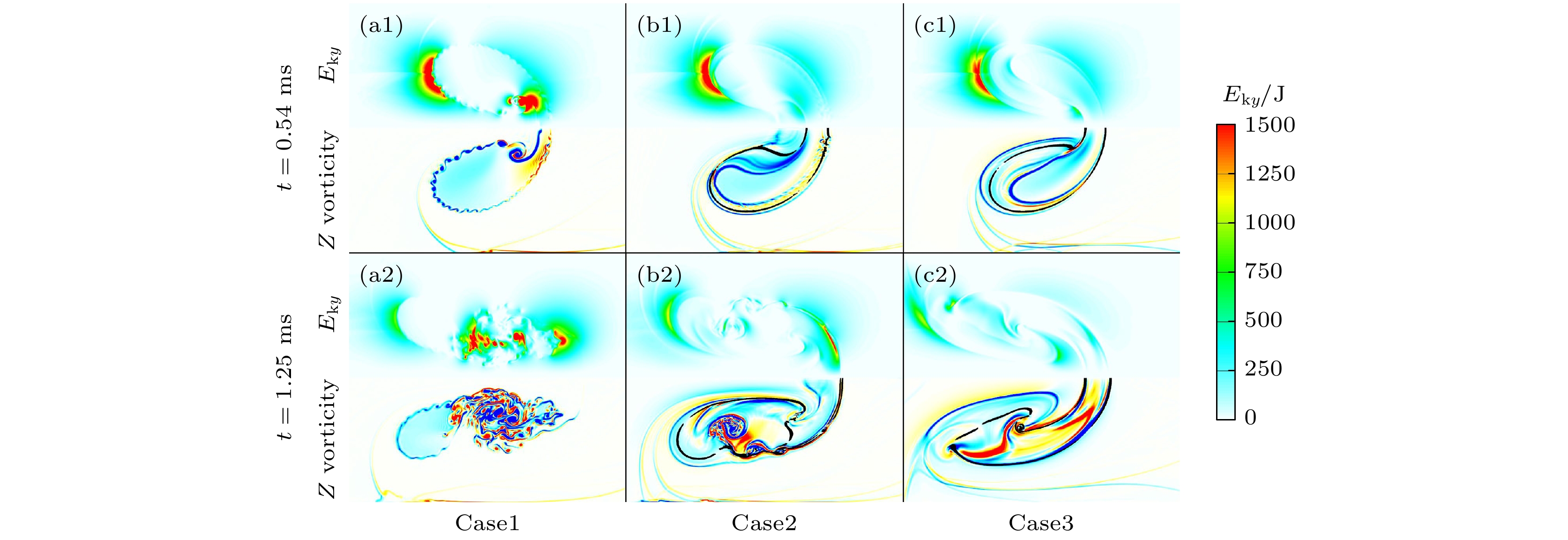
本文采用CTU (corner transport upwind)+CT (constrained transport)算法求解理想可压缩磁流体动力学(magneto-hydro-dynamic, MHD)方程, 仿真研究了不同方向磁场控制下高斯分布轻质气柱界面受平面冲击波扰动后的演化过程, 揭示了磁场方向对界面不稳定性的影响机理. 仿真结果探讨了有/无磁场作用下流场特性与波系结构的发展, 对比分析了磁场方向对气柱的长度、高度、射流宽度和体积压缩率的影响, 并结合流场上半区环量、能量分量、速度和磁场力分布, 多角度分析了磁场方向对界面不稳定性的影响机理. 结果表明, 磁压力推动涡量远离界面, 降低了涡量在密度界面上的沉积而附着在分裂后的涡层上, 从而有效抑制Richtmyer-Meshkov不稳定性对界面的影响; 由于磁张力附着在被分离的涡层上, 且其作用方向与界面因速度剪切而卷起涡的方向相反, 因此抑制了界面因Kelvin-Helmholtz不稳定性而形成涡串. 另外, 纵向磁场控制下的磁张力反作用于中轴射流方向, 同样抑制了Rayleigh-Taylor 不稳定性的发展.

关键词:

Abstract

Based on ideal compressible magnetohydrodynamics (MHD) equations, the interface instabilities induced by the interaction between planar shock wave and the light gas (Helium) cylinder under the influence of the magnetic fields with different directions are investigated numerically by using the CTU(corner transport upwind)+CT (constrained transport) algorithm. The numerical results elucidate the evolution of flow field characteristics and wave structures with and without magnetic field. Moreover, we examine the influence of the magnetic field direction on a characteristic scales (including the length, height and width of the central axis of gas cylinder), as well as the volume compressibility. Then, the mechanism of the magnetic field direction affecting the interface instability is studied in depth by integrating the analyses of the circulation, energy, velocity and magnetic force distribution within the flow field. The core of this study, is to explore the suppression mechanism of interface instability by magnetic field force. The results show that the magnetic pressure plays a crucial role in driving vorticity away from the interface, thereby reducing its deposition on the density interface. Simultaneously, it adheres to the divided vortex layer, thereby effectively isolating the influence of Richtmyer-Meshkov instability on the interface. On the other hand, the magnetic tension adheres to the separated vortex layer, and its direction is opposite to that of the vorticity generated by the shear of interface velocity. This action effectively suppresses the Kelvin-Helmholtz instability and the rolling-up of vortices on the density interface. Additionally, under the control of a longitudinal magnetic field, the direction of magnetic tension is opposite to the direction of the central jet, effectively suppressing the development of Rayleigh-Taylor instability.

Keywords:

作者及机构信息

1.
南京理工大学, 瞬态物理全国重点实验室, 南京　210094

2.
中国工程物理研究院, 总体工程研究所, 绵阳　621999

3.
南京理工大学, 能源与动力学院, 南京　210094

通信作者: 张焕好, zhanghuanhao@njsut.edu.cn ; 陈志华, chenzh@njust.edu.cn ;

基金项目: 国家自然科学基金 (批准号: 12072162, 12102196, 12072334)、江苏省自然科学基金 (批准号: BK20210322)和中国博士后科学基金 (批准号: 2022M711642)资助的课题.

Authors and contacts

1.
National Key Laboratory of Transient Physics, Nanjing University of Science & Technology, Nanjing 210094, China

2.
Institute of Systems Engineering, China Academy of Engineering Physics, Mianyang 621999, China

3.
School of Energy and Power Engineering, Nanjing University of Science & Technology, Nanjing 210094, China

Corresponding author: Zhang Huan-Hao, zhanghuanhao@njsut.edu.cn ; Chen Zhi-Hua, chenzh@njust.edu.cn ;

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 12072162, 12102196, 12072334), the Natural Science Foundation of Jiangsu Province, China (Grant No. BK20210322), and the China Postdoctoral Science Foundation (Grant No. 2022M711642).

文章全文 : translate this paragraph

参考文献

[1]	Richtmyer R D 1960 Commun. Pure Appl. Math. 13 297 Google Scholar
[2]	Meshkov E E 1969 Fluid Dyn. 4 101
[3]	Kelvin L 1871 Philos. Mag. 42 362 Google Scholar
[4]	Helmholtz H V 1868 Monthly Reports of the Royal Prussian Academy of Philosophy in Berlin 23 215
[5]	Rayleigh L 1882 Proc. R. Math. Soc. s1-14 170 Google Scholar
[6]	Taylor S G 1950 Proc. R Soc. London Ser. A 201 192 Google Scholar
[7]	Zheng C, Zhang H H, Chen Z H, Wu W T, Sha S 2019 Phys. Fluids 31 086104 Google Scholar
[8]	林震亚, 张焕好, 陈志华, 刘迎 2017 爆炸与冲击 37 748 Google Scholar Lin Z Y, Zhang H H, Chen Z H, Liu Y 2017 Explo. Shock Waves 37 748 Google Scholar
[9]	Haas J F, Sturtevant B 1987 J. Fluid Mech. 181 41 Google Scholar
[10]	Jacobs J 1993 Phys. Fluids 5 2239 Google Scholar
[11]	Layes G, Metayer O L 2007 Phys. Fluids 19 042105 Google Scholar
[12]	Jacobs J and Krivets V 2005 Phys. Fluids 17 034105 Google Scholar
[13]	Zhai Z G, Wang M H, Si T, Luo X S 2014 J. Fluid Mech. 757 800 Google Scholar
[14]	Wang X S, Yang D G, Wu J Q, Luo X S 2015 Phys. Fluids 27 064104 Google Scholar
[15]	Bai J S, Zou L Y, Wang T, Liu K, Huang W B, Liu J G, Li P, Tan D W, Liu C L 2010 Phys. Rev. E 82 056318 Google Scholar
[16]	Si T, Long T, Zhai Z G, Luo X S 2015 J. Fluid Mech. 784 225 Google Scholar
[17]	Luo X S, Ding J C, Wang M H, Zhai Z G, Si T 2015 Phys. Fluids 27 091702 Google Scholar
[18]	Lei F, Ding J C, Si T, Zhai Z G, Luo X S 2017 J. Fluid Mech. 826 819 Google Scholar
[19]	Ding J C, Si T, Yang J M, Lu X Y, Zhai Z G, Luo X S 2017 Phys. Rev. Lett. 119 014501 Google Scholar
[20]	Liang Y, Ding J C, Zhai Z G, Si T, Luo X S 2017 Phys. Fluids 29 086101 Google Scholar
[21]	李冬冬, 王革, 张斌 2018 67 184702 Google Scholar Li D D, Wang G, Zhang B 2018 Acta Phys. Sin. 67 184702 Google Scholar
[22]	Guo X, Zhai Z G, Si T, Luo X S 2019 Phys. Rev. Fluids 4 092001(R
[23]	王显圣, 司廷, 罗喜盛, 杨基明 2012 力学学报 44 664 Google Scholar Wang X S, Si T, Luo X S, Yang J M 2012 Acta Mech. Sin. 44 664 Google Scholar
[24]	张升博, 张焕好, 陈志华, 郑纯 2023 72 105202 Google Scholar Zhang S B, Zhang H H, Chen Z H, Zheng C 2023 Acta Phys. Sin. 72 105202 Google Scholar
[25]	Zhang S B, Zhang H H, Chen Z H, Zheng C 2023 Phys. Plasmas 30 022107 Google Scholar
[26]	Samtaney R 2003 Phys. Fluids 15 53 Google Scholar
[27]	Wheatley V, Samtaney R, Pullin D I, Gehre R M 2014 Phys. Fluids 26 016102 Google Scholar
[28]	Sano T 2021 Astrophys. J. 920 29 Google Scholar
[29]	李源, 罗喜胜 2014 计算物理 31 659 Google Scholar Li Y, Luo X S 2014 Chin. J. Comput. Phys. 31 659 Google Scholar
[30]	Qiu Z Y, Wu Z W, Cao J T, Li D 2008 Phys. Plasmas 15 042305 Google Scholar
[31]	Tapinou K C, Wheatley V, Bond D, Jahn I 2023 Phys. Plasmas 30 022707 Google Scholar
[32]	Tapinou K C, Wheatley V, Bond D 2023 J. Fluid Mech. 977 A19 Google Scholar
[33]	Rinderknecht H G, Amendt P, Wilks S, Collins G 2018 Plasma Phys. Controlled Fusion 60 064001 Google Scholar
[34]	Xu A G, Zhang G C, Gan Y B, Chen F, Yu X J 2012 Front. Phys. 7 582 Google Scholar
[35]	Gan Y B, Xu A G, Lai H L, Li W, Sun G L, Succi S 2022 J. Fluid Mech. 951 A8 Google Scholar
[36]	Zhang D J, Xu A G, Zhang Y D, Gan Y B, Li Y J 2022 Phys. Fluids 34 086104 Google Scholar
[37]	Zhang Y D, Xu A G, Chen F, Lin C D, Wei Z H 2022 AIP Adv. 12 035347 Google Scholar
[38]	Song J H, Xu A G, Miao l, Chen F, Liu Z P, Wang L F, Wang N F, Hou X 2024 Phys. Fluids 36 016107 Google Scholar
[39]	沙莎, 张焕好, 陈志华, 郑纯, 吴威涛, 石启陈 2020 69 184701 Google Scholar Sha S, Zhang H H, Chen Z H, Zheng C, Wu W T, Shi Q C 2020 Acta Phys. Sin. 69 184701 Google Scholar
[40]	Zhang H H, Zheng C, Aubry N, Wu W T, Chen Z H 2020 Phys. Fluids 32 116104 Google Scholar
[41]	Colella P 1990 J. Comput. Phys. 87 171 Google Scholar
[42]	Londrillo P, Zanna L D 2004 J. Comput. Phys. 195 17 Google Scholar
[43]	Shin M, Stone J M, Snyder G F 2008 Astrophys. J. 680 336 Google Scholar
[44]	Saltzman J 1994 J. Comput. Phys. 115 153 Google Scholar
[45]	Colella P, Woodward P 1984 J. Comput. Phys. 54 17
[46]	Evans C, Hawley J 1988 Astrophys J. 322 659
[47]	Lin Z Y, Zhang H H, Chen Z H, Liu Y, Hong Y J 2017 Int. J. Comput. Fluid D. 31 21 Google Scholar
[48]	Giordano J, Burtschell Y 2006 Phys. Fluids. 18 036102 Google Scholar

施引文献

图 1 (a) 仿真模型; (b) 氦气组分沿y = 0的分布

Fig. 1. (a) Simulation model; (b) distribution of helium components along y = 0.

下载: 全尺寸图片幻灯片

图 2 平面激波与He气柱作用过程的计算结果(下)与相关实验结果^[9](上)的对比

Fig. 2. Comparison between simulation results of this study (down) and experimental results ^[9] (up) for the interaction between a shock wave and a helium gas cylinder.

下载: 全尺寸图片幻灯片

图 3 无磁场控制下, 激波冲击He气柱过程的阴影图

Fig. 3. Shadowgraph images for the interaction of a shock wave with a helium cylinder in HD condition.

下载: 全尺寸图片幻灯片

图 4 流向磁场作用下, 激波冲击He气柱过程的阴影图

Fig. 4. Shadowgraph images for interaction of a shock wave with a helium cylinder in the presence of a transverse magnetic field.

下载: 全尺寸图片幻灯片

图 5 纵向磁场作用下, 激波冲击He气柱过程的阴影图

Fig. 5. Shadowgraph images for the interaction of a shock wave with a helium cylinder in the presence of a longitudinal magnetic field.

下载: 全尺寸图片幻灯片

图 6 不同磁场方向下的流场涡量分布

Fig. 6. Vorticity contour in RMI under various magnetic-field directions.

下载: 全尺寸图片幻灯片

图 7 环量随时间的变化曲线　(a) 正环量Γ₊; (b) 负环量Γ_–; (c) 总环量Γ

Fig. 7. History of the circulation: (a) Positive circulation Γ₊; (b) negative circulation Γ_–; (c) total circulation Γ.

下载: 全尺寸图片幻灯片

图 8 激波冲击氦气柱过程中气柱特征尺寸的变化曲线　(a)气柱长度L; (b)气柱高度H; (c)中轴宽度W

Fig. 8. The variation curves of characteristic dimensions of helium cylinder during the interaction process with the shock wave: (a) Length of helium cylinder, L; (b) height of helium cylinder, H; (c) axis width of helium cylinder, W.

下载: 全尺寸图片幻灯片

图 9 不同磁场方向下, He气柱体积压缩率V(t)/V(0)变化

Fig. 9. Volume compressibility of He cylinder for various magnetic-field directions.

下载: 全尺寸图片幻灯片

图 10 流场能量随时间的变化曲线　(a) 总能E、内能E_p ; (b) 磁能E_b; (c) 横向总动能E_kx; (d) 纵向总动能E_ky

Fig. 10. Time history of the flow energy: (a) Total energy E, internal energy E_p; (b) magnetic energy E_b; (c) lateral total kinetic energy E_kx; (d) vertical total kinetic energy E_ky.

下载: 全尺寸图片幻灯片

图 11 内能分布随时间的变化

Fig. 11. Distribution of internal energy over time.

下载: 全尺寸图片幻灯片

图 12 t = 0.15 ms时, 流场磁场强度与磁能量的分布云图

Fig. 12. The distribution of magnetic field strength and magnetic energy in the flow field at t = 0.15 ms.

下载: 全尺寸图片幻灯片

图 13 氦气柱附近速度矢量分布图

Fig. 13. Velocity vector distribution near the He cylinder.

下载: 全尺寸图片幻灯片

图 14 涡量层上的磁张力和磁压力分布

Fig. 14. Magnetic tension and magnetic pressure distributions on the vorticity layers.

下载: 全尺寸图片幻灯片

图 15 纵向动能分布(upper)和涡量(lower)对照图

Fig. 15. Comparison of longitudinal kinetic energy distribution (upper) with vorticity (lower).

下载: 全尺寸图片幻灯片

表 1 气体参数

Table 1. Gas parameters.

Gas Density
ρ/(kg·m^–3) Specific-heat ratio γ Molar mass
M/(g·mol^–1) Speed of sound
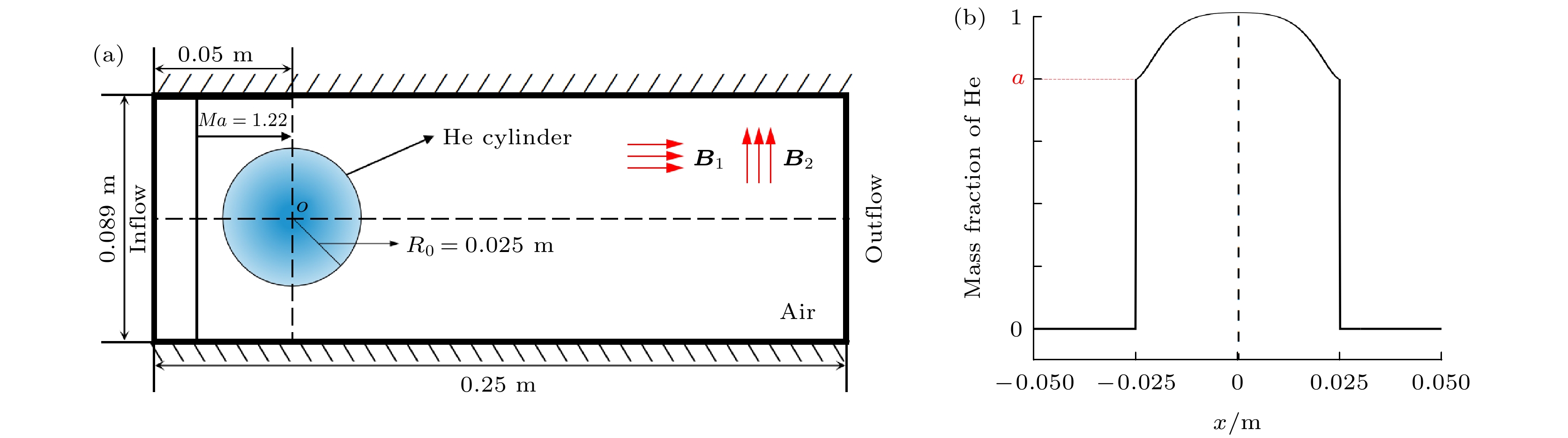
c_A/(m·s^–1)

Air 1.176 1.40 28.96 347

He 0.162 1.67 4.00 1021

下载: 导出CSV

表 2 不同工况下的初始条件

Table 2. The initial conditions of different cases.

Case a $\beta^{-1}$ Magnetic field direction

1 0.8 0 —

2 0.8 0.0005 Transverse

3 0.8 0.0005 Longitudinal

下载: 导出CSV

map

[1]	Richtmyer R D 1960 Commun. Pure Appl. Math. 13 297 Google Scholar
[2]	Meshkov E E 1969 Fluid Dyn. 4 101
[3]	Kelvin L 1871 Philos. Mag. 42 362 Google Scholar
[4]	Helmholtz H V 1868 Monthly Reports of the Royal Prussian Academy of Philosophy in Berlin 23 215
[5]	Rayleigh L 1882 Proc. R. Math. Soc. s1-14 170 Google Scholar
[6]	Taylor S G 1950 Proc. R Soc. London Ser. A 201 192 Google Scholar
[7]	Zheng C, Zhang H H, Chen Z H, Wu W T, Sha S 2019 Phys. Fluids 31 086104 Google Scholar
[8]	林震亚, 张焕好, 陈志华, 刘迎 2017 爆炸与冲击 37 748 Google Scholar Lin Z Y, Zhang H H, Chen Z H, Liu Y 2017 Explo. Shock Waves 37 748 Google Scholar
[9]	Haas J F, Sturtevant B 1987 J. Fluid Mech. 181 41 Google Scholar
[10]	Jacobs J 1993 Phys. Fluids 5 2239 Google Scholar
[11]	Layes G, Metayer O L 2007 Phys. Fluids 19 042105 Google Scholar
[12]	Jacobs J and Krivets V 2005 Phys. Fluids 17 034105 Google Scholar
[13]	Zhai Z G, Wang M H, Si T, Luo X S 2014 J. Fluid Mech. 757 800 Google Scholar
[14]	Wang X S, Yang D G, Wu J Q, Luo X S 2015 Phys. Fluids 27 064104 Google Scholar
[15]	Bai J S, Zou L Y, Wang T, Liu K, Huang W B, Liu J G, Li P, Tan D W, Liu C L 2010 Phys. Rev. E 82 056318 Google Scholar
[16]	Si T, Long T, Zhai Z G, Luo X S 2015 J. Fluid Mech. 784 225 Google Scholar
[17]	Luo X S, Ding J C, Wang M H, Zhai Z G, Si T 2015 Phys. Fluids 27 091702 Google Scholar
[18]	Lei F, Ding J C, Si T, Zhai Z G, Luo X S 2017 J. Fluid Mech. 826 819 Google Scholar
[19]	Ding J C, Si T, Yang J M, Lu X Y, Zhai Z G, Luo X S 2017 Phys. Rev. Lett. 119 014501 Google Scholar
[20]	Liang Y, Ding J C, Zhai Z G, Si T, Luo X S 2017 Phys. Fluids 29 086101 Google Scholar
[21]	李冬冬, 王革, 张斌 2018 67 184702 Google Scholar Li D D, Wang G, Zhang B 2018 Acta Phys. Sin. 67 184702 Google Scholar
[22]	Guo X, Zhai Z G, Si T, Luo X S 2019 Phys. Rev. Fluids 4 092001(R
[23]	王显圣, 司廷, 罗喜盛, 杨基明 2012 力学学报 44 664 Google Scholar Wang X S, Si T, Luo X S, Yang J M 2012 Acta Mech. Sin. 44 664 Google Scholar
[24]	张升博, 张焕好, 陈志华, 郑纯 2023 72 105202 Google Scholar Zhang S B, Zhang H H, Chen Z H, Zheng C 2023 Acta Phys. Sin. 72 105202 Google Scholar
[25]	Zhang S B, Zhang H H, Chen Z H, Zheng C 2023 Phys. Plasmas 30 022107 Google Scholar
[26]	Samtaney R 2003 Phys. Fluids 15 53 Google Scholar
[27]	Wheatley V, Samtaney R, Pullin D I, Gehre R M 2014 Phys. Fluids 26 016102 Google Scholar
[28]	Sano T 2021 Astrophys. J. 920 29 Google Scholar
[29]	李源, 罗喜胜 2014 计算物理 31 659 Google Scholar Li Y, Luo X S 2014 Chin. J. Comput. Phys. 31 659 Google Scholar
[30]	Qiu Z Y, Wu Z W, Cao J T, Li D 2008 Phys. Plasmas 15 042305 Google Scholar
[31]	Tapinou K C, Wheatley V, Bond D, Jahn I 2023 Phys. Plasmas 30 022707 Google Scholar
[32]	Tapinou K C, Wheatley V, Bond D 2023 J. Fluid Mech. 977 A19 Google Scholar
[33]	Rinderknecht H G, Amendt P, Wilks S, Collins G 2018 Plasma Phys. Controlled Fusion 60 064001 Google Scholar
[34]	Xu A G, Zhang G C, Gan Y B, Chen F, Yu X J 2012 Front. Phys. 7 582 Google Scholar
[35]	Gan Y B, Xu A G, Lai H L, Li W, Sun G L, Succi S 2022 J. Fluid Mech. 951 A8 Google Scholar
[36]	Zhang D J, Xu A G, Zhang Y D, Gan Y B, Li Y J 2022 Phys. Fluids 34 086104 Google Scholar
[37]	Zhang Y D, Xu A G, Chen F, Lin C D, Wei Z H 2022 AIP Adv. 12 035347 Google Scholar
[38]	Song J H, Xu A G, Miao l, Chen F, Liu Z P, Wang L F, Wang N F, Hou X 2024 Phys. Fluids 36 016107 Google Scholar
[39]	沙莎, 张焕好, 陈志华, 郑纯, 吴威涛, 石启陈 2020 69 184701 Google Scholar Sha S, Zhang H H, Chen Z H, Zheng C, Wu W T, Shi Q C 2020 Acta Phys. Sin. 69 184701 Google Scholar
[40]	Zhang H H, Zheng C, Aubry N, Wu W T, Chen Z H 2020 Phys. Fluids 32 116104 Google Scholar
[41]	Colella P 1990 J. Comput. Phys. 87 171 Google Scholar
[42]	Londrillo P, Zanna L D 2004 J. Comput. Phys. 195 17 Google Scholar
[43]	Shin M, Stone J M, Snyder G F 2008 Astrophys. J. 680 336 Google Scholar
[44]	Saltzman J 1994 J. Comput. Phys. 115 153 Google Scholar
[45]	Colella P, Woodward P 1984 J. Comput. Phys. 54 17
[46]	Evans C, Hawley J 1988 Astrophys J. 322 659
[47]	Lin Z Y, Zhang H H, Chen Z H, Liu Y, Hong Y J 2017 Int. J. Comput. Fluid D. 31 21 Google Scholar
[48]	Giordano J, Burtschell Y 2006 Phys. Fluids. 18 036102 Google Scholar

[1]	张升博, 张焕好, 陈志华, 郑纯. 不同界面组分分布对Richtmyer-Meshkov不稳定性的影响. , 2023, 72(10): 105202. doi: 10.7498/aps.72.20222090
[2]	党子涵, 郑纯, 张焕好, 陈志华. 汇聚激波诱导具有正弦扰动双层重气柱界面的演化机理. , 2022, 71(21): 214703. doi: 10.7498/aps.71.20221012
[3]	罗仕超, 吴里银, 常雨. 高超声速湍流流动磁流体动力学控制机理. , 2022, 71(21): 214702. doi: 10.7498/aps.71.20220941
[4]	范海龙, 陈明文. 磁场对二元合金凝固过程中糊状层稳定性的影响. , 2021, 70(6): 066401. doi: 10.7498/aps.70.20201748
[5]	袁永腾, 涂绍勇, 尹传盛, 李纪伟, 戴振生, 杨正华, 侯立飞, 詹夏宇, 晏骥, 董云松, 蒲昱东, 邹士阳, 杨家敏, 缪文勇. 冲击波波后辐射效应对Richtmyer-Meshkov不稳定性增长影响的实验研究. , 2021, 70(20): 205203. doi: 10.7498/aps.70.20210653
[6]	沙莎, 张焕好, 陈志华, 郑纯, 吴威涛, 石启陈. 纵向磁场抑制Richtmyer-Meshkov不稳定性机理. , 2020, 69(18): 184701. doi: 10.7498/aps.69.20200363
[7]	刘迎, 陈志华, 郑纯. 黏性各向异性磁流体Kelvin-Helmholtz不稳定性: 二维数值研究. , 2019, 68(3): 035201. doi: 10.7498/aps.68.20181747
[8]	董国丹, 郭则庆, 秦建华, 张焕好, 姜孝海, 陈志华, 沙莎. 不同磁场构型下Richtmyer-Meshkov不稳定性的数值研究及动态模态分解. , 2019, 68(16): 165201. doi: 10.7498/aps.68.20190410
[9]	李冬冬, 王革, 张斌. 激波作用不同椭圆氦气柱过程中流动混合研究. , 2018, 67(18): 184702. doi: 10.7498/aps.67.20180879
[10]	董国丹, 张焕好, 林震亚, 秦建华, 陈志华, 郭则庆, 沙莎. 磁控条件下激波冲击三角形气柱过程的数值研究. , 2018, 67(20): 204701. doi: 10.7498/aps.67.20181127
[11]	李俊涛, 孙宇涛, 胡晓棉, 任玉新. 激波冲击V形界面重气体导致的壁面与旋涡作用及其对湍流混合的影响. , 2017, 66(23): 235201. doi: 10.7498/aps.66.235201
[12]	李俊涛, 孙宇涛, 潘建华, 任玉新. 冲击加载下V形界面的失稳与湍流混合. , 2016, 65(24): 245202. doi: 10.7498/aps.65.245202
[13]	沙莎, 陈志华, 张庆兵. 激波与SF6球形气泡相互作用的数值研究. , 2015, 64(1): 015201. doi: 10.7498/aps.64.015201
[14]	陈植, 易仕和, 朱杨柱, 何霖, 全鹏程. 强梯度复杂流场中的粒子动力学响应试验研究. , 2014, 63(18): 188301. doi: 10.7498/aps.63.188301
[15]	郑伟花, 贾虎. 水下高斯界面背向散射超声散斑场的相位奇异. , 2014, 63(5): 054301. doi: 10.7498/aps.63.054301
[16]	沙莎, 陈志华, 薛大文, 张辉. 激波与SF6梯形气柱相互作用的数值模拟. , 2014, 63(8): 085205. doi: 10.7498/aps.63.085205
[17]	沙莎, 陈志华, 薛大文. 激波冲击R22重气柱所导致的射流与混合研究. , 2013, 62(14): 144701. doi: 10.7498/aps.62.144701
[18]	霍新贺, 王立锋, 陶烨晟, 李英骏. 非理想流体中Rayleigh-Taylor和Richtmyer-Meshkov不稳定性气泡速度研究. , 2013, 62(14): 144705. doi: 10.7498/aps.62.144705
[19]	陶烨晟, 王立锋, 叶文华, 张广财, 张建成, 李英骏. 任意Atwood数Rayleigh-Taylor和 Richtmyer-Meshkov 不稳定性气泡速度研究. , 2012, 61(7): 075207. doi: 10.7498/aps.61.075207
[20]	王健, 李应红, 程邦勤, 苏长兵, 宋慧敏, 吴云. 等离子体气动激励控制激波的机理研究. , 2009, 58(8): 5513-5519. doi: 10.7498/aps.58.5513

计量

文章访问数: 2393
PDF下载量: 33
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

激波与轻质气柱作用过程的磁场抑制特性