-
基于计算流体力学平台OpenFOAM, 本文开发了一套可压缩磁流体求解器, 并将其应用于二维和三维的跨音速束流模拟. 该求解器对OpenFOAM自带的密度基中心差分黎曼求解器rhoCentralFoam进行了修改, 植入一个隐式压力分离算法用以控制磁场散度误差并保证模拟结果的数值精度. 本文对此求解器进行了检测, 证明了它的收敛阶在1—2之间, 并将其应用到强激光等离子体的磁流体模拟. 利用该求解器, 本文讨论了外加均匀轴向磁场对激光等离子体喷流的影响, 发现了喷嘴和结节位置与热压比开方之间的线性关系. 本文还分析了电容线圈中产生的非均匀磁场对激光等离子体喷流的影响. 初步模拟结果表明, 当线圈中心磁场相同时, 小尺寸线圈产生的磁场会加快喷嘴和结节的形成, 等效的均匀轴向磁场更大. 此模拟结果可以作为我们将来的磁化喷流实验的参考. 同时, 这样物理结果表明该磁流体求解器适合做面向激光等离子体实验的工程计算, 可以应对构型比较复杂的场合.
-
关键词:
- 可压缩磁流体力学求解器 /
- 计算流体力学 /
- OpenFOAM程序 /
- 强激光等离子体 /
- 磁流体模拟
We develop a compressible magnetohydrodynamic solver to simulate the transonic flows based on an open-source computational fluid dynamics platform OpenFOAM. The solver is achieved by modifying the density-based Riemann solver rhoCentralFoam which adopts a central scheme and is available in OpenFOAM. To improve simulation accuracy and avoid non-physical oscillations, a specialized pressure-implicit algorithm with the splitting of operators is implemented to guarantee the incompressibility of magnetic field. The solver is benchmarked and the convergence rate is between the first and the second order. After benchmark, we apply this solver to magnetohydrodynamic simulations of intense-laser-produced plasma. The influences of uniform axial magnetic field and nonuniform coil-current-induced magnetic field on laser-produced plasma jets are investigated. With the uniform axial magnetic field, the positions of nozzle and the distance between knots are linearly related to square root of thermal over magnetic pressure. With the nonuniform magnetic field generated in the coil, knots are nonlinearly distributed in space and the nozzle position is modulated according to preliminary simulations. In the two kinds of magnetic fields, when the B-field strength is the same at coil center, the magnetic field of relatively small coils can shorten the times of forming nozzles and knots, suggesting that the coil magnetic field is equivalent to a higher uniform one. The simulations can be used as a reference for our future experiment on magnetized laser-produced plasma jet. Meanwhile, our simulation investigation shows that this magnetohydrodynamic solver is suitable for engineering calculation for laser plasma experiments and can deal with the situation with relatively complex configurations.-
Keywords:
- compressible magnetohydrodynamic solver /
- computational fluid dynamics /
- OpenFOAM code /
- intense-laser-produced plasma /
- magnetohydrodynamic simulation
[1] Gotchev O V, Chang P Y, Knauer J P, Meyerhofer D D, Polomarov O, Frenje J, Li C K, Manuel M J, Petrasso R D, Rygg J R, Seguin F H, Betti R 2009 Phys. Rev. Lett. 103 215004
Google Scholar
[2] Chang P Y, Fiksel G, Hohenberger M, Knauer J P, Betti R, Marshall F J, Meyerhofer D D, Seguin F H, Petrasso R D 2011 Phys. Rev. Lett. 107 035006
Google Scholar
[3] Ciardi A, Vinci T, Fuchs J, Albertazzi B, Riconda C, Pepin H, Portugall O 2013 Phys. Rev. Lett. 110 025002
Google Scholar
[4] Higginson D P, Khiar B, Revet G, Beard J, Blecher M, Borghesi M, Burdonov K, Chen S N, Filippov E, Khaghani D, Naughton K, Pepin H, Pikuz S, Portugall O, Riconda C, Riquier R, Rodriguez R, Ryazantsev S N, Skobelev I Y, Soloviev A, Starodubtsev M, Vinci T, Willi O, Ciardi A, Fuchs J 2017 Phys. Rev. Lett. 119 255002
Google Scholar
[5] Revet G, Khiar B, Filippov E, Argiroffi C, Beard J, Bonito R, Cerchez M, Chen S N, Gangolf T, Higginson D P, Mignone A, Olmi B, Ouille M, Ryazantsev S N, Skobelev I Y, Safronova M I, Starodubtsev M, Vinci T, Willi O, Pikuz S, Orlando S, Ciardi A, Fuchs J 2021 Nat. commun. 12 762
Google Scholar
[6] Muranaka T, Uchimura H, Nakashima H, Zakharov Y P, Nikitin S A, Ponomarenko A G 2001 Jpn. J. Appl. Phys. 40 824
Google Scholar
[7] Plechaty C, Presura R, Esaulov A A 2013 Phys. Rev. Lett. 111 185002
Google Scholar
[8] Albertazzi B, Ciardi A, Nakatsutsumi M, Vinci T, Beard J, Bonito R, Billette J, Borghesi M, Burkley Z, Chen S N, Cowan T E, Herrmannsdorfer T, Higginson D P, Kroll F, Pikuz S A, Naughton K, Romagnani L, Riconda C, Revet G, Riquier R, Schlenvoigt H P, Skobelev I Y, Faenov A Y, Soloviev A, Huarte-Espinosa M, Frank A, Portugall O, Pepin H, Fuchs J 2014 Science 346 325
Google Scholar
[9] Ivanov V V, Maximov A V, Betti R, Wiewior P P, Hakel P, Sherrill M E 2017 Plasma Phys. Contr. F. 59 085008
Google Scholar
[10] Dubey A, Antypas K, Ganapathy M K, Reid L B, Riley K, Sheeler D, Siegel A, Weide K 2009 Parallel Comput. 35 512
Google Scholar
[11] Ciardi A, Lebedev S V, Frank A, Blackman E G, Chittenden J P, Jennings C J, Ampleford D J, Bland S N, Bott S C, Rapley J, Hall G N, Suzuki-Vidal F A, Marocchino A, Lery T, Stehle C 2007 Phys. Plasmas 14 056501
Google Scholar
[12] Seyler C E, Martin M R 2011 Phys. Plasmas 18 012703
Google Scholar
[13] Ryutov D D 2010 Astrophys. Space Sci. 336 21
Google Scholar
[14] Kostyukov I Y, Ryzhkov S V 2011 Plasma Phys. Rep. 37 1092
Google Scholar
[15] Weller H G, Tabor G, Jasak H, Fureby C 1998 Comput. Phys. 12 620
Google Scholar
[16] Singh R J, Gohil T B 2019 Int. J. Therm. Sci. 146 106096
Google Scholar
[17] Xisto C, Páscoa J, Oliveira P, Nicolini D 2010 European Conference on Computational Fluid Dynamics Lisbon, Portugal, June 14–17, 2010
[18] Ryakhovskiy A I, Schmidt A A 2017 J. Phys. Conf. Ser. 929 012098
Google Scholar
[19] Chelem Mayigué C, Groll R 2016 Arch. Appl. Mech. 87 667
Google Scholar
[20] Kurganov A, Noelle S, Petrova G 2001 SIAM J. Sci. Comput. 23 707
Google Scholar
[21] Kurganov A, Tadmor E 2000 J. Comput. Phys. 160 241
Google Scholar
[22] Kühn C, Groll R 2021 Comput. Phys. Commun. 262 107853
Google Scholar
[23] Brackbill J U, Barnes D C 1980 J. Comput. Phys. 35 426
Google Scholar
[24] Orszag S A, Tang C-M 1979 J. Fluid Mech. 90 129
Google Scholar
[25] FLASH User’s Guide Version 4.5, flash. uchicago. edu/ site/publications/flash_pubs. shtml [2017-12-18]
[26] Ziegler U 2008 Comput. Phys. Commun. 179 227
Google Scholar
[27] Fogang F, Tchuen G, Burtschell Y, Woafo P 2015 Comput. Fluids 114 297
Google Scholar
[28] Balsara D S, Spicer D S 1999 J. Comput. Phys. 153 671
Google Scholar
[29] Lei Z, Zhao Z H, Yao W P, Xie Y, Jiao J L, Zhou C T, Zhu S P, He X T, Qiao B 2020 Plasma Phys. Contr. F. 62 095020
Google Scholar
[30] Fujioka S, Zhang Z, Ishihara K, Shigemori K, Hironaka Y, Johzaki T, Sunahara A, Yamamoto N, Nakashima H, Watanabe T, Shiraga H, Nishimura H, Azechi H 2013 Sci. Rep. 3 1170
Google Scholar
-
图 2 奥萨格-唐磁流体涡旋的(a)初始速度场和(b)初始磁场
Fig. 2. Initialization of speed field (a) and magnetic field (b) in Orszag-Tang MHD vortex.
图 3 t = 0.5时奥萨格-唐磁流体涡旋的模拟结果 (a), (c) y = 0.25处密度和磁场比较; (b), (d) 密度和磁场廓线
Fig. 3. Simulation results of Orszag-Tang MHD vortex at t = 0.5: (a), (c) 1D cut comparisons of density and B-field at y = 0.25; (b), (d) density and B-field contours.
图 4 磁流体转子 (a) 初始密度廓线; (b), (c) t = 0.15时密度和磁场廓线; (d) t = 0.15时x = 0处磁场比较
Fig. 4. MHD rotor: (a) Initial density contours; (b), (c) density and magnetic field contours at t = 0.15; (c) 1D cut comparisons of B-field at x = 0 at t = 0.15.
图 5 t = 0.15时MHDFoam求解磁流体转子问题的磁场散度误差
Fig. 5. Divergence of magnetic fields using the MHDFoam solver at t = 0.15 for the MHD rotor problem.
图 7 t = 22 ns时均匀磁场下的密度廓线
Fig. 7. Density contours at uniform magnetic fields at t = 22 ns
图 8 (a) t = 22 ns时轴线密度分布; (b), (c)参数L和S与
$ \beta_{\rm o}^{1/2} $ 关系Fig. 8. (a) Density distributions at axis at t = 22 ns; (b), (c) parameter L and S as a function of
$ \beta_{\rm o}^{1/2} $ 
图 9 线圈电流磁场 (a) xz平面二维分布; (b) x = 0处分布; (c) z = 0处分布
Fig. 9. Magnetic field of coil currents: (a) 2D distributions in the xz-plane; (b) 1D cut at x = 0; (c) 1D cut at z = 0.
图 10 t = 22 ns时图9配置的非均匀磁场条件下的密度廓线及与均匀磁场的比对
Fig. 10. Density contours at nonuniform magnetic fields set in Fig. 9 at t = 22 ns compared with uniform magnetic fields.
图 11 t = 22 ns时模拟结果 (a)轴线密度分布; (b)无量纲参数S/D在Ia相平面上的分布
Fig. 11. Simulation results at t = 22 ns: (a) Density distributions at axis; (b) dimensionless parameter S/D in the Ia-plane.
表 1 奥萨格-唐问题的相对误差和收敛阶数
Table 1. Relative errors (δN) and convergence order (RN) for Orszag-Tang problem.
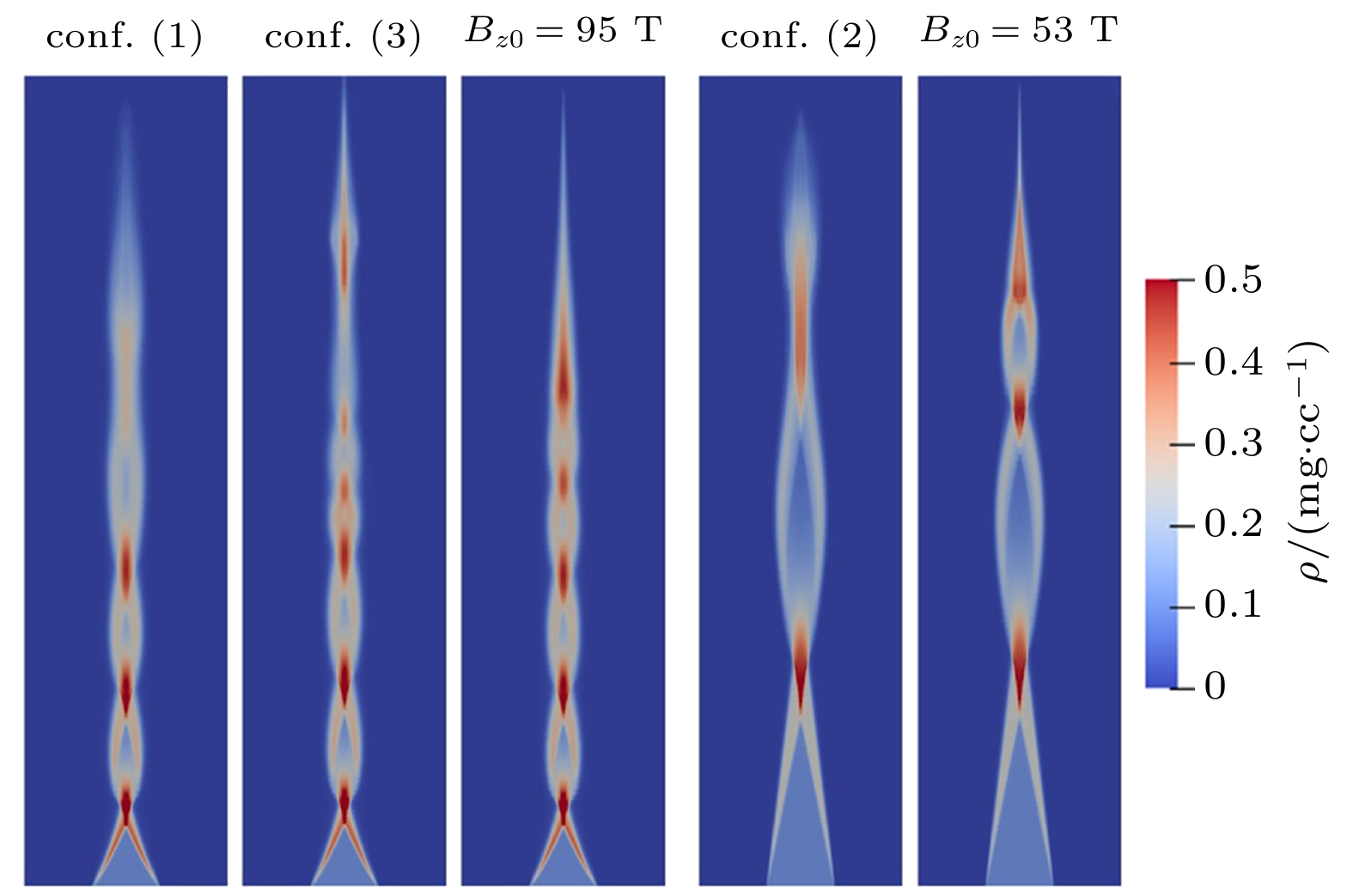
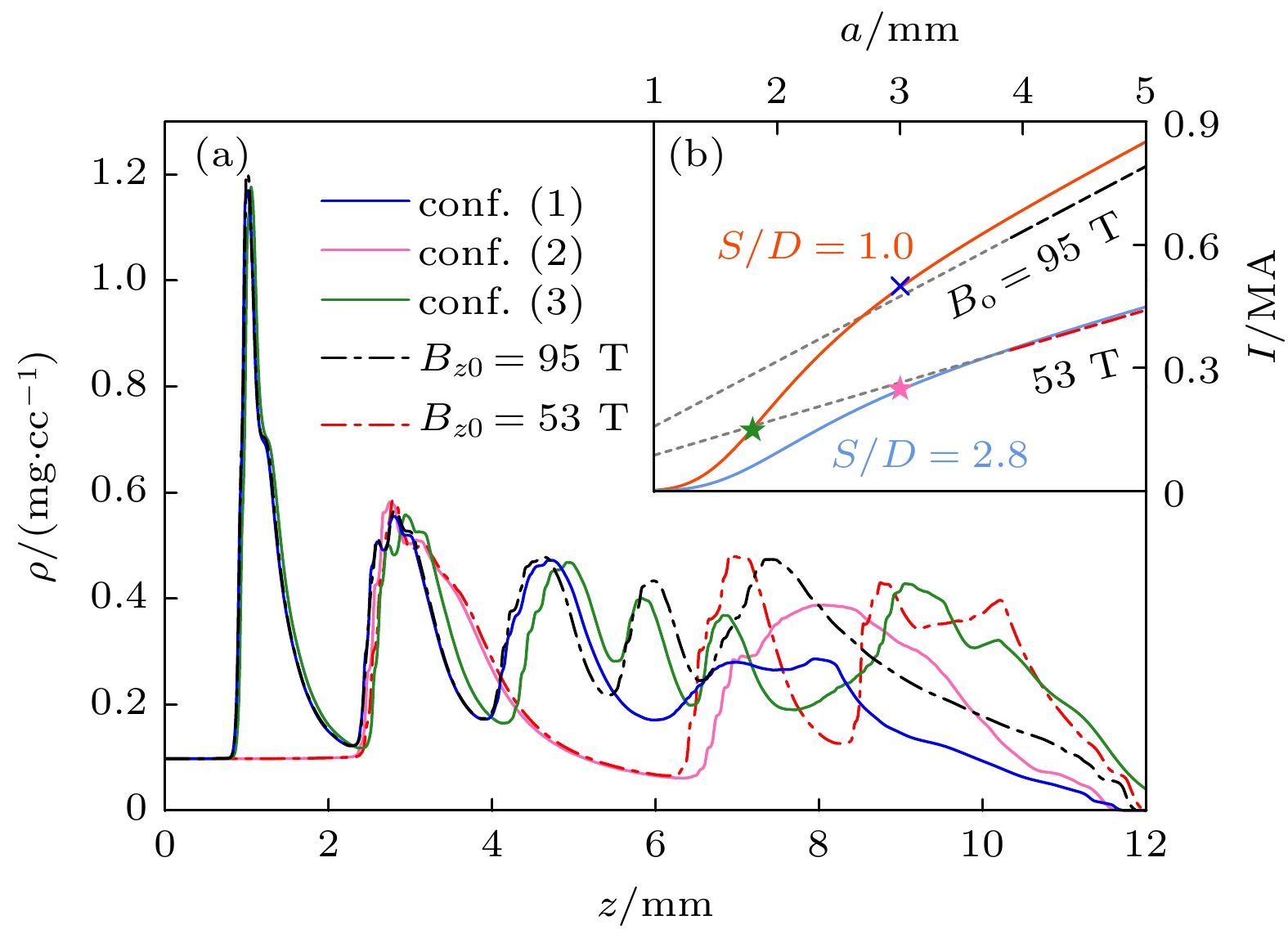
N MHDFoam KT-MHD[19] δN RN δN RN 50 0.15005 — 0.30370 — 100 0.08024 0.90 0.16383 0.89 200 0.03554 1.17 0.08065 1.02 300 0.02062 1.34 0.04604 1.38 400 0.01393 1.36 0.02875 1.49 
下载: 导出CSV
非均匀线圈磁场构型 等效参数 Be/T λe/mm 构型(1) ($I = 0.5{\text{ MA}}$, $a = 3.0{\text{ mm}}$, ${B_{\text{o}}} = 104.7{\text{ T}}$) ~ 95 ~ 5 构型(2) ($I = 0.25{\text{ MA}}$, $a = 3.0{\text{ mm}}$, ${B_{\text{o}}} = 52.4{\text{ T}}$) ~ 53 ~ 6.5 构型(3) ($I = 0.15{\text{ MA}}$, $a = 1.8{\text{ mm}}$, ${B_{\text{o}}} = 52.4{\text{ T}}$) ~ 95 ~ 6
下载: 导出CSV
-
[1] Gotchev O V, Chang P Y, Knauer J P, Meyerhofer D D, Polomarov O, Frenje J, Li C K, Manuel M J, Petrasso R D, Rygg J R, Seguin F H, Betti R 2009 Phys. Rev. Lett. 103 215004
Google Scholar
[2] Chang P Y, Fiksel G, Hohenberger M, Knauer J P, Betti R, Marshall F J, Meyerhofer D D, Seguin F H, Petrasso R D 2011 Phys. Rev. Lett. 107 035006
Google Scholar
[3] Ciardi A, Vinci T, Fuchs J, Albertazzi B, Riconda C, Pepin H, Portugall O 2013 Phys. Rev. Lett. 110 025002
Google Scholar
[4] Higginson D P, Khiar B, Revet G, Beard J, Blecher M, Borghesi M, Burdonov K, Chen S N, Filippov E, Khaghani D, Naughton K, Pepin H, Pikuz S, Portugall O, Riconda C, Riquier R, Rodriguez R, Ryazantsev S N, Skobelev I Y, Soloviev A, Starodubtsev M, Vinci T, Willi O, Ciardi A, Fuchs J 2017 Phys. Rev. Lett. 119 255002
Google Scholar
[5] Revet G, Khiar B, Filippov E, Argiroffi C, Beard J, Bonito R, Cerchez M, Chen S N, Gangolf T, Higginson D P, Mignone A, Olmi B, Ouille M, Ryazantsev S N, Skobelev I Y, Safronova M I, Starodubtsev M, Vinci T, Willi O, Pikuz S, Orlando S, Ciardi A, Fuchs J 2021 Nat. commun. 12 762
Google Scholar
[6] Muranaka T, Uchimura H, Nakashima H, Zakharov Y P, Nikitin S A, Ponomarenko A G 2001 Jpn. J. Appl. Phys. 40 824
Google Scholar
[7] Plechaty C, Presura R, Esaulov A A 2013 Phys. Rev. Lett. 111 185002
Google Scholar
[8] Albertazzi B, Ciardi A, Nakatsutsumi M, Vinci T, Beard J, Bonito R, Billette J, Borghesi M, Burkley Z, Chen S N, Cowan T E, Herrmannsdorfer T, Higginson D P, Kroll F, Pikuz S A, Naughton K, Romagnani L, Riconda C, Revet G, Riquier R, Schlenvoigt H P, Skobelev I Y, Faenov A Y, Soloviev A, Huarte-Espinosa M, Frank A, Portugall O, Pepin H, Fuchs J 2014 Science 346 325
Google Scholar
[9] Ivanov V V, Maximov A V, Betti R, Wiewior P P, Hakel P, Sherrill M E 2017 Plasma Phys. Contr. F. 59 085008
Google Scholar
[10] Dubey A, Antypas K, Ganapathy M K, Reid L B, Riley K, Sheeler D, Siegel A, Weide K 2009 Parallel Comput. 35 512
Google Scholar
[11] Ciardi A, Lebedev S V, Frank A, Blackman E G, Chittenden J P, Jennings C J, Ampleford D J, Bland S N, Bott S C, Rapley J, Hall G N, Suzuki-Vidal F A, Marocchino A, Lery T, Stehle C 2007 Phys. Plasmas 14 056501
Google Scholar
[12] Seyler C E, Martin M R 2011 Phys. Plasmas 18 012703
Google Scholar
[13] Ryutov D D 2010 Astrophys. Space Sci. 336 21
Google Scholar
[14] Kostyukov I Y, Ryzhkov S V 2011 Plasma Phys. Rep. 37 1092
Google Scholar
[15] Weller H G, Tabor G, Jasak H, Fureby C 1998 Comput. Phys. 12 620
Google Scholar
[16] Singh R J, Gohil T B 2019 Int. J. Therm. Sci. 146 106096
Google Scholar
[17] Xisto C, Páscoa J, Oliveira P, Nicolini D 2010 European Conference on Computational Fluid Dynamics Lisbon, Portugal, June 14–17, 2010
[18] Ryakhovskiy A I, Schmidt A A 2017 J. Phys. Conf. Ser. 929 012098
Google Scholar
[19] Chelem Mayigué C, Groll R 2016 Arch. Appl. Mech. 87 667
Google Scholar
[20] Kurganov A, Noelle S, Petrova G 2001 SIAM J. Sci. Comput. 23 707
Google Scholar
[21] Kurganov A, Tadmor E 2000 J. Comput. Phys. 160 241
Google Scholar
[22] Kühn C, Groll R 2021 Comput. Phys. Commun. 262 107853
Google Scholar
[23] Brackbill J U, Barnes D C 1980 J. Comput. Phys. 35 426
Google Scholar
[24] Orszag S A, Tang C-M 1979 J. Fluid Mech. 90 129
Google Scholar
[25] FLASH User’s Guide Version 4.5, flash. uchicago. edu/ site/publications/flash_pubs. shtml [2017-12-18]
[26] Ziegler U 2008 Comput. Phys. Commun. 179 227
Google Scholar
[27] Fogang F, Tchuen G, Burtschell Y, Woafo P 2015 Comput. Fluids 114 297
Google Scholar
[28] Balsara D S, Spicer D S 1999 J. Comput. Phys. 153 671
Google Scholar
[29] Lei Z, Zhao Z H, Yao W P, Xie Y, Jiao J L, Zhou C T, Zhu S P, He X T, Qiao B 2020 Plasma Phys. Contr. F. 62 095020
Google Scholar
[30] Fujioka S, Zhang Z, Ishihara K, Shigemori K, Hironaka Y, Johzaki T, Sunahara A, Yamamoto N, Nakashima H, Watanabe T, Shiraga H, Nishimura H, Azechi H 2013 Sci. Rep. 3 1170
Google Scholar
下载:
计量
- 文章访问数: 5930
- PDF下载量: 169
- 被引次数: 0
