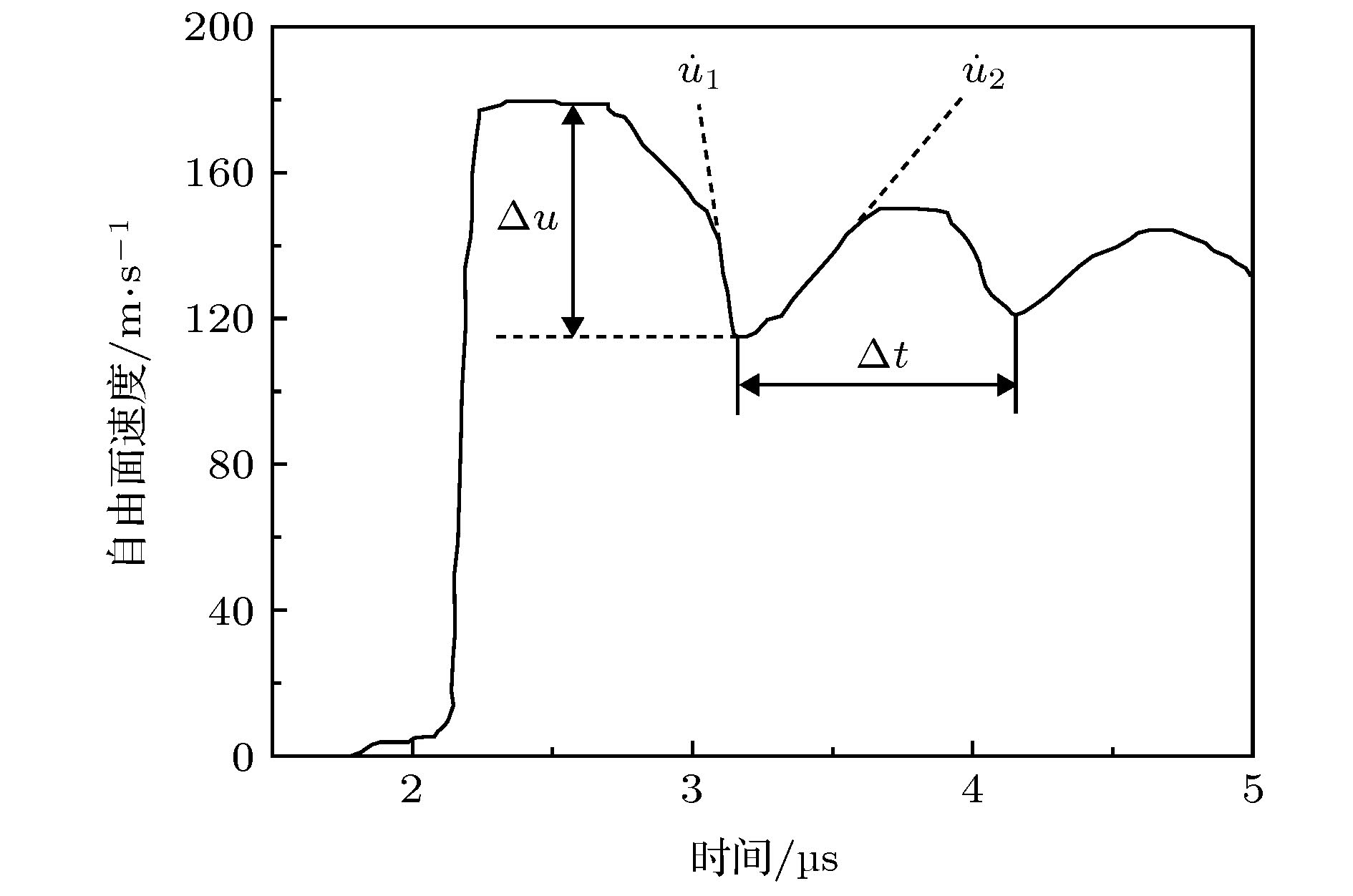
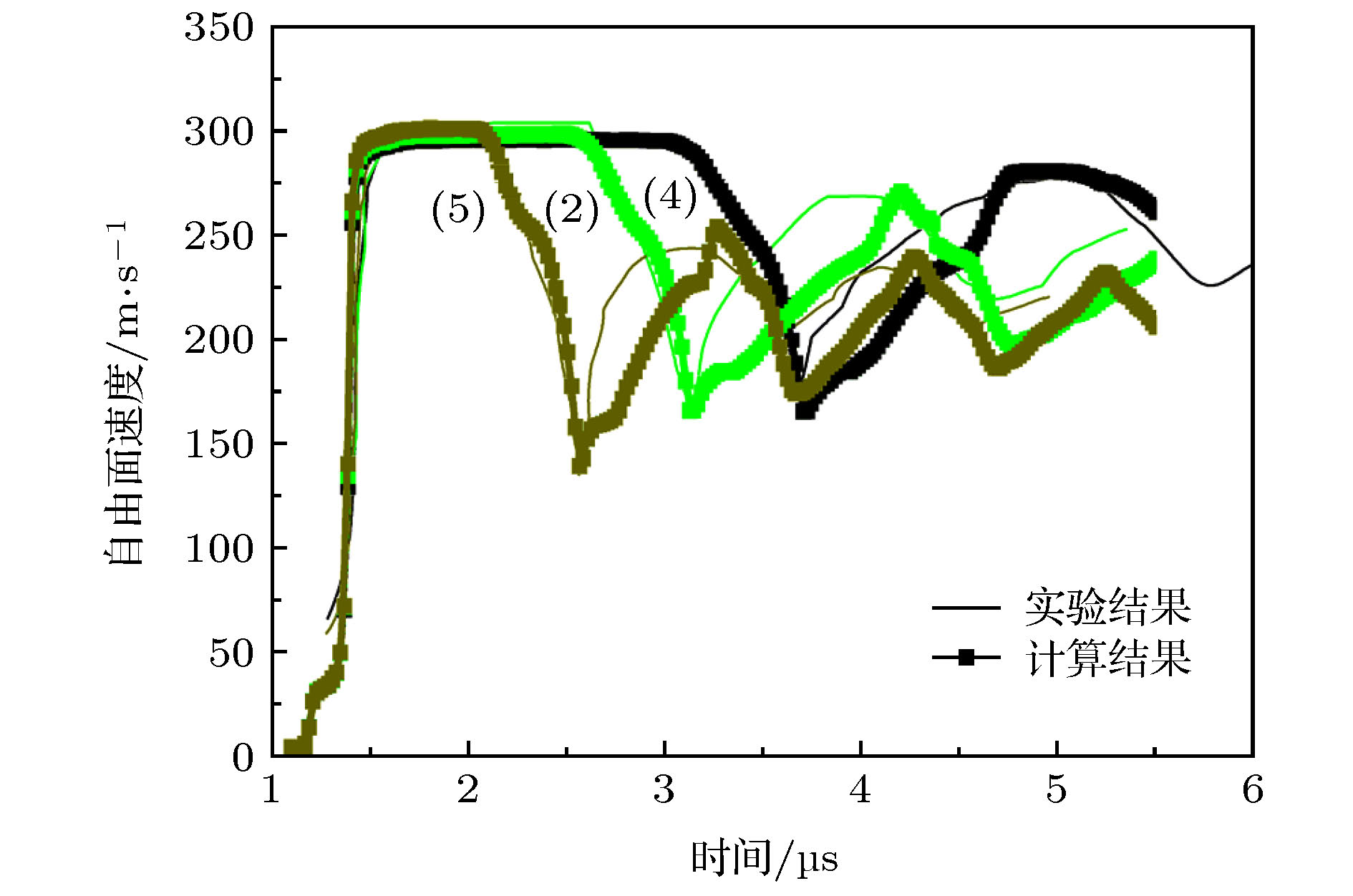
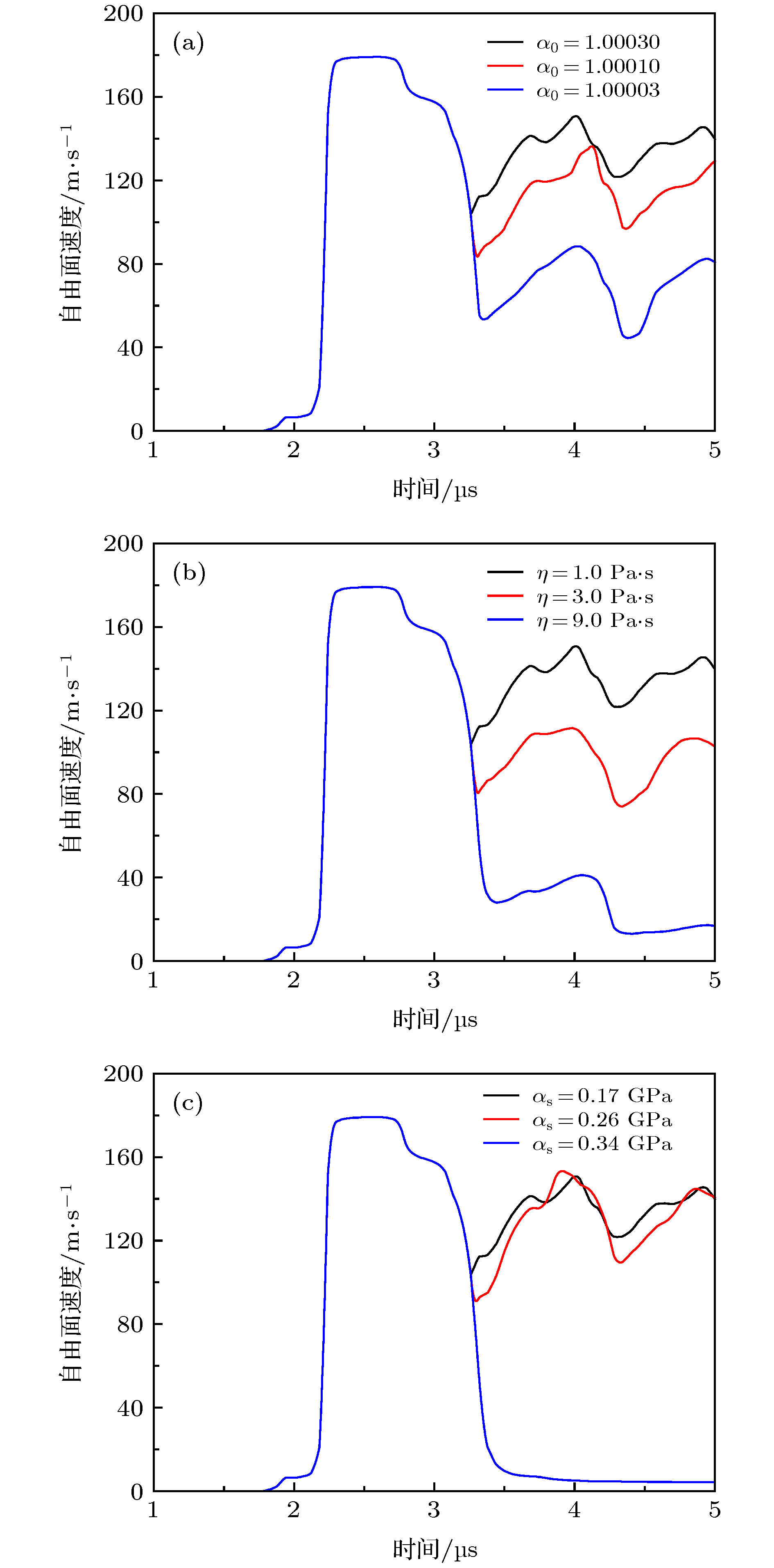
-
Spallation of ductile metal is of great importance in many scientific and engineering fields, which is due to the interaction between the incident shock waves and the reflected waves. Physically, the spallation is caused by nucleation, growth and coalescence of microvoids for ductile material. Therefore, numerical simulation of spall process usually involves theoretical model of void growth. However, due to the limited knowledge of microvoid properties, many empirical parameters are included in the void growth model, which are usually determined by comparing numerical results with experimental data. Therefore, a key problem arises in the numerical modeling of damage and spall fracture, that how the parameters of the void growth damage model can be determined. In this work, we present a theoretical method to determine the parameters based on the free surface velocity (FSV) profile. Firstly, the critical state of damage is discussed based on the relationship between characteristics of FSV and change of physical quantity in spall plane. Then, the propagation and interaction of shock waves during the evolution of spall damage are considered. Lastly, the physical meanings of the parameters of the void growth damage model are further discussed. So, based on the relation among spall strength, damage and pull-back of FSV, a physics-based method to determine the parameters of the model is given. The applicability of this method is verified by the simulation of the spall experimental data on typical ductile metals OFHC copper and tantalum. The parameter-determining method given in this paper can not only expand the scope of application of the damage model and effectively improve the reliability of the calculation results, but also provide a good reference for the determination of parameters of other spall damage model.
-
Keywords:
- ductile metal /
- spall damage /
- void growth damage model /
- determination method of damage model parameters
[1] Meyers M A, Aimone C T 1983 Prog. Mater. Sci. 28 1
Google Scholar
[2] Antoun T, Seaman L, Curran D R, Kanel G I, Razorenov S V, Utkin A V 2003 Spall Fracture (New York: Springer-Verlag
[3] Kanel G I 2010 Int. J. Fract. 163 173
Google Scholar
[4] Tuler FR, Butcher B M 1968 Int. J. Fract. 44 431
[5] Johnson J N 1981 J. Appl. Phys. 52 2812
Google Scholar
[6] Tonks D L, Thissell W R, Schwartz D S 2003 Shock Compression of Condensed Matter (New York: Melville)p507
[7] Czarnota C, Jacques N, Mercier S, Molinari A 2008 J. Mech. Phys. Solids 56 1624
Google Scholar
[8] Wilkerson J W, Ramesh K T 2016 Phys. Rev. Lett. 117 215503
Google Scholar
[9] Zhang F G, Zhou H Q, Hu J, Shao J L, Zhang G C, Hong T, He B 2012 Chin. Phys. B 21 094601
Google Scholar
[10] Bai Y L, Ke F J, Xia M F 1991 Acta Mech. Sin. 7 59
Google Scholar
[11] 裴晓阳, 彭辉, 贺红亮, 李平 2015 64 054601
Google Scholar
Pei X Y, Peng H, He H L, Li P 2015 Acta Phys. Sin. 64 054601
Google Scholar
[12] 张凤国, 周洪强 2013 62 164601
Google Scholar
Zhang F G, Zhou H Q 2013 Acta Phys. Sin. 62 164601
Google Scholar
[13] Wilkerson J W 2017 Int. J. Plast. 95 1
Google Scholar
[14] Jacques N, Mercier S, Molinari A 2012 J. Mech. Phys. Solids 60 665
Google Scholar
[15] Johnson J N, Gray III G T, Bourne N K 1999 J. Appl. Phys. 86 4892
Google Scholar
[16] Escobedo J P, Dennis-Koller D, Cerreta E K, et al. 2011 J. Appl. Phys. 110 033513
Google Scholar
[17] Roy G 2003 Ph. D. Dissertation (ENSMA: University of Poitiers) (In French)
[18] 谢普初, 汪小松, 胡昌明, 胡建波, 张凤国, 王永刚 2020 69 034601
Google Scholar
Xie P C, Wang X S, Hu C M, Hu J B, Zhang F G, Wang Y G 2020 Acta Phys. Sin. 69 034601
Google Scholar
[19] Versino D, Bronkhorst C A 2018 Comput. Meth. Appl. Mech. Eng. 333 395
Google Scholar
[20] Turley W D, Fensin S J, Hixson R S, Jones D R, La Lone B M, Stevens G D, Thomas S A, Veeser L R 2018 J. Appl. Phys. 123 055102
Google Scholar
[21] Rajendran A M, Dietenberger M A, Grove D J 1989 J. Appl. Phys. 65 1521
Google Scholar
[22] 张凤国, 周洪强, 张广财, 洪涛 2011 60 074601
Google Scholar
Zhang F G, Zhou H Q, Zhang G C, Hong T 2011 Acta Phys. Sin. 60 074601
Google Scholar
[23] Romanchenko V I, Stepanov G V 1980 J. Appl. Mech. Tech. Phys. 21 141
Google Scholar
[24] Ikkurthi V R, Chaturvedi S 2012 Int. J. Plast. Conf. Ser. 377 012099
[25] Zerilli F J, Armstrong R W 1987 J. Appl. Phys. 61 1816
Google Scholar
[26] 彭建祥, 李英雷, 李大红 2003 爆炸与冲击 23 183
Google Scholar
Peng J X, Li Y L, Li D H 2003 Explosion and Shock Waves 23 183
Google Scholar
-
图 1 损伤模型参数对自由面速度的影响 (a) 初始孔隙度的影响; (b) 剪切黏性系数的影响; (c) 材料硬化参数的影响
Figure 1. Influences of spall model parameters on free surface velocities: (a) Effects of initial porosity; (b) effects of shear viscosity; (c) effects of work hardening.
图 2 自由面速度曲线典型特征
Figure 2. Characters of free surface velocity profile.
图 3 OFHC铜层裂的自由面速度曲线
Figure 3. Simulated free surface velocity profile for OFHC copper.
图 4 不同飞片撞击速度的自由面速度曲线
Figure 4. Simulated free surface velocity profiles with varied impact velocities.
图 5 不同飞片厚度的自由面速度曲线
Figure 5. Simulated free surface velocity profiles with varied flyer thickness.
表 1 OFHC铜和钽的基本力学参数
Table 1. Material parameters of OFHC copper and tantalum.
密度/kg·m–3 剪切模量/GPa 屈服强度/GPa 体积声速/m·s–1 纵波声速/m·s–1 格林内森系数 OFHC铜 8924 48.4 0.15 3910 4770 2.00 钽 16660 69.0 0.70 3386 4187 1.67 
DownLoad: CSV
表 2 OFHC铜和钽的ZA本构模型参数
Table 2. Material parameters of OFHC copper and tantalum for Zerilli-Armstrong constitutive relations.
A0/GPa A1/GPa A2 A3 A4/GPa n OFHC铜 0.0465 0.890 0.00280 0.00015 0.0185 钽 0.2950 1.519 0.00953 0.00032 0.4070 0.582
DownLoad: CSV
表 3 实验列表
Table 3. Parameters of shock experiments.
实验1 实验2 实验3 实验4 实验5 冲击速度/m·s–1 412 306 212 303 307 飞片厚度/mm 3 3 3 4 2 靶板厚度/mm 4.95 4.95 4.95 4.95 4.95
DownLoad: CSV
-
[1] Meyers M A, Aimone C T 1983 Prog. Mater. Sci. 28 1
Google Scholar
[2] Antoun T, Seaman L, Curran D R, Kanel G I, Razorenov S V, Utkin A V 2003 Spall Fracture (New York: Springer-Verlag
[3] Kanel G I 2010 Int. J. Fract. 163 173
Google Scholar
[4] Tuler FR, Butcher B M 1968 Int. J. Fract. 44 431
[5] Johnson J N 1981 J. Appl. Phys. 52 2812
Google Scholar
[6] Tonks D L, Thissell W R, Schwartz D S 2003 Shock Compression of Condensed Matter (New York: Melville)p507
[7] Czarnota C, Jacques N, Mercier S, Molinari A 2008 J. Mech. Phys. Solids 56 1624
Google Scholar
[8] Wilkerson J W, Ramesh K T 2016 Phys. Rev. Lett. 117 215503
Google Scholar
[9] Zhang F G, Zhou H Q, Hu J, Shao J L, Zhang G C, Hong T, He B 2012 Chin. Phys. B 21 094601
Google Scholar
[10] Bai Y L, Ke F J, Xia M F 1991 Acta Mech. Sin. 7 59
Google Scholar
[11] 裴晓阳, 彭辉, 贺红亮, 李平 2015 64 054601
Google Scholar
Pei X Y, Peng H, He H L, Li P 2015 Acta Phys. Sin. 64 054601
Google Scholar
[12] 张凤国, 周洪强 2013 62 164601
Google Scholar
Zhang F G, Zhou H Q 2013 Acta Phys. Sin. 62 164601
Google Scholar
[13] Wilkerson J W 2017 Int. J. Plast. 95 1
Google Scholar
[14] Jacques N, Mercier S, Molinari A 2012 J. Mech. Phys. Solids 60 665
Google Scholar
[15] Johnson J N, Gray III G T, Bourne N K 1999 J. Appl. Phys. 86 4892
Google Scholar
[16] Escobedo J P, Dennis-Koller D, Cerreta E K, et al. 2011 J. Appl. Phys. 110 033513
Google Scholar
[17] Roy G 2003 Ph. D. Dissertation (ENSMA: University of Poitiers) (In French)
[18] 谢普初, 汪小松, 胡昌明, 胡建波, 张凤国, 王永刚 2020 69 034601
Google Scholar
Xie P C, Wang X S, Hu C M, Hu J B, Zhang F G, Wang Y G 2020 Acta Phys. Sin. 69 034601
Google Scholar
[19] Versino D, Bronkhorst C A 2018 Comput. Meth. Appl. Mech. Eng. 333 395
Google Scholar
[20] Turley W D, Fensin S J, Hixson R S, Jones D R, La Lone B M, Stevens G D, Thomas S A, Veeser L R 2018 J. Appl. Phys. 123 055102
Google Scholar
[21] Rajendran A M, Dietenberger M A, Grove D J 1989 J. Appl. Phys. 65 1521
Google Scholar
[22] 张凤国, 周洪强, 张广财, 洪涛 2011 60 074601
Google Scholar
Zhang F G, Zhou H Q, Zhang G C, Hong T 2011 Acta Phys. Sin. 60 074601
Google Scholar
[23] Romanchenko V I, Stepanov G V 1980 J. Appl. Mech. Tech. Phys. 21 141
Google Scholar
[24] Ikkurthi V R, Chaturvedi S 2012 Int. J. Plast. Conf. Ser. 377 012099
[25] Zerilli F J, Armstrong R W 1987 J. Appl. Phys. 61 1816
Google Scholar
[26] 彭建祥, 李英雷, 李大红 2003 爆炸与冲击 23 183
Google Scholar
Peng J X, Li Y L, Li D H 2003 Explosion and Shock Waves 23 183
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 5056
- PDF Downloads: 85
- Cited By: 0
