-
In this paper, we study the generation mechanism of bright and dark solitary waves and rogue wave for the fourth-order dispersive nonlinear Schrödinger (FODNLS) equation, which can not only model the nonlinear propagation and interaction of ultrashort pulses in the high-speed optical fiber transmission system, but also govern the nonlinear spin excitations in the onedimensional isotropic biquadratic Heisenberg ferromagnetic spin with the octupole-dipole interaction. Firstly, via the phase plane analysis, we obtain both the homoclinic and heteroclinic orbits for the two-dimensional plane autonomous system reduced from the FODNLS equation. Further, we derive the bright and dark solitary wave solutions under the corresponding conditions, which reveals the relationship between the homoclinic (heteroclinic) orbit and solitary wave. Secondly, based on the exact first-order breather solution of the FODNLS equation over a nonvanishing background, we give the explicit expressions of group and phase velocities, and reveal that there exists a jump in both the velocities. Finally, in order to verify that the breather becomes a rogue wave at the jumping point, we obtain the first-order rogue wave solution by taking the limit of the breather solution at such point, which confirms the relationship of the generation of rogue wave with the velocity discontinuity.
[1] He J S, Xu S W, Porsezian 2012 Phys. Rev. E 86 066603
Google Scholar
[2] Bludov Y V, Konotop V V, Akhmediev N 2009 Phys. Rev. A 80 033610
Google Scholar
[3] Stenflo L, Marklund M 2010 J. Plasma Phys. 76 293
Google Scholar
[4] Li M, Shui J J, Xu T 2018 Appl. Math. Lett. 83 110
Google Scholar
[5] Li M, Shui J J, Huang Y H, Wang L, Li H J 2018 Phys. Scr. 93 115203
Google Scholar
[6] Li M, Xu T, Meng D X 2016 J. Phys. Soc. Jpn. 85 124001
Google Scholar
[7] Xu T, Lan S, Li M, Li L L, Zhang G W 2019 Physica D 390 47
Google Scholar
[8] Xu T, Pelinovsky D E 2019 Phys. Lett. A 383 125948 ; Xu T, Chen Y, Li M, Meng D X 2019 Chaos 29 123124
[9] Agrawal G P 2012 Nonlinear Fiber Optics (5th ed.) (San Diego: Academic Press) pp120–150
[10] Ma Y C 1979 Stud. Appl. Math. 60 43
Google Scholar
[11] Akhmediev N N, Korneev V I 1986 Theor. Math. Phys. 69 1089
Google Scholar
[12] Calini A, Schober C M 2002 Phys. Lett. A 298 335
Google Scholar
[13] Wang L, Zhang J H, Wang Z Q, Liu C, Li M, Qi F H, Guo R 2016 Phys. Rev. E 93 012214
Google Scholar
[14] Akhmediev N N, Soto-Crespo J M, Ankiewica A 2009 Phys. Lett. A 373 2137
Google Scholar
[15] Zuo D W, Gao Y T, Xue L, Feng Y J 2014 Chaos, Solitons Fractals 69 217227
[16] Solli D R, Ropers C, Koonath P, Jalali B 2007 Nature 450 1054
Google Scholar
[17] Chabchoub A, Hoffmann N P, Akhmediev N 2011 Phys. Rev. E 106 204502
[18] Peregrine D H 1983 J. Austral. Math. Soc. Ser. B 25 16
Google Scholar
[19] Akhmediev N N, Soto-Crespo J M, Ankiewica A 2009 Phys. Rev. A 80 043818
Google Scholar
[20] Benjamin T B, Feir J E 1967 J. Fluid. Mech. 27 417
Google Scholar
[21] Toffoli T, Fernandez L, Monbaliu J, Benoit M, Gagnaire-Renou E, Lefèvre J M, Cavaleri L, Proment D, Pakozdi C, Stansberg C T, Waseda T, Onorato M 2013 Phys. Fluids 25 091701
Google Scholar
[22] Mussot A, Kudlinski A, Kolobov M, Louvergneaux E, Douay M, Taki M 2009 Opt. Express 17 17010
Google Scholar
[23] Genty G, de Sterke C M, Bang O, Dias F, Akhmediev N, Dudley J M 2010 Phys. Lett. A 374 989
Google Scholar
[24] He J S, Xu S W, Porsezian K, Cheng Y, Dinda P T 2016 Phys. Rev. E 93 062201
Google Scholar
[25] He J S, Xu S W, Porsezian K, Dinda P T, Mihalache D, Malomed B A, Ding E 2017 Rom. J. Phys. 62 203
[26] Liu S D, Liu S K 1994 Soliton Wave and Turbulence (Chinese version) (1st ed.) (Shanghai: Shanghai Scientific and Technological Education Press) pp90–97
[27] Infeld E, Rowlands G 2000 Nonlinear Waves, Solitons and Chaos (2th ed.) (Cambridge: Cambridge University Press) pp144–156
[28] Choudhuri A, Porsezian K 2013 Phys. Rev. A 88 033808
Google Scholar
[29] Porsezian K, Daniel M, Lakshmanan M 1992 J. Math. Phys. 33 1807
Google Scholar
[30] Wang L H, Porsezian K, He J S 2013 Phys. Rev. E 87 053202
Google Scholar
[31] Azzouzi F, Triki H, Mezghiche K, Akrmi A E 2009 Chaos, Solitons Fractals 39 1304
Google Scholar
[32] Daniel M, Latha M M 2001 Physica A 298 351
Google Scholar
[33] Zhang H Q, Tian B, Meng X H, Lü X, Liu W J 2009 Eur. Phys. J. B 72 233
Google Scholar
[34] Liu R X, Tian B, Liu L C, Qin B, Lü X 2013 Physica B 413 120
Google Scholar
[35] Peregrine D H 1983 The ANZIAM Journal 25 16
[36] Chen S H, Mihalache D 2015 J. Phys.A: Math. Theor. 48 215202
Google Scholar
[37] Liu B Y, Fokas A S, Mihalache D, He J S 2016 Rom. Rep. Phys. 68 1425
[38] Zakharov V E, Gelash A A 2013 Phys. Rev. Lett. 111 054101
Google Scholar
[39] Whitham G B 1999 Linear and Nonlinear Waves (2nd ed.) (New York: A Wiley-Interscience Publication) pp363-374
[40] Ruban V, Kodama Y, Ruderman M, et al. 2010 Eur. Phys. J. Special Topics 185 5
Google Scholar
-
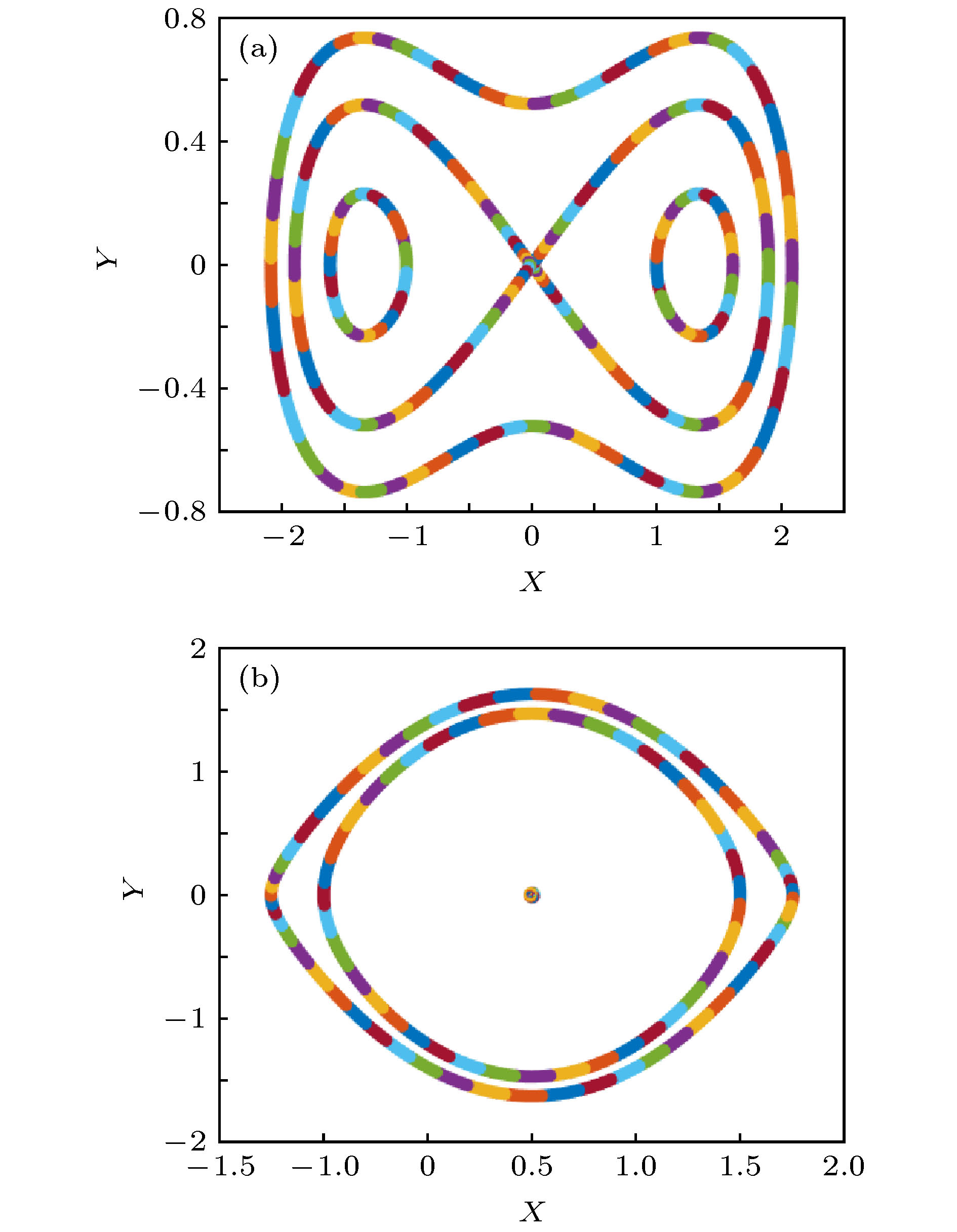
图 2 (a)由明孤立波解(22)式描述的明孤立波传输图形, 其中参数选取为 α1 = 1, α2 = 2, α3 = 1, α4 = 8, α5 = 2,α6 = 6, α7 = 4, α8 = 6, c = 1, K = 1,
$\varOmega $ = 51/16, ε = 1, a = 1; (b) 由暗孤立波解(25)式描述的暗孤立波传输图形, 其中参数选取为α1 = –1, α2 = 2, α3 = 1, α4 = –8, α5 = –2, α6 = –6, α 7 = –4, α8 = 6, c = –7, K = 1,$\varOmega $ = –123/32, ε = 1, a = 1Figure 2. (a) Propagation of bright solitary wave via Solution (22) with the parameters chosen as α1 = 1, α2 = 2, α3 = 1, α4 = 8, α5 = 2, α6 = 6, α7 = 4, α8 = 6, c = 1, K = 1,
$\varOmega $ = 51/16, ε = 1, a = 1; (b) propagation of dark solitary wave via Solution (25) with the parameters chosen as α1 = –1, α2 = 2, α3 = 1, α4 = –8, α5 = –2, α6 = –6, α7 = –4, α8 = 6, c = –7, K = 1,$\varOmega $ = –123/32, ε = 1, a = 1.
图 4 呼吸子的群速度
$V_{\rm g}$ (红实线)和相速度$V_{\rm p}$ (蓝虚线)随参数a的变化关系Figure 4. Group velocity
$V_{\rm g}$ (red-solid line) and phase velocity$V_{\rm p}$ (blue-dot line) of the breather
图 6 (a) 群速度
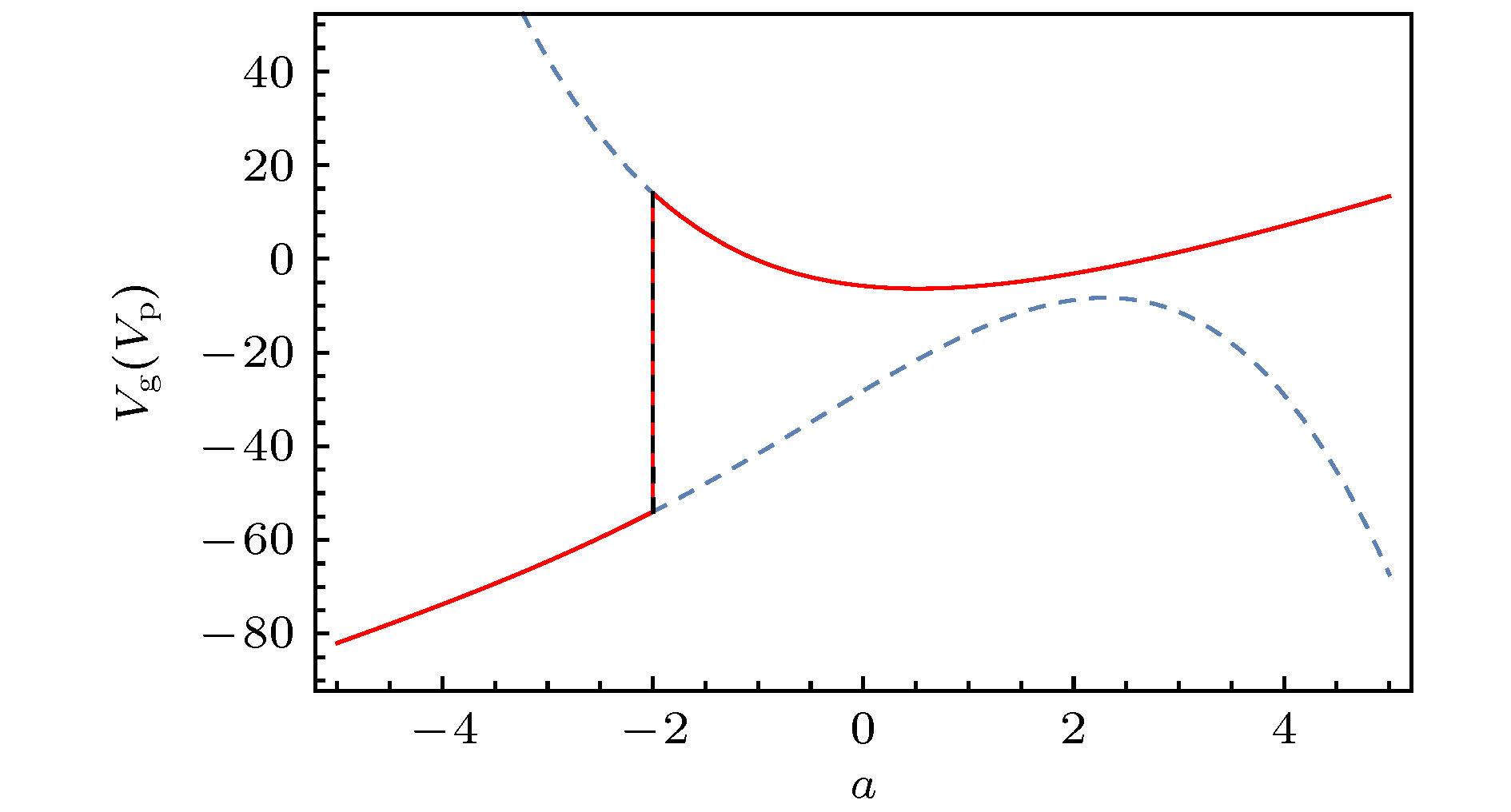
$V_{\rm g}$ 随振幅参数c的变化(红实线)和(b)相速度$V_{\rm p}$ 随振幅参数c的变化(蓝点线), 其中参数选取为$\xi={1}/{2}(\sqrt{-4 c^2}-a)$ ,$\eta=0$ 和$a=1$ Figure 6. Variation of the group velocity
$V_{\rm g}$ (red-solid line) and phase velocity$V_{\rm p}$ (blue-dot line) about the amplitude parameter c with the parameters chosen as$\xi={1}/{2}(\sqrt{-4 c^2}-a)$ ,$\eta=0$ and$a=1$ . -
[1] He J S, Xu S W, Porsezian 2012 Phys. Rev. E 86 066603
Google Scholar
[2] Bludov Y V, Konotop V V, Akhmediev N 2009 Phys. Rev. A 80 033610
Google Scholar
[3] Stenflo L, Marklund M 2010 J. Plasma Phys. 76 293
Google Scholar
[4] Li M, Shui J J, Xu T 2018 Appl. Math. Lett. 83 110
Google Scholar
[5] Li M, Shui J J, Huang Y H, Wang L, Li H J 2018 Phys. Scr. 93 115203
Google Scholar
[6] Li M, Xu T, Meng D X 2016 J. Phys. Soc. Jpn. 85 124001
Google Scholar
[7] Xu T, Lan S, Li M, Li L L, Zhang G W 2019 Physica D 390 47
Google Scholar
[8] Xu T, Pelinovsky D E 2019 Phys. Lett. A 383 125948 ; Xu T, Chen Y, Li M, Meng D X 2019 Chaos 29 123124
[9] Agrawal G P 2012 Nonlinear Fiber Optics (5th ed.) (San Diego: Academic Press) pp120–150
[10] Ma Y C 1979 Stud. Appl. Math. 60 43
Google Scholar
[11] Akhmediev N N, Korneev V I 1986 Theor. Math. Phys. 69 1089
Google Scholar
[12] Calini A, Schober C M 2002 Phys. Lett. A 298 335
Google Scholar
[13] Wang L, Zhang J H, Wang Z Q, Liu C, Li M, Qi F H, Guo R 2016 Phys. Rev. E 93 012214
Google Scholar
[14] Akhmediev N N, Soto-Crespo J M, Ankiewica A 2009 Phys. Lett. A 373 2137
Google Scholar
[15] Zuo D W, Gao Y T, Xue L, Feng Y J 2014 Chaos, Solitons Fractals 69 217227
[16] Solli D R, Ropers C, Koonath P, Jalali B 2007 Nature 450 1054
Google Scholar
[17] Chabchoub A, Hoffmann N P, Akhmediev N 2011 Phys. Rev. E 106 204502
[18] Peregrine D H 1983 J. Austral. Math. Soc. Ser. B 25 16
Google Scholar
[19] Akhmediev N N, Soto-Crespo J M, Ankiewica A 2009 Phys. Rev. A 80 043818
Google Scholar
[20] Benjamin T B, Feir J E 1967 J. Fluid. Mech. 27 417
Google Scholar
[21] Toffoli T, Fernandez L, Monbaliu J, Benoit M, Gagnaire-Renou E, Lefèvre J M, Cavaleri L, Proment D, Pakozdi C, Stansberg C T, Waseda T, Onorato M 2013 Phys. Fluids 25 091701
Google Scholar
[22] Mussot A, Kudlinski A, Kolobov M, Louvergneaux E, Douay M, Taki M 2009 Opt. Express 17 17010
Google Scholar
[23] Genty G, de Sterke C M, Bang O, Dias F, Akhmediev N, Dudley J M 2010 Phys. Lett. A 374 989
Google Scholar
[24] He J S, Xu S W, Porsezian K, Cheng Y, Dinda P T 2016 Phys. Rev. E 93 062201
Google Scholar
[25] He J S, Xu S W, Porsezian K, Dinda P T, Mihalache D, Malomed B A, Ding E 2017 Rom. J. Phys. 62 203
[26] Liu S D, Liu S K 1994 Soliton Wave and Turbulence (Chinese version) (1st ed.) (Shanghai: Shanghai Scientific and Technological Education Press) pp90–97
[27] Infeld E, Rowlands G 2000 Nonlinear Waves, Solitons and Chaos (2th ed.) (Cambridge: Cambridge University Press) pp144–156
[28] Choudhuri A, Porsezian K 2013 Phys. Rev. A 88 033808
Google Scholar
[29] Porsezian K, Daniel M, Lakshmanan M 1992 J. Math. Phys. 33 1807
Google Scholar
[30] Wang L H, Porsezian K, He J S 2013 Phys. Rev. E 87 053202
Google Scholar
[31] Azzouzi F, Triki H, Mezghiche K, Akrmi A E 2009 Chaos, Solitons Fractals 39 1304
Google Scholar
[32] Daniel M, Latha M M 2001 Physica A 298 351
Google Scholar
[33] Zhang H Q, Tian B, Meng X H, Lü X, Liu W J 2009 Eur. Phys. J. B 72 233
Google Scholar
[34] Liu R X, Tian B, Liu L C, Qin B, Lü X 2013 Physica B 413 120
Google Scholar
[35] Peregrine D H 1983 The ANZIAM Journal 25 16
[36] Chen S H, Mihalache D 2015 J. Phys.A: Math. Theor. 48 215202
Google Scholar
[37] Liu B Y, Fokas A S, Mihalache D, He J S 2016 Rom. Rep. Phys. 68 1425
[38] Zakharov V E, Gelash A A 2013 Phys. Rev. Lett. 111 054101
Google Scholar
[39] Whitham G B 1999 Linear and Nonlinear Waves (2nd ed.) (New York: A Wiley-Interscience Publication) pp363-374
[40] Ruban V, Kodama Y, Ruderman M, et al. 2010 Eur. Phys. J. Special Topics 185 5
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 13050
- PDF Downloads: 263
- Cited By: 0
