Topology optimization of the volume-to-point heat conduction problem at micro- and nano-scale

Li Han-Ling; Cao Bing-Yang

doi:10.7498/aps.68.20190923

Abstract

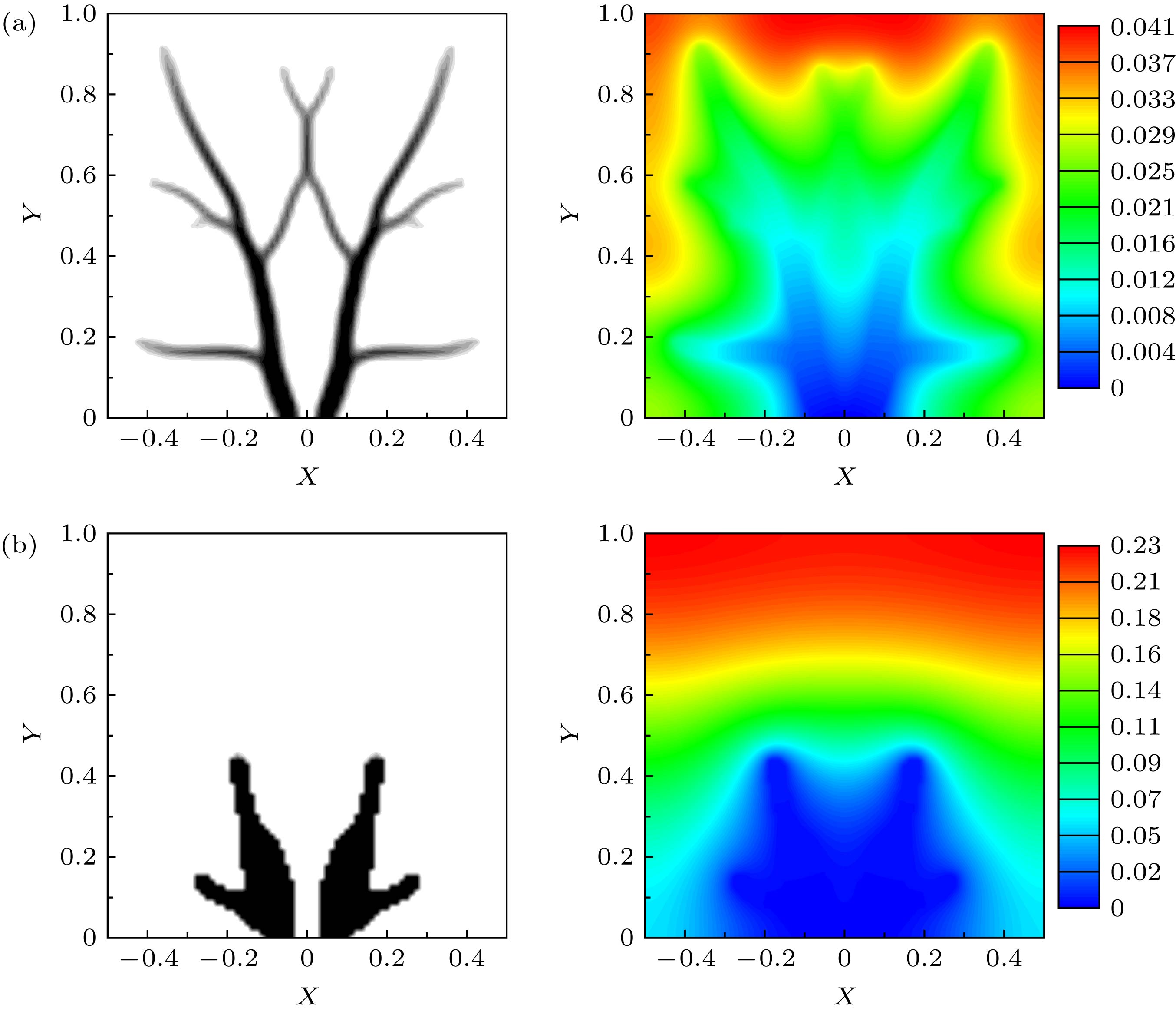
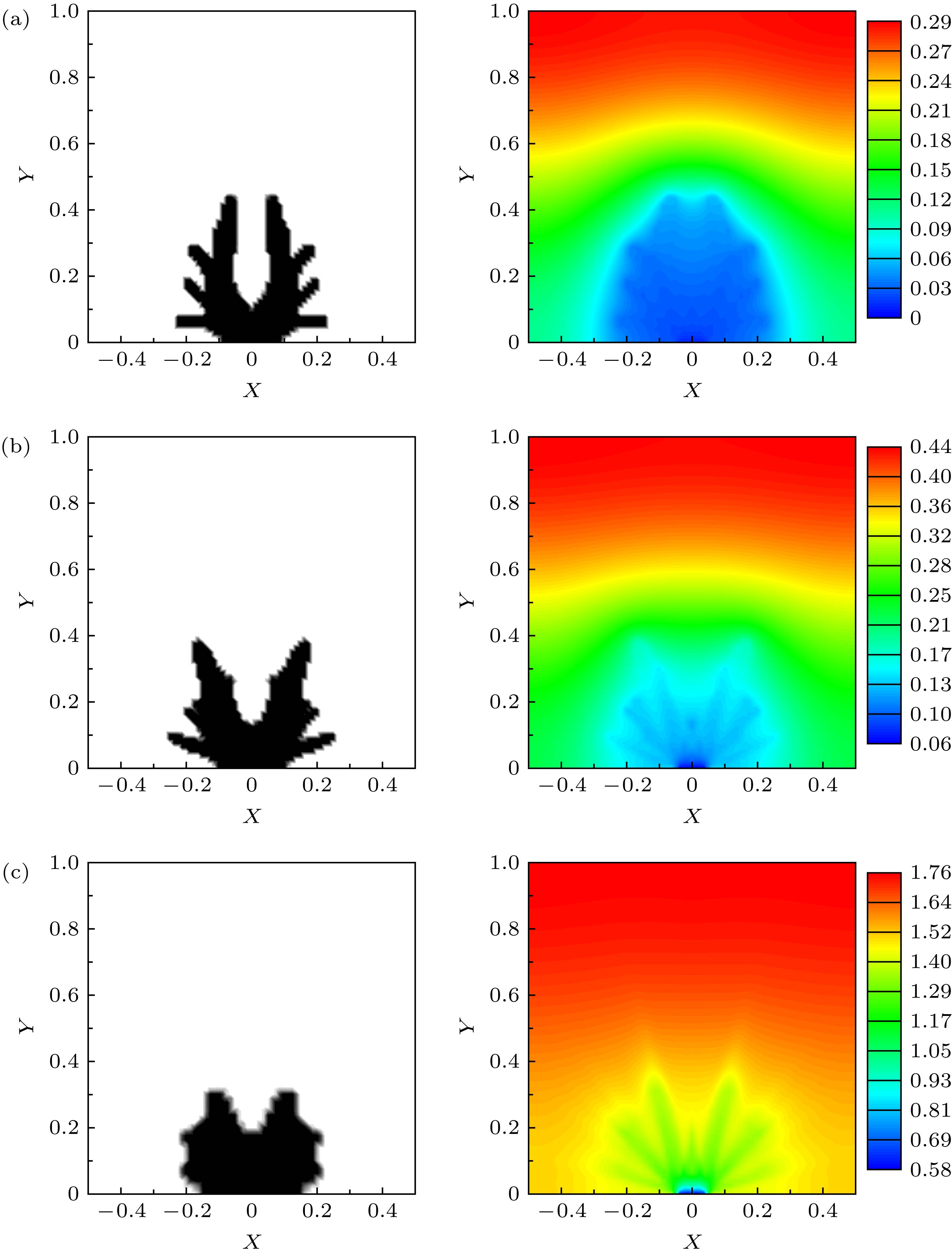
The volume-to-point (VP) heat conduction problem is one of the fundamental problems of cooling for electronic devices. The existed reports about the VP problem are mainly based on the Fourier’s law which works well at the macroscopic scale. However, the length scale of modern electronic devices has reduced to micro- and nano-scale, at which optimization methods that are capable of dealing with the non-Fourier heat conduction are desired now. In this paper, phonon Boltzmann transport equation (BTE) and solid isotropic material with penalization (SIMP) method are coupled to develop a topology optimization method for ballistic-diffusive heat conduction. Phonon BTE is transformed into equation of phonon radiative transport, which is solved by the discrete ordinate method. To realize the topology optimization, SIMP method is adopted to penalize the phonon extinction coefficient, which equals to the reciprocal of phonon mean-free-path, and an explicit constraint on the global gradient of the nominal material density is used to ensure the solutions being well-posed and mesh-independent. By using the developed topology optimization method, it is found that the optimal material distributions for the VP problem in ballistic-diffusive heat conduction significantly deviate from the traditional tree-like structure obtained in diffusive heat conduction, and the results vary with the Knudsen number (Kn). This is related to the different coefficient interpolation ways in the SIMP method and phonon ballistic transport. When Kn → 0, instead of converging to the conventional tree-like structure which fully stretches into the interior zone, the new method gradually produces the result obtained by the topology optimization which interpolates the reciprocal of the thermal conductivity in diffusive heat conduction. As Kn increases, the high thermal-conductive filling materials show a trend to gather around the low-temperature boundary, and there are more thick and strong trunk structures, less tiny and thin branch structures in the optimized material distributions. In addition, the ratio of the optimized average temperature to the value of the uniform material distribution $\left( {T_{{\rm{ave}},{\rm{opt}}}^{\rm{*}}/T_{{\rm{ave}},{\rm{uni}}}^{\rm{*}}} \right)$ also increases. The dependence of the topology optimization results on Kn can be attributed to the size effect of the thermal conductivity caused by phonon ballistic transport. In the diffusive heat conduction, filling materials with different length scales have the same efficiency to build high thermal-conductive channels. However, with ballistic effect enhancing, size effect makes the effective thermal conductivities of the branch structure lower than those of the trunk structure, as the former is smaller than the latter. As a result, the branch structures are less efficient compared with the trunk structures in terms of building high thermal-conductive channels, and the optimal material distributions have more trunk structures and fewer branch structures. When the ballistic effect becomes significant enough, say at Kn = 0.1, the topology optimization gets a dough-like material distribution in which branches merge into trunks. The proposed topology optimization method have the potential to provide guidance in designing nanoscale electronic devices for improving the heat dissipation capability.

Keywords:

volume-to-point heat conduction problem /
topology optimization /
micro- and nano-scale /
phonon Boltzmann transport equation

Authors and contacts

Key Laboratory for Thermal Science and Power Engineering of Ministry of Education, Department of Engineering Mechanics, Tsinghua University, Beijing 100084, China

Corresponding author: Cao Bing-Yang, caoby@tsinghua.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 51825601, 51676108, 51621062).

FullText HTML : translate this paragraph

References

[1]	Bagnall K R, Wang E N 2018 IEEE Trans. Comp. Pack. Man. 8 606
[2]	Ahmed H E, Salman B H, Kherbeet A S, Ahmed M I 2018 Int. J. Heat Mass Transf. 118 129 Google Scholar
[3]	Narendran N, Gu Y, Freyssinier J P, Yu H, Deng L 2004 J. Cryst. Growth 268 449 Google Scholar
[4]	Pop E 2010 Nano Res. 3 147 Google Scholar
[5]	Garimella S V, Persoons T, Weibel J A, Gektin V 2017 IEEE Trans. Comp. Pack. Man. 7 1191
[6]	Hua Y C, Li H L, Cao B Y 2019 IEEE Trans. Electron Dev. 66 3296
[7]	Yang M, Cao B Y 2019 Appl. Therm. Eng. 159 113896 Google Scholar
[8]	Bejan A 1997 Int. J. Heat Mass Transf. 40 799 Google Scholar
[9]	Cheng X G, Li Z X, Guo Z Y 2003 Sci. China: Technol. Sci. 46 296
[10]	Gersborg-Hansen A, Bendsøe M P, Sigmund O 2006 Struct. Multidiscip. O. 31 251 Google Scholar
[11]	Zhang Y C, Liu S T 2008 Heat Mass Transf. 44 1217 Google Scholar
[12]	Dirker J, Meyer J P 2013 J. Heat Transf. 135 111010 Google Scholar
[13]	Dbouk T 2017 Appl. Therm. Eng. 112 841 Google Scholar
[14]	Xu X H, Liang X G, Ren J X 2007 Int. J. Heat Mass Transf. 50 1675 Google Scholar
[15]	Sigmund O, Maute K 2013 Struct. Multidiscip. O. 48 1031 Google Scholar
[16]	Cahill D G, Braun P V, Chen G, Clarke D R, Fan S, Goodson K E, Keblinski P, King W P, Mahan G D, Majumdar A 2014 Appl. Phys. Rev. 1 11305 Google Scholar
[17]	Volz S, Shiomi J, Nomura M, Miyazaki K 2016 J. Therm. Sci. Tech.-Jpn 11 T1 Google Scholar
[18]	Bao H, Chen J, Gu X K, Cao B Y 2018 ES Energy Environ. 1 16
[19]	Xie G F, Ju Z F, Zhou K K, Wei X L, Guo Z X, Cai Y Q, Zhang G 2018 npj Comput. Mater. 4 21 Google Scholar
[20]	Guo Z Y 2018 ES Energy Environ. 1 4
[21]	Lu Z X, Ruan X L 2019 ES Energy Environ. 4 5
[22]	Yao W J, Cao B Y 2016 Phys. Lett. A 380 2105 Google Scholar
[23]	Ziman J M 2001 Electrons and Phonons: the Theory of Transport Phenomena in Solids (Oxford: Clarendon Press) pp1–51
[24]	Chen G 2001 Phys. Rev. Lett. 86 2297 Google Scholar
[25]	Hua Y C, Cao B Y 2014 Int. J. Heat Mass Transf. 78 755 Google Scholar
[26]	Hua Y C, Cao B Y 2016 Int. J. Therm. Sci. 101 126 Google Scholar
[27]	Li H L, Cao B Y 2019 Nanoscale Microscale Thermophys. Eng. 23 10 Google Scholar
[28]	Li B W, Wang J 2003 Phys. Rev. Lett. 91 44301 Google Scholar
[29]	Schleeh J, Mateos J, Íñiguez-de-la-Torre I, Wadefalk N, Nilsson P A, Grahn J, Minnich A J 2014 Nat. Mater. 14 187
[30]	Hua Y C, Cao B Y 2017 Nanoscale Microscale Thermophys. Eng. 3 159
[31]	Li H L, Hua Y C, Cao B Y 2018 Int. J. Heat Mass Transf. 127 1014
[32]	Luckyanova M N, Garg J, Esfarjani K, Jandl A, Bulsara M T, Schmidt A J, Minnich A J, Chen S, Dresselhaus M S, Ren Z 2012 Science 338 936 Google Scholar
[33]	Chen X K, Xie Z X, Zhou W X, Tang L M, Chen K Q 2016 Appl. Phys. Lett. 109 23101 Google Scholar
[34]	Chen X K, Liu J, Peng Z H, Du D, Chen K Q 2017 Appl. Phys. Lett. 110 91907 Google Scholar
[35]	Xie G F, Ding D, Zhang G 2018 Adv. Phys. X 3 1480417
[36]	Kazan M, Guisbiers G, Pereira S, Correia M R, Masri P, Bruyant A, Volz S, Royer P 2010 J. Appl. Phys. 107 83503 Google Scholar
[37]	Ju Y S, Goodson K E 1999 Appl. Phys. Lett. 74 3005 Google Scholar
[38]	Evgrafov A, Maute K, Yang R G, Dunn M L 2009 Int. J. Numer. Meth. Eng. 77 285 Google Scholar
[39]	Murthy J Y, Mathur S R 2002 J. Heat Transf. 124 1176 Google Scholar
[40]	Narumanchi S V, Murthy J Y, Amon C H 2003 J. Heat Transf. 125 896 Google Scholar
[41]	Hamian S, Yamada T, Faghri M, Park K 2015 Int. J. Heat Mass Transf. 80 781 Google Scholar
[42]	Majumdar A 1993 J. Heat Transf. 115 7 Google Scholar
[43]	Chen G 1998 Phys. Rev. B 57 14958 Google Scholar
[44]	Sobolev S L 2018 Phys. Rev. E 97 22122 Google Scholar
[45]	华钰超, 董源, 曹炳阳 2013 62 244401 Google Scholar Hua Y C, Dong Y, Cao B Y 2013 Acta Phys. Sin. 62 244401 Google Scholar
[46]	Hua Y C, Cao B Y 2016 Int. J. Heat Mass Transf. 92 995 Google Scholar
[47]	Peterson R B 1994 J. Heat Transf. 116 815 Google Scholar
[48]	杜建镔 2015 结构优化及其在振动和声学设计中的应用 (北京: 清华大学出版社) 第115页 Du J B 2015 Structural Optimization and Its Applications in Vibration and Acoustic Designs (Beijing: Tsinghua University Press) p115 (in Chinese)
[49]	Bendsøe M P 1989 Struct. Optimization 1 193 Google Scholar
[50]	Sigmund O, Petersson J 1998 Struct. Optimization 16 68 Google Scholar
[51]	Zhang Y C, Liu S T 2008 Prog. Nat. Sci. 18 665 Google Scholar
[52]	Petersson J, Sigmund O 1998 Int. J. Numer. Meth. Eng. 41 1417 Google Scholar
[53]	Bendsoe M P, Sigmund O 2004 Topology Optimization: Theory, Methods, and Applications (Berlin: Springer) p17
[54]	Svanberg K 1987 Int. J. Numer. Meth. Eng. 24 359 Google Scholar
[55]	Hua Y C, Cao B Y 2018 J. Appl. Phys. 123 114304 Google Scholar
[56]	Alaili K, Ordonez-Miranda J, Ezzahri Y 2018 Int. J. Therm. Sci. 131 40 Google Scholar

Cited By

图 1 体点导热问题示意图

Figure 1. The schematic diagram of the VP problem.

DownLoad: Full-Size Img PowerPoint

图 2 体点导热拓扑优化的流程图

Figure 2. The flow chart of topology optimization for the VP problem.

DownLoad: Full-Size Img PowerPoint

图 3 扩散导热下不同插值方式对材料分布和温度分布的影响　(a)插值k; (b)插值${k^{ - 1}}$

Figure 3. The effect of interpolation ways on the material distributions and temperature distributions in diffusive heat conduction: (a) Interpolating k; (b) interpolating ${k^{ - 1}}$.

DownLoad: Full-Size Img PowerPoint

图 4 扩散导热下拓扑优化得到的材料分布随$\alpha $和n的变化

Figure 4. The material distributions obtained by topology optimization in diffusive heat conduction varying with $\alpha $ and n.

DownLoad: Full-Size Img PowerPoint

图 5 弹道-扩散导热下拓扑优化的材料分布和温度云图随$Kn$的变化　(a) Kn = 0.002; (b) Kn = 0.01; (c) Kn = 0.1

Figure 5. The topology optimization obtained material distributions and temperature distributions varying with Kn in ballistic-diffusive heat conduction: (a) Kn = 0.002; (b) Kn = 0.01; (c) Kn = 0.1.

DownLoad: Full-Size Img PowerPoint

图 6 扩散导热下插值${k^{ - 1}}$的拓扑优化所得的材料分布在$Kn = 0.1$时的温度分布

Figure 6. The temperature distribution for the material distribution obtained by topology optimization which interpolates ${k^{ - 1}}$ in diffusive heat conduction at $Kn = 0.1$.

DownLoad: Full-Size Img PowerPoint

表 1 不同材料分布在不同努森数下对应的无量纲温度平均值

Table 1. The average dimensionless temperature of different material distributions at different Knudsen numbers.

Kn	$T_{{\rm{ave}}}^$(括号内数据为$T_{{\rm{ave}}}^/T_{{\rm{ave}},{\rm{uni}}}^*$)
Kn	均匀分布	分布1	分布2	分布3	分布4	分布5
0.002	0.98(100.0%)	0.33 (33.7%)	0.21 (21.4%)	0.11 (11.2%)	0.12 (12.2%)	0.21 (21.4%)
0.01	1.07(100.0%)	0.57 (53.2%)	0.41(38.3%)	0.30 (28.0%)	0.29 (27.1%)	0.33 (30.8%)
0.1	2.29(100.0%)	1.97 (86.0%)	1.84 (80.3%)	1.64 (71.6%)	1.62 (70.7%)	1.60 (69.9%)
注: 分布1和2分别是扩散导热条件下插值k的拓扑优化结果、插值${k^{ - 1}}$的拓扑优化结果, 分布3—5分别是弹道-扩散导热条件下$Kn$为0.002, 0.01, 0.1时的拓扑优化结果.

DownLoad: CSV

map

[1]	Bagnall K R, Wang E N 2018 IEEE Trans. Comp. Pack. Man. 8 606
[2]	Ahmed H E, Salman B H, Kherbeet A S, Ahmed M I 2018 Int. J. Heat Mass Transf. 118 129 Google Scholar
[3]	Narendran N, Gu Y, Freyssinier J P, Yu H, Deng L 2004 J. Cryst. Growth 268 449 Google Scholar
[4]	Pop E 2010 Nano Res. 3 147 Google Scholar
[5]	Garimella S V, Persoons T, Weibel J A, Gektin V 2017 IEEE Trans. Comp. Pack. Man. 7 1191
[6]	Hua Y C, Li H L, Cao B Y 2019 IEEE Trans. Electron Dev. 66 3296
[7]	Yang M, Cao B Y 2019 Appl. Therm. Eng. 159 113896 Google Scholar
[8]	Bejan A 1997 Int. J. Heat Mass Transf. 40 799 Google Scholar
[9]	Cheng X G, Li Z X, Guo Z Y 2003 Sci. China: Technol. Sci. 46 296
[10]	Gersborg-Hansen A, Bendsøe M P, Sigmund O 2006 Struct. Multidiscip. O. 31 251 Google Scholar
[11]	Zhang Y C, Liu S T 2008 Heat Mass Transf. 44 1217 Google Scholar
[12]	Dirker J, Meyer J P 2013 J. Heat Transf. 135 111010 Google Scholar
[13]	Dbouk T 2017 Appl. Therm. Eng. 112 841 Google Scholar
[14]	Xu X H, Liang X G, Ren J X 2007 Int. J. Heat Mass Transf. 50 1675 Google Scholar
[15]	Sigmund O, Maute K 2013 Struct. Multidiscip. O. 48 1031 Google Scholar
[16]	Cahill D G, Braun P V, Chen G, Clarke D R, Fan S, Goodson K E, Keblinski P, King W P, Mahan G D, Majumdar A 2014 Appl. Phys. Rev. 1 11305 Google Scholar
[17]	Volz S, Shiomi J, Nomura M, Miyazaki K 2016 J. Therm. Sci. Tech.-Jpn 11 T1 Google Scholar
[18]	Bao H, Chen J, Gu X K, Cao B Y 2018 ES Energy Environ. 1 16
[19]	Xie G F, Ju Z F, Zhou K K, Wei X L, Guo Z X, Cai Y Q, Zhang G 2018 npj Comput. Mater. 4 21 Google Scholar
[20]	Guo Z Y 2018 ES Energy Environ. 1 4
[21]	Lu Z X, Ruan X L 2019 ES Energy Environ. 4 5
[22]	Yao W J, Cao B Y 2016 Phys. Lett. A 380 2105 Google Scholar
[23]	Ziman J M 2001 Electrons and Phonons: the Theory of Transport Phenomena in Solids (Oxford: Clarendon Press) pp1–51
[24]	Chen G 2001 Phys. Rev. Lett. 86 2297 Google Scholar
[25]	Hua Y C, Cao B Y 2014 Int. J. Heat Mass Transf. 78 755 Google Scholar
[26]	Hua Y C, Cao B Y 2016 Int. J. Therm. Sci. 101 126 Google Scholar
[27]	Li H L, Cao B Y 2019 Nanoscale Microscale Thermophys. Eng. 23 10 Google Scholar
[28]	Li B W, Wang J 2003 Phys. Rev. Lett. 91 44301 Google Scholar
[29]	Schleeh J, Mateos J, Íñiguez-de-la-Torre I, Wadefalk N, Nilsson P A, Grahn J, Minnich A J 2014 Nat. Mater. 14 187
[30]	Hua Y C, Cao B Y 2017 Nanoscale Microscale Thermophys. Eng. 3 159
[31]	Li H L, Hua Y C, Cao B Y 2018 Int. J. Heat Mass Transf. 127 1014
[32]	Luckyanova M N, Garg J, Esfarjani K, Jandl A, Bulsara M T, Schmidt A J, Minnich A J, Chen S, Dresselhaus M S, Ren Z 2012 Science 338 936 Google Scholar
[33]	Chen X K, Xie Z X, Zhou W X, Tang L M, Chen K Q 2016 Appl. Phys. Lett. 109 23101 Google Scholar
[34]	Chen X K, Liu J, Peng Z H, Du D, Chen K Q 2017 Appl. Phys. Lett. 110 91907 Google Scholar
[35]	Xie G F, Ding D, Zhang G 2018 Adv. Phys. X 3 1480417
[36]	Kazan M, Guisbiers G, Pereira S, Correia M R, Masri P, Bruyant A, Volz S, Royer P 2010 J. Appl. Phys. 107 83503 Google Scholar
[37]	Ju Y S, Goodson K E 1999 Appl. Phys. Lett. 74 3005 Google Scholar
[38]	Evgrafov A, Maute K, Yang R G, Dunn M L 2009 Int. J. Numer. Meth. Eng. 77 285 Google Scholar
[39]	Murthy J Y, Mathur S R 2002 J. Heat Transf. 124 1176 Google Scholar
[40]	Narumanchi S V, Murthy J Y, Amon C H 2003 J. Heat Transf. 125 896 Google Scholar
[41]	Hamian S, Yamada T, Faghri M, Park K 2015 Int. J. Heat Mass Transf. 80 781 Google Scholar
[42]	Majumdar A 1993 J. Heat Transf. 115 7 Google Scholar
[43]	Chen G 1998 Phys. Rev. B 57 14958 Google Scholar
[44]	Sobolev S L 2018 Phys. Rev. E 97 22122 Google Scholar
[45]	华钰超, 董源, 曹炳阳 2013 62 244401 Google Scholar Hua Y C, Dong Y, Cao B Y 2013 Acta Phys. Sin. 62 244401 Google Scholar
[46]	Hua Y C, Cao B Y 2016 Int. J. Heat Mass Transf. 92 995 Google Scholar
[47]	Peterson R B 1994 J. Heat Transf. 116 815 Google Scholar
[48]	杜建镔 2015 结构优化及其在振动和声学设计中的应用 (北京: 清华大学出版社) 第115页 Du J B 2015 Structural Optimization and Its Applications in Vibration and Acoustic Designs (Beijing: Tsinghua University Press) p115 (in Chinese)
[49]	Bendsøe M P 1989 Struct. Optimization 1 193 Google Scholar
[50]	Sigmund O, Petersson J 1998 Struct. Optimization 16 68 Google Scholar
[51]	Zhang Y C, Liu S T 2008 Prog. Nat. Sci. 18 665 Google Scholar
[52]	Petersson J, Sigmund O 1998 Int. J. Numer. Meth. Eng. 41 1417 Google Scholar
[53]	Bendsoe M P, Sigmund O 2004 Topology Optimization: Theory, Methods, and Applications (Berlin: Springer) p17
[54]	Svanberg K 1987 Int. J. Numer. Meth. Eng. 24 359 Google Scholar
[55]	Hua Y C, Cao B Y 2018 J. Appl. Phys. 123 114304 Google Scholar
[56]	Alaili K, Ordonez-Miranda J, Ezzahri Y 2018 Int. J. Therm. Sci. 131 40 Google Scholar

[1]	Feng Jing-Sen, Min Jing-Chun. Lattice Boltzmann method simulation of two-phase flow in horizontal channel. Acta Physica Sinica, 2023, 72(8): 084701. doi: 10.7498/aps.72.20222421
[2]	Luo Tian-Lin, Ding Ya-Fei, Wei Bao-Jie, Du Jian-Ying, Shen Xiang-Ying, Zhu Gui-Mei, Li Bao-Wen. Phononic thermal conduction and thermal regulation in low-dimensional micro-nano scale systems: Nonequilibrium statistical physics problems from chip heat dissipation. Acta Physica Sinica, 2023, 72(23): 234401. doi: 10.7498/aps.72.20231546
[3]	Qiu Yu-Jun, Li Heng-Xuan, Li Ya-Tao, Huang Chun-Pu, Li Wei-Hua, Zhang Xu-Tao, Liu Ying-Guang. Nanodot embedding based optimization of interfacial thermal conductance. Acta Physica Sinica, 2023, 72(11): 113102. doi: 10.7498/aps.72.20230314
[4]	Liu Jin-Pin, Wang Bing-Zhong, Chen Chuan-Sheng, Wang Ren. Inverse design of microwave waveguide devices based on deep physics-informed neural networks. Acta Physica Sinica, 2023, 72(8): 080201. doi: 10.7498/aps.72.20230031
[5]	Shi Peng-Fei, Ma Xin-Ying, Xiang Chuan, Zhao Hong-Ge, Li Yuan, Gao Ren-Jing, Liu Shu-Tian. Topology optimization design of dual-channel metasurface structure with controllable amplitude of retroreflection and mirror reflection. Acta Physica Sinica, 2023, 72(24): 247801. doi: 10.7498/aps.72.20230775
[6]	Sang Di, Xu Ming-Feng, An Qiang, Fu Yun-Qi. Freeform wavelength division multiplexing metagrating based on topology optimization. Acta Physica Sinica, 2022, 71(22): 224204. doi: 10.7498/aps.71.20221013
[7]	Zhang Qian-Yi, Wei Hua-Jian, Li Hua-Bing. Multi-segment lymphatic vessel model based on lattice Boltzmann method. Acta Physica Sinica, 2021, 70(21): 210501. doi: 10.7498/aps.70.20210514
[8]	Qiu Ke-Peng, Luo Yue, Zhang Wei-Hong. Analysis and design of new chiral metamaterials with asymmetric transmission characteristics. Acta Physica Sinica, 2020, 69(21): 214101. doi: 10.7498/aps.69.20200728
[9]	Jia Ding, Ge Yong, Yuan Shou-Qi, Sun Hong-Xiang. Dual-band acoustic topological insulator based on honeycomb lattice sonic crystal. Acta Physica Sinica, 2019, 68(22): 224301. doi: 10.7498/aps.68.20190951
[10]	Mo Man-Man, Ma Wu-Wei, Pang Yong-Qiang, Chen Run-Hua, Zhang Xiao-Mei, Liu Zhao-Tang, Li Xiang, Guo Wan-Tao. Broadband absorbent materials based on topology optimization design. Acta Physica Sinica, 2018, 67(21): 217801. doi: 10.7498/aps.67.20181170
[11]	Feng Dai-Li, Feng Yan-Hui, Shi Jun. Lattice Boltzamn model of phonon heat conduction in mesoporous composite material. Acta Physica Sinica, 2016, 65(24): 244401. doi: 10.7498/aps.65.244401
[12]	Luo Xiao-Yuan, Li Hao, Ma Ju-Hai. Topology optimization algorithm for wireless networks based on the algebraic properties of minimum rigid graph. Acta Physica Sinica, 2016, 65(24): 240201. doi: 10.7498/aps.65.240201
[13]	Liu Fei-Fei, Wei Shou-Shui, Wei Chang-Zhi, Ren Xiao-Fei. Use of velocity source immersed boundary-lattice Boltzmann method to study bionic micro-fluidic driving model. Acta Physica Sinica, 2014, 63(19): 194704. doi: 10.7498/aps.63.194704
[14]	Xue Ze, Shi Juan, Wang Li-Long, Zhou Jin-Yang, Tan Hui-Li, Li Hua-Bing. The lattice Boltzmann simulation of suspended particle movement in a tapered tube. Acta Physica Sinica, 2013, 62(8): 084702. doi: 10.7498/aps.62.084702
[15]	Sun Dong-Ke, Xiang Nan, Chen Ke, Ni Zhong-Hua. Lattice Boltzmann modeling of particle inertial migration in a curved channel. Acta Physica Sinica, 2013, 62(2): 024703. doi: 10.7498/aps.62.024703
[16]	Chen Lin-Gen, Feng Hui-Jun, Xie Zhi-Hui, Sun Feng-Rui. Constructal entransy dissipation rate minimization of a disc on micro and nanoscales. Acta Physica Sinica, 2013, 62(13): 134401. doi: 10.7498/aps.62.134401
[17]	Zhou Feng-Mao, Sun Dong-Ke, Zhu Ming-Fang. Lattice Boltzmann modelling of liquid-liquid phase separation of monotectic alloys. Acta Physica Sinica, 2010, 59(5): 3394-3401. doi: 10.7498/aps.59.3394
[18]	Shi Juan, Li Hua-Bing, Wang Wen-Xia, Qiu Bing. Lattice Boltzmann simulation of surface hydrophobicity with nano-structure. Acta Physica Sinica, 2010, 59(12): 8371-8376. doi: 10.7498/aps.59.8371
[19]	Shi Juan, Li Jian, Qiu Bing, Li Hua-Bing. Lattice Boltzmann simulation of particles moving in a vortex flow. Acta Physica Sinica, 2009, 58(8): 5174-5178. doi: 10.7498/aps.58.5174
[20]	Deng Min-Yi, Shi Juan, Li Hua-Bing, Kong Ling-Jiang, Liu Mu-Ren. Lattice Boltzmann method for the production and evolution of spiral waves. Acta Physica Sinica, 2007, 56(4): 2012-2017. doi: 10.7498/aps.56.2012

Catalog

Vol. 68, Issue 20 - 2019-10-20

Metrics

Abstract views: 9781
PDF Downloads: 179
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板