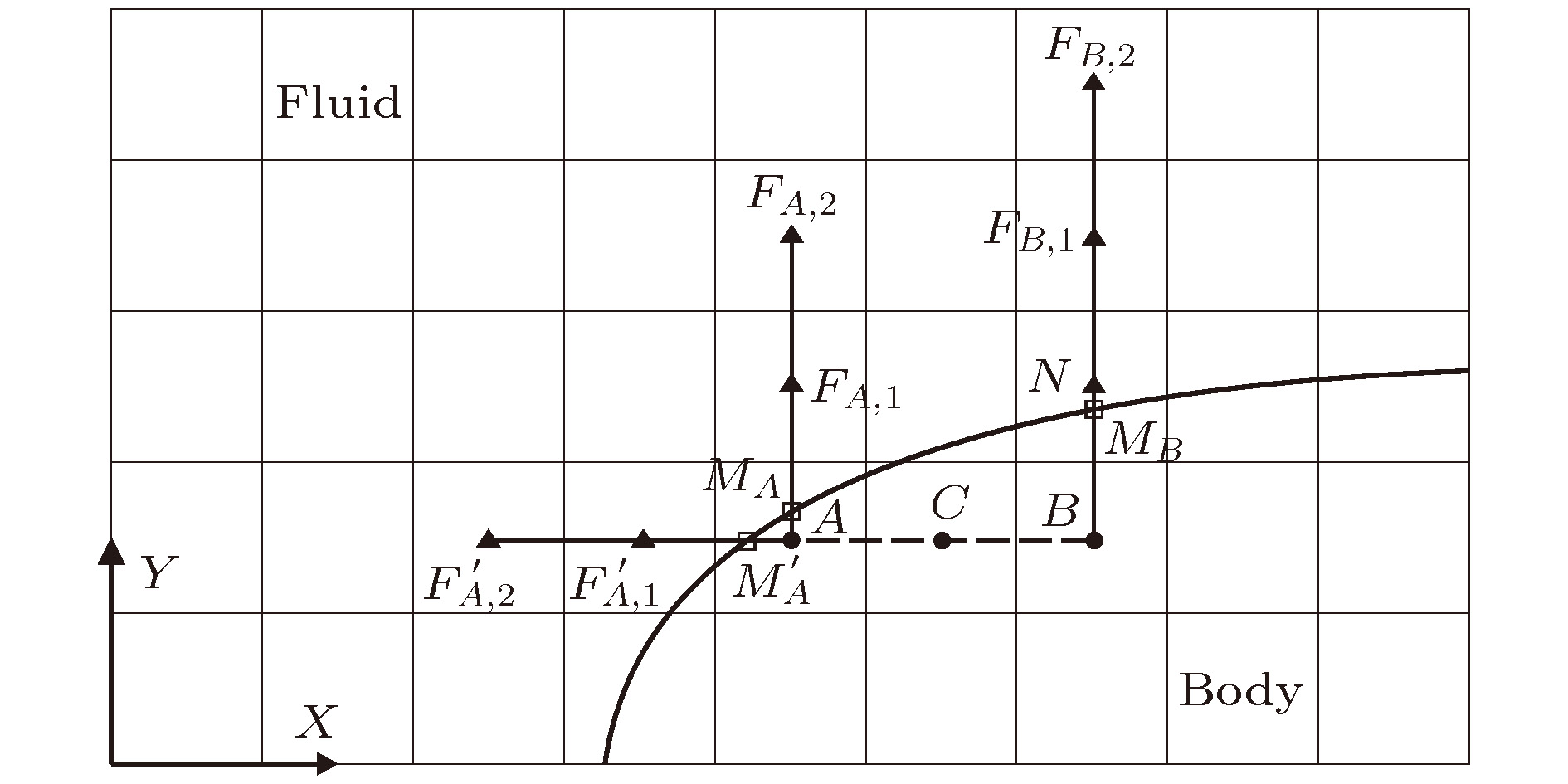
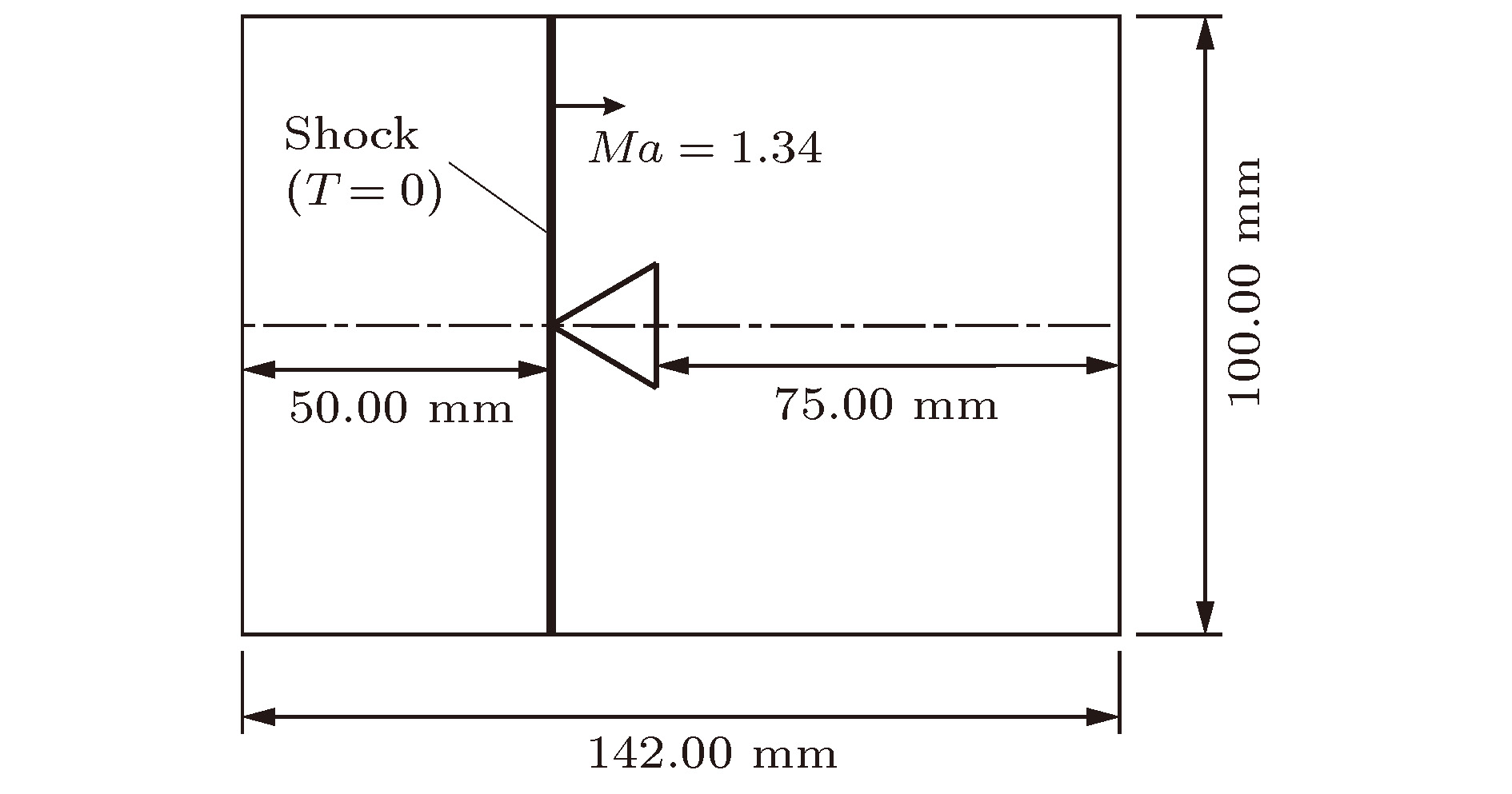
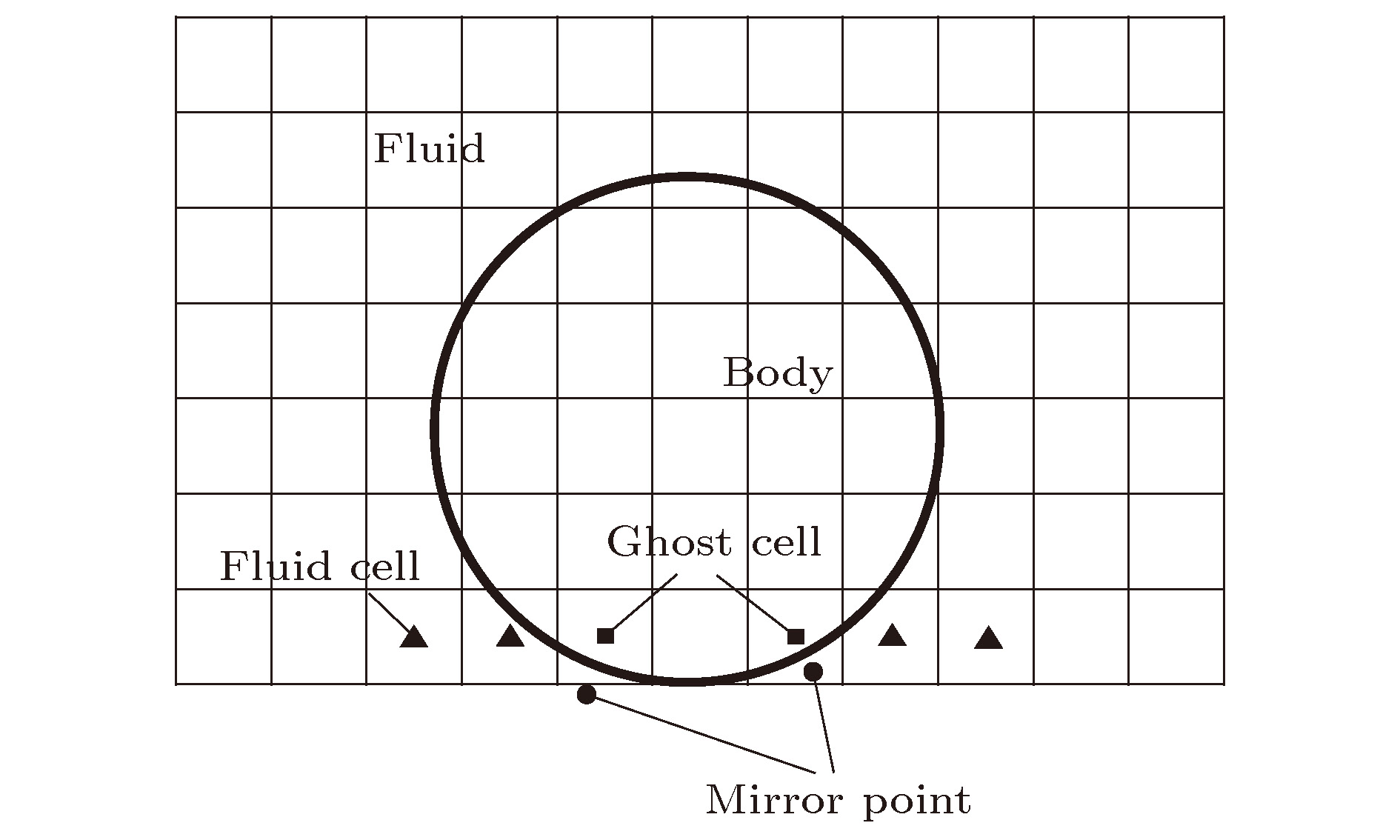
-
In this paper, an improved ghost cell method is implemented to solve flow problems with static and moving boundary. The two-dimensional unsteady compressible Euler equations are discretized on a fixed Cartesian grid by the finite volume method, and the monotonic upstream-centered scheme for conservation law scheme is adopted to obtain the second-order precision by reconstructing the numerical fluxes computed by the AUSM + (advection upstream splitting method +) scheme. In time discretization, the explicit third-order total-variation-diminishing Runge-Kutta method is considered. To simplify the assignment method for the ghost cells and deal with the slit problem, the cells in the flow field are selected as the mirror points, which avoids complex interpolations. For preventing non-physical solutions when the mirror point is very close to the boundary, the current mirror point will be replaced by another one, which is regarded as the second flow field cell located in the direction away from the boundary. Moreover, properties of a ghost cell along the X and Y direction are computed respectively, and then the final property is obtained by using a weighted average method, where the weight is determined by the distance between the ghost cell and corresponding boundary point. In this method, the selection of mirror points does not change abruptly for adjacent ghost cells, and therefore, no kink occurs. Furthermore, considering the gradient of the variable near the boundary, an extended scheme of the improved ghost cell method is achieved, which can deal with the flow problems with moving boundaries. When computing the property of a ghost cell by using the extended scheme, the result may be wrong if the location of a shock is just between two mirror points. In view of the problem above, a shock monitor is implemented to switch to the appropriate approach, that is, when the monitor detects a shock between mirror points, the extended scheme will be replaced by the original ghost cell method. Two typical test cases are investigated to validate the accuracy of the proposed method. The first test case is the Schardin’s problem, in which a shock impinges on a finite wedge and is reflected and diffracted. The results at different grid sizes are obtained, and good agreement with experiment results as well as the previous numerical results is achieved, which shows that the improved ghost cell method can offer the same precision as the body-fitted grid method. The second test case is the cylinder lift-off problem involving moving boundaries and the slit problem. Good agreement with the previous results of a high-order complex ghost cell method shows that the improved simple ghost cell method can meet the requirement for dealing with flow problems with moving boundaries.
-
Keywords:
- ghost cell method /
- static and moving boundary /
- Cartesian grid /
- Euler
[1] 张妮, 刘丁, 冯雪亮 2018 67 218701
Google Scholar
Zhang N, Liu D, Feng X L 2018 Acta Phys. Sin. 67 218701
Google Scholar
[2] 李强, 李五明 2016 65 064601
Google Scholar
Li Q, Li W M 2016 Acta Phys. Sin. 65 064601
Google Scholar
[3] 辛建建, 石伏龙, 金秋 2017 66 044704
Google Scholar
Xin J J, Shi F L, Jin Q 2017 Acta Phys. Sin. 66 044704
Google Scholar
[4] Bennett W P, Nikiforakis N, Klein R 2018 J. Comput. Phys. 368 333
Google Scholar
[5] Mittal R, Iaccarino G 2005 Ann. Rev. Fluid Mech. 37 239
Google Scholar
[6] 吴晓笛, 刘华坪, 陈浮 2017 66 224702
Google Scholar
Wu X D, Liu H P, Chen F 2017 Acta Phys. Sin. 66 224702
Google Scholar
[7] Majumdar S, Iaccarino G, Durbin P 2001 Ann. Res. Briefs 30 353
[8] Tan S, Shu C W 2011 J. Comput. Phys. 230 6023
Google Scholar
[9] Nakahashi K 2013 Eur. J. Mech. B: Fluids 40 75
Google Scholar
[10] Tseng Y H, Ferziger J H 2003 J. Comput. Phys. 192 593
Google Scholar
[11] Dadone A, Grossman B 2007 Comput. Fluids 36 1513
Google Scholar
[12] Farooq M A, Müller B, Skøien A A 2013 Comput. Fluids 82 50
Google Scholar
[13] Chi C, Lee B J, Im H G 2017 Int. J. Numer. Meth. Fluids 83 132
Google Scholar
[14] Forrer H, Berger M 1999 Internat. Ser. Numer. Math. 129 315
[15] Lee J, Kim J, Choi H, Yang K S 2011 J. Comput. Phys. 230 2677
Google Scholar
[16] Lee J, You D 2013 J. Comput. Phys. 233 295
Google Scholar
[17] Peter S, De A K 2016 Sādhanā 41 441
Google Scholar
[18] 胡偶, 赵宁, 刘剑明, 王东红 2011 空气动力学学报 29 491
Google Scholar
Hu O, Zhao N, Liu J M, Wang D H 2011 Acta Aerodyn. Sin. 29 491
Google Scholar
[19] 金利云 2012 硕士学位论文 (南京: 南京航空航天大学)
Jin L Y 2012 M. S. Thesis (Nanjing: Nanjing University of Aeronautics and Astronautics) (in Chinese)
[20] Jameson A, Schmidt W, Turkel E 1981 14th Fluid and Plasma Dynamics Conference Palo Alto, CA, USA, June 23−25, 1981 p1259
[21] Liou M S 1995 12th Computational Fluid Dynamics Conference San Diego, CA, USA, June 19−22, 1995 p1701
[22] Leer B V 1974 J. Comput. Phys. 14 361
Google Scholar
[23] Shu C W, Osher S 1988 J. Comput. Phys. 77 439
[24] Schardin H 1957 J. Photo. Sci. 5 19
[25] Chang S M, Chang K S 2000 Shock Waves 10 333
[26] Arienti M, Hung P, Morano E, Shepherd J E 2003 J. Comput. Phys. 185 213
-
图 1 狭缝问题(物体底部虚拟单元的镜像点缺乏合适的插值点)
Figure 1. Slit problem, which is caused by the lack of interpolation points of the mirror points.
图 2 改进的虚拟单元法示意图
Figure 2. Demonstration of the improved ghost cell method.
图 3 SGCM中出现的扭曲现象(标记区域)以及采用ISGCM求得的圆柱表面压力系数与采用SGCM、MSGCM、贴体网格得到的结果的对比
Figure 3. Kink noted in the picture, which is happened when using the SGCM, and the comparison of the pressure coefficients obtained by using SGCM, MSGCM, ISGCM and the body fitted mesh.
图 4 推广的改进型虚拟单元法示意图
Figure 4. The demonstration of the extended ISGCM.
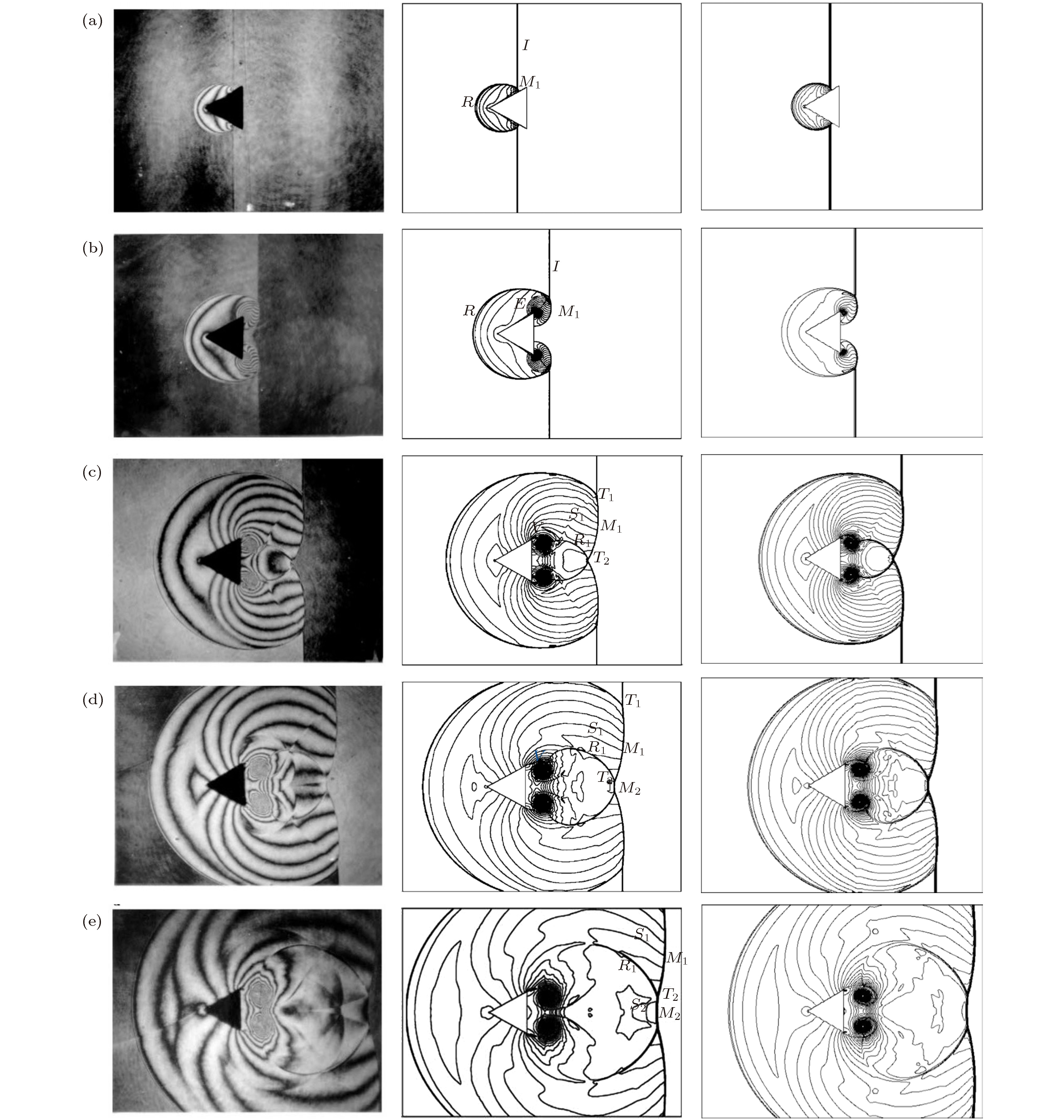
图 6 不同时刻下的实验结果(左)、Chang等[25]计算所得的密度等值线(中)和采用ISGCM计算所得的密度等值线(右) (a) T = 28 μs; (b) T = 53 μs; (c) T = 102 μs; (d) T = 130 μs; (e) T = 172 μs
Figure 6. Experimental results (left), Chang et al.[25] results and the density contour computed by us (right): (a) T = 28 μs; (b) T = 53 μs; (c) T = 102 μs; (d) T = 130 μs; (e) T = 172 μs.
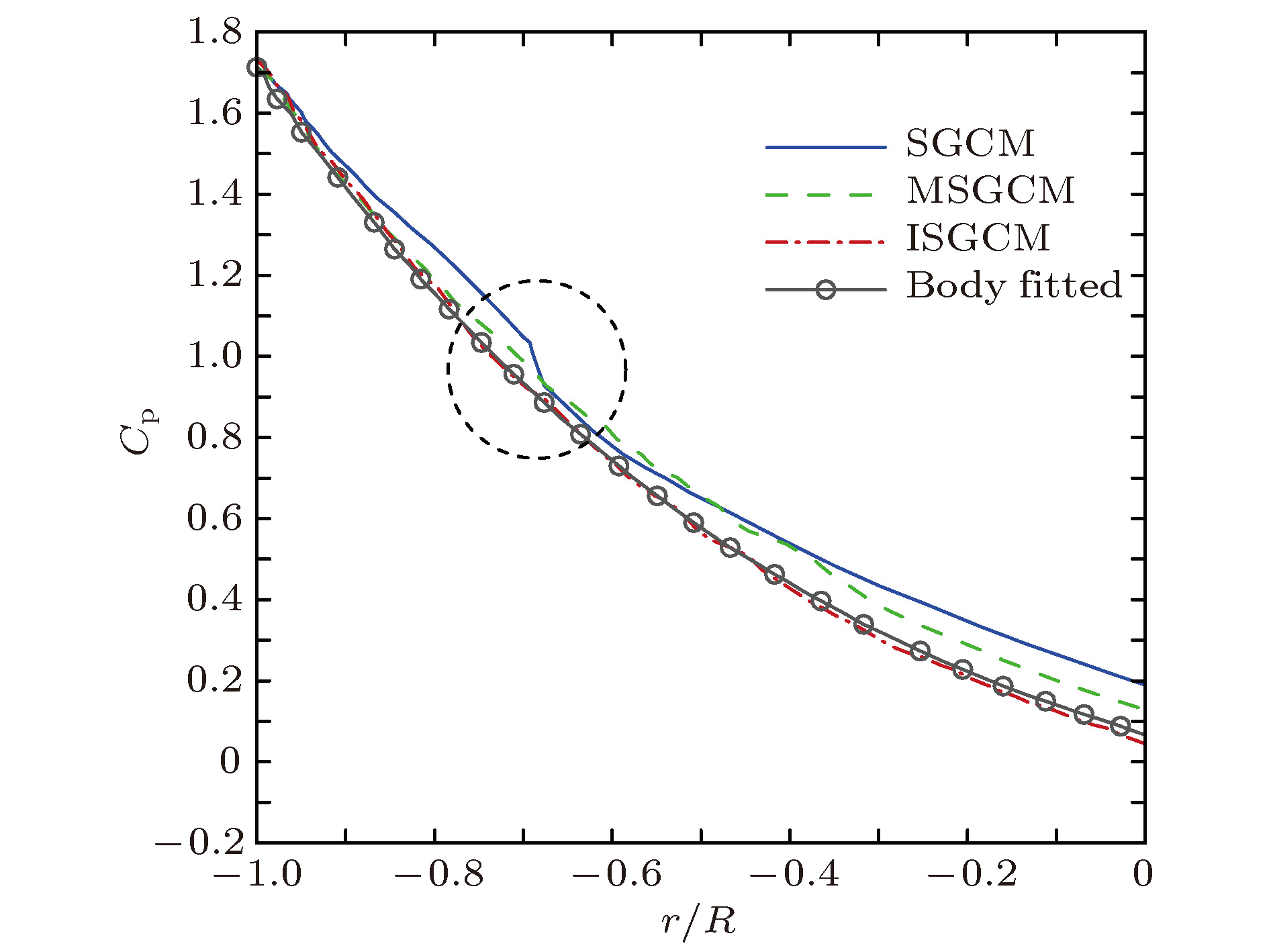
图 7 (a)计算所得沿模型中间对称面上的密度分布与Chang等[25]的计算结果以及实验数据的对比; (b)沿模型中间对称面上的马赫数分布与Chang等[25]的计算结果的对比
Figure 7. (a) Comparison of the density distribution along the symmetry plane between the results obtained by this paper and Chang et al.[25] as well as the experiment; (b) the comparison of the Mach number distribution along the symmetry plane between the results obtained by this paper and the results of Chang et al.[25].
图 8 激波抬升轻质圆柱问题的模型描述
Figure 8. Physical model of the cylinder lift-off problem.
表 1 不同网格量下T = 0.1641和0.30085时圆柱中心的坐标
Table 1. Position of the center of the cylinder at T = 0.1641 and 0.30085.
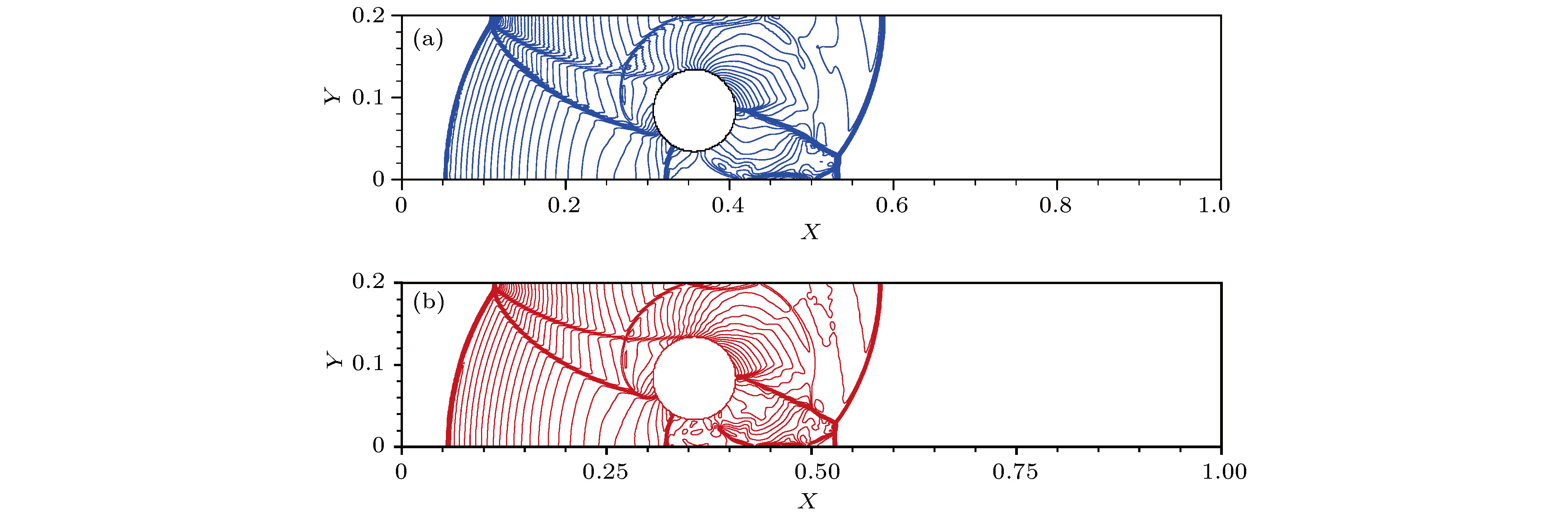
网格量 T = 0.1641 T = 0.30085 X/10–1 Y/10–2 X/10–1 Y/10–1 200 × 200 3.6294 7.9990 6.5686 1.3654 400 × 400 3.5885 8.2377 6.3987 1.4292 600 × 600 3.5841 8.3379 6.3873 1.4475 800 × 800 3.5828 8.3469 6.3839 1.4490 
DownLoad: CSV
-
[1] 张妮, 刘丁, 冯雪亮 2018 67 218701
Google Scholar
Zhang N, Liu D, Feng X L 2018 Acta Phys. Sin. 67 218701
Google Scholar
[2] 李强, 李五明 2016 65 064601
Google Scholar
Li Q, Li W M 2016 Acta Phys. Sin. 65 064601
Google Scholar
[3] 辛建建, 石伏龙, 金秋 2017 66 044704
Google Scholar
Xin J J, Shi F L, Jin Q 2017 Acta Phys. Sin. 66 044704
Google Scholar
[4] Bennett W P, Nikiforakis N, Klein R 2018 J. Comput. Phys. 368 333
Google Scholar
[5] Mittal R, Iaccarino G 2005 Ann. Rev. Fluid Mech. 37 239
Google Scholar
[6] 吴晓笛, 刘华坪, 陈浮 2017 66 224702
Google Scholar
Wu X D, Liu H P, Chen F 2017 Acta Phys. Sin. 66 224702
Google Scholar
[7] Majumdar S, Iaccarino G, Durbin P 2001 Ann. Res. Briefs 30 353
[8] Tan S, Shu C W 2011 J. Comput. Phys. 230 6023
Google Scholar
[9] Nakahashi K 2013 Eur. J. Mech. B: Fluids 40 75
Google Scholar
[10] Tseng Y H, Ferziger J H 2003 J. Comput. Phys. 192 593
Google Scholar
[11] Dadone A, Grossman B 2007 Comput. Fluids 36 1513
Google Scholar
[12] Farooq M A, Müller B, Skøien A A 2013 Comput. Fluids 82 50
Google Scholar
[13] Chi C, Lee B J, Im H G 2017 Int. J. Numer. Meth. Fluids 83 132
Google Scholar
[14] Forrer H, Berger M 1999 Internat. Ser. Numer. Math. 129 315
[15] Lee J, Kim J, Choi H, Yang K S 2011 J. Comput. Phys. 230 2677
Google Scholar
[16] Lee J, You D 2013 J. Comput. Phys. 233 295
Google Scholar
[17] Peter S, De A K 2016 Sādhanā 41 441
Google Scholar
[18] 胡偶, 赵宁, 刘剑明, 王东红 2011 空气动力学学报 29 491
Google Scholar
Hu O, Zhao N, Liu J M, Wang D H 2011 Acta Aerodyn. Sin. 29 491
Google Scholar
[19] 金利云 2012 硕士学位论文 (南京: 南京航空航天大学)
Jin L Y 2012 M. S. Thesis (Nanjing: Nanjing University of Aeronautics and Astronautics) (in Chinese)
[20] Jameson A, Schmidt W, Turkel E 1981 14th Fluid and Plasma Dynamics Conference Palo Alto, CA, USA, June 23−25, 1981 p1259
[21] Liou M S 1995 12th Computational Fluid Dynamics Conference San Diego, CA, USA, June 19−22, 1995 p1701
[22] Leer B V 1974 J. Comput. Phys. 14 361
Google Scholar
[23] Shu C W, Osher S 1988 J. Comput. Phys. 77 439
[24] Schardin H 1957 J. Photo. Sci. 5 19
[25] Chang S M, Chang K S 2000 Shock Waves 10 333
[26] Arienti M, Hung P, Morano E, Shepherd J E 2003 J. Comput. Phys. 185 213
DownLoad:
Catalog
Metrics
- Abstract views: 7371
- PDF Downloads: 48
- Cited By: 0
