-
The potential energy curves, dipole moments, and transition dipole moments for the
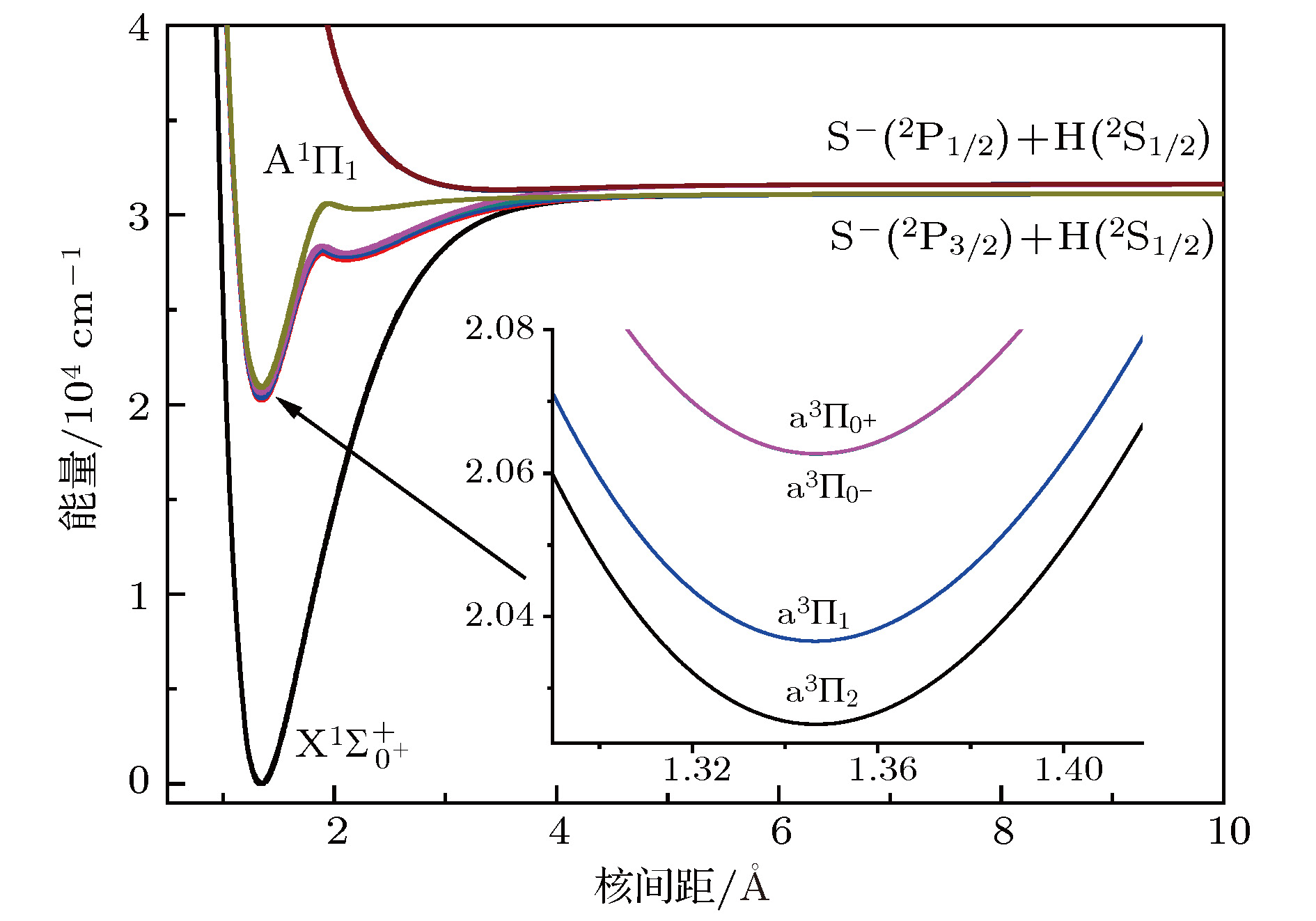
${{\rm{X}}^1}{\Sigma ^ + }$ ,${{\rm{a}}^3}\Pi $ , and${{\rm{A}}^1}\Pi $ electronic state of sulfur hydride anion (SH–) are calculated by using the multi-reference configuration interaction method plus Davidson corrections (MRCI+Q) with all-electron basis set. The scalar relativistic corrections and core-valence correlations are also considered. In the CASSCF calculations, H(1s) and S(3s3p4s) shells are chosen as active space, and the rest orbitals S(1s2s2p) as closed-shell. In the MRCI+Q calculations, the S(1s2s2p) shells are used for the core-valence correlation. Spectroscopic parameters, Einstein spontaneous emission coefficient, Franck-Condon factors, and spontaneous radiative lifetimes are obtained by using Le Roy’s LEVEL8.0 program. The calculated spectroscopic parameters are in good agreement with available experimental data and theoretical values. Spin-orbit coupling (SOC) effects are evaluated with Breit-Pauli operators at the MRCI+Q level. Transition dipole moments (TDMs) for the${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ ,${{\rm{a}}^3}{\Pi _{{0^ + }}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ ,${{\rm{a}}^3}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ ,${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{a}}^3}{\Pi _{{0^ + }}}$ and${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{a}}^3}{\Pi _1}$ transitions are also calculated. The strength for the${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ is the strongest in these five transitions, the value of TDM at Re is –1.3636 D. We find that the value of TDM for the${{\rm{a}}^3}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ transition at Re is 0.5269 D. Therefore, this transition must be taken into account to build the scheme of laser-cooled SH– anion. Highly diagonally distributed Franck-Condon factor f00 for the${{\rm{a}}^3}{\Pi _1}(\nu ' = 0) \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ $ (\nu '' = 0)$ transition is 0.9990 and the value for the${{\rm{A}}^1}{\Pi _1}(\nu ' = 0) \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + (\nu '' = 0)$ transition is 0.9999. Spontaneous radiative lifetimes of$\tau \left( {{{\rm{a}}^3}{\Pi _1}} \right)= 1.472 \;{\text{μ}}{\rm{s}}$ and$\tau \left( {{{\rm{A}}^1}{\Pi _1}} \right)=0.188 \;{\text{μ}}{\rm{s}}$ are obtained, which can ensure that laser cools SH– anion rapidly. To drive the${{\rm{a}}^3}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ and${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ transitions, just one laser wavelength is required. The wavelengths are 492.27 nm and 478.57 nm for two transitions, respectively. Notably, the influences of the intervening states${{\rm{a}}^3}{\Pi _1}$ and${{\rm{a}}^3}{\Pi _{{0^{\rm{ + }}}}}$ on the${{\rm{A}}^1}{\Pi _1} \leftrightarrow {X^1}\Sigma _{{0^ + }}^ + $ transition are small enough to implement a laser cooling project. A spin-forbidden transition and a three-electronic-level transition optical scheme of laser-cooled SH– anion are constructed, respectively. In addition, the Doppler temperatures and recoil temperatures for the${{\rm{a}}^3}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ and${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ transitions of laser-cooled SH– anion are also obtained, respectively.-
Keywords:
- spin-orbit coupling /
- Franck-Condon factors /
- spontaneous radiative lifetimes /
- laser cooling
[1] Shuman E S, Barry J F, DeMille D 2010 Nature 467 820
Google Scholar
[2] Zhelyazkova V, Cournol A, Wall T E, Matsushima A, Hudson J J, Hinds E A, Tarbutt M R, Sauer B E 2014 Phys. Rev. A 89 053416
Google Scholar
[3] Hummon M T, Yeo M, Stuhl B K, Collopy A L, Xia Y, Ye J 2013 Phys. Rev. Lett. 110
Google Scholar
[4] 张云光, 张华, 窦戈, 徐建刚 2017 66 233101
Google Scholar
Zhang Y G, Zhang H, Dou G, Xu J G 2017 Acta Phys. Sin. 66 233101
Google Scholar
[5] Gao Y, Gao T 2014 Phys. Rev. A 90 052506
Google Scholar
[6] Wan M, Shao J, Huang D, Jin C, Yu Y, Wang F 2015 Phys. Chem. Chem. Phys. 17 26731
Google Scholar
[7] Wan M, Shao J, Gao Y, Huang D, Yang J, Cao Q, Jin C, Wang F 2015 J. Chem. Phys. 143 024302
Google Scholar
[8] Gao Y, Gao T 2015 Phys. Chem. Chem. Phys. 17 10830
Google Scholar
[9] 李亚超, 孟腾飞, 李传亮等 2017 66 163101
Google Scholar
Li Y C, Meng T F, Li C L, et al. 2017 Acta Phys. Sin. 66 163101
Google Scholar
[10] Zhang Q, Yang C, Wang M, Ma X, Liu W 2017 Spectrochim. Acta, Part A 182 130
Google Scholar
[11] Zhang Q, Yang C, Wang M, Ma X, Liu W 2017 Spectrochim. Acta, Part A 185 365
Google Scholar
[12] Wan M, Huang D, Yu Y, Zhang Y 2017 Phys. Chem. Chem. Phys. 19 27360
Google Scholar
[13] Steiner B 1968 J. Chem. Phys. 49 5097
Google Scholar
[14] Breyer F, Frey P, Hotop H 1981 Z. Phys. 300 7
Google Scholar
[15] Janousek B K, Brauman J I 1981 Phys. Rev. A 23 1673
Google Scholar
[16] Cade P 1967 J. Chem. Phys. 47 2390
Google Scholar
[17] Rosmus P, Meyer W 1978 J. Chem. Phys. 69 2745
Google Scholar
[18] Senekowitsch J, Werner H J, Rosmus P, Reinsch E A, Oneil S V 1985 J. Chem. Phys. 83 4661
Google Scholar
[19] Vamhindi B S D R, Nsangou M 2016 Mol. Phys. 114 2204
Google Scholar
[20] Werner H J, Knowles P J 1988 J. Chem. Phys. 89 5803
Google Scholar
[21] Knowles P J, Werner H J 1988 Chem. Phys. Lett. 145 514
Google Scholar
[22] Langhoff S R, Davidson E R 1974 Int. J. Quantum Chem. 8 61
Google Scholar
[23] Knowles P J, Werner H J 1985 J. Chem. Phys. 82 5053
Google Scholar
[24] Knowles P J, Werner H J 1985 Chem. Phys. Lett. 115 259
Google Scholar
[25] Douglas M, Kroll N M 1974 Ann. Phys. 82 89
Google Scholar
[26] Hess B A 1986 Phys. Rev. A 33 3742
Google Scholar
[27] Berning A, Schweizer M, Werner H J, Knowles P J, Palmieri P 2000 Mol. Phys. 98 1823
Google Scholar
[28] Werner H J, Knowles P J, Lindh R, et al. MOLPRO, version 2010.1, a package of ab initio programs, 2010, see http://www.molpro.net [2018-11-15]
[29] Peterson K A, Dunning Jr T H 2002 J. Chem. Phys. 117 10548
Google Scholar
[30] Dunning Jr T H 1989 J. Chem. Phys. 90 1007
Google Scholar
[31] Murrell J N, Sorbie K S. 1974 J Chem. Soc., Faraday Trans. 70 1552
Google Scholar
[32] Le Roy R J Level 8.0: A Computer Program for Solving the Radial Schrödinger Equation for Bound and Quasibound Levels (Waterloo: University of Waterloo) Chemical Physics Research Report CP-663
[33] Lykke K R, Murray K K, Lineberger W C 1991 Rhys. Rev. A 43 6104
Google Scholar
[34] Hotop H, Lineberger W C 1985 J. Phys. Chem. Ref. Data 14 731
Google Scholar
[35] Moore C E 1971 Atomic Energy Levels (Vol. 1) (Washington, DC: National Bureau of Standards Publications) p181
[36] Cohen-Tannoudji C N 1998 Rev. Phys. Mod. 70 707
Google Scholar
[37] Kobayashi J, Aikawa K, Oasa K, Inouye S 2014 Phys. Rev. A 89 021401
Google Scholar
-
图 1 SH–阴离子的
${{\rm{X}}^1}{\Sigma ^ + }$ ,${{\rm{a}}^3}\Pi $ ,${{\rm{A}}^1}\Pi $ ,${1^3}{\Sigma ^ + }$ 和${2^1}{\Sigma ^ + }$ 态的势能曲线Figure 1. Potential energy curves for the
${{\rm{X}}^1}{\Sigma ^ + }$ ,${{\rm{a}}^3}\Pi $ ,${{\rm{A}}^1}\Pi $ , and${2^1}{\Sigma ^ + }$ states of SH– anion.
图 2 SH–阴离子的
$\Omega$ 态的势能曲线Figure 2. Potential energy curves for the
$\Omega$ states of SH– anion.
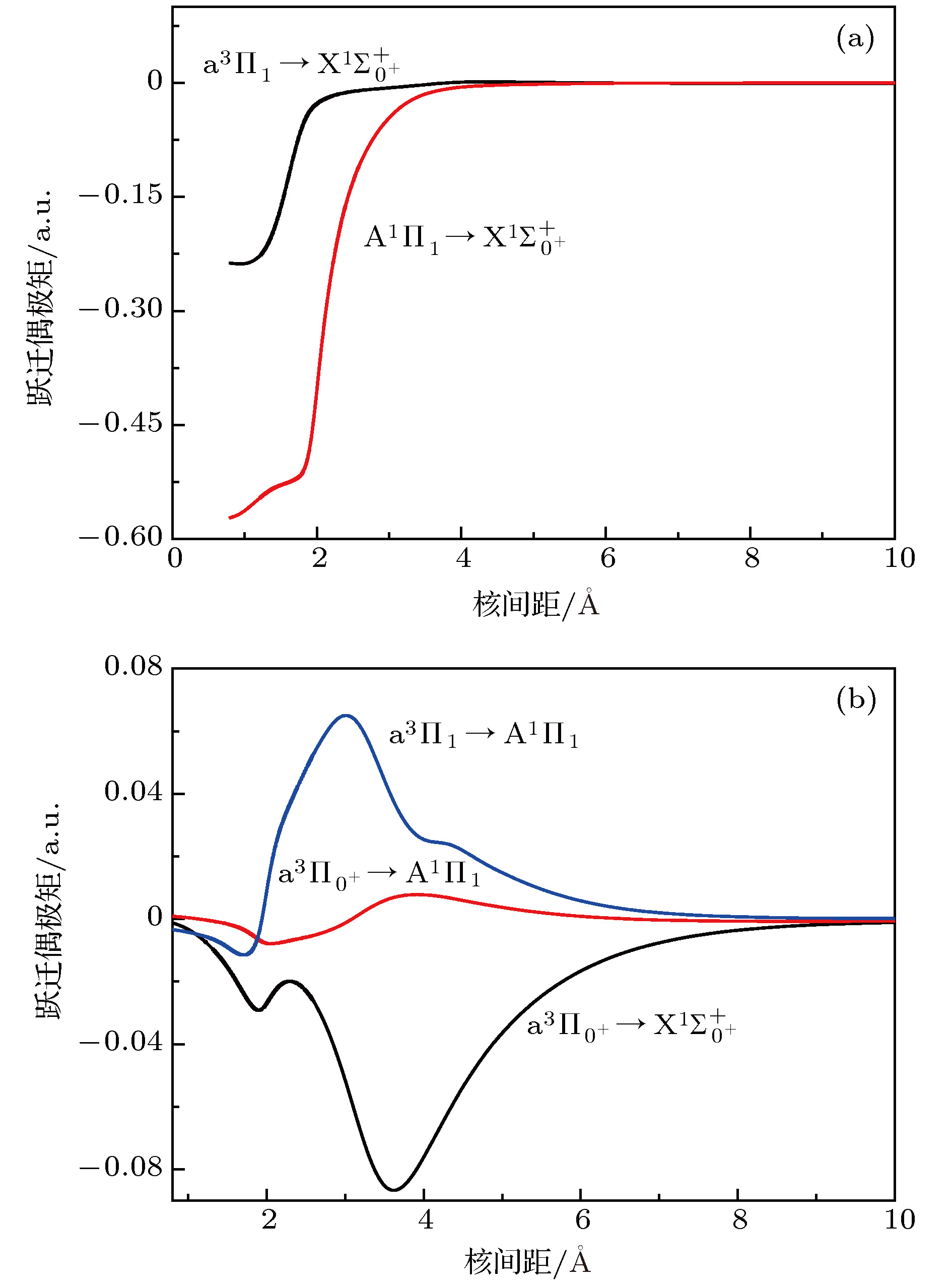
图 3 SH–阴离子的跃迁偶极矩 (a)
${{\rm{A}}^{1}}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 和${{\rm{a}}^3}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁; (b)${{\rm{a}}^{3}}{\Pi _{{0^ + }}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ ,${{\rm{A}}^1}{\Pi _1} \!\leftrightarrow\!{{\rm{a}}^3}{\Pi _{{0^ + }}}$ 和${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{a}}^3}{\Pi _1}$ 跃迁Figure 3. Transition dipole moments of SH– anion: (a) The
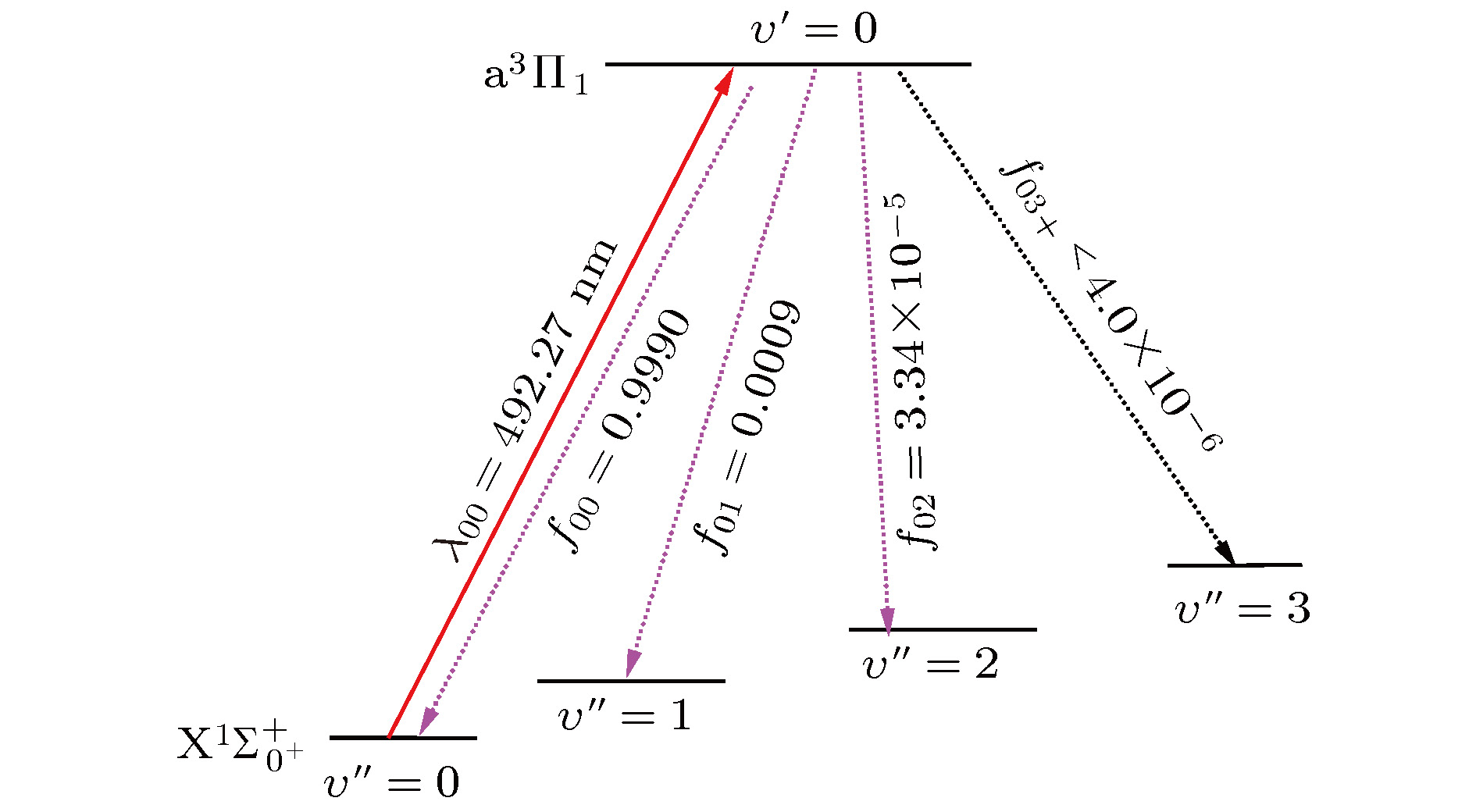
${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ and${{\rm{a}}^{3}}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ transitions; (b) the${{\rm{a}}^3}{\Pi _{{0^ + }}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ ,${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{a}}^3}{\Pi _{{0^ + }}}$ and${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{a}}^3}{\Pi _1}$ transitions.
图 4 采用
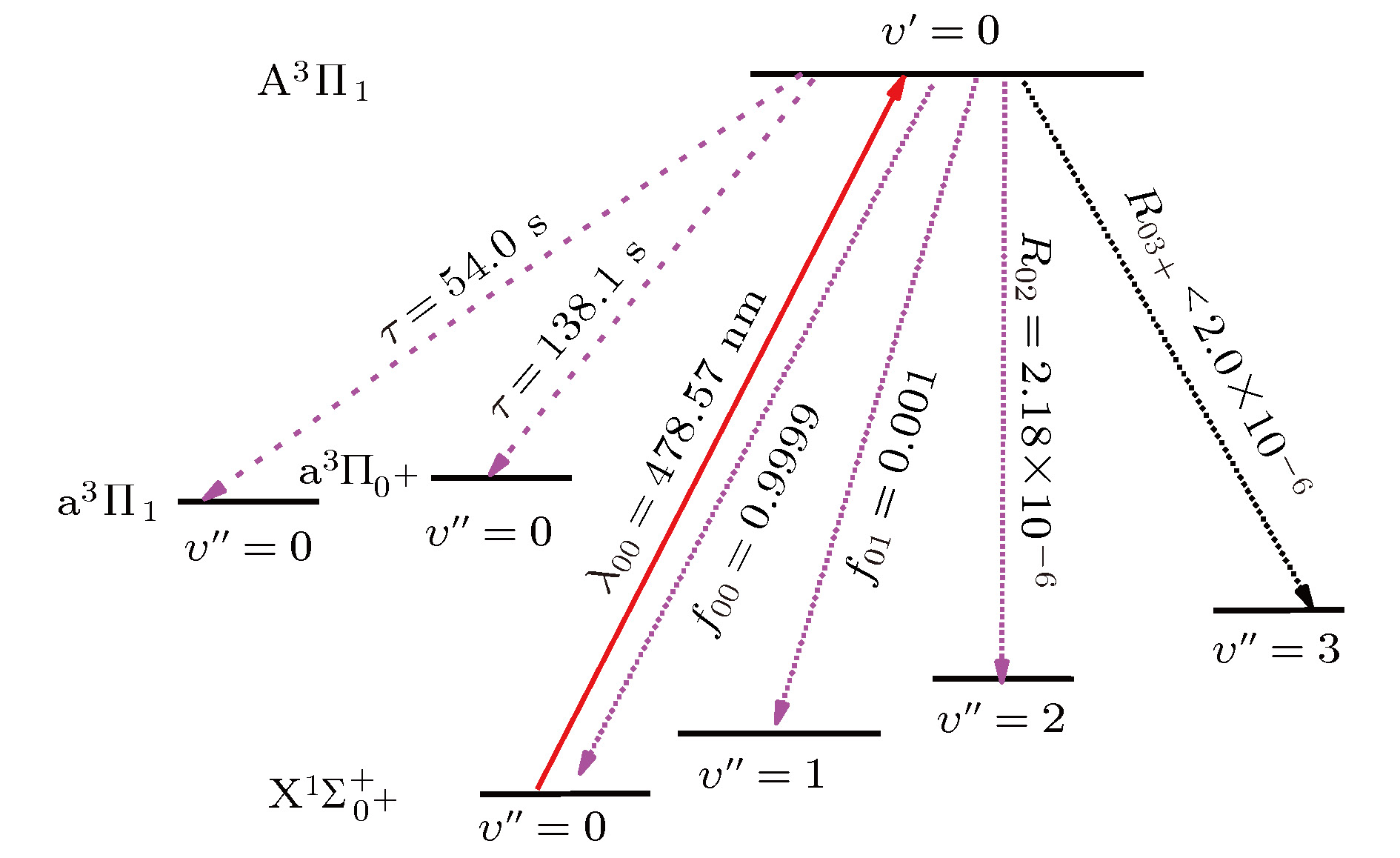
$\scriptstyle {{{\rm{a}}^3}{\Pi _1}}\leftrightarrow \scriptstyle {{{\rm{X}}^1}\Sigma _{{0^ + }}^ + }$ 跃迁进行激光冷却SH–阴离子的方案, 实线为所需激光, 虚线为自发辐射的弗兰克-康登因子Figure 4. Proposed laser cooling scheme for the
$ \scriptstyle{{{\rm{a}}^3}{\Pi _1}}\leftrightarrow$ $\scriptstyle {{{\rm{X}}^1}\Sigma _{{0^ + }}^ + }$ transition (solid line) and spontaneous decay.
图 5 采用
${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁进行激光冷却SH–阴离子的方案, 其中实线为所需激光, 虚线为自发辐射的弗兰克-康登因子Figure 5. Proposed laser cooling scheme for the
$ {{\rm{A}}^1}{\Pi _1} \leftrightarrow$ $ {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ transition (solid line) and spontaneous decay.表 1 SH-阴离子的
$\Lambda\text{-}\rm S$ 态的光谱常数Table 1. Spectroscopic parameters for the
$\Lambda\text{-}\rm S $ states of SH– anion.电子态 Re/Å $\omega_{\rm{e}}$/cm–1 $\omega_{\rm{e}}\chi_{\rm{e}}$/cm–1 Be/cm–1 De/eV Te/cm–1 RMS/cm–1 ${{\rm{X}}^1}{\Sigma ^ + }$ 本文工作 1.3435 2622.04 46.66 9.5590 3.8793 0 4.4107 实验值[13] 1.34—0.02 2700—300 9.46—0.32 实验值[14] 2648—110 9.39—0.3 理论值[17] 1.348 2642 52 9.49 3.902 0 理论值[18] 1.346 2637 52 9.52 理论值[19] 1.3440 2682.86 39.2 9.551 4.19 ${{\rm{a}}^3}\Pi $ 本文工作 第一势阱 1.3466 2583.61 73.22 9.5148 0.9598 20436.92 0.0604 理论值[19] 1.3746 1936.16 307.503 9.129 1.38 22082.7 本文工作 第二势阱 2.1021 778.72 133.34 3.9045 0.4356 27816.71 1.1556 ${{\rm{A}}^1}\Pi $ 本文工作 第一势阱 1.3441 2626.59 61.51 9.5511 1.1848 20852.70 0.0474 理论值[19] 1.3432 2554.97 44.186 9.561 1.33 22225.2 本文工作 第二势阱 2.2430 424.80 36.810 3.4296 0.1217 30299.28 0.3277 
DownLoad: CSV
表 2 SH–阴离子的
$\Omega$ 态的光谱常数Table 2. Spectroscopic parameters for the
$\Omega$ states of SH– anion.$\Omega$ state Re/Å $\omega_{\rm{e}}$/cm–1 $\omega_{\rm{e}}\chi_{\rm{e}}$/cm–1 Be/cm–1 De/eV Te/cm–1 RMS/cm–1 ${{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 1.3435 2618.53 44.58 9.5589 3.8575 0 4.0232 ${{\rm{a}}^3}{\Pi _2}$ 第一势阱 1.3466 2584.13 72.08 9.5151 0.9607 20247.58 0.0257 第二势阱 2.1011 779.62 136.27 3.9082 0.4429 27639.82 1.1521 ${{\rm{a}}^{3}}{\Pi _1}$ 第一势阱 1.3463 2588.54 69.87 9.5196 0.9665 20363.64 0.0537 第二势阱 2.1005 773.93 135.45 3.9105 0.4173 27802.87 1.0389 ${{\rm{a}}^3}{\Pi _{{0^ - }}}$ 第一势阱 1.3466 2583.83 70.94 9.5149 0.9589 20624.88 0.0203 第二势阱 2.1036 776.84 132.77 3.8990 0.398 27989.31 1.1617 ${{\rm{a}}^3}{\Pi _{{0^ + }}}$ 第一势阱 1.3466 2583.89 70.92 9.5149 0.9594 20625.01 0.0195 第二势阱 2.1012 780.04 136.69 3.9079 0.4536 27999.08 1.3153 ${{\rm{A}}^1}{\Pi _1}$ 第一势阱 1.3444 2621.70 61.52 9.5464 1.2006 20924.71 0.0392 第二势阱 2.2449 422.69 37.82 3.4237 0.1026 30306.30 0.2834
DownLoad: CSV
表 3 SH–阴离子的辐射速率(单位为s–1)、弗兰克-康登因子和自发辐射寿命(单位为s)
Table 3. Emission rates
${A_{\nu ' \nu '' }}$ (unit of s–1), Franck-Condon factors${f_{\nu ' \nu '' }}$ and spontaneous radiative lifetimes$\tau $ (unit of s) of SH– anion.Transition A00 A01 A02 A03 A0 f00 f01 f02 f03 $\tau $ = 1/A0 A10 A11 A12 A13 f10 f11 f12 f13 ${\operatorname{a} ^3}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 677122 2184.69 25.3676 2.8984 679335 0.9990 0.0009 3.38 × 10–5 3.46 × 10–6 1.472 × 10–6 15577.8 561038 4025.17 35.1337 0.0010 0.9931 0.0054 0.0004 ${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 5310820 33.9404 30.5746 0.1736 5310885 0.9999 0.0001 2.18 × 10–6 1.07 × 10–8 1.883 × 10–7 2970.05 5262790 1089.41 217.62 0.0006 0.9992 0.0002 4.13 × 10–5 ${{\rm{a}}^3}{\Pi _{{0^ + }}} \leftrightarrow {{\rm{X}}^1}\Sigma _{0^ + }^ + $ 2229.24 98.3384 0.2456 0.0126 2327.84 0.9989 0.0011 3.82 × 10–5 3.53 × 10–6 4.295 × 10–4 102.87 2852.21 284.48 3.3484 0.0317 0.8795 0.0877 0.0010
DownLoad: CSV
-
[1] Shuman E S, Barry J F, DeMille D 2010 Nature 467 820
Google Scholar
[2] Zhelyazkova V, Cournol A, Wall T E, Matsushima A, Hudson J J, Hinds E A, Tarbutt M R, Sauer B E 2014 Phys. Rev. A 89 053416
Google Scholar
[3] Hummon M T, Yeo M, Stuhl B K, Collopy A L, Xia Y, Ye J 2013 Phys. Rev. Lett. 110
Google Scholar
[4] 张云光, 张华, 窦戈, 徐建刚 2017 66 233101
Google Scholar
Zhang Y G, Zhang H, Dou G, Xu J G 2017 Acta Phys. Sin. 66 233101
Google Scholar
[5] Gao Y, Gao T 2014 Phys. Rev. A 90 052506
Google Scholar
[6] Wan M, Shao J, Huang D, Jin C, Yu Y, Wang F 2015 Phys. Chem. Chem. Phys. 17 26731
Google Scholar
[7] Wan M, Shao J, Gao Y, Huang D, Yang J, Cao Q, Jin C, Wang F 2015 J. Chem. Phys. 143 024302
Google Scholar
[8] Gao Y, Gao T 2015 Phys. Chem. Chem. Phys. 17 10830
Google Scholar
[9] 李亚超, 孟腾飞, 李传亮等 2017 66 163101
Google Scholar
Li Y C, Meng T F, Li C L, et al. 2017 Acta Phys. Sin. 66 163101
Google Scholar
[10] Zhang Q, Yang C, Wang M, Ma X, Liu W 2017 Spectrochim. Acta, Part A 182 130
Google Scholar
[11] Zhang Q, Yang C, Wang M, Ma X, Liu W 2017 Spectrochim. Acta, Part A 185 365
Google Scholar
[12] Wan M, Huang D, Yu Y, Zhang Y 2017 Phys. Chem. Chem. Phys. 19 27360
Google Scholar
[13] Steiner B 1968 J. Chem. Phys. 49 5097
Google Scholar
[14] Breyer F, Frey P, Hotop H 1981 Z. Phys. 300 7
Google Scholar
[15] Janousek B K, Brauman J I 1981 Phys. Rev. A 23 1673
Google Scholar
[16] Cade P 1967 J. Chem. Phys. 47 2390
Google Scholar
[17] Rosmus P, Meyer W 1978 J. Chem. Phys. 69 2745
Google Scholar
[18] Senekowitsch J, Werner H J, Rosmus P, Reinsch E A, Oneil S V 1985 J. Chem. Phys. 83 4661
Google Scholar
[19] Vamhindi B S D R, Nsangou M 2016 Mol. Phys. 114 2204
Google Scholar
[20] Werner H J, Knowles P J 1988 J. Chem. Phys. 89 5803
Google Scholar
[21] Knowles P J, Werner H J 1988 Chem. Phys. Lett. 145 514
Google Scholar
[22] Langhoff S R, Davidson E R 1974 Int. J. Quantum Chem. 8 61
Google Scholar
[23] Knowles P J, Werner H J 1985 J. Chem. Phys. 82 5053
Google Scholar
[24] Knowles P J, Werner H J 1985 Chem. Phys. Lett. 115 259
Google Scholar
[25] Douglas M, Kroll N M 1974 Ann. Phys. 82 89
Google Scholar
[26] Hess B A 1986 Phys. Rev. A 33 3742
Google Scholar
[27] Berning A, Schweizer M, Werner H J, Knowles P J, Palmieri P 2000 Mol. Phys. 98 1823
Google Scholar
[28] Werner H J, Knowles P J, Lindh R, et al. MOLPRO, version 2010.1, a package of ab initio programs, 2010, see http://www.molpro.net [2018-11-15]
[29] Peterson K A, Dunning Jr T H 2002 J. Chem. Phys. 117 10548
Google Scholar
[30] Dunning Jr T H 1989 J. Chem. Phys. 90 1007
Google Scholar
[31] Murrell J N, Sorbie K S. 1974 J Chem. Soc., Faraday Trans. 70 1552
Google Scholar
[32] Le Roy R J Level 8.0: A Computer Program for Solving the Radial Schrödinger Equation for Bound and Quasibound Levels (Waterloo: University of Waterloo) Chemical Physics Research Report CP-663
[33] Lykke K R, Murray K K, Lineberger W C 1991 Rhys. Rev. A 43 6104
Google Scholar
[34] Hotop H, Lineberger W C 1985 J. Phys. Chem. Ref. Data 14 731
Google Scholar
[35] Moore C E 1971 Atomic Energy Levels (Vol. 1) (Washington, DC: National Bureau of Standards Publications) p181
[36] Cohen-Tannoudji C N 1998 Rev. Phys. Mod. 70 707
Google Scholar
[37] Kobayashi J, Aikawa K, Oasa K, Inouye S 2014 Phys. Rev. A 89 021401
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 7454
- PDF Downloads: 74
- Cited By: 0
