-
随着纳米科技以及半导体技术的迅猛发展, 光力诱导透明、快慢光和光存储以及其他在光力系统中发现的量子光学和非线性光学效应成为人们目前研究的热点. 本文将薄膜腔光力系统同被束缚在腔中的二能级冷原子系综相耦合, 通过直接在薄膜振子上引入弱辅助驱动场来研究该原子辅助光力系统中原子和相位对量子相干性质及其快慢光的调控. 经过分析发现, 通过改变辅助驱动场的强度可直接实现对光力诱导透明窗口深度的调控, 通过改变辅助场与探测场之间的相位差, 可实现输出的探测场在“吸收”、“透明”和“增益”之间相互转换, 进而对弱探测场进行动态调控实现光开关. 与此同时, 还发现系统的群延迟时间随相位差的改变呈周期性变化. 通过调节相位差及原子数, 不但可以改变群延迟时间, 还可实现快慢光之间的相互转换.In recent years, due to the rapid development of nano science and advanced semiconductor technology, one is able to observe more significant quantum optomechanical effects as optomechanical system turns smaller in size. Optomechanically induced transparency, fast and slow light, optical storage as well as other quantum optical and nonlinear optical effects have become the focus of research. On the other hand, the optomechanical systems coupled to other small subsystems (such as atoms, quantum dots, single electron transistors, etc.) also attract great attention in research. This is because the coupling system has not only provided more degrees of freedom for quantum manipulation, but also opened up more channels for classical and quantum information transfer. In this paper we study the optomechanically induced transparency and fast/slow light phase control in atom-assisted optomechanical cavity. Unlike the traditional systems, in this model the mechanical resonator is directly driven by a weak auxiliary driving field. We therefore find that with the change of amplitude ratio and phase difference between the auxiliary driving field and the probe field, the absorption and dispersion properties of the whole system and the group delay time vary accordingly. In the absence of auxiliary field, we observe the spectral features of the hybrid electromagnetically induced transparency and optomechanically induced transparency (OMIT) in an atom-cavity-oscillator tripartite optomechanical system. When there exists no phase difference between the auxiliary field and the probe field, we find that the membrane resonance absorption is enhanced with the increase of auxiliary field strength at resonance, causing the the optomechanically induced transparency to be suppressed, and therefore we can modify the amplitude of auxiliary field to control the depth of the OMIT window. When keeping amplitude ratio between the auxiliary field and the probe field unchanged, the modification of the phase difference between the auxiliary field and the probe field directly affects the we can not only realize the manipulation of OMIT window depth, but also control the transformation of tunable optical switch among "absorption", "transparent" and "gain" of the system. Therefore, through changing the phase of auxiliary field and probe field, we can not only realize the manipulation of OMIT window depth, but also control the transformation of tunable optical switch among "absorption" , "transparent" and "gain". In the meantime, we find that the system’s group delay time varies periodically with the change of phase difference. It is worth noting that by adjusting the phase difference and the atomic number, we can not only change the magnitude of the group delay, but also realize the conversion between slow light and fast light effect.
[1] Agarwal G S, Huang S M 2010 Phys. Rev. A 81 041803(R)
Google Scholar
[2] Safavi-Naeini A H, Mayer Alegre T P, Chan J, Eichenfield M, Winger M, Lin Q, Hill J T, Chang D E, Painter O 2011 Nature 472 69
Google Scholar
[3] Chang D E, Safavi-Naeini A H, Hafezi M, Painter O 2011 New J. Phys. 13 023003
Google Scholar
[4] Gu K H, Yan X B, Zhang Y, Fu C B, Liu Y M, Wang X, Wu J H 2015 Opt. Commun. 338 569
Google Scholar
[5] Chen B, Jiang C, Zhu K D 2011 Phys. Rev. A 83 055803
Google Scholar
[6] Jiang C, Liu H X, Cui Y S, Li X W, Chen G B, Chen B 2013 Opt. Express 21 12165
Google Scholar
[7] Tarhan D, Huang S, Müstecaplıoğlu Ö E 2013 Phys. Rev. A 87 013824
Google Scholar
[8] Fiore V, Yang Y, Kuzyk M C, Barbour R, Tian L, Wang H 2011 Phys. Rev. Lett. 107 133601
Google Scholar
[9] Tian L, Wang H L 2010 Phys. Rev. A 82 053806
Google Scholar
[10] Farman F, Bahrampour A R 2015 Phys. Rev. A 91 033828
Google Scholar
[11] McGee S A, Meiser D, Regal C A, Lehnert K W, Holland M J 2013 Phys. Rev. A 87 053818
Google Scholar
[12] Qu K, Agarwal G S 2013 Phys. Rev. A 87 031802(R)
Google Scholar
[13] Yan X B, Cui C L, Gu K H, Tian X D, Fu C B, Wu J H 2014 Opt. Express 22 4886
Google Scholar
[14] Barzanjeh S, Naderi M H, Soltanolkotabi M 2011 Phys. Rev. A 84 023803
Google Scholar
[15] Chan J, Alegr T P M, Safavi-Naeini A H, Hill J F, Krause A, Gröblacher S, Aspelmeyer M, Painter O 2011 Nature 478 89
Google Scholar
[16] Rabl P, Genes C, Hammerer K, Aspelmeyer M 2009 Phys. Rev. A 80 063819
Google Scholar
[17] Mari A, Eisert J 2009 Phys. Rev. Lett. 103 213603
Google Scholar
[18] Gu W J, Li G X 2013 Phys. Rev. A 88 013835
Google Scholar
[19] Mancini S, Giovannetti V, Vitali D, Tombesi P 2002 Phys. Rev. Lett. 88 120401
Google Scholar
[20] Hartmann M J, Plenio M B 2008 Phys. Rev. Lett. 101 200503
Google Scholar
[21] Mazzola L, Paternostro M 2011 Sci. Rep. 1 199
Google Scholar
[22] Yan X B 2017 Phys. Rev. A 96 053831
Google Scholar
[23] 张秀龙, 鲍倩倩, 杨明珠, 田雪松 2018 67 104203
Google Scholar
Zhang X L, Bao Q Q, Yang M Z, Tian X S 2018 Acta Phys. Sin. 67 104203
Google Scholar
[24] Stannigel K, Rabl P, Sorensen A S, Zoller P, Lukin M D 2010 Phys. Rev. Lett. 105 220501
Google Scholar
[25] Li J J, Zhu K D 2011 J. Appl. Phys. 110 114308
Google Scholar
[26] Agarwal G S, Huang S M 2014 New J. Phys. 16 033023
Google Scholar
[27] 刘欢, 曹士英, 孟飞, 林百科, 方占军 2015 64 094204
Google Scholar
Liu H, Cao S Y, Meng F, Lin B K, Fang Z J 2015 Acta Phys. Sin. 64 094204
Google Scholar
[28] Chang Y, Shi T, Liu Y X, Sun C P, Nori F 2011 Phys. Rev. A 83 063826
Google Scholar
[29] Fu C B, Yan X B, Gu K H, Cui C L, Wu J H, Fu T D 2013 Phys. Rev. A 87 053841
Google Scholar
[30] 韩明, 谷开慧, 刘一谋, 张岩, 王晓畅, 田雪冬, 付长宝, 崔淬砺 2014 63 094206
Google Scholar
Han M, Gu K H, Liu Y M, Zhang Y, Wang X C, Tian X D, Fu C B, Cui C L 2014 Acta Phys. Sin. 63 094206
Google Scholar
[31] Yan D, Wang Z H, Ren C N, Gao H, Li Y, Wu J H 2015 Phys. Rev. A 91 023813
Google Scholar
[32] He Q Y, Ficek Z 2014 Phys. Rev. A 89 022332
Google Scholar
[33] Genes C, Vitali D, Tombesi P 2008 Phys. Rev. A 77 050307
Google Scholar
[34] Genes C, Ritsch H, Drewsen M 2009 Phys. Rev. A 80 061803
Google Scholar
[35] Yi Z, Li G X, Wu S P, Yang Y P 2014 Opt. Express 22 20060
Google Scholar
[36] Walls D F, Milburn G J 1944 Quantum Optics (Berlin: Springer) p296
-
图 1 由单模FP腔以及束缚在其中的N个全同二能级87Rb冷原子系综和中间由弱辅助驱动场
${\varepsilon _{\rm{f}}}$ 驱动的振动频率为${\omega _{\rm{m}}}$ 的薄膜振子构成的光力学系统, 该系统的探测场和驱动场分别为${\varepsilon _{\rm{p}}}$ 和${\varepsilon _{\rm{d}}}$ Fig. 1. Schematic diagram of an optomechanical cavity containing N identical two-level cold 87Rb atoms with two fixed-end mirrors of equal reflectivity, which is driven by a strong coupling field
${\varepsilon _{\rm{d}}}$ , a weak auxiliary drive field${\varepsilon _{\rm{f}}}$ and probed by a weak field${\varepsilon _{\rm{p}}}$ .
图 2
$\operatorname{Re} ({\varepsilon _{\rm{T}}})$ (黑色实线)和${\rm{Im}}({\varepsilon _{\rm{T}}})$ (红色虚线)随频率失谐$\delta /{\omega _{\rm{m}}}$ 的变化曲线 (a)$Y = 0$ ;$\varPhi = 0$ ; (b)$Y = 0.05$ ;$\varPhi = 0$ ; (c)$Y = 0.2$ ;$\varPhi = 0$ ; 其他参数值见文中第4部分Fig. 2. The real (black line) and the imaginary (red dotted line) parts of
${\varepsilon _{\rm{T}}}$ as a function of$\delta /{\omega _{\rm{m}}}$ with (a)$Y = 0$ ;$\varPhi = 0$ ; (b)$Y = 0.05$ ;$\varPhi = 0$ ; (c)$Y = 0.2$ ;$\varPhi = 0$ . Relevant parameters are the same as those in Sec. 4.
图 3
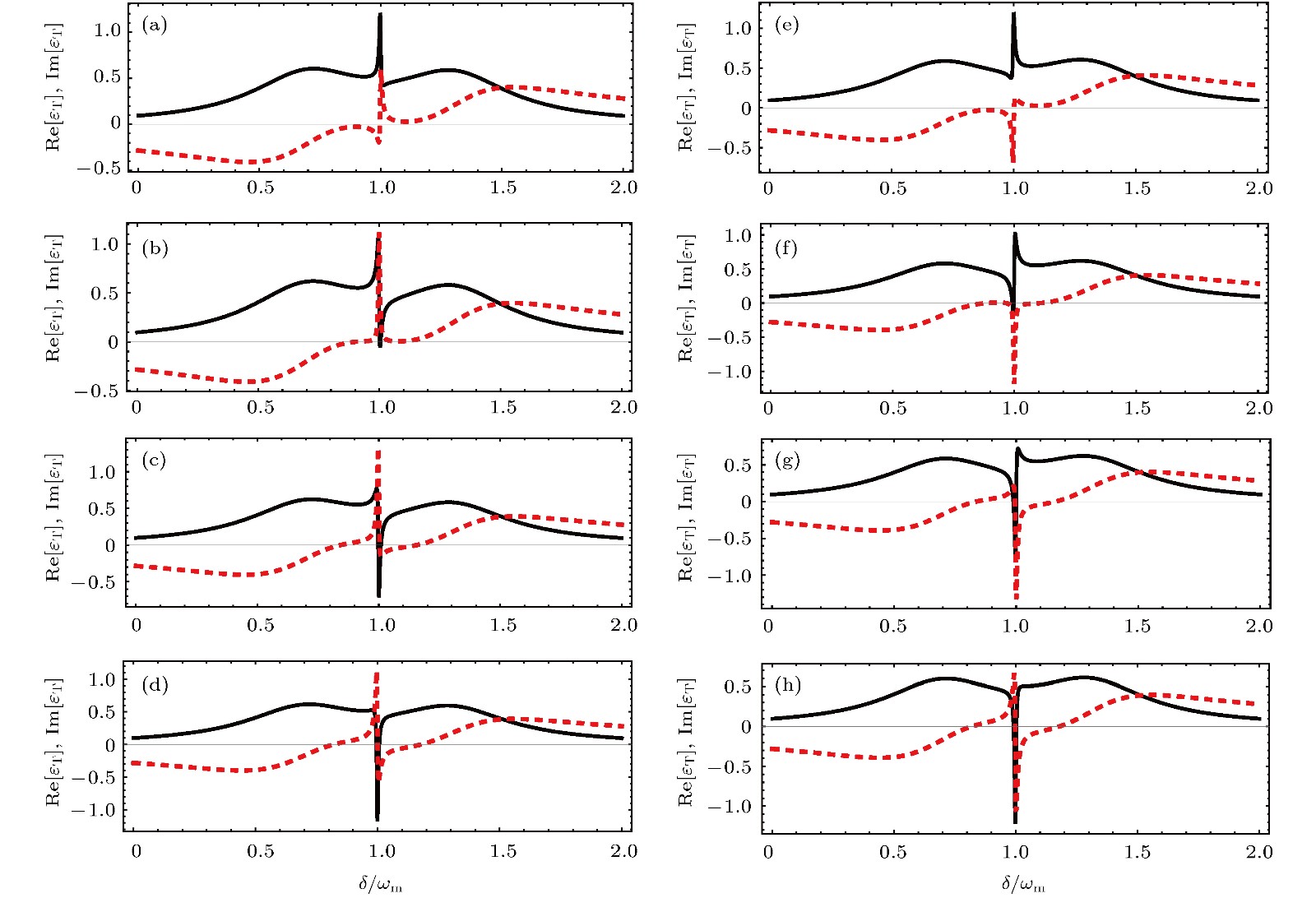
$Y = 0.2$ 时$\operatorname{Re} ({\varepsilon _{\rm{T}}})$ (黑色实线)和${\rm{Im}}({\varepsilon _{\rm{T}}})$ (红色虚线)随频率失谐$\delta /{\omega _{\rm{m}}}$ 的变化曲线 (a)$\varPhi = 0$ ; (b)$\varPhi = {\text{π}}/4$ ; (c)$\varPhi = {\text{π}}/2$ ; (d)$\varPhi = 3{\text{π}}/4$ ; (e)$\varPhi = {\text{π}}$ ; (f)$\varPhi = 5{\text{π}} /4$ ; (g)$\varPhi = 6{\text{π}}/4$ ; (h)$\varPhi = 7{\text{π}}/4$ ; 其他参数值见文中第4部分Fig. 3. The real (black line) and the imaginary (red dotted line) parts of
${\varepsilon _{\rm{T}}}$ as a function of$\delta /{\omega _{\rm{m}}}$ with$Y = 0.2$ : (a)$\varPhi = 0$ ; (b)$\varPhi = {\text{π}}/4$ ; (c)$\varPhi = {\text{π}}/2$ ; (d)$\varPhi = 3{\text{π}}/4$ ; (e)$\varPhi = {\text{π}} $ ; (f)$\varPhi = 5{\text{π}}/4$ ; (g)$\varPhi = 6{\text{π}}/4$ ; (h)$\varPhi = 7{\text{π}}/4$ . Other parameters are the same as those in Sec. 4.
图 4
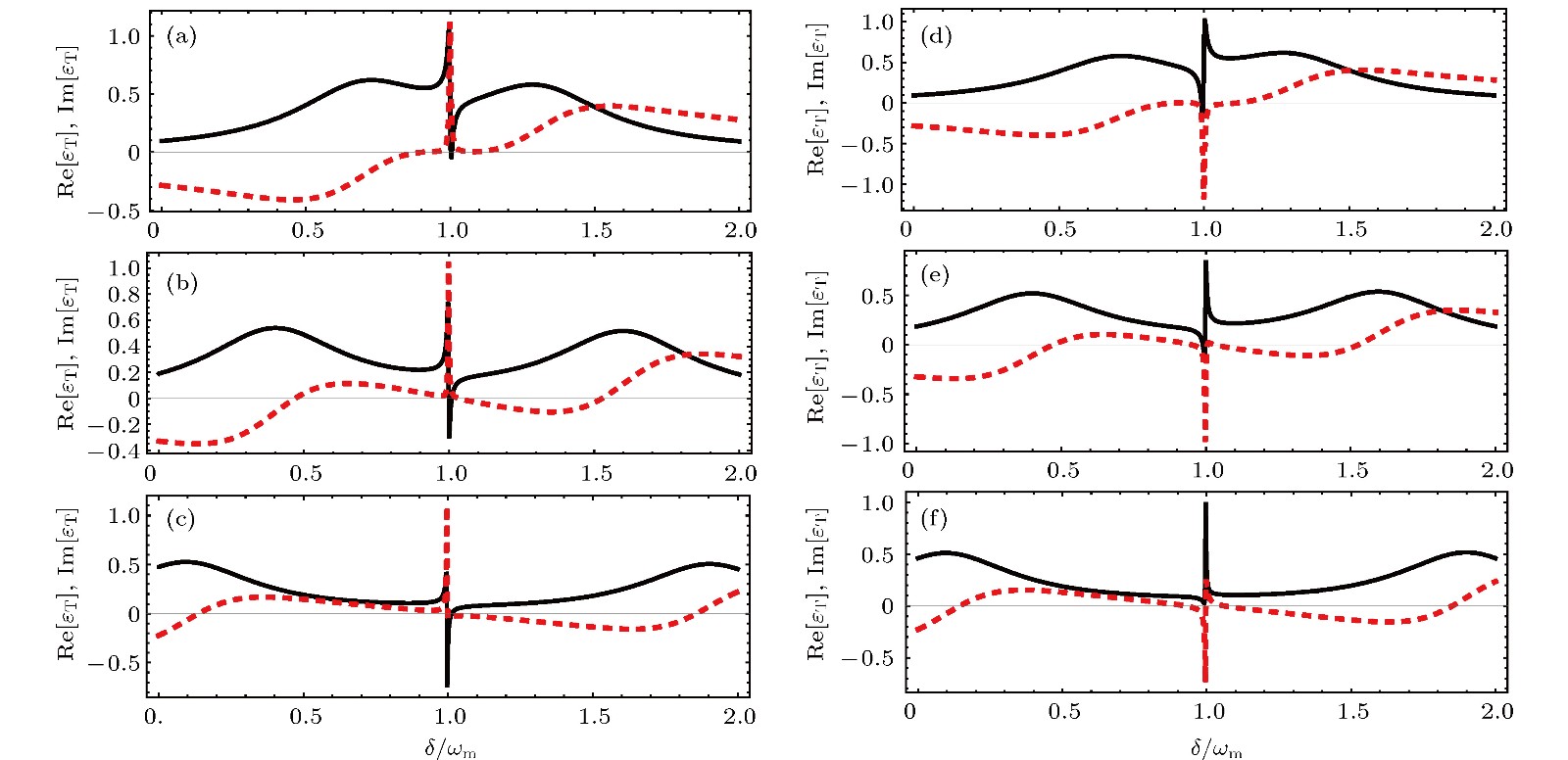
$Y = 0.2$ 时$\operatorname{Re} ({\varepsilon _{\rm{T}}})$ (黑色实线)和${\rm{Im}}({\varepsilon _{\rm{T}}})$ (红色虚线)随频率失谐$\delta /{\omega _{\rm{m}}}$ 的变化曲线 (a)$\varPhi = {\text{π}}/4$ ,$g\sqrt N = 3 \times 2{\text{π}}$ MHz; (b)$\varPhi = {\text{π}}/4$ ,$g\sqrt N = 6 \times 2{\text{π}}$ MHz; (c)$\varPhi = {\text{π}}/4$ ,$g\sqrt N = 9 \times 2{\text{π}}$ MHz; (d)$\varPhi = 6{\text{π}}/4$ ,$g\sqrt N = 3 \times 2{\text{π}}$ MHz; (e)$\varPhi = 6{\text{π}}/4$ ,$g\sqrt N = 6 \times 2{\text{π}}$ MHz; (f)$\varPhi = 6{\text{π}}/4$ ,$g\sqrt N = 9 \times 2{\text{π}}$ MHz; 其他参数值见文中第4部分Fig. 4. The real (black line) and the imaginary (red dotted line) parts of
${\varepsilon _{\rm{T}}}$ as a function of$\delta /{\omega _{\rm m}}$ with$Y = 0.2$ : (a)$\varPhi = {\text{π}}/4$ ,$g\sqrt N = 3 \times 2{\text{π}}$ MHz; (b)$\varPhi = {\text{π}}/4$ ,$g\sqrt N = 6 \times 2{\text{π}}$ MHz; (c)$\varPhi = {\text{π}}/4$ ,$g\sqrt N = 9 \times 2{\text{π}}$ MHz; (d)$\varPhi = 6{\text{π}}/4$ ,$g\sqrt N = 3 \times 2{\text{π}}$ MHz; (e)$\varPhi = 6{\text{π}}/4$ ,$g\sqrt N = 6 \times {{2{\text{π}} }}$ MHz; (f)$\varPhi = 6{\text{π}}/4$ ,$g\sqrt N = 9 \times {{2{\text{π}} }}$ MHz. Other parameters are the same as those in Sec. 4.
图 5
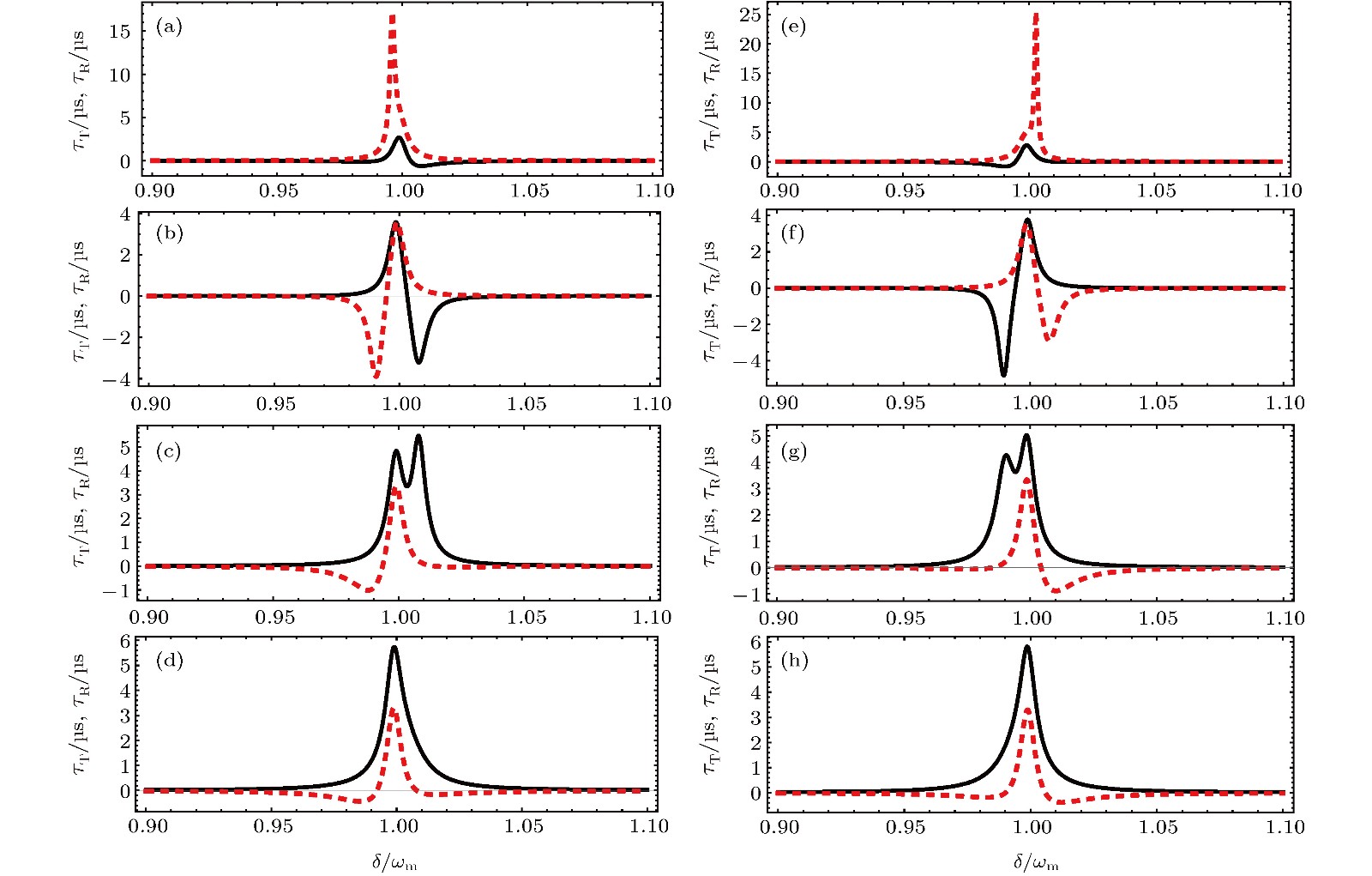
${\tau _{\rm{T}}}$ (黑色实线)和${\tau _{\rm{R}}}$ (红色虚线)随频率失谐$\delta /{\omega _{\rm{m}}}$ 的变化曲线: (a)$\varPhi = 0$ ; (b)$\varPhi = {\text{π}}/4$ ; (c)$\varPhi = {\text{π}}/2$ ; (d)$\varPhi = 3{\text{π}}/4$ ; (e)$\varPhi = {\text{π}}$ ; (f)$\varPhi = 5{\text{π}} /4$ ; (g)$\varPhi = 6{\text{π}}/4$ ; (h)$\varPhi = 7{{{\text{π}} }}/4$ ; 其他参数取值同图3Fig. 5. The
${\tau _{\rm{T}}}$ (black line) and the${\tau _{\rm{R}}}$ (red dotted line) as a function of$\delta /{\omega _{\rm{m}}}$ with (a)$\varPhi = 0$ ; (b)$\varPhi = {\text{π}}/4$ ; (c)$\varPhi = {\text{π}}/2$ ; (d)$\varPhi = 3{\text{π}}/4$ ; (e)$\varPhi = {\text{π}}$ ; (f)$\varPhi = 5{\text{π}}/4$ ; (g)$\varPhi = {{6{\text{π}} /}}4$ ; (h)$\varPhi = 7{\text{π}}/4$ . Other parameters are the same as those in Fig.3.
图 6
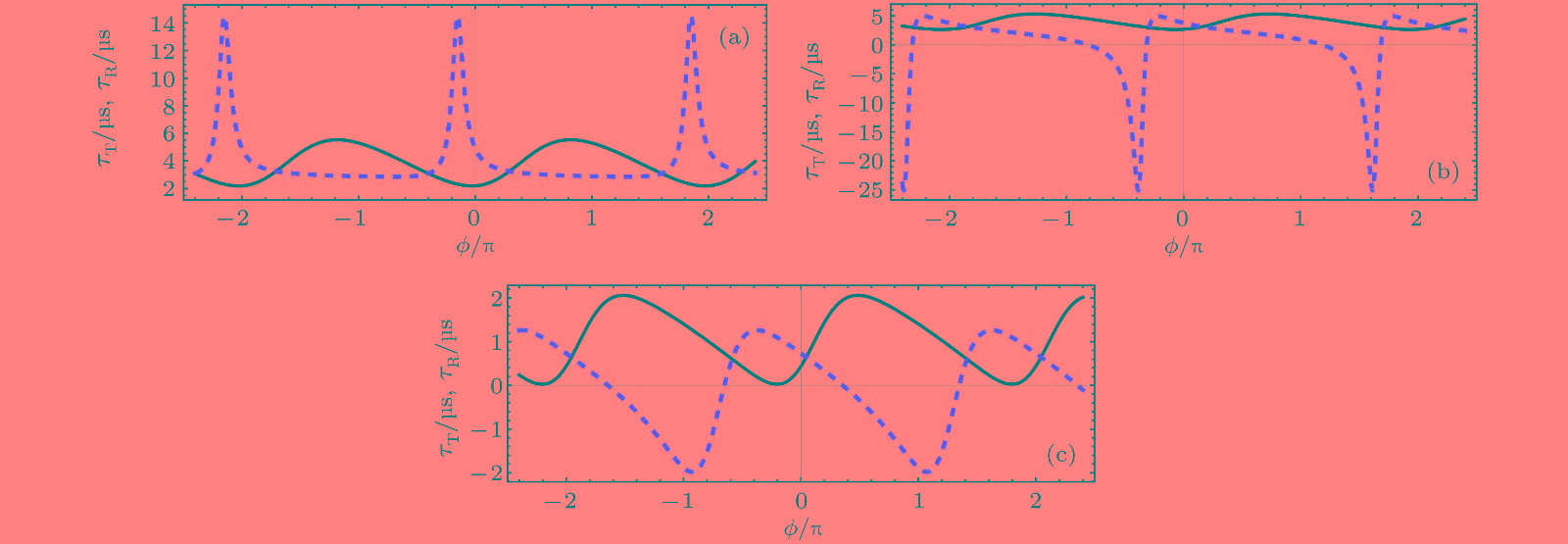
$\delta = {\omega _{\rm{m}}}$ 时${\tau _{\rm{T}}}$ (黑色实线)和${\tau _{\rm{R}}}$ (红色虚线)随相位差$\varPhi /{\text{π}}$ 和振幅比$Y$ 的变化曲线: (a)$Y = 0.2$ ,$g\sqrt N = 3 \times 2{\text{π}}$ MHz; (b)$Y = 0.2$ ,$g\sqrt N = 6 \times 2{\text{π}}$ MHz; (c)$Y = 0.2$ ,$g\sqrt N = 9 \times 2{\text{π}}$ MHz; 其他参数取值见文中第4部分Fig. 6. The
${\tau _{\rm{T}}}$ (black line) and the${\tau _{\rm{R}}}$ (red dotted line) as a function of$\varPhi /{\text{π}}$ and Y with$\delta = {\omega _{\rm{m}}}$ : (a)$Y = 0.2$ ,$g\sqrt N = 3 \times 2{\text{π}}$ MHz; (b)$Y = 0.2$ ,$g\sqrt N = 6 \times 2{\text{π}}$ MHz; (c)$Y = 0.2$ ,$g\sqrt N = 9 \times 2{\text{π}}$ MHz. Other parameters are the same as those in Sec. IV. -
[1] Agarwal G S, Huang S M 2010 Phys. Rev. A 81 041803(R)
Google Scholar
[2] Safavi-Naeini A H, Mayer Alegre T P, Chan J, Eichenfield M, Winger M, Lin Q, Hill J T, Chang D E, Painter O 2011 Nature 472 69
Google Scholar
[3] Chang D E, Safavi-Naeini A H, Hafezi M, Painter O 2011 New J. Phys. 13 023003
Google Scholar
[4] Gu K H, Yan X B, Zhang Y, Fu C B, Liu Y M, Wang X, Wu J H 2015 Opt. Commun. 338 569
Google Scholar
[5] Chen B, Jiang C, Zhu K D 2011 Phys. Rev. A 83 055803
Google Scholar
[6] Jiang C, Liu H X, Cui Y S, Li X W, Chen G B, Chen B 2013 Opt. Express 21 12165
Google Scholar
[7] Tarhan D, Huang S, Müstecaplıoğlu Ö E 2013 Phys. Rev. A 87 013824
Google Scholar
[8] Fiore V, Yang Y, Kuzyk M C, Barbour R, Tian L, Wang H 2011 Phys. Rev. Lett. 107 133601
Google Scholar
[9] Tian L, Wang H L 2010 Phys. Rev. A 82 053806
Google Scholar
[10] Farman F, Bahrampour A R 2015 Phys. Rev. A 91 033828
Google Scholar
[11] McGee S A, Meiser D, Regal C A, Lehnert K W, Holland M J 2013 Phys. Rev. A 87 053818
Google Scholar
[12] Qu K, Agarwal G S 2013 Phys. Rev. A 87 031802(R)
Google Scholar
[13] Yan X B, Cui C L, Gu K H, Tian X D, Fu C B, Wu J H 2014 Opt. Express 22 4886
Google Scholar
[14] Barzanjeh S, Naderi M H, Soltanolkotabi M 2011 Phys. Rev. A 84 023803
Google Scholar
[15] Chan J, Alegr T P M, Safavi-Naeini A H, Hill J F, Krause A, Gröblacher S, Aspelmeyer M, Painter O 2011 Nature 478 89
Google Scholar
[16] Rabl P, Genes C, Hammerer K, Aspelmeyer M 2009 Phys. Rev. A 80 063819
Google Scholar
[17] Mari A, Eisert J 2009 Phys. Rev. Lett. 103 213603
Google Scholar
[18] Gu W J, Li G X 2013 Phys. Rev. A 88 013835
Google Scholar
[19] Mancini S, Giovannetti V, Vitali D, Tombesi P 2002 Phys. Rev. Lett. 88 120401
Google Scholar
[20] Hartmann M J, Plenio M B 2008 Phys. Rev. Lett. 101 200503
Google Scholar
[21] Mazzola L, Paternostro M 2011 Sci. Rep. 1 199
Google Scholar
[22] Yan X B 2017 Phys. Rev. A 96 053831
Google Scholar
[23] 张秀龙, 鲍倩倩, 杨明珠, 田雪松 2018 67 104203
Google Scholar
Zhang X L, Bao Q Q, Yang M Z, Tian X S 2018 Acta Phys. Sin. 67 104203
Google Scholar
[24] Stannigel K, Rabl P, Sorensen A S, Zoller P, Lukin M D 2010 Phys. Rev. Lett. 105 220501
Google Scholar
[25] Li J J, Zhu K D 2011 J. Appl. Phys. 110 114308
Google Scholar
[26] Agarwal G S, Huang S M 2014 New J. Phys. 16 033023
Google Scholar
[27] 刘欢, 曹士英, 孟飞, 林百科, 方占军 2015 64 094204
Google Scholar
Liu H, Cao S Y, Meng F, Lin B K, Fang Z J 2015 Acta Phys. Sin. 64 094204
Google Scholar
[28] Chang Y, Shi T, Liu Y X, Sun C P, Nori F 2011 Phys. Rev. A 83 063826
Google Scholar
[29] Fu C B, Yan X B, Gu K H, Cui C L, Wu J H, Fu T D 2013 Phys. Rev. A 87 053841
Google Scholar
[30] 韩明, 谷开慧, 刘一谋, 张岩, 王晓畅, 田雪冬, 付长宝, 崔淬砺 2014 63 094206
Google Scholar
Han M, Gu K H, Liu Y M, Zhang Y, Wang X C, Tian X D, Fu C B, Cui C L 2014 Acta Phys. Sin. 63 094206
Google Scholar
[31] Yan D, Wang Z H, Ren C N, Gao H, Li Y, Wu J H 2015 Phys. Rev. A 91 023813
Google Scholar
[32] He Q Y, Ficek Z 2014 Phys. Rev. A 89 022332
Google Scholar
[33] Genes C, Vitali D, Tombesi P 2008 Phys. Rev. A 77 050307
Google Scholar
[34] Genes C, Ritsch H, Drewsen M 2009 Phys. Rev. A 80 061803
Google Scholar
[35] Yi Z, Li G X, Wu S P, Yang Y P 2014 Opt. Express 22 20060
Google Scholar
[36] Walls D F, Milburn G J 1944 Quantum Optics (Berlin: Springer) p296
下载:
计量
- 文章访问数: 8395
- PDF下载量: 94
- 被引次数: 0
