-
Rydberg atoms have attracted considerable attention due to their several singular properties, such as strong long-range interactions, extremely long lifetimes, and very large polarizability. These characteristics make Rydberg atoms a good candidates for cavity quantum electrodynamics, quantum information, and many-body physics. Recently, the study of optomechanics has become a rapidly developing field due to its important applications in cooling of mechanical resonators, implementing precision measurements, slowing light, and preparing quantum entanglement. Obviously, optomechanical systems pave the way for quantum information processing and quantum communication. Specially, there is significant interest in quantum optomechanics due to its high compatibility that can be combined, to build hybrid systems for certain purposes, with the ultracold atoms, a superconducting single electron transistor, a magnetostrictive actuation, a charged oscillator resonator, etc. In this work, we investigate the optomechanically induced transparency (OMIT) and the resulting effect of slow light in a hybrid system composed of a Rydberg atomic ensemble embedded inside a simple optomechanical cavity. As a typical effect of destructive quantum interference, OMIT is widely used in quantum optics and quantum information processing. Based on the Rydberg blockade effect, a Rydberg atomic ensemble in the same blockade region embedded inside an optomechanical cavity can be regarded as a superatom that contains only a single Rydberg excitation. Therefore, the problem of exponentially increasing system size with the number of atoms increasing can be circumvented easily. The hybrid system becomes a coupling between a Rydberg superatom and an optomechanical cavity and the coupling strength is enhanced by a factor of square root of the number of atoms in the ensemble. In this system, the perfect OMIT, namely, an ideal OMIT dip with a very narrow window, can be attained when an effect of non-rotating wave approximation (NRWA) is considered. Further, we demonstrate that the term of NRWA plays a key important role in achieving perfect OMIT by comparing the optomechanical spectra obtained with and without NRWA effects. Our results show that in the resolved sideband regime the higher the quality factor of cavity is, the stronger the slow light effect becomes in the window of the perfect OMIT. Particularly, in achieving the ultraslow light, the long lifetime of the Rydberg atom shows its superiority.
-
Keywords:
- optomechanically induced transparency /
- slow light /
- Rydberg atom /
- dipole blockade
[1] Kippenberg T J, Vahala K J 2008 Science 321 1172
Google Scholar
[2] Aspelmeyer M, Gröblacher S, Hammerer K 2010 J. Opt. Soc. Am. B 27 A189
Google Scholar
[3] Aspelmeyer M, Meystre P, Schwab K 2012 Phys. Today 65 29
[4] Xiong H, Si L G, Zheng A S 2012 Phys. Rev. A 86 013815
Google Scholar
[5] Lü X Y, Wu Y, Johansson J R, Jing H, Zhang J, Nori F 2015 Phys. Rev. Lett. 114 253601
Google Scholar
[6] Lü X Y, Wu Y, Johansson J R, Jing H, Zhang J, Nori F 2015 Phys. Rev. Lett. 114 093602
Google Scholar
[7] Grudinin I S, Lee H, Painter O, Vahala K J 2010 Phys. Rev. Lett. 104 083901
Google Scholar
[8] Mahboob I, Nishiguchi K, Fujiwara A, Yamaguchi H 2013 Phys. Rev. Lett. 110 127202
Google Scholar
[9] Jing H, Özdemir S K, Lü X Y, Zhang J, Yang L, Nori F 2014 Phys. Rev. Lett. 113 053604
Google Scholar
[10] Brooks D W C, Botter T, Schreppler S, Purdy T P, Brahms N, Stamper-Kurn D M 2012 Nature 488 476
Google Scholar
[11] LaHaye M D, Camarota O B B, Schwab K C 2004 Science 304 74
Google Scholar
[12] Ekinci K L, Yang Y T, Roukes M L 2004 J. Appl. Phys. 95 2682
Google Scholar
[13] Caves C M 1980 Phys. Rev. Lett. 45 75
Google Scholar
[14] Gavartin E, Verlot P, Kippenberg T J 2012 Nat. Nanotechnol. 7 509
Google Scholar
[15] Chan J, Mayer Alegre T P, Safavi-Naeini A H, Hill J T, Krause A, Groblacher S, Aspelmeyer M, Painter O 2011 Nature 478 89
Google Scholar
[16] Aspelmeyer M, Kippenberg T J, Marquardt F 2014 Rev. Mod. Phys. 86 1391
Google Scholar
[17] Mancini S, Giovannetti V, Vitali D, Tombesi P 2002 Phys. Rev. Lett. 88 120401
Google Scholar
[18] Harris S E 1997 Phys. Today 50 36
[19] Fleichhauer M, Imamoglu A, Marangos J P 2005 Rev. Mod. Phys. 77 633
Google Scholar
[20] Agarwal G S, Huang S 2010 Phys. Rev. A 81 041803
Google Scholar
[21] Weis S, Rivière R, Deléglise S 2010 Science 330 1520
Google Scholar
[22] Safavi-Naeini A H, Mayer Alegre T P, Chan J, Eichenfield M, Winger M, Lin Q, Hill J T, Chang D E, Painter O 2011 Nature 472 69
Google Scholar
[23] Akram M J, Khan M M, Saif F 2015 Phys. Rev. A 92 023846
Google Scholar
[24] Yan X B 2020 Phys. Rev. A 101 043820
Google Scholar
[25] Ian H, Gong Z R, Liu Y 2008 Phys. Rev. A 78 013824
Google Scholar
[26] Genes C, Vitali D, Tombesi P 2008 Phys. Rev. A 77 050307
Google Scholar
[27] Akram M J, Ghafoor F, Saif F 2015 J. Phys. B At. Mol. Opt. Phys. 48 065502
Google Scholar
[28] Paternostro M, De Chiara G, Palma G M 2010 Phys. Rev. Lett. 104 243602
Google Scholar
[29] Jia W Z, Wang Z D 2013 Phys. Rev. A 88 063821
Google Scholar
[30] Lecocq F, Teufel J D, Aumentado J 2015 Nat. Phys. 11 635
Google Scholar
[31] Yan D, Wang Z H, Ren C N, Gao H, Li Y, Wu J H 2015 Phys. Rev. A 91 023813
Google Scholar
[32] Gallagher T F 1994 Rydberg Atoms (Cambridge: Cambridge University Press)
[33] Lukin M D, Fleischhauer M, Cote R, Duan L M, Jaksch D, Cirac J I, Zoller P 2001 Phys. Rev. Lett. 87 037901
Google Scholar
[34] Heidemann R, Raitzsch U, Bendkowsky V, Butscher B, Low R, Santos L, Pfau T 2007 Phys. Rev. Lett. 99 163601
Google Scholar
[35] Saffman M, Walker T, Molmer K 2010 Rev. Mod. Phys. 82 2313
Google Scholar
[36] Weimer H, Muller M, Lesanovsky I, Zoller P, Buchler H P 2010 Nat. Phys. 6 382
Google Scholar
[37] Saffman M, Walker T G 2002 Phys. Rev. A 66 065403
Google Scholar
[38] Fu C B, Yan X B, Gu K H 2013 Phys. Rev. A 87 053841
Google Scholar
[39] Yan D, Bai W J, Bai J N, Chen L, Han H Y, Wu J H 2022 Photonics 9 242
Google Scholar
[40] Marek T, Grigori E A, Boris A M, Dmitry S P 2020 Phys. Rev. A 101 051601
Google Scholar
[41] Khodas M, Pustilnik M, Kamenev A, Glazman L I 2007 Phys. Rev. Lett. 99 110405
Google Scholar
[42] Karla L, Jean-Sébastien B, Roberta C, Edmond O, Corinna K 2018 Phys. Rev. A 98 033605
Google Scholar
[43] Yan X B 2021 J. Phys. B: At. Mol. Opt. Phys. 54 035401
Google Scholar
[44] Walls D F, Milburn G J 1944 Quantum Optics (Berlin: Springer-Verlag) pp127−141
-
图 1 (a)典型的光力学微腔内部捕获里德伯原子系综, 并且这些原子都在同一个偶极阻塞区域. 右侧为二能级里德伯原子的能级结构, 两个里德伯原子间通过范德瓦耳斯势作用在一起. (b)同一阻塞区域的原子系综可以看作共享最多一个里德伯激发的超级原子, 因而系统可以退化为里德伯超级原子与光力学微腔的强关联系统. 右侧为二能级里德伯超级原子的能级结构图
Fig. 1. (a) Schematic diagram of a typical hybrid optomechanical system containing a Rydberg ensemble where all atoms are in the same blockade region. Right: Energy level diagram of a two-level Rydberg atom. Two Rydberg atoms couple strongly via van der Waals (vdW) potential. (b) The hybrid optomechanical system can be regarded as a typical optomechanical system coupled a Rydberg superatom sharing at most one Rydberg excitation. Right: Energy level diagram of a two-level Rydberg superatom.
图 2 (a)
${\rm Re} \left[ {{\varepsilon _{\text{T}}}} \right]$ 和${\rm Re} \left[ {\varepsilon _{\text{T}}'} \right]$ , (b)${\rm Im} \left[ {{\varepsilon _{\text{T}}}} \right]$ 和$ {\rm Im} \left[ {\varepsilon _{\text{T}}'} \right] $ 作为$ x/{\gamma _{\text{m}}} $ 的函数. 其中光力学参数为$ {\omega _{\text{m}}}/(2{\text{π )}} = 134{\text{ kHz}} $ ,$ \kappa = {\omega _{\text{m}}} $ ,$ Q = {10^4} $ ; 原子参数为$ n = {10^2} $ ,$ {\gamma _{\text{r}}}{\text{/(2\pi )}} = 0.02{\text{ MHz}} $ , 并保证完美光力透明条件$ \beta = {\beta _0} $ ; 黑色实线代表$ {\varepsilon _{\text{T}}} $ , 而红色短划线代表$ \varepsilon _{\text{T}}' $ Fig. 2. (a)
$ {\rm Re} \left[ {{\varepsilon _{\text{T}}}} \right] $ and$ {\rm Re} \left[ {\varepsilon _{\text{T}}'} \right] $ , (b)$ {\rm Im} \left[ {\varepsilon _{\text{T}}^{}} \right] $ and$ {\rm Im} \left[ {\varepsilon _{\text{T}}'} \right] $ as a function of$ x/{\gamma _{\text{m}}} $ with optomechanical parameters${\omega _{\text{m}}}{\text{/(2\pi )}} = $ $ 134{\text{ kHz}}$ ,$ \kappa = {\omega _{\text{m}}} $ ,$ Q = {10^4} $ ; atomic parameters$ n = {10^2} $ ,${\gamma _{\text{r}}}{\text{/(2\pi )}} = 0.02{\text{ MHz}}$ , and the condition of perfect OMIT$ \beta = {\beta _0} $ . Here, the black solid curve represents$ {\varepsilon _{\text{T}}} $ while the red dashed curve represents$ \varepsilon _{\text{T}}' $ .
图 3 (a)
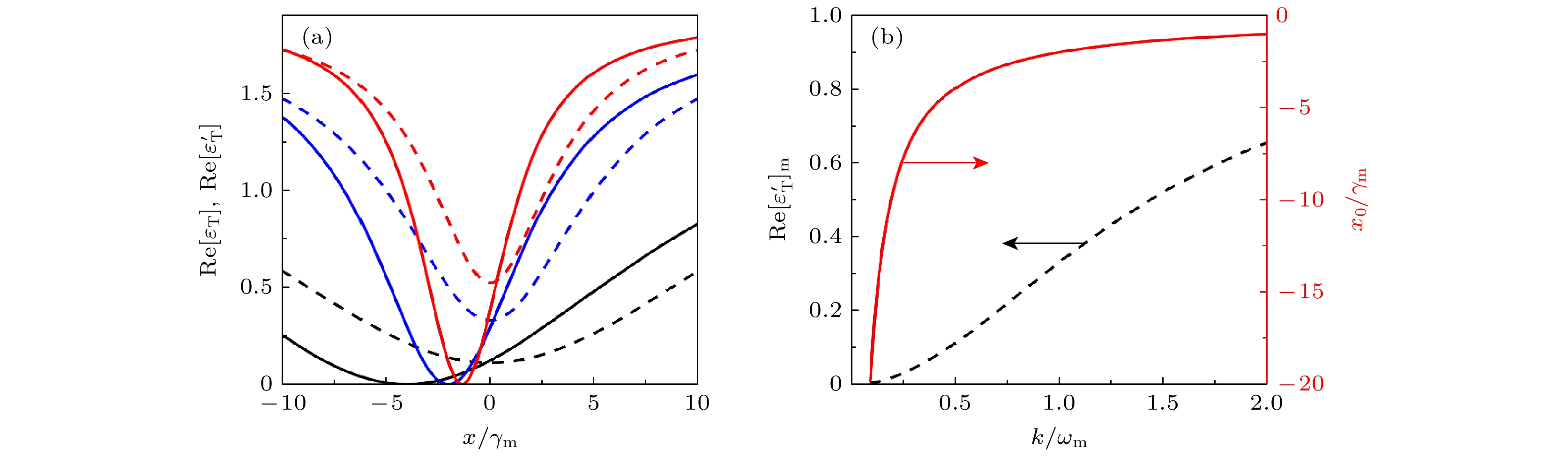
$ {\rm Re} \left[ {{\varepsilon _{\text{T}}}} \right] $ 和$ {\rm Re} \left[ {\varepsilon _{\text{T}}'} \right] $ 作为$ x/{\gamma _{\text{m}}} $ 的函数, 黑色、蓝色、红色曲线分别为$ \kappa /{\omega _{\text{m}}} = 0.5 $ ,$ \kappa /{\omega _{\text{m}}} = 1.0 $ 以及$ \kappa /{\omega _{\text{m}}} = 1.5 $ , 实线(短划线)代表$ {\varepsilon _{\text{T}}} $ ($ \varepsilon _{\text{T}}' $ ); (b)${\rm Re} {\left[ {\varepsilon _{\text{T}}'} \right]_{\text{m}}}$ 和$ {x_0}/{\gamma _m} $ 与$ \kappa /{\omega _m} $ 的关系函数, 因为完美OMIT窗口有$ {\rm Re} \left[ {{\varepsilon _{\text{T}}}} \right] = 0 $ , 所以${\rm Re} {\left[ {\varepsilon _{\text{T}}'} \right]_{\text{m}}} = $ $ \min \left\{ {{\rm Re} \left[ {\varepsilon _{\text{T}}'} \right]} \right\}$ 直接表示包含$ N $ 与不包含$ N $ 两种情况下窗口内吸收的差值, 其他参数同图2Fig. 3. (a)
$ {\rm Re} \left[ {{\varepsilon _{\text{T}}}} \right] $ and$ {\rm Re} \left[ {\varepsilon _{\text{T}}'} \right] $ as a function of$ x/{\gamma _{\text{m}}} $ with$ \kappa /{\omega _{\text{m}}} = 0.5 $ (black curve),$ \kappa /{\omega _{\text{m}}} = 1.0 $ (blue curve) and$ \kappa /{\omega _{\text{m}}} = 1.5 $ (red curve). The solid (dashed) curve represents$ {\varepsilon _{\text{T}}} $ ($ \varepsilon _{\text{T}}' $ ). (b)${\rm Re} {\left[ {\varepsilon _{\text{T}}'} \right]_{\text{m}}}$ and$ x/{\gamma _{\text{m}}} $ as a function of$ \kappa /{\omega _m} $ . Here,${\rm Re} {\left[ {\varepsilon _{\text{T}}'} \right]_{\text{m}}} = $ $ \min \left\{ {{\rm Re} \left[ {\varepsilon _{\text{T}}{'}} \right]} \right\}$ represents the difference of absorptions in the window with and without$ N $ due to$ {\rm Re} \left[ {{\varepsilon _{\text{T}}}} \right] $ = 0. Other parameters are the same as those in Fig. 2.
图 4 (a1)和(a2)
${\rm Re} {\left[ {\varepsilon _{\text{T}}'} \right]_{\text{m}}}$ (黑色短划线)和$ {x_0}/{\gamma _{\text{m}}} $ (红色实线)作为lgn的函数, (a1)和(a2)分别对应$ \kappa /{\omega _{\text{m}}} = 0.1 $ 和$ \kappa /{\omega _{\text{m}}} = 2.0 $ ; (b1)和(b2)${\rm Re} {\left[ {\varepsilon _{\text{T}}'} \right]_{\text{m}}}$ (黑色短划线)和$ {x_0}/{\gamma _{\text{m}}} $ (红色实线)作为$ {\gamma _{\text{r}}} $ 的函数, (b1)和(b2)分别对应$ \kappa /{\omega _{\text{m}}} = 0.1 $ 和$ \kappa /{\omega _{\text{m}}} = 2.0 $ , 其他参数同图2Fig. 4. (a1) and (a2)
${\rm Re} {\left[ {\varepsilon _{\text{T}}'} \right]_{\text{m}}}$ (black dashed curve) and$ {x_0}/{\gamma _{\text{m}}} $ (red solid curve) as a function of lgn, (a1) and (a2) correspond to$ \kappa /{\omega _{\text{m}}} = 0.1 $ and$ \kappa /{\omega _{\text{m}}} = 2.0 $ , respectively; (b1) and (b2)${\rm Re} {\left[ {\varepsilon _{\text{T}}'} \right]_{\text{m}}}$ (black dashed curve) and$ {x_0}/{\gamma _{\text{m}}} $ (red solid curve) as a function of$ {\gamma _{\text{r}}} $ . (b1) and (b2) correspond to$ \kappa /{\omega _{\text{m}}} = 0.1 $ and$ \kappa /{\omega _{\text{m}}} = 2.0 $ , respectively. Other parameters are the same as those in Fig. 2.
图 5
${\rm Re} \left[ {{\varepsilon _{\text{T}}}} \right]$ (黑色实线)、${\rm Im} \left[ {\varepsilon _{\text{T}}^{}} \right]$ (蓝色短划线)以及$ \tau $ (红色点线)作为$ x/{\gamma _{\text{m}}} $ 的函数, 绿色竖线给出完美光力诱导透明坐标$ {x_0} $ , 参数同图2Fig. 5.
${\rm Re} \left[ {{\varepsilon _{\text{T}}}} \right]$ (black solid curve),${\rm Im} \left[ {\varepsilon _{\text{T}}^{}} \right]$ (blue dashed curve), and$ \tau $ (red dotted curve) as a function of$ x/{\gamma _{\text{m}}} $ . The green vertical line denotes$ {x_0} $ of perfect OMIT, all parameters are the same as those in Fig. 2.
图 6 (a)
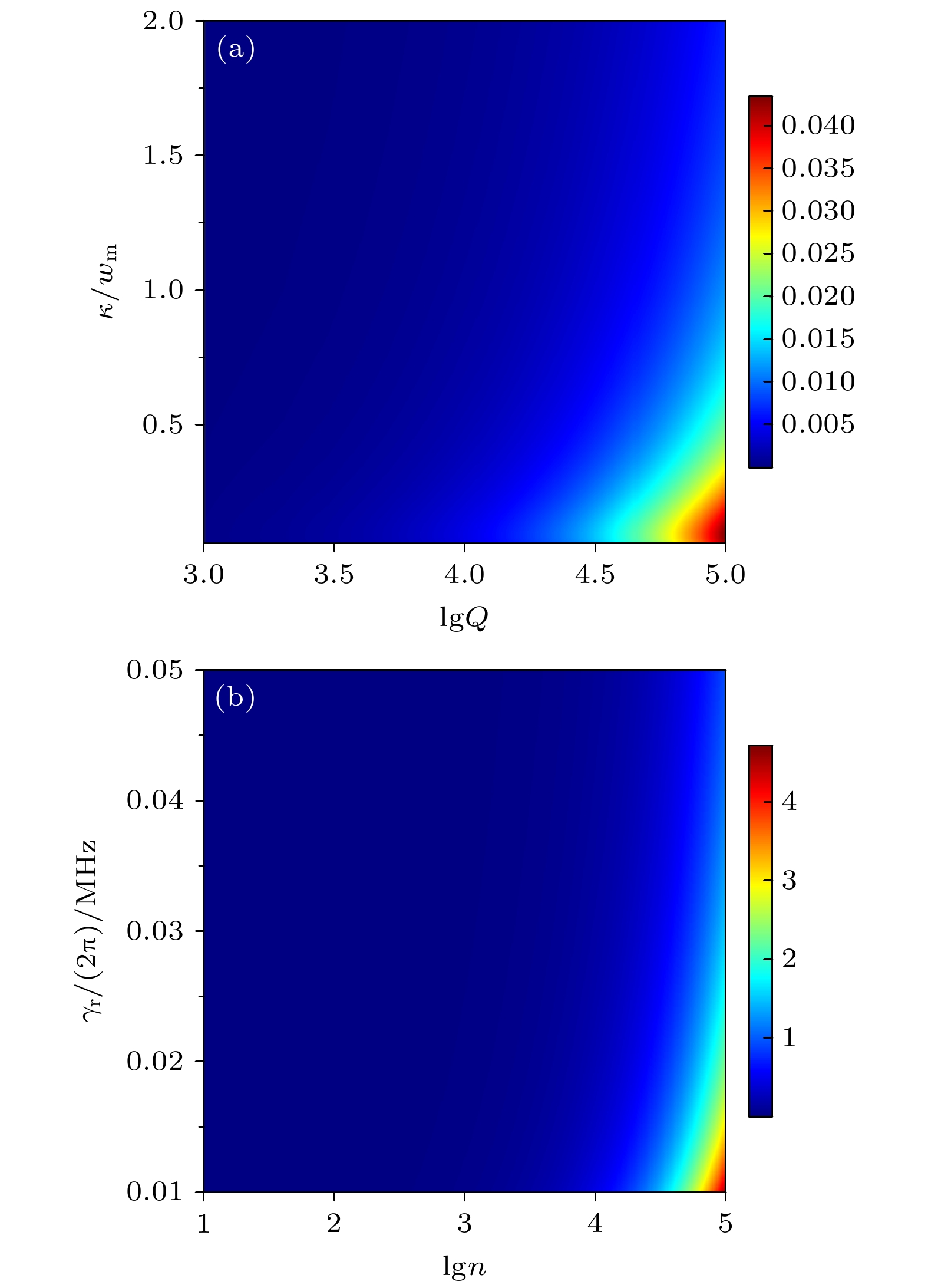
$ {\tau _{\max }} $ 作为$ \kappa /{\omega _{\text{m}}} $ 和lgQ的函数, 其中$ n = {10^4} $ ; (b)$ {\tau _{\max }} $ 作为$ {\gamma _{\text{r}}} $ /(2π)和lgn的函数, 其中$ \kappa /{\omega _{\text{m}}} = 0.1 $ . 其他参数同图2Fig. 6. (a)
$ {\tau _{\max }} $ as a function of$ \kappa /{\omega _{\text{m}}} $ and lgQ, where$ n = $ $ {10^4} $ ; (b)$ {\tau _{\max }} $ as a function of$ {\gamma _{\text{r}}} $ /(2π) and lgn, while$ \kappa /{\omega _{\text{m}}} = $ $ 0.1 $ . Other parameters are the same as those in Fig. 2. -
[1] Kippenberg T J, Vahala K J 2008 Science 321 1172
Google Scholar
[2] Aspelmeyer M, Gröblacher S, Hammerer K 2010 J. Opt. Soc. Am. B 27 A189
Google Scholar
[3] Aspelmeyer M, Meystre P, Schwab K 2012 Phys. Today 65 29
[4] Xiong H, Si L G, Zheng A S 2012 Phys. Rev. A 86 013815
Google Scholar
[5] Lü X Y, Wu Y, Johansson J R, Jing H, Zhang J, Nori F 2015 Phys. Rev. Lett. 114 253601
Google Scholar
[6] Lü X Y, Wu Y, Johansson J R, Jing H, Zhang J, Nori F 2015 Phys. Rev. Lett. 114 093602
Google Scholar
[7] Grudinin I S, Lee H, Painter O, Vahala K J 2010 Phys. Rev. Lett. 104 083901
Google Scholar
[8] Mahboob I, Nishiguchi K, Fujiwara A, Yamaguchi H 2013 Phys. Rev. Lett. 110 127202
Google Scholar
[9] Jing H, Özdemir S K, Lü X Y, Zhang J, Yang L, Nori F 2014 Phys. Rev. Lett. 113 053604
Google Scholar
[10] Brooks D W C, Botter T, Schreppler S, Purdy T P, Brahms N, Stamper-Kurn D M 2012 Nature 488 476
Google Scholar
[11] LaHaye M D, Camarota O B B, Schwab K C 2004 Science 304 74
Google Scholar
[12] Ekinci K L, Yang Y T, Roukes M L 2004 J. Appl. Phys. 95 2682
Google Scholar
[13] Caves C M 1980 Phys. Rev. Lett. 45 75
Google Scholar
[14] Gavartin E, Verlot P, Kippenberg T J 2012 Nat. Nanotechnol. 7 509
Google Scholar
[15] Chan J, Mayer Alegre T P, Safavi-Naeini A H, Hill J T, Krause A, Groblacher S, Aspelmeyer M, Painter O 2011 Nature 478 89
Google Scholar
[16] Aspelmeyer M, Kippenberg T J, Marquardt F 2014 Rev. Mod. Phys. 86 1391
Google Scholar
[17] Mancini S, Giovannetti V, Vitali D, Tombesi P 2002 Phys. Rev. Lett. 88 120401
Google Scholar
[18] Harris S E 1997 Phys. Today 50 36
[19] Fleichhauer M, Imamoglu A, Marangos J P 2005 Rev. Mod. Phys. 77 633
Google Scholar
[20] Agarwal G S, Huang S 2010 Phys. Rev. A 81 041803
Google Scholar
[21] Weis S, Rivière R, Deléglise S 2010 Science 330 1520
Google Scholar
[22] Safavi-Naeini A H, Mayer Alegre T P, Chan J, Eichenfield M, Winger M, Lin Q, Hill J T, Chang D E, Painter O 2011 Nature 472 69
Google Scholar
[23] Akram M J, Khan M M, Saif F 2015 Phys. Rev. A 92 023846
Google Scholar
[24] Yan X B 2020 Phys. Rev. A 101 043820
Google Scholar
[25] Ian H, Gong Z R, Liu Y 2008 Phys. Rev. A 78 013824
Google Scholar
[26] Genes C, Vitali D, Tombesi P 2008 Phys. Rev. A 77 050307
Google Scholar
[27] Akram M J, Ghafoor F, Saif F 2015 J. Phys. B At. Mol. Opt. Phys. 48 065502
Google Scholar
[28] Paternostro M, De Chiara G, Palma G M 2010 Phys. Rev. Lett. 104 243602
Google Scholar
[29] Jia W Z, Wang Z D 2013 Phys. Rev. A 88 063821
Google Scholar
[30] Lecocq F, Teufel J D, Aumentado J 2015 Nat. Phys. 11 635
Google Scholar
[31] Yan D, Wang Z H, Ren C N, Gao H, Li Y, Wu J H 2015 Phys. Rev. A 91 023813
Google Scholar
[32] Gallagher T F 1994 Rydberg Atoms (Cambridge: Cambridge University Press)
[33] Lukin M D, Fleischhauer M, Cote R, Duan L M, Jaksch D, Cirac J I, Zoller P 2001 Phys. Rev. Lett. 87 037901
Google Scholar
[34] Heidemann R, Raitzsch U, Bendkowsky V, Butscher B, Low R, Santos L, Pfau T 2007 Phys. Rev. Lett. 99 163601
Google Scholar
[35] Saffman M, Walker T, Molmer K 2010 Rev. Mod. Phys. 82 2313
Google Scholar
[36] Weimer H, Muller M, Lesanovsky I, Zoller P, Buchler H P 2010 Nat. Phys. 6 382
Google Scholar
[37] Saffman M, Walker T G 2002 Phys. Rev. A 66 065403
Google Scholar
[38] Fu C B, Yan X B, Gu K H 2013 Phys. Rev. A 87 053841
Google Scholar
[39] Yan D, Bai W J, Bai J N, Chen L, Han H Y, Wu J H 2022 Photonics 9 242
Google Scholar
[40] Marek T, Grigori E A, Boris A M, Dmitry S P 2020 Phys. Rev. A 101 051601
Google Scholar
[41] Khodas M, Pustilnik M, Kamenev A, Glazman L I 2007 Phys. Rev. Lett. 99 110405
Google Scholar
[42] Karla L, Jean-Sébastien B, Roberta C, Edmond O, Corinna K 2018 Phys. Rev. A 98 033605
Google Scholar
[43] Yan X B 2021 J. Phys. B: At. Mol. Opt. Phys. 54 035401
Google Scholar
[44] Walls D F, Milburn G J 1944 Quantum Optics (Berlin: Springer-Verlag) pp127−141
下载:
计量
- 文章访问数: 4094
- PDF下载量: 119
- 被引次数: 0
