多模光力系统中光力诱导透明引起的慢光效应

谢宝豪; 陈华俊; 孙轶

doi:10.7498/aps.72.20230663

摘要

提出了一种多模光力系统, 该系统由一个光学腔与两个机械振子相互作用, 研究了在不同失谐条件下探测透射谱的行为. 在蓝失谐条件下, 探测光谱经历了光力诱导吸收到参量放大的过程, 并且得到过程中的临界泵浦功率. 在红失谐条件下, 研究系统中的光力诱导透明和法诺共振以及相位色散的变化, 比较不同的光机械耦合强度关系、频率关系和失谐的结果. 数值结果表明, 通过控制两个振动镜的频率关系, 探测光的透射强度曲线经历了从法诺共振到光力诱导透明的一系列变化. 由于探测光的透射窗口伴随着快速的相位色散变化, 会导致群延迟, 进一步讨论由光力诱导透明引起的慢光效应, 提出了可以通过改变腔与泵浦失谐来控制快、慢光的传播; 该系统中的光学延迟可以达到毫秒级. 基于阵列结构的多模光力系统将在减缓和存储光脉冲中有潜在的应用前景.

关键词:

Abstract

Owing to the radiation pressure, the cavity optomechanical system can couple the optical field with the mechanical resonator, so the state of the mechanical resonator can be regulated through the optical field. Conversely, the optical field in the optomechanical system can also be regulated by modulating the mechanical element. Therefore, many interesting optical phenomena, such as Fano resonance, optomechanically induced absorption and amplification, and optomechanically induced transparency, can be generated in a cavity optomechanical system. Especially in transparent windows, both absorption and dispersion properties change strongly, which results in extensive applications such as slow light and optical storage. Because of its ultra-high quality factor, small size, mass production on chip and convenient all-optical control, it provides an ideal platform for realizing slow light engineering. In this work, by solving the Heisenberg equation of motion of a multimode optomechanical system composed of an optical cavity and two mechanical oscillators, and then by using the input-output relationship for the cavity, the intensity of probe transmission can be obtained. Taking the experimental date as realistic parameters, the behaviors of probe transmission in different detuning conditions are presented. By controlling the pump power under blue detuning, the probe transmission undergoes a process of optomechanically induced absorption to parametric amplification, and the critical pump power is obtained. In the case of red detuning, optomechanically induced transparency, Fano resonance and phase dispersion of the system are studied, and the results of different mechanical coupling strengths, frequency relations and detuning are compared. The numerical results show that as the mechanical coupling strength between two mechanical oscillators increases, the splitting distance becomes larger, and a larger coupling strength ratio will result in a larger splitting peak width. By controlling the frequency relationship between the two resonators, the probe transmission spectra undergo a series of transitions from Fano resonance to optomechanically induced transparency. Because the transmission window of the probe light is accompanied by rapid phase dispersion change, it will lead to group delay. The slow light effect caused by optomechanically induced transparency is further discussed, and the propagation of fast and slow light can be controlled by pump-cavity detuning. The optical delay in this system can be in the order of milliseconds. The multimode optomechanical system based on array structure has a potential application prospect in slowing and storing light pulses.

Keywords:

作者及机构信息

安徽理工大学力学与光电物理学院, 淮南　232001

通信作者: 陈华俊, chenphysics@126.com

基金项目: 国家自然科学基金(批准号: 11647001, 11804004)、中国博士后科学基金(批准号: 2020M681973)和安徽省自然科学基金(批准号: 1708085QA11)资助的课题.

Authors and contacts

School of Mechanics and Photoelectric Physics, Anhui University of Science and Technology, Huainan 232001, China

Corresponding author: Chen Hua-Jun, chenphysics@126.com

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 11647001, 11804004), the China Postdoctoral Science Foundation (Grant No. 2020M681973), and the Natural Science Foundation of Anhui Province, China (Grant No. 1708085QA11).

文章全文 : translate this paragraph

参考文献

[1]	Aspelmeyer M, Kippenberg T J, Marquardt F 2014 Rev. Mod. Phys. 86 1391 Google Scholar
[2]	Metcalfe M 2014 Appl. Phys. Rev. 1 031105 Google Scholar
[3]	Chan J, Alegre T P M, Safavi-Naeini A H, Hill J T, Krause A, Gröblacher S, Aspelmeyer M, Painter O 2011 Nature 478 89 Google Scholar
[4]	Lai D G, Zou F, Hou B P, Xiao Y F, Liao J Q 2018 Phys. Rev. A 98 023860 Google Scholar
[5]	Alegre T P, Perahia R, Painter O 2010 Opt. Express 18 7872 Google Scholar
[6]	Bagheri M, Poot M, Li M, Pernice W P H, Tang H X 2011 Nat. Nanotechnol. 6 726 Google Scholar
[7]	Cole G D, Aspelmeyer M 2011 Nat. Nanotechnol. 6 690 Google Scholar
[8]	Caulfield H J, Dolev S 2010 Nat. Photonics 4 261 Google Scholar
[9]	Chen H J 2021 Appl. Phys. Express 14 082005 Google Scholar
[10]	Li B B, Ou L, Lei Y, Liu Y C 2021 Nanophotonics 10 2799 Google Scholar
[11]	Li J J, Zhu K D 2012 Appl. Phys. Lett. 101 141905 Google Scholar
[12]	Chen B, Xing H W, Chen J B, Xue H B, Xing L L 2021 Quantum Inf. Process. 20 10 Google Scholar
[13]	Chen H J 2021 Phys. Rev. A 104 013708 Google Scholar
[14]	Chen H J 2022 Results Phys. 42 105987 Google Scholar
[15]	Chen H J 2023 Opt. Laser Technol. 161 109242 Google Scholar
[16]	Agarwal G S, Huang S 2012 Phys. Rev. A 85 021801 Google Scholar
[17]	Mukherjee K, Jana P C 2019 Eur. Phys. J. D 73 264 Google Scholar
[18]	Weis S, Rivière R, Deléglise S, Gavartin E, Arcizet O, Schliesser A, Kippenberg T J 2010 Science 330 1520 Google Scholar
[19]	Xiong H, Wu Y 2018 App. Phys. Rev. 5 031305 Google Scholar
[20]	Lü H, Jiang Y, Wang Y Z, Jing H 2017 Photonics Res. 5 367 Google Scholar
[21]	张利巍, 李贤丽, 杨柳 2019 68 170701 Google Scholar Zhang L W, Li X L, Yang L 2019 Acta Phys. Sin. 68 170701 Google Scholar
[22]	Chen H J, Wu H W, Yang J Y, Li X C, Sun Y J, Peng Y 2019 Nanoscale Res. Lett. 14 73 Google Scholar
[23]	Chen H J, Yang J Y, Zhao D M, Wu H W 2019 Appl. Opt. 58 2463 Google Scholar
[24]	Mahajan S, Singh M K, Bhattacherjee A B 2022 Opt. Quantum Electron. 54 835 Google Scholar
[25]	Liu L W, Gengzang D J, Shi Y Q, Chen Q, Wang X L, Wang P Y 2019 Acta Phys. Pol. A 136 444 Google Scholar
[26]	Xing H W, Chen B, Xing L L, Chen J B, Xue H B, Guo K X 2021 Commun. Theor. Phys. 73 055101 Google Scholar
[27]	Chen B, Shang L, Wang X F, Chen J B, Xue H B, Liu X, Zhang J 2019 Phys. Rev. A 99 063810 Google Scholar
[28]	Wang L D, Yan J K, Zhu X F, Chen B 2017 Physica E 89 134 Google Scholar
[29]	Liu Z X, Xiong H, Wu Y 2018 Phys. Rev. A 97 013801 Google Scholar
[30]	Fano U 1961 Phys. Rev. 124 1866 Google Scholar
[31]	Miroshnichenko A E, Flach S, Kivshar Y S 2010 Rev. Mod. Phys. 82 2257 Google Scholar
[32]	Long X, Zhang M, Xie Z, Tang M, Li L 2020 Opt. Commun. 459 124942 Google Scholar
[33]	Zhen B, Chua S L, Lee J, Rodriguez A W, Liang X, Johnson S G, Joannopoulos J D, Soljačić M, Shapira O 2013 Proc. Natl. Acad. Sci. U. S. A. 110 13711 Google Scholar
[34]	Chen H J 2021 Results Phys. 31 105002 Google Scholar
[35]	Liu Y C, Li B B, Xiao Y F 2017 Nanophotonics 6 789 Google Scholar
[36]	Teufel J D, Li D, Allman M S, Cicak K, Sirois A J, Whittaker J D, Simmonds R W 2011 Nature 471 204 Google Scholar
[37]	Karuza M, Biancofiore C, Bawaj M, Molinelli C, Galassi M, Natali R, Tombesi P, Giuseppe G D, Vitali D 2013 Phys. Rev. A 88 013804 Google Scholar
[38]	Bhattacharya M, Meystre P 2008 Phys. Rev. A 78 041801 Google Scholar
[39]	Jiang C, Cui Y, Bian X, Zuo F, Yu H, Chen G 2016 Phys. Rev. A 94 023837 Google Scholar
[40]	Spethmann N, Kohler J, Schreppler S, Buchmann L, Stamper-Kurn D M 2015 Nat. Phys. 12 27 Google Scholar
[41]	Ullah K, Jing H, Saif F 2018 Phys. Rev. A 97 033812 Google Scholar
[42]	Hill J T, Safavi-Naeini A H, Chan J, Painter O 2012 Nat. Commun. 3 1196 Google Scholar
[43]	Liu Y, Davanco M, Aksyuk V, Srinivasan K 2013 Phys. Rev. Lett. 110 223603 Google Scholar
[44]	Shkarin A B, Flowers-Jacobs N E, Hoch S W, Kashkanova A D, Deutsch C, Reichel J, Harris J G E 2014 Phys. Rev. Lett 112 013602 Google Scholar
[45]	Huang S 2014 J. Phys. B:At. Mol. Opt. Phys. 47 055504 Google Scholar
[46]	Ma P C, Zhang J Q, Xiao Y, Feng M, Zhang Z M 2014 Phys. Rev. A 90 043825 Google Scholar
[47]	Huang J, Lai D G, Liao J Q 2022 Phys. Rev. A 106 063506 Google Scholar
[48]	Lai D G, Liao J Q, Miranowicz A, Nori F 2022 Phys. Rev. Lett. 129 063602 Google Scholar
[49]	Lai D G, Qin W, Hou B P, Miranowicz A, Nori F 2021 Phys. Rev. A 104 043521 Google Scholar
[50]	Mari A, Farace A, Didier N, Giovannetti V, Fazio R 2013 Phys. Rev. Lett. 111 103605 Google Scholar
[51]	Chen H J, Zhao D M, Wu H W, Xu H F 2019 AIP Adv. 9 075105 Google Scholar
[52]	Yang G, Huang Y X, Rao S 2022 Quantum Inf. Process. 22 29 Google Scholar
[53]	Lai D G, Huang J F, Yin X L, Hou B P, Li W, Vitali D, Nori F, Liao J Q 2020 Phys. Rev. A 102 011502 Google Scholar
[54]	Lai D G, Huang J, Hou B P, Nori F, Liao J Q 2021 Phys. Rev. A 103 063509 Google Scholar
[55]	Lai D G, Qin W, Miranowicz A, Nori F 2022 Phys. Rev. Res. 4 033102 Google Scholar
[56]	Huang J, Lai D G, Liu C, Huang J F, Nori F, Liao J Q 2022 Phys. Rev. A 106 013526 Google Scholar
[57]	Ockeloen-Korppi C F, Gely M F, Damskägg E, Jenkins M, Steele G A, Sillanpää M A 2019 Phys. Rev. A 99 023826 Google Scholar
[58]	陈华俊 2020 69 134203 Google Scholar Chen H J 2020 Acta Phys. Sin. 69 134203 Google Scholar
[59]	Ghobadi R, Bahrampour A R, Simon C 2011 Phys. Rev. A 84 033846 Google Scholar
[60]	Jiang C, Chen B, Zhu K D 2011 Europhys. Lett. 94 38002 Google Scholar
[61]	Boller K J, Imamoğlu A, Harris S E 1991 Phys. Rev. Lett. 66 2593 Google Scholar
[62]	Teufel J D, Donner T, Li D, Harlow J W, Allman M S, Cicak K, Sirois A J, Whittaker J D, Lehnert K W, Simmonds R W 2011 Nature 475 359 Google Scholar
[63]	Notomi M, Kuramochi E, Tanabe T 2008 Nat. Photonics 2 741 Google Scholar
[64]	Lai D G, Wang X, Qin W, Hou B P, Nori F, Liao J Q 2020 Phys. Rev. A 102 023707 Google Scholar
[65]	Wu B, Hulbert J F, Lunt E J, Hurd K, Hawkins A R, Schmidt H 2010 Nat. Photonics 4 776 Google Scholar
[66]	Fiore V, Yang Y, Kuzyk M C, Barbour R, Tian L, Wang H 2011 Phys. Rev. Lett. 107 133601 Google Scholar
[67]	Safavi-Naeini A H, Alegre T P M, Chan J, Eichenfield M, Winger M, Lin Q, Hill J T, Chang D E, Painter O 2011 Nature 472 69 Google Scholar
[68]	Chen B, Jiang C, Zhu K D 2011 Phys. Rev. A 83 055803 Google Scholar

施引文献

图 1 多模光力系统示意图, 其中该系统由一束频率为${\omega _{\text{p}}}$泵浦光和一束频率为${\omega _{\text{s}}}$弱探测光同时驱动.

Fig. 1. Schematic diagram of multimode optomechanical system driven by a strong pump filed ${\omega _{\text{p}}}$ and a weak probe field ${\omega _{\text{s}}}$.

下载: 全尺寸图片幻灯片

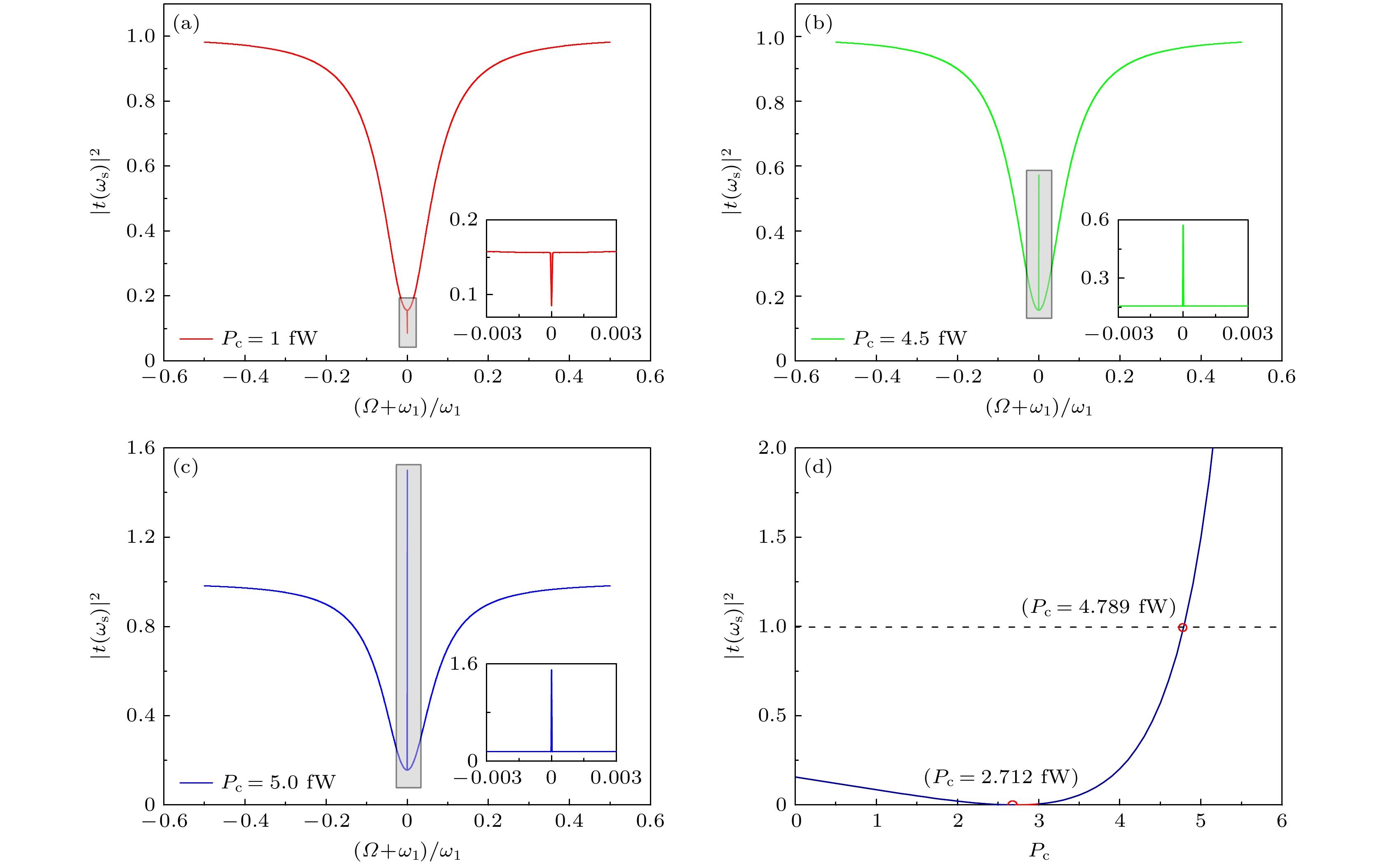
图 2 在失谐$\varDelta=-{\omega _1}$时, 对于不同泵浦光${P_{\text{c}}}$功率下探测场的透射强度${\left| {t({\omega _{\text{s}}})} \right|^2}$作为归一化失谐$(\varOmega + {\omega _1})/{\omega _1}$的函数　(a) ${P_{\text{c}}} = $$ 1{\text{ fW}}$; (b) ${P_{\text{c}}} = 4.5{\text{ fW}}$; (c) ${P_{\text{c}}} = 5{\text{ fW}}$. (d) 探测场的透射强度${\left| {t({\omega _{\text{s}}})} \right|^2}$作为泵浦功率${P_{\text{c}}}$的函数

Fig. 2. (a)−(c) Transmission rate ${\left| {t({\omega _{\text{s}}})} \right|^2}$ of the probe field as a function of normalized detuning $(\varOmega + {\omega _1})/{\omega _1}$ for different pump light power at $\varDelta =-{\omega _1}$: (a) ${P_{\text{c}}} = 1{\text{ fW}}$; (b) ${P_{\text{c}}} = 4.5{\text{ fW}}$; (c) ${P_{\text{c}}} = 5{\text{ fW}}$. (d) Transmission rate ${\left| {t({\omega _{\text{s}}})} \right|^2}$ of the probe field as a function of pump light power.

下载: 全尺寸图片幻灯片

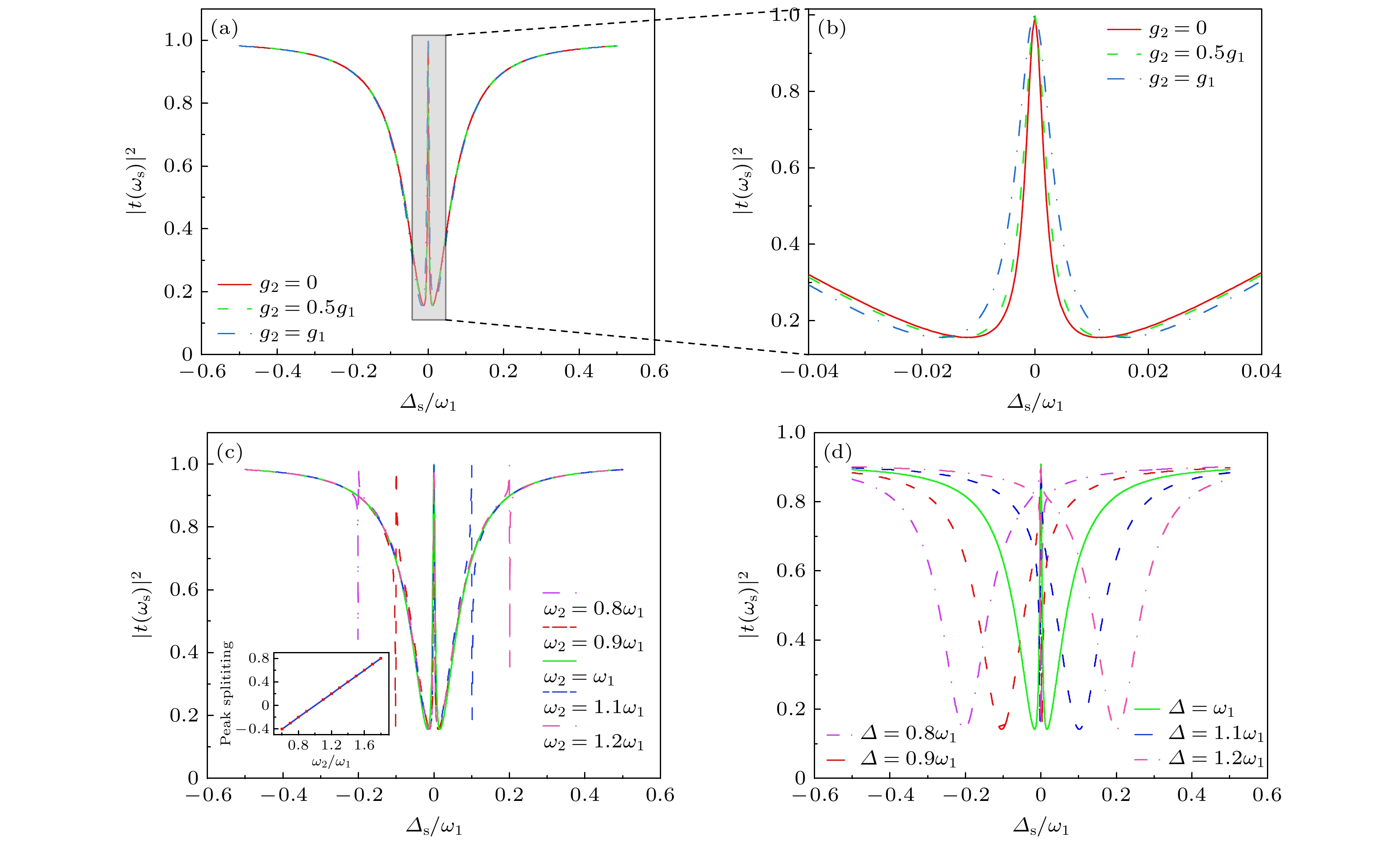
图 3 (a) 在失谐$\varDelta ={\omega _1}$条件下, 光机械耦合强度不同时探测场的透射强度${\left| {t({\omega _{\text{s}}})} \right|^2}$作为探测-腔失谐$ {\varDelta _{\text{s}}}/{\omega _1} $的函数; (b) 图(a)的部分放大图; (c) 在失谐$\varDelta={\omega _1}$条件下, 振子频率不同时探测场的透射强度${\left| {t({\omega _{\text{s}}})} \right|^2}$作为探测-腔失谐${\varDelta _{\text{s}}}/{\omega _1}$的函数; (d) 腔-泵浦失谐不同时, 探测场的透射强度${\left| {t({\omega _{\text{s}}})} \right|^2}$作为探测-腔失谐${\varDelta _{\text{s}}}/{\omega _1}$的函数

Fig. 3. (a) Probe transmission ${\left| {t({\omega _{\text{s}}})} \right|^2}$ as a function of ${\varDelta _{\text{s}}}/{\omega _1}$ for different optomechanical coupling strengths on the condition of $\varDelta={\omega _1}$; (b) the amplification of panel (a); (c) the probe transmission ${\left| {t({\omega _{\text{s}}})} \right|^2}$ as a function of ${\varDelta _{\text{s}}}/{\omega _1}$ for different frequencies of resonators in the condition of $\varDelta={\omega _1}$; (d) the probe transmission ${\left| {t({\omega _{\text{s}}})} \right|^2}$ as a function of ${\varDelta _{\text{s}}}/{\omega _1}$ for different cavity-pump detuning.

下载: 全尺寸图片幻灯片

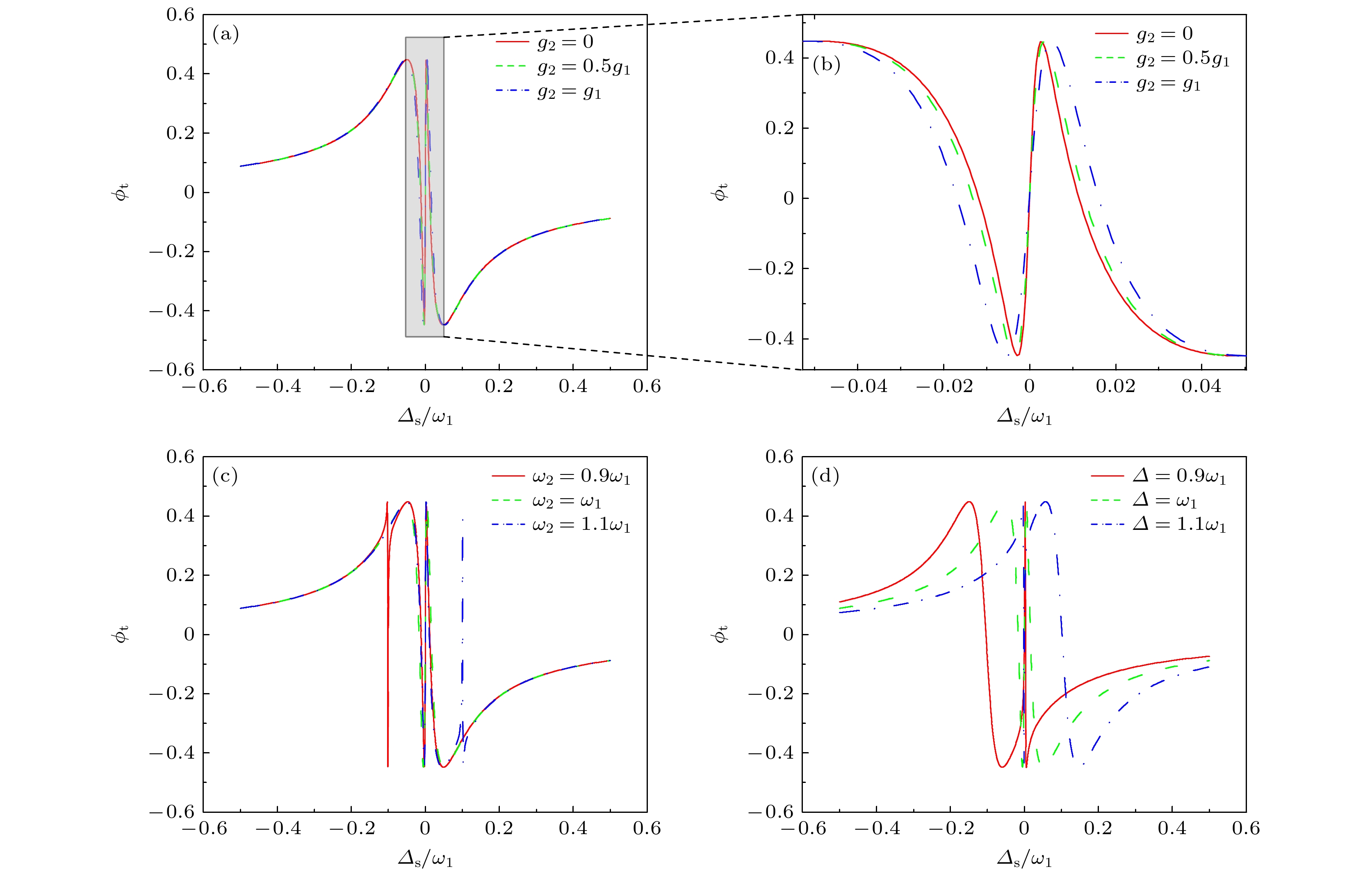
图 4 (a) 在不同光机械耦合强度下, 相位${\phi _{\text{t}}}$作为探测-腔失谐${\varDelta _{\text{s}}}/{\omega _1}$的函数; (b) 图(a)的部分放大图; (c) 在不同振子频率下, 相位${\phi _{\text{t}}}$作为探测-腔失谐${\varDelta _{\text{s}}}/{\omega _1}$的函数; (d) 在不同腔-泵浦失谐下, 相位${\phi _{\text{t}}}$作为探测-腔失谐${\varDelta _{\text{s}}}/{\omega _1}$的函数

Fig. 4. (a) Phase ${\phi _{\text{t}}}$ as a function of ${\varDelta _{\text{s}}}/{\omega _1}$ for different optomechanical coupling strengths; (b) the amplification of panel (a); (c) the phase ${\phi _{\text{t}}}$ as a function of ${\varDelta _{\text{s}}}/{\omega _1}$ for different frequencies of resonators; (d) the phase ${\phi _{\text{t}}}$ as a function of ${\varDelta _{\text{s}}}/{\omega _1}$ for different cavity-pump detuning.

下载: 全尺寸图片幻灯片

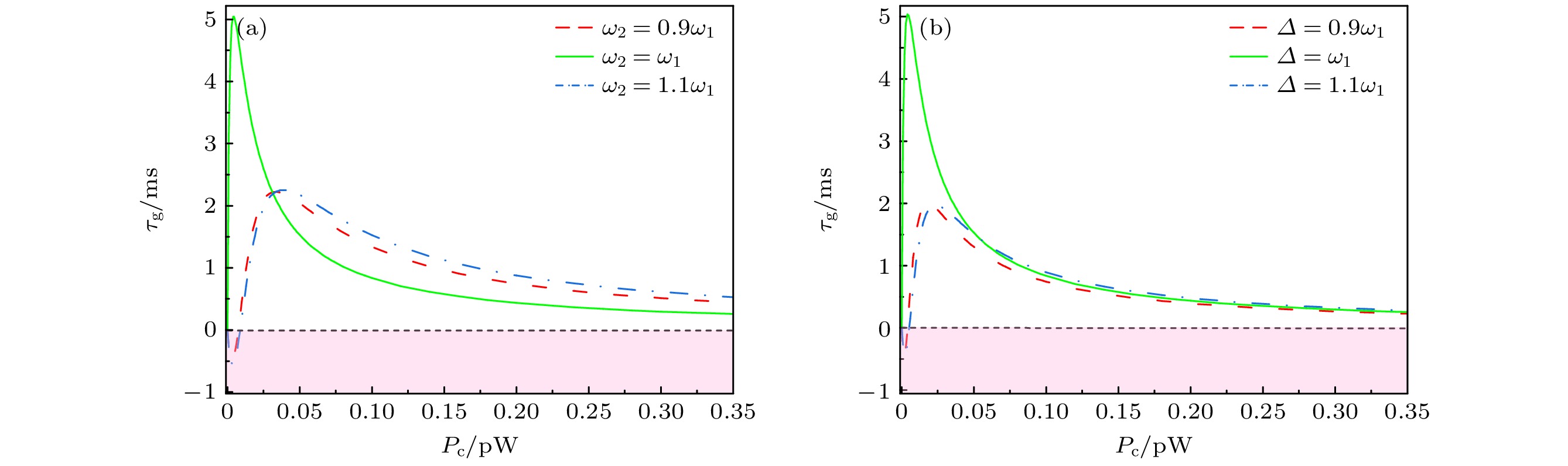
图 5 (a) 不同频率下, 群延迟${\tau _{\text{g}}}$作为泵浦功率${P_{\text{c}}}$的函数; (b) 不同腔-泵失谐下, 群延迟${\tau _{\text{g}}}$作为泵浦功率${P_{\text{c}}}$的函数

Fig. 5. (a) Group delay ${\tau _{\text{g}}}$ as a function of ${P_{\text{c}}}$ for different frequencies of resonators; (b) the group delay ${\tau _{\text{g}}}$ as a function of ${P_{\text{c}}}$ for different cavity-pump detuning.

下载: 全尺寸图片幻灯片

map

[1]	Aspelmeyer M, Kippenberg T J, Marquardt F 2014 Rev. Mod. Phys. 86 1391 Google Scholar
[2]	Metcalfe M 2014 Appl. Phys. Rev. 1 031105 Google Scholar
[3]	Chan J, Alegre T P M, Safavi-Naeini A H, Hill J T, Krause A, Gröblacher S, Aspelmeyer M, Painter O 2011 Nature 478 89 Google Scholar
[4]	Lai D G, Zou F, Hou B P, Xiao Y F, Liao J Q 2018 Phys. Rev. A 98 023860 Google Scholar
[5]	Alegre T P, Perahia R, Painter O 2010 Opt. Express 18 7872 Google Scholar
[6]	Bagheri M, Poot M, Li M, Pernice W P H, Tang H X 2011 Nat. Nanotechnol. 6 726 Google Scholar
[7]	Cole G D, Aspelmeyer M 2011 Nat. Nanotechnol. 6 690 Google Scholar
[8]	Caulfield H J, Dolev S 2010 Nat. Photonics 4 261 Google Scholar
[9]	Chen H J 2021 Appl. Phys. Express 14 082005 Google Scholar
[10]	Li B B, Ou L, Lei Y, Liu Y C 2021 Nanophotonics 10 2799 Google Scholar
[11]	Li J J, Zhu K D 2012 Appl. Phys. Lett. 101 141905 Google Scholar
[12]	Chen B, Xing H W, Chen J B, Xue H B, Xing L L 2021 Quantum Inf. Process. 20 10 Google Scholar
[13]	Chen H J 2021 Phys. Rev. A 104 013708 Google Scholar
[14]	Chen H J 2022 Results Phys. 42 105987 Google Scholar
[15]	Chen H J 2023 Opt. Laser Technol. 161 109242 Google Scholar
[16]	Agarwal G S, Huang S 2012 Phys. Rev. A 85 021801 Google Scholar
[17]	Mukherjee K, Jana P C 2019 Eur. Phys. J. D 73 264 Google Scholar
[18]	Weis S, Rivière R, Deléglise S, Gavartin E, Arcizet O, Schliesser A, Kippenberg T J 2010 Science 330 1520 Google Scholar
[19]	Xiong H, Wu Y 2018 App. Phys. Rev. 5 031305 Google Scholar
[20]	Lü H, Jiang Y, Wang Y Z, Jing H 2017 Photonics Res. 5 367 Google Scholar
[21]	张利巍, 李贤丽, 杨柳 2019 68 170701 Google Scholar Zhang L W, Li X L, Yang L 2019 Acta Phys. Sin. 68 170701 Google Scholar
[22]	Chen H J, Wu H W, Yang J Y, Li X C, Sun Y J, Peng Y 2019 Nanoscale Res. Lett. 14 73 Google Scholar
[23]	Chen H J, Yang J Y, Zhao D M, Wu H W 2019 Appl. Opt. 58 2463 Google Scholar
[24]	Mahajan S, Singh M K, Bhattacherjee A B 2022 Opt. Quantum Electron. 54 835 Google Scholar
[25]	Liu L W, Gengzang D J, Shi Y Q, Chen Q, Wang X L, Wang P Y 2019 Acta Phys. Pol. A 136 444 Google Scholar
[26]	Xing H W, Chen B, Xing L L, Chen J B, Xue H B, Guo K X 2021 Commun. Theor. Phys. 73 055101 Google Scholar
[27]	Chen B, Shang L, Wang X F, Chen J B, Xue H B, Liu X, Zhang J 2019 Phys. Rev. A 99 063810 Google Scholar
[28]	Wang L D, Yan J K, Zhu X F, Chen B 2017 Physica E 89 134 Google Scholar
[29]	Liu Z X, Xiong H, Wu Y 2018 Phys. Rev. A 97 013801 Google Scholar
[30]	Fano U 1961 Phys. Rev. 124 1866 Google Scholar
[31]	Miroshnichenko A E, Flach S, Kivshar Y S 2010 Rev. Mod. Phys. 82 2257 Google Scholar
[32]	Long X, Zhang M, Xie Z, Tang M, Li L 2020 Opt. Commun. 459 124942 Google Scholar
[33]	Zhen B, Chua S L, Lee J, Rodriguez A W, Liang X, Johnson S G, Joannopoulos J D, Soljačić M, Shapira O 2013 Proc. Natl. Acad. Sci. U. S. A. 110 13711 Google Scholar
[34]	Chen H J 2021 Results Phys. 31 105002 Google Scholar
[35]	Liu Y C, Li B B, Xiao Y F 2017 Nanophotonics 6 789 Google Scholar
[36]	Teufel J D, Li D, Allman M S, Cicak K, Sirois A J, Whittaker J D, Simmonds R W 2011 Nature 471 204 Google Scholar
[37]	Karuza M, Biancofiore C, Bawaj M, Molinelli C, Galassi M, Natali R, Tombesi P, Giuseppe G D, Vitali D 2013 Phys. Rev. A 88 013804 Google Scholar
[38]	Bhattacharya M, Meystre P 2008 Phys. Rev. A 78 041801 Google Scholar
[39]	Jiang C, Cui Y, Bian X, Zuo F, Yu H, Chen G 2016 Phys. Rev. A 94 023837 Google Scholar
[40]	Spethmann N, Kohler J, Schreppler S, Buchmann L, Stamper-Kurn D M 2015 Nat. Phys. 12 27 Google Scholar
[41]	Ullah K, Jing H, Saif F 2018 Phys. Rev. A 97 033812 Google Scholar
[42]	Hill J T, Safavi-Naeini A H, Chan J, Painter O 2012 Nat. Commun. 3 1196 Google Scholar
[43]	Liu Y, Davanco M, Aksyuk V, Srinivasan K 2013 Phys. Rev. Lett. 110 223603 Google Scholar
[44]	Shkarin A B, Flowers-Jacobs N E, Hoch S W, Kashkanova A D, Deutsch C, Reichel J, Harris J G E 2014 Phys. Rev. Lett 112 013602 Google Scholar
[45]	Huang S 2014 J. Phys. B:At. Mol. Opt. Phys. 47 055504 Google Scholar
[46]	Ma P C, Zhang J Q, Xiao Y, Feng M, Zhang Z M 2014 Phys. Rev. A 90 043825 Google Scholar
[47]	Huang J, Lai D G, Liao J Q 2022 Phys. Rev. A 106 063506 Google Scholar
[48]	Lai D G, Liao J Q, Miranowicz A, Nori F 2022 Phys. Rev. Lett. 129 063602 Google Scholar
[49]	Lai D G, Qin W, Hou B P, Miranowicz A, Nori F 2021 Phys. Rev. A 104 043521 Google Scholar
[50]	Mari A, Farace A, Didier N, Giovannetti V, Fazio R 2013 Phys. Rev. Lett. 111 103605 Google Scholar
[51]	Chen H J, Zhao D M, Wu H W, Xu H F 2019 AIP Adv. 9 075105 Google Scholar
[52]	Yang G, Huang Y X, Rao S 2022 Quantum Inf. Process. 22 29 Google Scholar
[53]	Lai D G, Huang J F, Yin X L, Hou B P, Li W, Vitali D, Nori F, Liao J Q 2020 Phys. Rev. A 102 011502 Google Scholar
[54]	Lai D G, Huang J, Hou B P, Nori F, Liao J Q 2021 Phys. Rev. A 103 063509 Google Scholar
[55]	Lai D G, Qin W, Miranowicz A, Nori F 2022 Phys. Rev. Res. 4 033102 Google Scholar
[56]	Huang J, Lai D G, Liu C, Huang J F, Nori F, Liao J Q 2022 Phys. Rev. A 106 013526 Google Scholar
[57]	Ockeloen-Korppi C F, Gely M F, Damskägg E, Jenkins M, Steele G A, Sillanpää M A 2019 Phys. Rev. A 99 023826 Google Scholar
[58]	陈华俊 2020 69 134203 Google Scholar Chen H J 2020 Acta Phys. Sin. 69 134203 Google Scholar
[59]	Ghobadi R, Bahrampour A R, Simon C 2011 Phys. Rev. A 84 033846 Google Scholar
[60]	Jiang C, Chen B, Zhu K D 2011 Europhys. Lett. 94 38002 Google Scholar
[61]	Boller K J, Imamoğlu A, Harris S E 1991 Phys. Rev. Lett. 66 2593 Google Scholar
[62]	Teufel J D, Donner T, Li D, Harlow J W, Allman M S, Cicak K, Sirois A J, Whittaker J D, Lehnert K W, Simmonds R W 2011 Nature 475 359 Google Scholar
[63]	Notomi M, Kuramochi E, Tanabe T 2008 Nat. Photonics 2 741 Google Scholar
[64]	Lai D G, Wang X, Qin W, Hou B P, Nori F, Liao J Q 2020 Phys. Rev. A 102 023707 Google Scholar
[65]	Wu B, Hulbert J F, Lunt E J, Hurd K, Hawkins A R, Schmidt H 2010 Nat. Photonics 4 776 Google Scholar
[66]	Fiore V, Yang Y, Kuzyk M C, Barbour R, Tian L, Wang H 2011 Phys. Rev. Lett. 107 133601 Google Scholar
[67]	Safavi-Naeini A H, Alegre T P M, Chan J, Eichenfield M, Winger M, Lin Q, Hill J T, Chang D E, Painter O 2011 Nature 472 69 Google Scholar
[68]	Chen B, Jiang C, Zhu K D 2011 Phys. Rev. A 83 055803 Google Scholar

[1]	王鑫, 任飞帆, 韩嵩, 韩海燕, 严冬. 里德伯原子辅助光力系统的完美光力诱导透明及慢光效应. , 2023, 72(9): 094203. doi: 10.7498/aps.72.20222264
[2]	孙占硕, 王鑫, 王俊林, 樊勃, 张宇, 冯瑶. 基于类电磁诱导透明的双频段太赫兹超材料的传感和慢光特性. , 2022, 71(13): 138101. doi: 10.7498/aps.71.20212163
[3]	赵嘉栋, 张好, 杨文广, 赵婧华, 景明勇, 张临杰. 基于里德伯原子电磁诱导透明效应的光脉冲减速. , 2021, 70(10): 103201. doi: 10.7498/aps.70.20210102
[4]	李森, 李浩珍, 许静平, 朱成杰, 羊亚平. 基于腔光力学系统的全光三极管的压缩特性. , 2019, 68(17): 174202. doi: 10.7498/aps.68.20190078
[5]	谷开慧, 严冬, 张孟龙, 殷景志, 付长宝. 原子辅助光力系统中快慢光的量子调控. , 2019, 68(5): 054201. doi: 10.7498/aps.68.20181424
[6]	张利巍, 李贤丽, 杨柳. 蓝失谐驱动下双腔光力系统中的光学非互易性. , 2019, 68(17): 170701. doi: 10.7498/aps.68.20190205
[7]	潘庭婷, 曹文, 邓彩松, 王鸣, 夏巍, 郝辉. X-两环结构的光学特性研究. , 2018, 67(15): 157301. doi: 10.7498/aps.67.20172582
[8]	张秀龙, 鲍倩倩, 杨明珠, 田雪松. 双腔光力学系统中输出光场纠缠特性的研究. , 2018, 67(10): 104203. doi: 10.7498/aps.67.20172467
[9]	邓瑞婕, 闫智辉, 贾晓军. 基于电磁诱导透明机制的压缩光场量子存储. , 2017, 66(7): 074201. doi: 10.7498/aps.66.074201
[10]	王维, 高社生, 孟阳. 型谐振腔结构的光学透射特性. , 2017, 66(1): 017301. doi: 10.7498/aps.66.017301
[11]	陈华俊, 方贤文, 陈昌兆, 李洋. 基于双回音壁模式腔光力学系统的光学传播特性和超高分辨率光学质量传感. , 2016, 65(19): 194205. doi: 10.7498/aps.65.194205
[12]	陈雪, 刘晓威, 张可烨, 袁春华, 张卫平. 腔光力学系统中的量子测量. , 2015, 64(16): 164211. doi: 10.7498/aps.64.164211
[13]	沈云, 傅继武, 于国萍. 增益对一维周期结构慢光传输特性影响. , 2014, 63(17): 174202. doi: 10.7498/aps.63.174202
[14]	严晓波, 杨柳, 田雪冬, 刘一谋, 张岩. 参量放大器腔中光力诱导透明与本征模劈裂性质. , 2014, 63(20): 204201. doi: 10.7498/aps.63.204201
[15]	付静, 刘万芳, 赵玉杰. 电磁诱导光透明过程中的Wigner-Yanse偏振信息. , 2013, 62(17): 170302. doi: 10.7498/aps.62.170302
[16]	罗松, 付统, 张中月. 内嵌银纳米棒圆形银缝隙结构中的法诺共振现象. , 2013, 62(14): 147303. doi: 10.7498/aps.62.147303
[17]	马雅男, 罗斌, 潘炜, 闫连山, 邹喜华, 易安林, 叶佳, 温坤华, 郑狄. 垂直腔面发射激光器的饱和效应对慢光延时影响的研究. , 2012, 61(1): 014215. doi: 10.7498/aps.61.014215
[18]	鲁辉, 田慧平, 李长红, 纪越峰. 基于二维光子晶体耦合腔波导的新型慢光结构研究. , 2009, 58(3): 2049-2055. doi: 10.7498/aps.58.2049
[19]	姚鸣, 朱卡的, 袁晓忠, 蒋逸文, 吴卓杰. 声子辅助的电磁感应透明和超慢光效应的研究. , 2006, 55(4): 1769-1773. doi: 10.7498/aps.55.1769
[20]	邓诚先, 李正佳, 朱长虹. 具有腔内光放大的单共振光参量振荡器. , 2005, 54(10): 4754-4760. doi: 10.7498/aps.54.4754

计量

文章访问数: 2996
PDF下载量: 85
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

多模光力系统中光力诱导透明引起的慢光效应