-
全光二极管和全光三极管是实现全光逻辑器件的基础. 我们之前已经研究了基于腔量子电动力学的全光二极管的量子统计性质[
1 ], 讨论了在相干光和压缩光入射的情况下, 通过二极管后输出光的压缩性质. 这里将研究拓展到全光三极管, 以基于腔光机械系统的全光三极管作为研究对象. 这种全光三极管通过改变经典抽运光的强度可以对探测光的输出进行有效调控, 并可实现光放大. 本文具体讨论以压缩光以及相干光作为探测光, 通过全光三极管后其输出光的压缩特性. 研究结果表明, 当探测光为相干光时, 不论是否工作在光放大区域, 输出光依然为相干光, 没有被压缩. 而当输入探测光为压缩光时, 在全光三极管的光放大区域, 输出光依然是压缩光, 但压缩特性受到输入光压缩特性以及系统参数的调制. 当输入探测压缩光的压缩角为0时, 输出光的压缩参量S1的最小值随输入探测光压缩系数r的增大而减小, 最小值接近压缩极限–0.25. 但当输入探测压缩光的压缩角改变时, 其对输出光的压缩参量S1,2影响很大, 压缩性会消失. 只有当压缩角θ为π的整数倍时, 输出光的压缩性最好. 这一结果在量子测量、弱信号检测等领域有着潜在的应用价值.All-optical diodes and all-optical transistors are the basis of all-optical logic devices. We study the quantum statistical properties of all-optical diodes based on cavity quantum electrodynamics (QED)[1 ], and discuss the squeezed properties of the output light after passing through the diode when coherent light and squeezed light are incident. Here we extend our research to all-optical transistor, and take all-optical transistor based on cavity optomechanical system as the research object. By changing the intensity of classical pump light, the all-optical transistor can effectively control the output of the probe light and realize optical amplification. We discuss the squeezed properties of the output light of the all-optical transistor with squeezed light and coherent light as the probe light. Our results show that when the probe light is coherent, the output light remains coherent no matter whether it works in the amplified region, and is not squeezed. When the input probe light is amplitude squeezed light, the output light is still squeezed light in the light amplification region of all-optical transistor, but the squeezed properties are modulated by the input light squeezed properties and system parameters. When the squeezed angle of the input probe squeezed light is 0°, the minimum squeezed parameter S1 of the output squeezed light decreases with the increase of the squeezed coefficient r of the input probe light, and the minimum value approaches to the squeezed limit of –0.25. But the change of squeezed angle of the input probe squeezed light changes has a great influence on the squeezed parameter S1,2 of the output light, and the squeezed properties will disappear. Only when the squeezed angle is an integer multiple of π, will the squeezed properties of the output light be best. This result has a potential application value in quantum measurement, weak signal detection, and other fields.-
Keywords:
- all-optical transisitor /
- squeeze light /
- cavity optomechanical system
[1] Li H Z, Xu J P, Wang D W, Xia X W, Yang Y P, Zhu S Y 2017 Phys. Rev. A 96 013832
Google Scholar
[2] Koppens F H L, Buizert C, Tielrooij K J, Vink I T, Nowack K C, Meunier T, ouwenhoven L P K, Vandersypen L M K 2006 Nature 442 766
Google Scholar
[3] Orrit M 2009 Nature 460 42
Google Scholar
[4] Chang D E, Sørensen A S, Demler E A, Lukin M D 2007 Nat. Phys. 3 807
Google Scholar
[5] Hwang J, Pototschnig M, Lettow R, Zumofen G, Renn A, Götzinger S, Sandoghdar V 2009 Nature 460 76
Google Scholar
[6] Li J J, Zhu K D 2011 Nanotechnology 22 055202
Google Scholar
[7] Tominaga J, Mihalcea C, Büchel D, Fukuda H, Nakano T, Atoda N 2001 Appl. Phys. Lett 78 2417
Google Scholar
[8] Hong F Y, Xiong S J 2008 Phys. Rev. A 78 013812
Google Scholar
[9] Hong F Y, Xiong S J 2008 Nanoscale. Res. Lett. 3 361
Google Scholar
[10] Dawes A M C 2009 Phys. Status. Solidi R 3 A17
Google Scholar
[11] Gröblacher S, Hammerer K, Vanner M R, Aspelmeyer M 2009 Nature 460 724
Google Scholar
[12] Genes C, Vitali D, Tombesi P, Gigan S, Aspelmeyer M 2008 Phys. Rev. A 77 033804
Google Scholar
[13] Wilson-Rae I, Nooshi N, Zwerger W, Kippenberg T J 2007 Phys. Rev. Lett. 99 093901
Google Scholar
[14] Agarwal G S, Huang S 2010 Phys. Rev. A 81 041803
Google Scholar
[15] Thompson J D, Zwickl B M, Jayich A M, Marquardt F, Girvin S M, Harris J G E 2008 Nature 452 72
Google Scholar
[16] Sankey J C, Yang C, Zwickl B M, Jayich A M, Harris J G E 2010 Nat. Phys. 6 707
Google Scholar
[17] Zhao Y, Wilson D J, Ni K K, Kimble H J 2012 Opt. Express 20 3586
Google Scholar
[18] Biancofiore C, Karuza M, Galassi M, Natali R, Tombesi P, Giuseppe G D, Vitali D 2011 Phys. Rev. A 84 033814
Google Scholar
[19] Weis S, Rivière R, Deléglise S, Gavartin E, Arcizet O, Schliesser A, Kippenberg T J 2010 Science 330 1520
Google Scholar
[20] Teufel J D, Li D, Allman M S, Cicak K, Sirois A J, Whittaker J D, Simmonds R W 2011 Nature 471 204
Google Scholar
[21] Safavi-Naeini A H, Alegre T P M, Chan J, Eichenfield M, Winger M, Lin Q, Hill J T, Chang D E, Painter O 2011 Nature 472 69
Google Scholar
[22] Nunnenkamp A, Børkje K, Girvin S M 2011 Phys. Rev. Lett. 107 063602
Google Scholar
[23] Marquardt F, Girvin S M 2009 Physics 2 40
Google Scholar
[24] Larson J, Horsdal M 2011 Phys. Rev. A 84 021804
Google Scholar
[25] Chen B, Jiang C, Li J J, Zhu K D 2011 Phys. Rev. A 84 055802
Google Scholar
[26] 彭堃墀 1991 物理 20 588
Google Scholar
Peng K C 1991 Physics 20 588
Google Scholar
[27] Brennecke F, Ritter S, Donner T, Esslinger T 2008 Science 322 235
Google Scholar
[28] Brennecke F, Donner T, Ritter S, Bourde T, Köh M, Esslinger T 2007 Nature 450 268
Google Scholar
[29] Masse F, Heikkilä T T, Pirkkalainen J M, Cho S U, Saloniemi H, Hakonen P J, Sillanpää M A 2011 Nature 480 351
Google Scholar
[30] 张岩, 于旭东, 邸克, 李卫, 张靖 2013 62 084204
Google Scholar
Zhang Y, Yu X D, Di K, Li W, Zhang J 2013 Acta Phys. Sin. 62 084204
Google Scholar
-
图 2 透射率
$ T={|{C}_{{{\rm o}{\rm u}{\rm t}}^{+}}/{E}_{{\rm p}{\rm r}}|}^{2}$ 在不同的抽运光功率下, 随探测光与腔模的频率失谐量$ {\varDelta }{'}_{{\rm p}{\rm r}{\rm c}}={\omega }_{{\rm p}{\rm r}}-{\omega }_{{\rm c}}{'}$ 的变化, 抽运光的频率满足蓝失谐条件$ {\varDelta }_{{\rm c}}=-{\omega }_{m}$ Fig. 2. The relationship between the transmissivity
$ T={|{C}_{{{\rm o}{\rm u}{\rm t}}^{+}}/{E}_{{\rm p}{\rm r}}|}^{2}$ and the frequency detuning of the probe light and the cavity mode ($ {\varDelta }{'}_{{\rm p}{\rm r}{\rm c}}={\omega }_{{\rm p}{\rm r}}-{\omega }_{{\rm c}}{'}$ ) at different pump power. The frequency of the pump light satisfies the condition of blue detuning($ {\varDelta }_{{\rm c}}=-{\omega }_{m}$ ).
图 3 在输入的探测光为压缩光的情况下, 输出光的线性部分的压缩分量
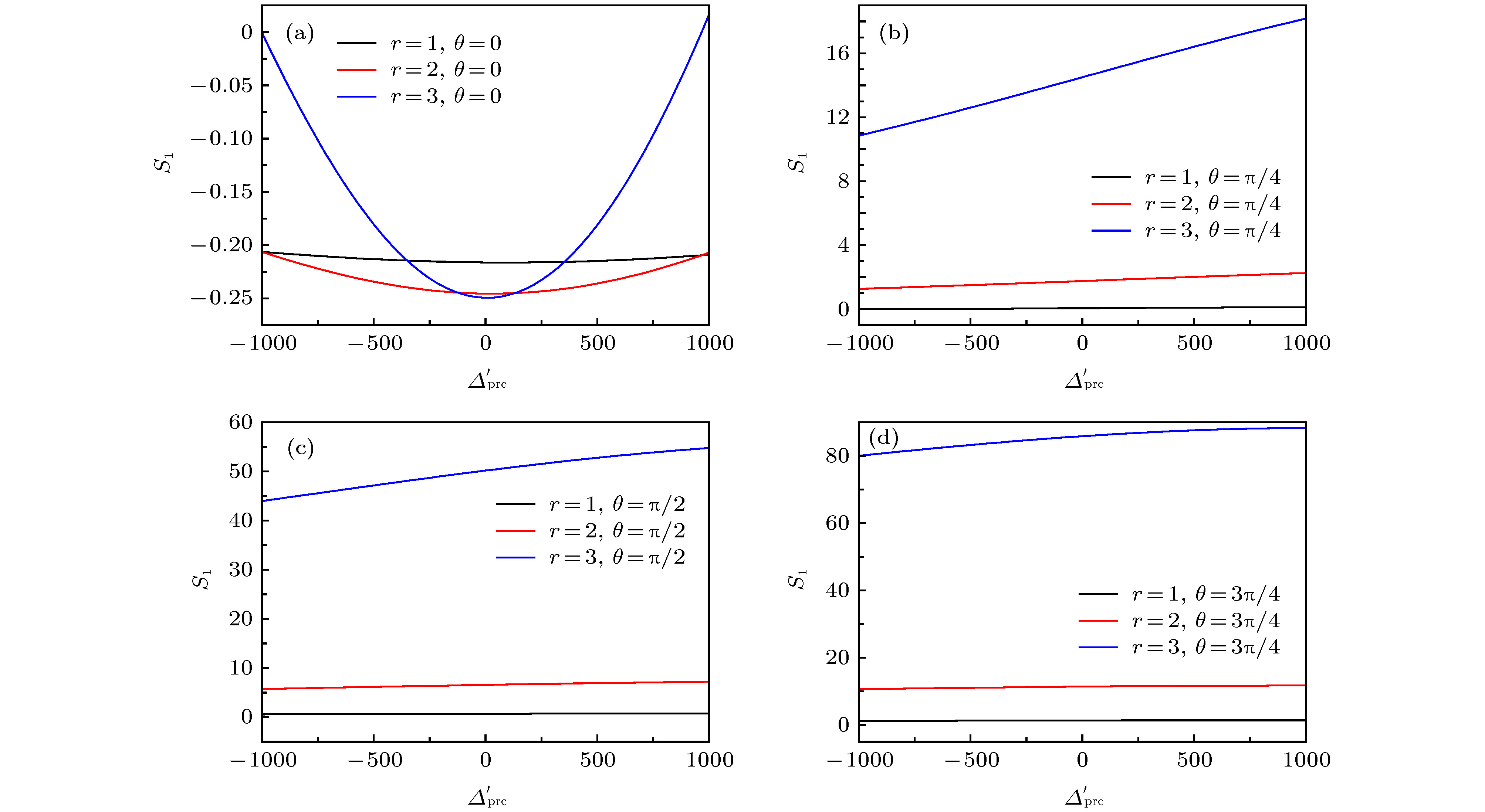
$ {S}_{1}$ 随有效探测-腔失谐量$ {\varDelta }{'}_{{\rm p}{\rm r}{\rm c}}={\omega }_{{\rm p}{\rm r}}-{\omega }_{{\rm c}}{'}$ 的变化, 探测压缩光的压缩角θ为(a) 0, (b) π/4, (c) π/2 (d) 3π/4Fig. 3. When the input probe light is squeeze light, the squeeze component
$ {S}_{1}$ of the linear part of the output light varies with the effective detection-cavity detuning value ($ {\varDelta }{'}_{{\rm p}{\rm r}{\rm c}}={\omega }_{{\rm p}{\rm r}}-{\omega }_{{\rm c}}{'}$ ). The squeeze angle of the probe light is (a) 0, (b) π/4, (c) π/2 (d) 3π/4
图 4 输出光的线性部分的压缩量
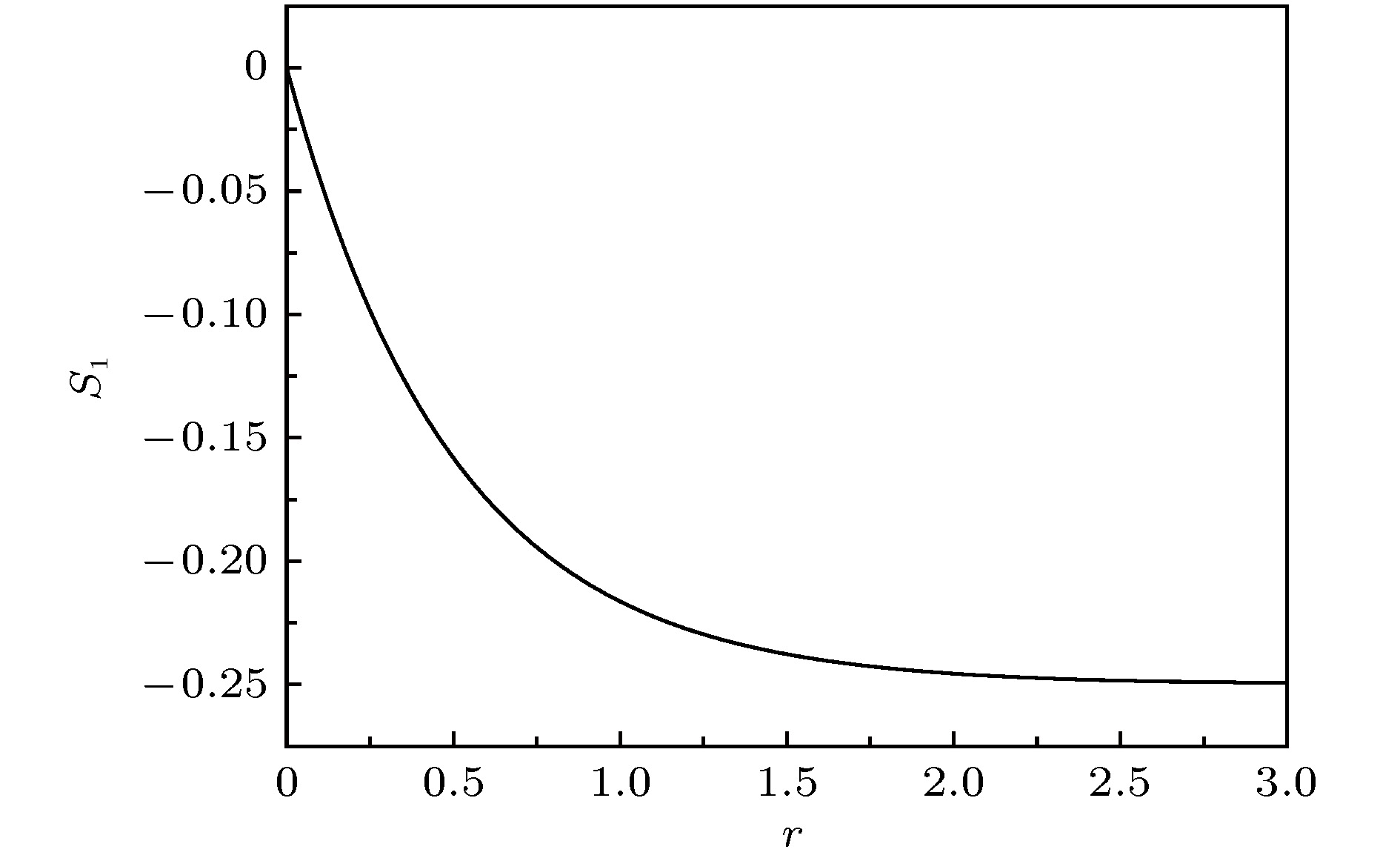
$ {S}_{1}$ 随入射探测光的压缩幅r的变化, 入射探测光的压缩角为θ = 0, 频率与腔模共振$ {\varDelta }{'}_{{\rm p}{\rm r}{\rm c}}=0$ Fig. 4. The variation of the squeeze parameter S1 of the linear part of the output light with the squeeze amplitude r of the incident probe light, the squeeze angle of the incident probe light is θ = 0, and the frequency is resonant with the cavity mode
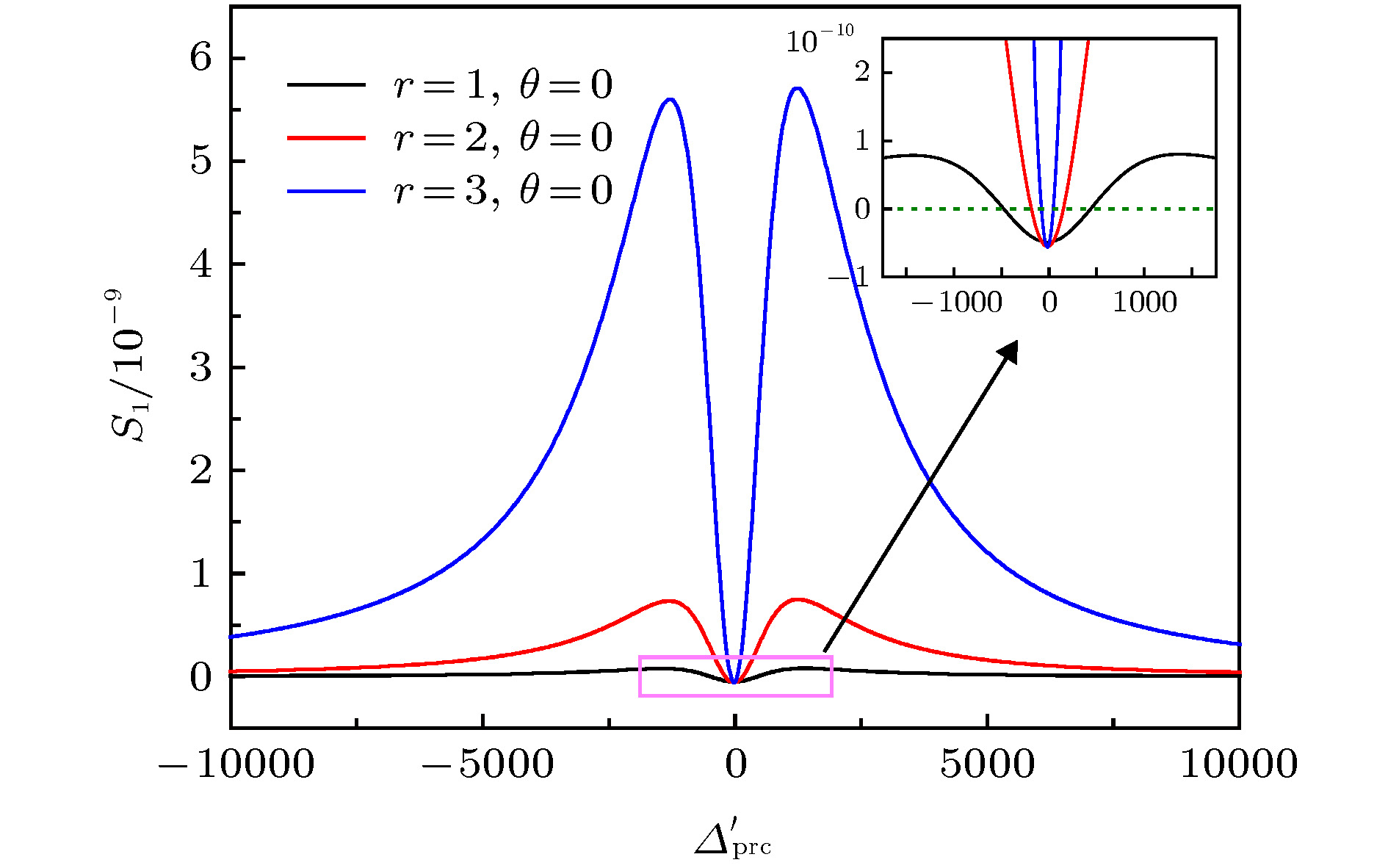
$ {\varDelta }{'}_{{\rm p}{\rm r}{\rm c}}=0$ .
图 5 在不同入射压缩光压缩幅的情况下, 输出光中的非线性部分的压缩量
$ {S}_{1}$ 随入射探测压缩光频率的变化.$ {\varDelta }{'}_{{\rm p}{\rm r}{\rm c}}={\omega }_{{\rm p}{\rm r}}-{\omega }_{{\rm c}}{'}$ 为探测光与腔模的频率失谐Fig. 5. The squeeze parameter S1 of the non-linear part of the output light varies with the frequency of the incident probe squeeze light in the case of different squeeze amplitudes of the incident squeeze light,
$ \varDelta{'} _{\rm{prc}}={{\omega }_{\rm{pr}}}-\omega_{\rm{c}}{'}$ is the frequency detuning between the probe light and the cavity mode. -
[1] Li H Z, Xu J P, Wang D W, Xia X W, Yang Y P, Zhu S Y 2017 Phys. Rev. A 96 013832
Google Scholar
[2] Koppens F H L, Buizert C, Tielrooij K J, Vink I T, Nowack K C, Meunier T, ouwenhoven L P K, Vandersypen L M K 2006 Nature 442 766
Google Scholar
[3] Orrit M 2009 Nature 460 42
Google Scholar
[4] Chang D E, Sørensen A S, Demler E A, Lukin M D 2007 Nat. Phys. 3 807
Google Scholar
[5] Hwang J, Pototschnig M, Lettow R, Zumofen G, Renn A, Götzinger S, Sandoghdar V 2009 Nature 460 76
Google Scholar
[6] Li J J, Zhu K D 2011 Nanotechnology 22 055202
Google Scholar
[7] Tominaga J, Mihalcea C, Büchel D, Fukuda H, Nakano T, Atoda N 2001 Appl. Phys. Lett 78 2417
Google Scholar
[8] Hong F Y, Xiong S J 2008 Phys. Rev. A 78 013812
Google Scholar
[9] Hong F Y, Xiong S J 2008 Nanoscale. Res. Lett. 3 361
Google Scholar
[10] Dawes A M C 2009 Phys. Status. Solidi R 3 A17
Google Scholar
[11] Gröblacher S, Hammerer K, Vanner M R, Aspelmeyer M 2009 Nature 460 724
Google Scholar
[12] Genes C, Vitali D, Tombesi P, Gigan S, Aspelmeyer M 2008 Phys. Rev. A 77 033804
Google Scholar
[13] Wilson-Rae I, Nooshi N, Zwerger W, Kippenberg T J 2007 Phys. Rev. Lett. 99 093901
Google Scholar
[14] Agarwal G S, Huang S 2010 Phys. Rev. A 81 041803
Google Scholar
[15] Thompson J D, Zwickl B M, Jayich A M, Marquardt F, Girvin S M, Harris J G E 2008 Nature 452 72
Google Scholar
[16] Sankey J C, Yang C, Zwickl B M, Jayich A M, Harris J G E 2010 Nat. Phys. 6 707
Google Scholar
[17] Zhao Y, Wilson D J, Ni K K, Kimble H J 2012 Opt. Express 20 3586
Google Scholar
[18] Biancofiore C, Karuza M, Galassi M, Natali R, Tombesi P, Giuseppe G D, Vitali D 2011 Phys. Rev. A 84 033814
Google Scholar
[19] Weis S, Rivière R, Deléglise S, Gavartin E, Arcizet O, Schliesser A, Kippenberg T J 2010 Science 330 1520
Google Scholar
[20] Teufel J D, Li D, Allman M S, Cicak K, Sirois A J, Whittaker J D, Simmonds R W 2011 Nature 471 204
Google Scholar
[21] Safavi-Naeini A H, Alegre T P M, Chan J, Eichenfield M, Winger M, Lin Q, Hill J T, Chang D E, Painter O 2011 Nature 472 69
Google Scholar
[22] Nunnenkamp A, Børkje K, Girvin S M 2011 Phys. Rev. Lett. 107 063602
Google Scholar
[23] Marquardt F, Girvin S M 2009 Physics 2 40
Google Scholar
[24] Larson J, Horsdal M 2011 Phys. Rev. A 84 021804
Google Scholar
[25] Chen B, Jiang C, Li J J, Zhu K D 2011 Phys. Rev. A 84 055802
Google Scholar
[26] 彭堃墀 1991 物理 20 588
Google Scholar
Peng K C 1991 Physics 20 588
Google Scholar
[27] Brennecke F, Ritter S, Donner T, Esslinger T 2008 Science 322 235
Google Scholar
[28] Brennecke F, Donner T, Ritter S, Bourde T, Köh M, Esslinger T 2007 Nature 450 268
Google Scholar
[29] Masse F, Heikkilä T T, Pirkkalainen J M, Cho S U, Saloniemi H, Hakonen P J, Sillanpää M A 2011 Nature 480 351
Google Scholar
[30] 张岩, 于旭东, 邸克, 李卫, 张靖 2013 62 084204
Google Scholar
Zhang Y, Yu X D, Di K, Li W, Zhang J 2013 Acta Phys. Sin. 62 084204
Google Scholar
下载:
计量
- 文章访问数: 7058
- PDF下载量: 75
- 被引次数: 0
